ニューラルネットワーク、多様体、トポロジー

Christopher Olah氏のブログ記事
http://colah.github.io/posts/2014-03-NN-Manifolds-Topology/
の翻訳です。
翻訳の誤りなどあればご指摘お待ちしております。

---

#ニューラルネットワーク、多様体、トポロジー

近年、深層ニューラルネットワークには多くの興奮と関心が寄せられています。コンピュータビジョンなどの分野でブレークスルーとなる成果を達成したためです。¹

しかし、それにはいくつかの懸念が残ります。そのひとつは、ニューラルネットワークが実際に 何を やっているかを理解することが、かなり難問であり得る、ということです。よく訓練されたネットワークは高品質の結果を達成しますが、どのようにしてそうしているかを理解することは困難です。ネットワークが失敗した場合、何がうまくいかなかったかについて理解することは難しいです。

一般的に深層ニューラルネットワークの挙動を理解することは困難ですが、低次元の深層ニューラルネットワーク、すなわち各層ごとにわずかなニューロンのみを持つネットワークを探究する方がはるかに簡単であることが分かりました。実際、このようなネットワークの挙動と訓練を完全に理解するための視覚化をすることができます。この観点から、ニューラルネットワークの挙動についてのより深い直観を獲得し、ニューラルネットワークとトポロジーと呼ばれる数学の分野との関連を観察することができます。

このことから、興味深いいくつかのことが従います。例えば、あるデータセットの分類をするニューラルネットワークの複雑さに対する根源的な下限などです。

##単純な例

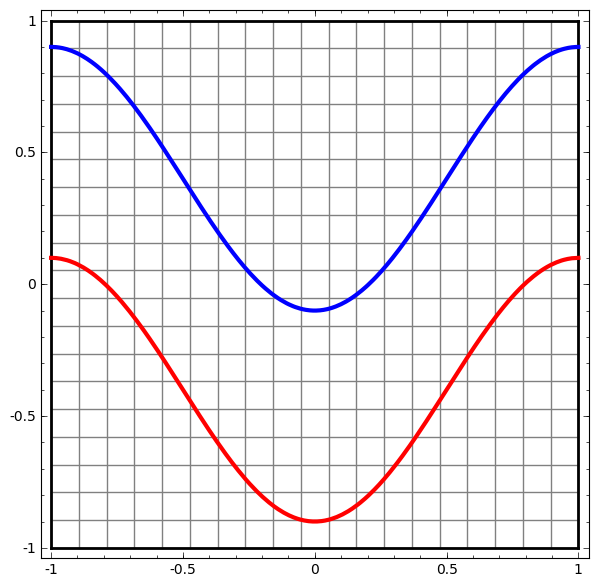
それでは、とても単純なデータセット、平面上の２本の曲線から始めましょう。ネットワークは、点がどちらに属しているか分類することを学習します。

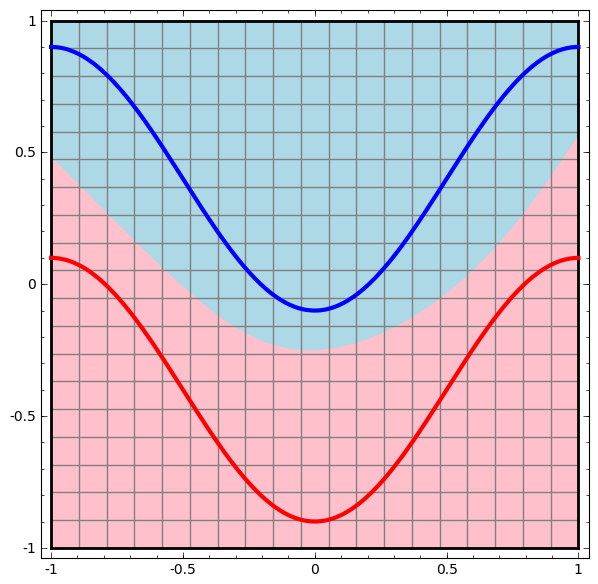
ニューラルネットワーク、あるいは任意の分類アルゴリズムでも、それに関する挙動を可視化する明白な方法は、単にあらゆるデータ・ポイントがどのように分類されるかを見ることです。

最も単純なニューラルネットワークのクラス、１つの入力層と１つの出力層のみを持つものから始めましょう。このようなネットワークは、単に直線で分割することにより、データの２つのクラスを分離することを試みます。

この種のネットワークはあまり面白くありません。一般に、現在のニューラルネットワークは入力と出力の間に「隠れ」層と呼ばれる複数の層を持ちます。少なくとも、１つは持ちます。

単純なネットワークの図（ウィキペディアより）

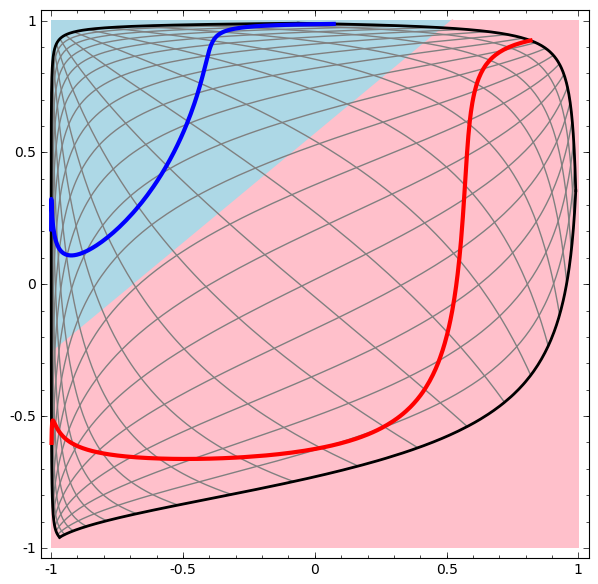
さきほどと同様、領域内のいろいろな点がどうなるかを見ることにより、ネットワークの挙動を可視化することができます。それはデータを直線よりも複雑な曲線により分離します。

各層により、ネットワークは新たな表現を作り、² データを変換します。これらの各表現におけるデータ、および、ネットワークがそのデータを分類する方法を見ることができます。最終的な表現では、ネットワークはデータを貫く直線（または、高次元では、超平面）を描きます。

さきほどの可視化では、データの「生の」表現を見ました。これは入力層を見ていると考えることができます。次に、第１層により変換された後を見ます。これは隠れ層を見ていると考えることができます。

各次元は層内のニューロンの発火に対応しています。

隠れ層はデータが線形分離可能であるような表現を学習

##層の連続的可視化

前節で概説したアプローチで、各層に対応する表現を見ることでネットワークを理解することができるようになりました。これにより表現の離散的なリストが得られます。

扱いにくい部分は、ある表現から別の表現へどのように写るかを理解するところです。ありがたいことに、ニューラルネットワークの層には、これをとても簡単にする素晴らしい性質があります。

ニューラルネットワークで使用される層には、多種多様なものがあります。具体例として、 tanh 層について述べます。 tanh 層 $\tanh(Wx+b)$ は以下により構成されます。

1. 「重み」行列 $W$ による線形変換
2. ベクトル $b$ による並進
3. tanh の各点適用

次のように、連続的な変換としてこれを視覚化することができます：

アフィン変換につづく単調活性化関数の各点適用により構成される、多くの他の標準的な層についても、ストーリーは同様です。

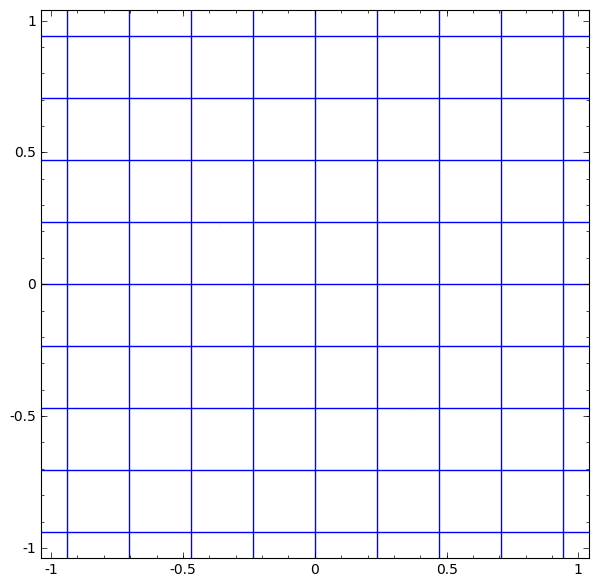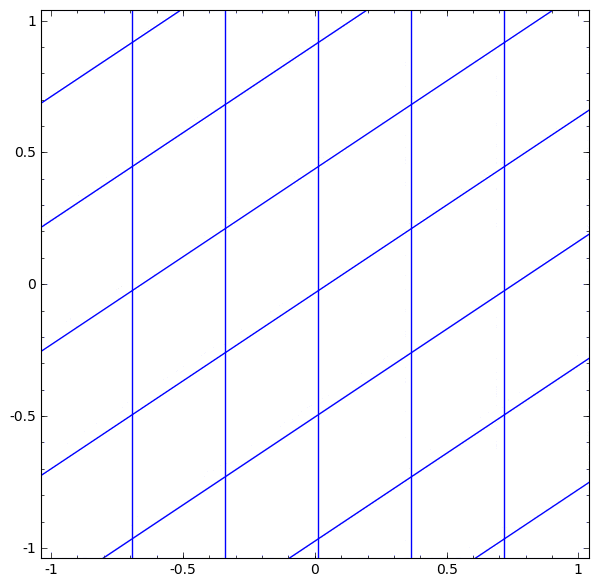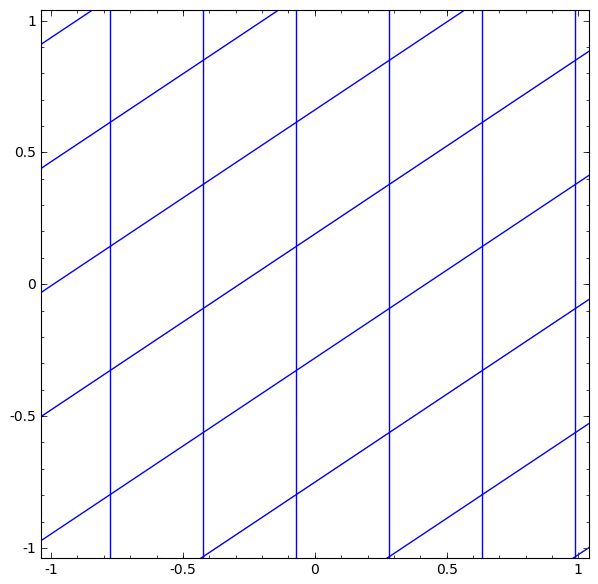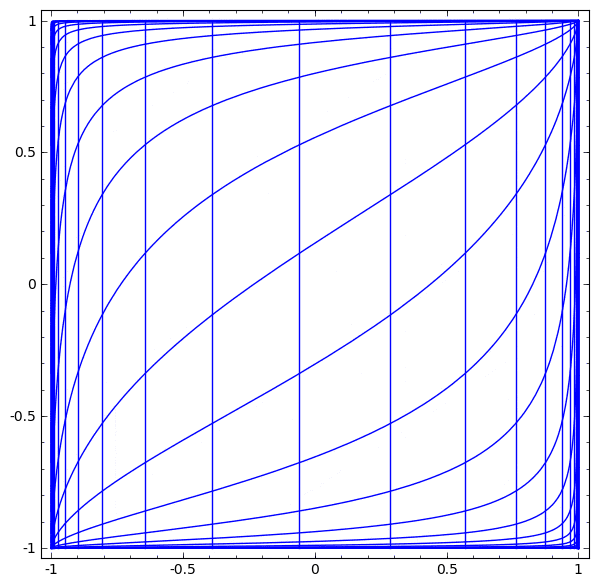
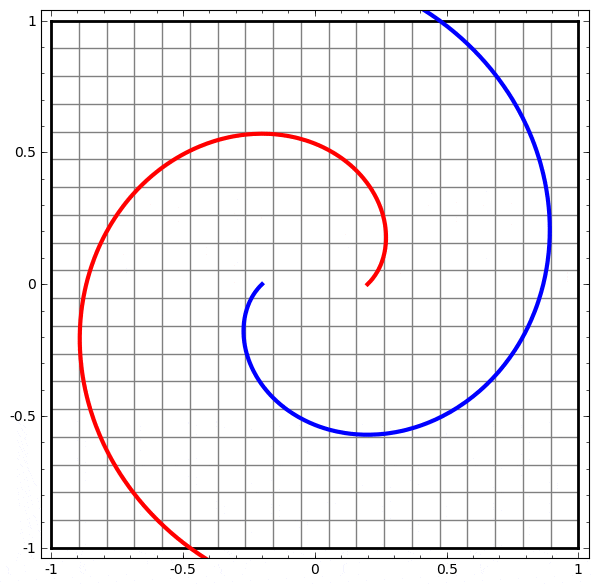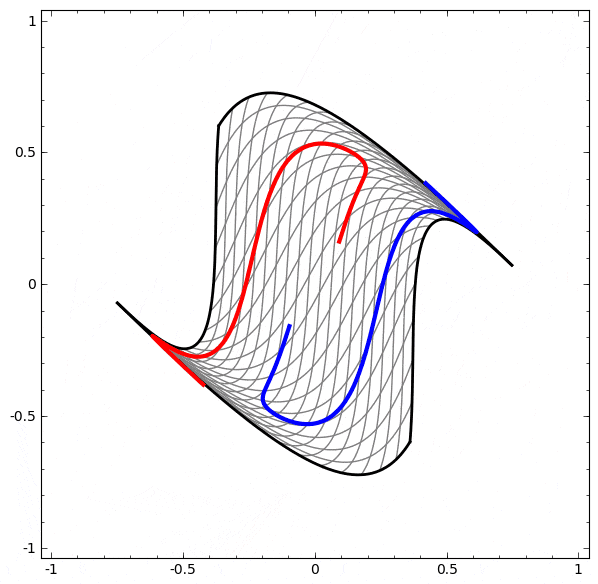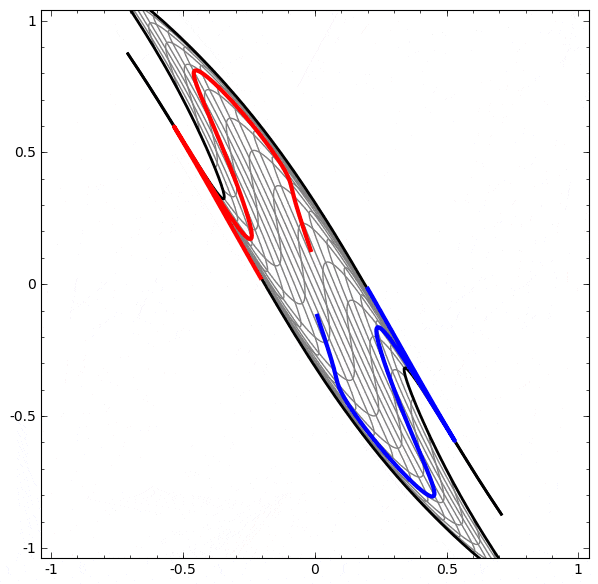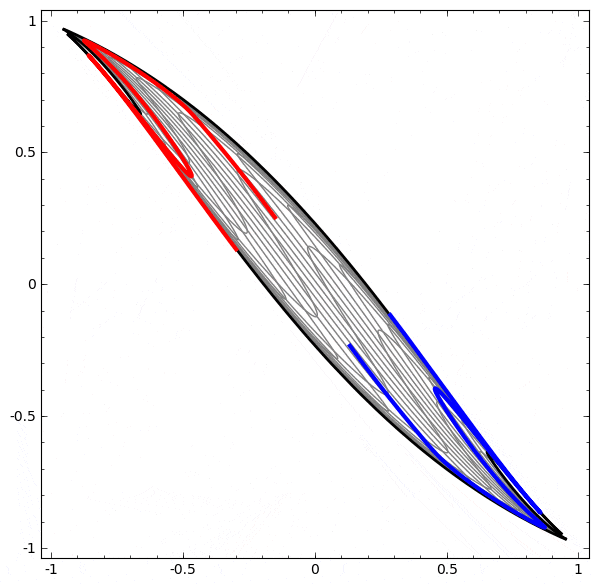
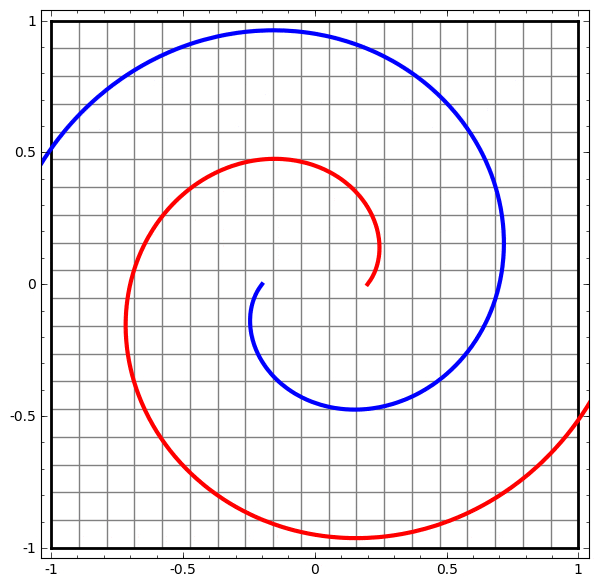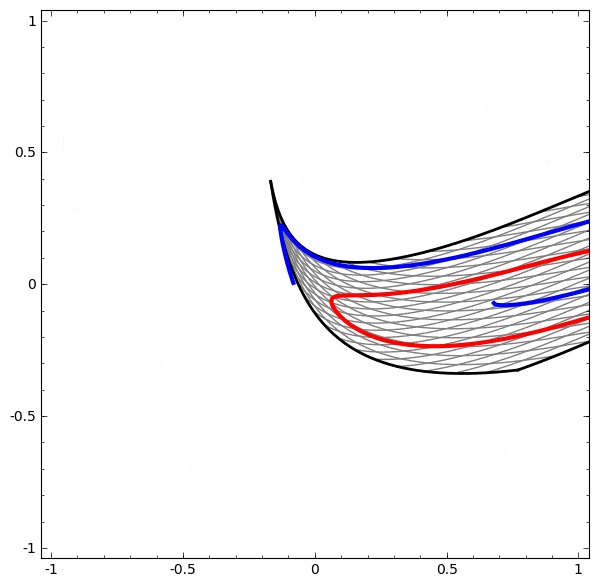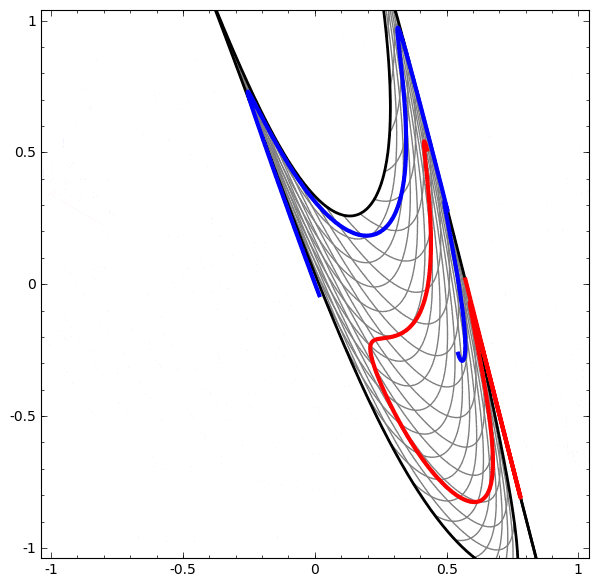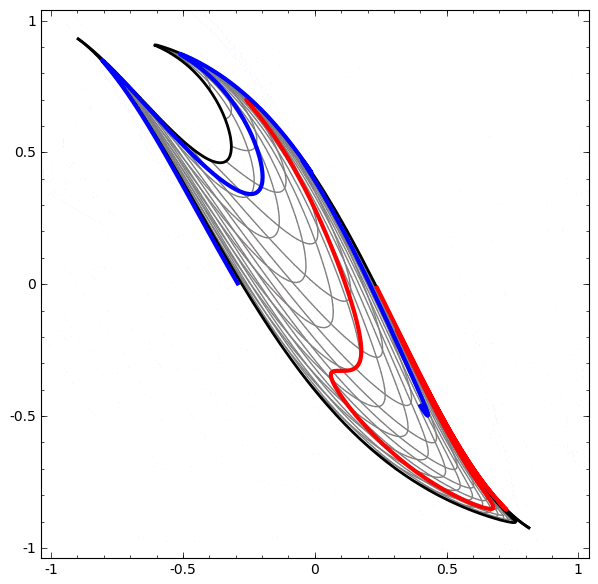
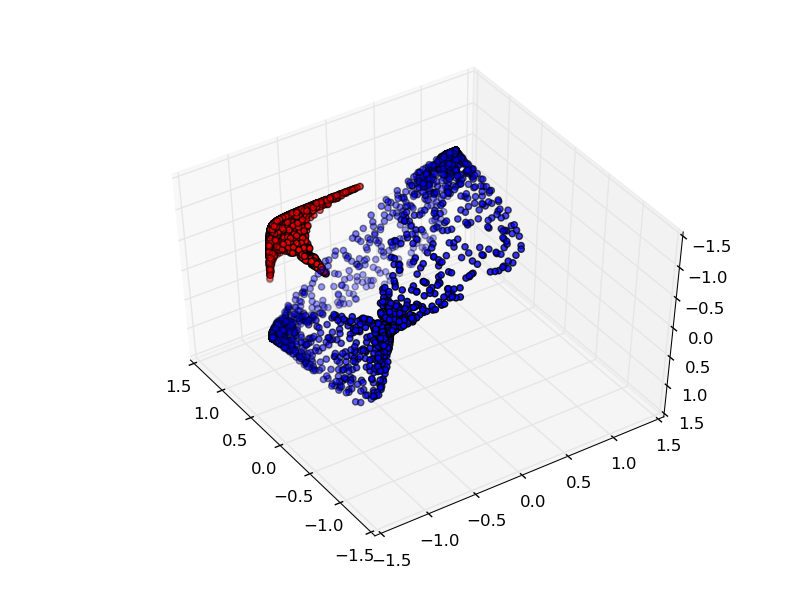
より複雑なネットワークの理解のために、このテクニックを適用することもできます。例えば、以下のネットワークは４つの隠れ層を使用して、わずかに絡み合う２つの螺旋を分類します。時間とともに、「生の」表現からデータを分類するために学習された高レベルな表現にシフトするところを見ることができます。螺旋は、最初は絡み合っていますが、最終的には線形分離可能です。

一方、次のネットワークは、同じく複数の層を使用していますが、より絡み合う２つの螺旋を分類することに失敗しています。

低次元のニューラルネットワークを使用しているためにこのタスクがやや困難であることに、注意してください。より広いネットワークを使用すれば、これはとても簡単でしょう。

（Andrej Karpathyは、この種の訓練の視覚化により対話形式でネットワークを探究することができる、素晴らしいデモをConvnetJSで作りました！）

tanh 層のトポロジー

各層は空間を伸ばしたり、潰したりしますが、切ったり、壊したり、折ったりはしません。直観的に、それが位相的性質を保つことがわかります。例えば、層の前で連結集合であれば、層の後も連結集合です（そしてその逆も）。

このような、位相に影響を与えない変換は、同相写像と呼ばれます。正式には、それらは双方向に連続関数である全単射です。

定理： $N$ 入力 $N$ 出力の層は、重み行列 $W$ が非特異であれば、同相写像である。（ただし定義域と値域に注意する必要がある。）

証明：段階的に考える。

1. $W$ が0でない行列式を持つと仮定する。すると、それは線形な逆を持つ全単射線形関数である。線形関数は連続である。そのため、 $W$ を掛けることは同相である。
2. 並進は同相である。
3. tanhは（シグモイドやソフトプラスもであるが、ReLUはそうではない）連続な逆を持つ連続関数である。定義域と値域を注意深く考慮すれば、それは全単射である。それを各点適用することは同相である。

従って、 $W$ が0でない行列式を持てば、層は同相である。∎

この結果は、このような層を任意の数組み合わせた場合も成り立ちます。

##トポロジーと分類

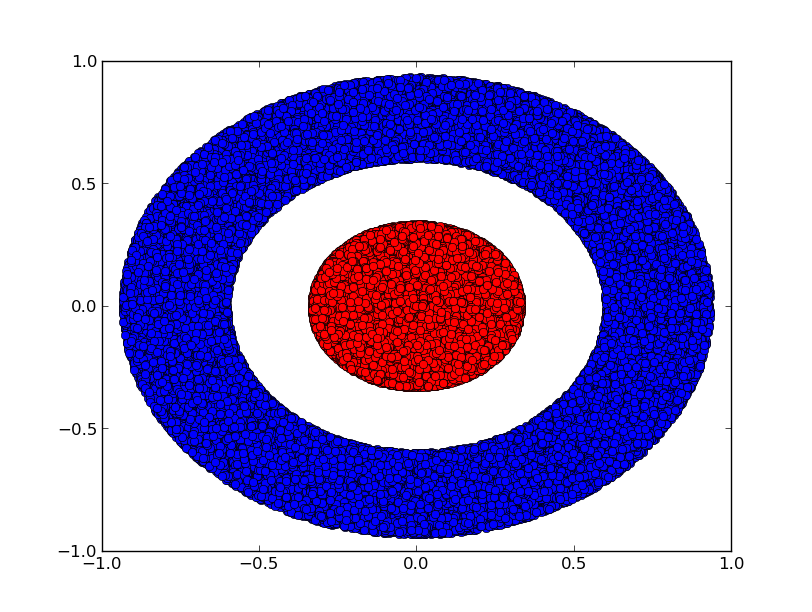
２つのクラス $A, B \subset \mathbb{R}^2$ と２次元のデータセットを考えてみましょう：

A = \{x | d(x,0) < 1/3\}
B = \{x | 2/3 < d(x,0) < 1\}

$A$は赤、$B$は青

主張：深さに関わらず、３つ以上の隠れユニットを持つ層がなければ、ニューラルネットワークでこのデータセットを分類することは不可能である。

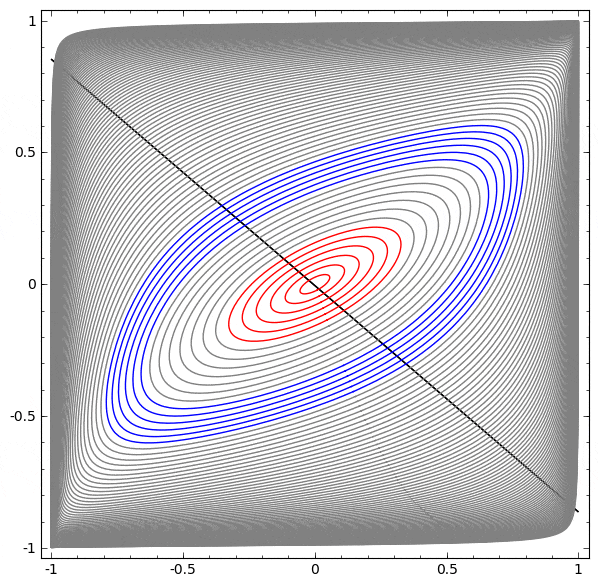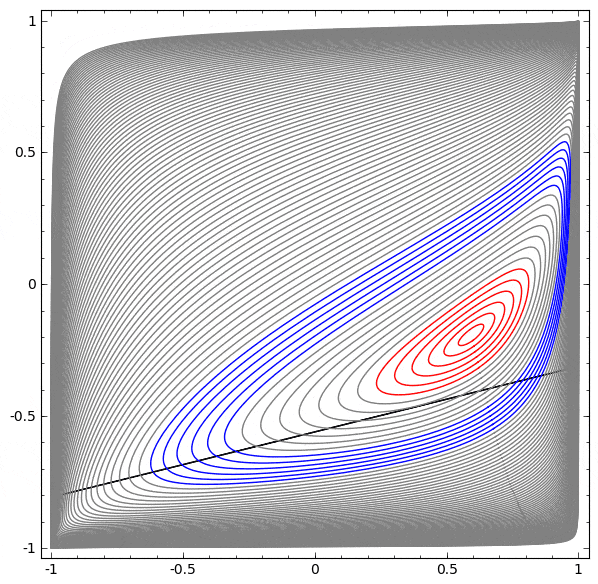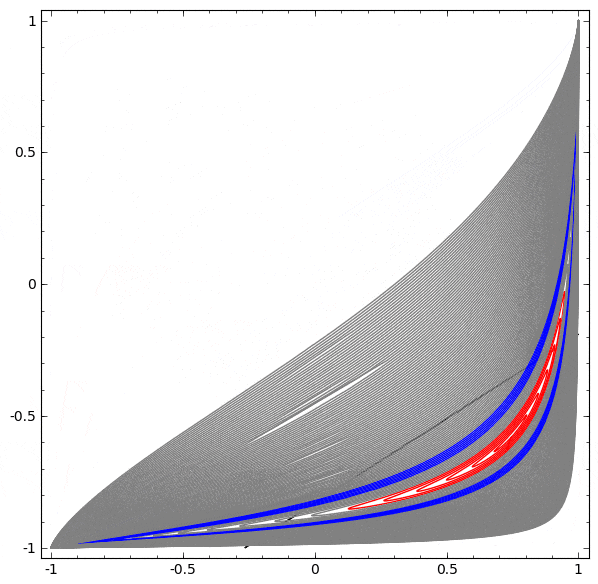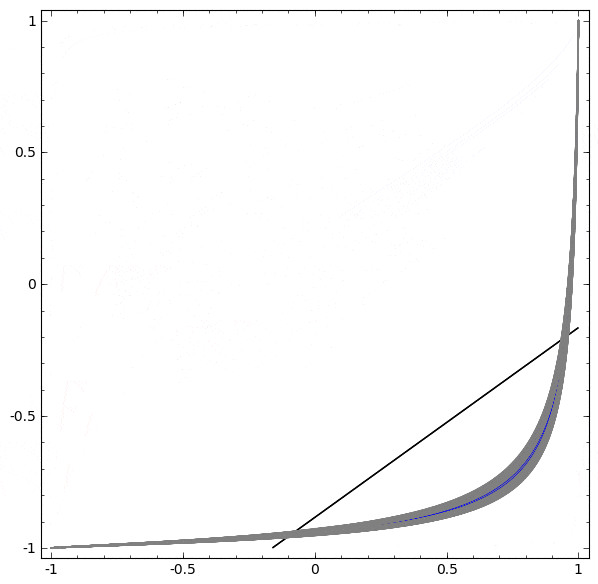
前述したとおり、シグモイド・ユニットやソフトマックス層による分類は、最終的な表現で $A$ と $B$ を分離する超平面（このケースでは直線）を見つけることと同値です。２つの隠れユニットだけでは、ネットワークがこのようにデータを分離することは位相的に不可能であり、このデータセットにおいては失敗する運命です。

以下の可視化では、ネットワークの訓練中の隠れ表現が、分類線とともに見られます。見て取れるように、ネットワークは分類する方法を学習しようと、もがき、仕損ないます。

このネットワークではハードワークは不十分

最終的に、それはむしろ非生産的な極小値に引き込まれます。なお、それは実は約 $\sim 80\%$ の分類精度を達成することができます。

この例では隠れ層を１つしか持っていませんが、隠れ層の数にかかわらず失敗します。

証明：各層は同相写像であるか、行列式0の重み行列を持つ。同相の場合、 $A$ は依然 $B$ に囲まれており、直線でそれらを分離することはできない。しかし、行列式0を持つと仮定すると：データセットはなんらかの軸に潰れる。元のデータセットと同相なものを扱っているため、 $A$ は $B$ に囲まれており、軸に潰れることは、 $A$ と $B$ の点が混ざる点があり、区別できなくなることを意味する。∎

第３の隠れユニットを追加すれば、問題は簡単になります。ニューラルネットワークは以下の表現を学習します：

この表現においては、超平面でデータセットを分離することが可能です。

より深く理解するために、さらに単純なデータセット、１次元のものを考えてみましょう：

A = [-\frac{1}{3}, \frac{1}{3}]
B = [-1, -\frac{2}{3}] \cup [\frac{2}{3}, 1]

２つ以上の隠れユニットの層を使用することなく、このデータセットを分類することはできません。しかし２つのユニットの層を使用すれば、直線でクラスを分離することができる良い曲線として、データを表現することができるようになります：

何が起こっているのでしょうか？１つの隠れユニットは $x > -\frac{1}{2}$ の場合に発火することを学習し、１つは $x > \frac{1}{2}$ の場合に発火することを学習します。１番目が発火し、２番目が発火しなかった場合、 A だと分かります。

##多様体仮説

これは、画像データのような、実世界のデータセットに関連しているでしょうか？本当にまじめに多様体仮説を採用した場合、考察が得られると思います。

多様体仮説とは、自然界のデータがその埋め込み空間の中で、より低次元の多様体を形成する、というものです。これを支持する理論的³ および実験的⁴ 理由があります。これを信じるならば、分類アルゴリズムのタスクは、本質的には、入り組んだ多様体の束を分離することです。

前の例では、１つのクラスが、別のクラスを完全に囲みました。しかし、犬画像の多様体が完全に猫画像の多様体に囲まれているということが、ありそうには思われません。でも、次の節で説明するように、まだ問題を提起することができる、他の、よりもっともらしい位相的状況があります。

##リンクとホモトピー

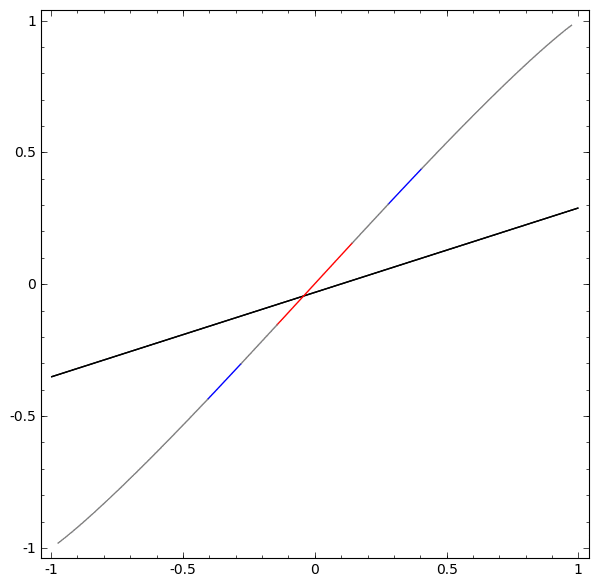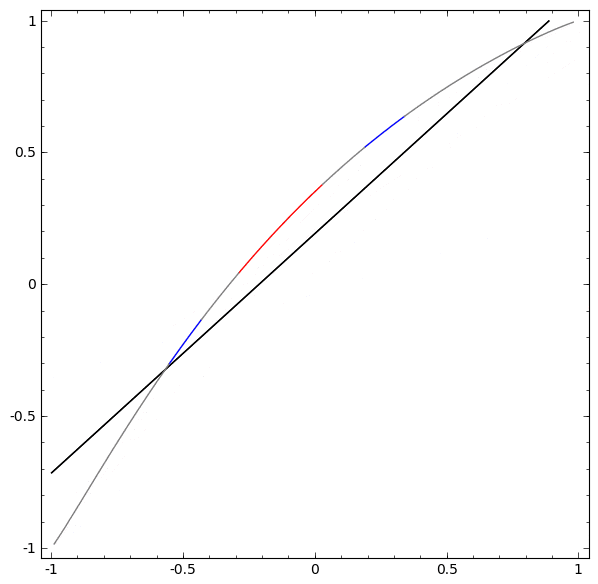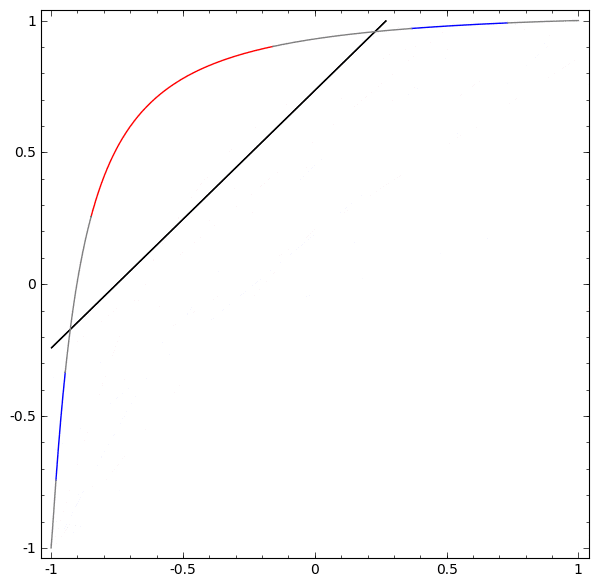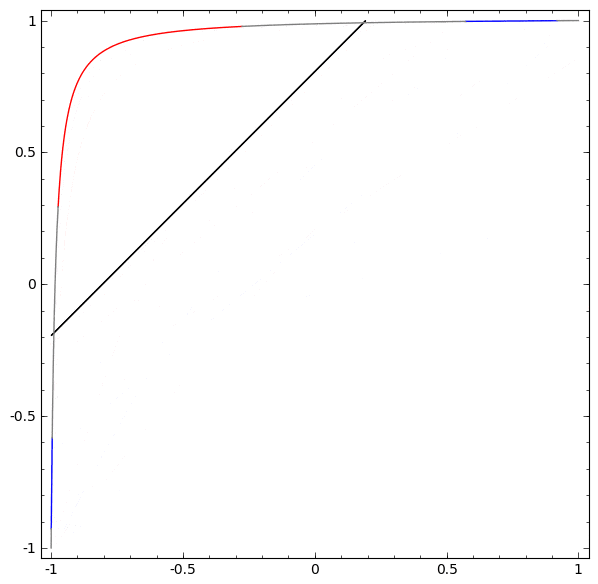
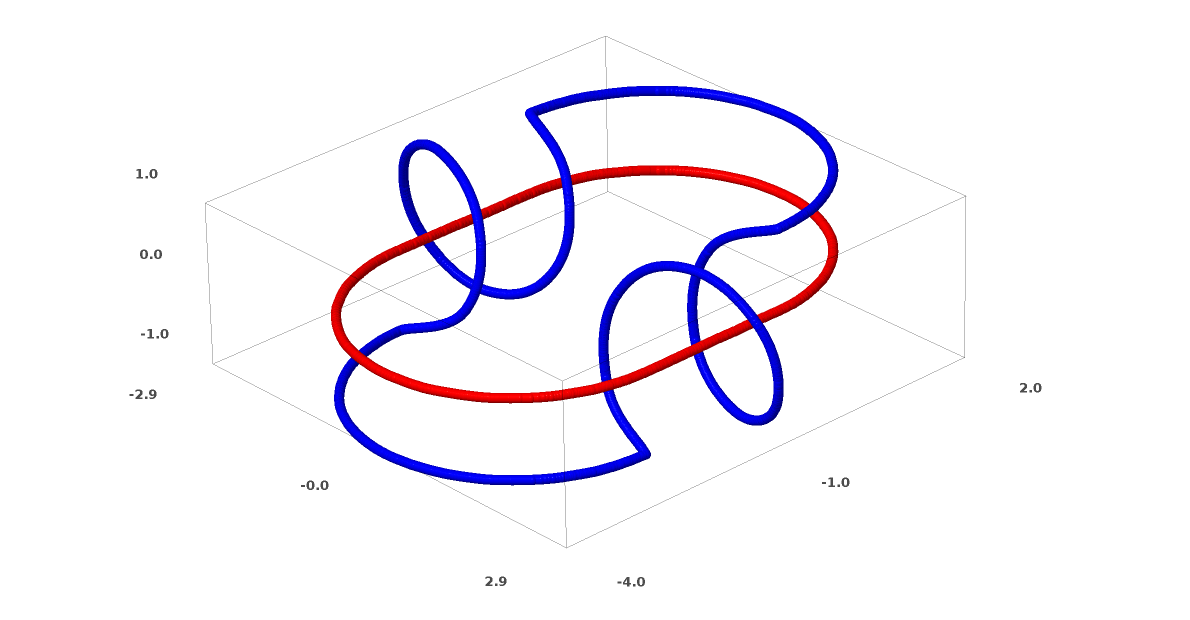
考察することが面白いもう一つのデータセットは、２つの結合されたトーラス、 $A$ と $B$ です。

これまで考えてきたデータセットのように、このデータセットも $n+1$ 次元、すなわち第４次元を使用しなければ分離することはできません。

リンクはトポロジーの１分野、結び目理論で研究されています。リンクを見るとき、時にそれがアンリンク（一緒に絡み合うものの束だが、連続変形により分離可能）であるか否かは明らかではありません。

比較的単純なアンリンク

３ユニットのみの層を用いたニューラルネットワークが分類できる場合、それはアンリンクです。（問題：理論上、すべてのアンリンクは３ユニットのみのネットワークにより分類可能でしょうか？）

この結び目の観点から、ニューラルネットワークによって作られる表現の連続的視覚化は、ただの素敵なアニメーションではなく、リンクをほどく手順です。トポロジーでは、それを、元のリンクと分離されたものの間のアンビエント・アイソトピーと呼びます。

形式的には、多様体 $A$ と $B$ の間のアンビエント・アイソトピーとは、連続関数 $F: [0,1] \times X \to Y$ で、各 $F_t$ が $X$ から値域への同相写像であり、 $F_0$ が恒等写像であり、 $F_1$ が $A$ を $B$ に写すものです。つまり、 $F_t$ は、 $A$ の自分自身への写像から、$A$ から $B$ への写像へ、連続的に遷移します。

定理： a) $W$ が特異ではない、 b) 隠れ層のニューロンを入れ替えて良い、 c) １つ以上の隠れユニットがある、という条件の下で、入力からネットワークの層の表現へのアンビエント・アイソトピーが存在する。

証明：ここでも、ネットワークの各段階を個別に考える：

1. 最も難しい部分は線形変換である。これを可能にするためには、 $W$ が正の行列式を持つ必要がある。前提により行列式は0ではなく、もし負であれば２つの隠れニューロンを入れ替えることにより符号を反転させることができるため、行列式は正として良い。正の行列式を持つ行列の空間はパス連結である。そのため、 $p(0) = Id$ 、 $p(1) = W$ であるような、 $p: [0,1] \to GL_n(\mathbb{R})$⁵ が存在する。各時点 $t$ において $x$ に連続的な遷移行列 $p(t)$ を掛ける関数 $x \to p(t)x$ により、恒等関数から $W$ 変換への連続的な遷移が得られる。
2. 関数 $x \to x + tb$ により、恒等関数から $b$ 並進への連続的な遷移が得られる。
3. 関数 $x \to (1-t)x + tσ(x)$ により、恒等関数から σ の各点適用への連続的な遷移が得られる。∎

このようなアンビエント・アイソトピーを自動的に発見し、リンク同士の同値性や、あるリンクが分離可能かどうかを自動的に証明するプログラムに対する関心が、おそらくあるだろうと、私は想像します。最先端の技術であれば何であれ、ニューラルネットワークで打ち勝つことができるかどうかを知ることは、興味深いことでしょう。

（見たところ、結び目が自明かどうかを決定することはNPです。これはニューラルネットワークにとって良い兆候ではありません。）

ここまで話した種類のリンクは実世界のデータには現れそうにありませんが、より高次元の一般化があります。そのようなものが実世界のデータに存在することは、もっともらしいです。

リンクと結び目は１次元多様体ですが、そのすべてをほどくには４次元が必要です。同様に、 $n$次元多様体の結び目をほどくには、より高い次元の空間が必要です。すべての$n$次元多様体は $2n+2$ 次元でほどくことが可能です。⁶

（私は結び目理論についてあまり知らないため、次元とリンクに関して知られていることについて、より多くを学ぶ必要があります。多様体がn次元空間に埋め込み可能な場合、多様体の次元の代わりにどのような制限があるのでしょうか？）

##簡単な出口

ニューラルネットが行う自然なこと、とても簡単なルートは、単純に多様体を引き離し、絡み合う部分をできるだけ薄く伸ばすことです。しかしこれは真の解法とはほど遠く、相対的に高い分類精度を実現するかもしれませんが魅惑的な局所解でしょう。

それは伸ばそうとしている領域の、とても高い導関数、そして鋭くほとんど不連続な点として、現れるでしょう。それらが起こることが知られています。⁷ 収縮ペナルティ、データポイントにおける層の導関数に対するペナルティは、これに立ち向かう自然な方法です。⁸

トポロジーの問題を解決する観点では、この種の局所最小値はまったく役に立たないため、トポロジーの問題はこれらの課題に立ち向かい探究するための良い動機を提供するかもしれません。

一方、良い分類結果を達成することのみを気にするならば、それは気にならないように思われます。データの多様体の小さなかけらが他の多様体に妨害されているとして、それは問題でしょうか？この問題にかかわらず、任意の良い分類結果が得られるべきであるように思われます。

（私の直観では、このように問題をだまそうとすることは、悪いアイデアです：行き止まりでないと想像することは難しいです。特に、局所最小値が大きな問題である最適化問題において、問題を真に解決することができないアーキテクチャを選択することは悪いパフォーマンスのためのレシピのようです。）

##多様体操作のためのより良い層？

標準的なニューラルネットワークの層、つまり、アフィン変換につづく活性化関数の各点適用によるものを考えれば考えるほど、幻滅を感じます。これらが多様体を操作するために非常に優れているとは想像しがたいです。

おそらく、より歴史的な層の合成に使うことができる、非常に異なる種類の層を持つことは、意味をなすかも知れません？

自然に感じられるのは、多様体をシフトしたい方向のベクトル場を学習することです：

そして、それに基づき空間を変形させます：

固定点（ちょうど、アンカーとして使うために、訓練セットからいくつかの固定点を取ります）におけるベクトル場を学習し、何らかの方法で補間することができます。上のベクトル場の形式は以下のとおりです：

F(x) = \frac{v_0f_0(x) + v_1f_1(x)}{1+f_0(x)+f_1(x)}

ここで、 $v_0$ と $v_1$ はベクトル、 $f_0(x)$ と $f_1(x)$ はn次元ガウシアンです。これは放射基底関数に少しインスパイアされています。

##K近傍層

私はまた、線形分離性がニューラルネットワークの膨大な、そしておそらく無理な、要求であると考え始めました。いくつかの点で、k近傍法（k-NN）を使用することが自然であるように感じます。しかし、k近傍法の成功は分類されるデータの表現に大きく依存するため、k近傍法がうまく機能するより先に良い表現が必要になります。

最初の実験として、私は約$\sim 1\%$のテストエラーを達成したいくつかのMNISTネットワーク（２層畳み込みネット、ドロップアウトなし）を訓練しました。そして最後のソフトマックス層を取り除き、k近傍アルゴリズムを使用しました。一貫して0.1-0.2%のテストエラーの低減を達成できました。

しかし、これはまだ正しいようには感じられません。ネットワークがまだ線形分類をしようとしているにも関わらず、テスト時にk近傍法を使用するため、間違いからわずかに回復できるだけです。

1/距離の重みのため、k近傍法はそれが作用する表現に関して微分可能です。このように、k近傍分類のためにネットワークを直接訓練することが可能です。これは、ソフトマックスの代わりとしてふるまう、「近傍」層の一種と考えることができます。

計算が非常に高価になるため、各ミニバッチのために訓練セット全体にフィードフォワードすることを望みません。私が良いと思うアプローチは、各々に1/(分類対象からの距離)の重みを与えることにより、ミニバッチの各要素をミニバッチの他の要素に基づき分類することです。⁹

悲しいことに、洗練されたアーキテクチャでさえ、単にk近傍法のみを使用した方が5-4%低いテストエラーとなり、シンプルなアーキテクチャではより悪い結果となります。しかし、私はハイパーパラメータの変更にはほとんど力を入れていません。

それでも、ネットワークにするように「求めている」ことが、はるかに合理的に思えるため、私は本当に審美的にこのアプローチが好きです。多様体の超平面による分離可能性とは対照的に、同じ多様体の点が他の多様体の点よりも近いことを求めます。これは、異なるカテゴリーの多様体の間の空間を膨張させ、個々の多様体を収縮させることに一致するはずです。これは単純化のように感じます。

##結論

リンクのような、データの位相的な性質は、ネットワークの深さに関わらず、低次元のネットワークを使用してクラスを線形分離不可能にする場合があります。螺旋のように、技術的には可能でも、とても困難な場合もあります。

ニューラルネットワークを使用してデータを正確に分類するには、幅広い層が必要な場合があります。さらに、従来のニューラルネットワークの層は、多様体の重要な操作を表現するには、あまり良いとは思われません、手動で巧みに重みを設定したとしても、私たちが望む変換をコンパクトに表現することは困難です。機械学習の多様体的観点から動機づけされた新たな層は、有用なサプリメントかもしれません。

（これは、研究開発プロジェクトです。この記事は、オープンな研究を行う中で、実験として掲載しています。これらのアイデアにフィードバックいただければ幸いです：インラインか末尾にコメントできます。タイポ、技術的間違い、追加部分の明確化のため、githubでのプルリクエストを推奨します。）

##謝辞

コメントおよび励ましをくださった、 Yoshua Bengio 、 Michael Nielsen 、 Dario Amodei 、 Eliana Lorch 、 Jacob Steinhardt 、 Tamsyn Waterhouse に感謝します。

---

1. これは、Krizhevsky et al., (2012) から本当に始まったようです。彼らは、優れた結果を達成するために、多くの異なるピースをまとめました。それ以降、多くのエキサイティングな研究があります。 ↩

2. これらの表現は、うまくいけば、データをネットワークで分類する上で「より良く」します。近年、表現を探究する多くの研究がありました。おそらくもっとも魅力的なものは、自然言語処理に関するものです：私たちが単語を理解するということの表現は、単語埋め込みと呼ばれ、面白い性質があります。 Mikolov et al. (2013) 、 Turian et al. (2010) 、 Richard Socherの研究を参照してください。入門として、Turianの論文に関連するとても素晴らしい可視化があります。 ↩

3. 画像に施される多くの自然な変換、例えば、オブジェクトの平行移動やスケーリング、照明の変更などは、連続的に実施した場合、画像空間における連続的な曲線を形成します。 ↩

4. Carlsson et al. は画像の局所的な部分がクラインの壺を形成することを発見しました。 ↩

5. $GL_n(\mathbb{R})$ は実数上の可逆な $n \times n$ 行列の集合で、正式には、位数 $n$ の一般線形群と呼ばれます。 ↩

6. この結果はウィキペディアのサブセクションの Isotopy versions に記載されています。 ↩

7. Szegedy et al. を参照してください、彼らは、データ・サンプルを修正し、最高水準の画像分類ニューラルネットワークがデータを誤って分類する原因となるわずかな変更を見つけることに成功しました。 ↩

8. 収縮ペナルティは収縮オートエンコーダで導入されました。 Rifai et al. (2011) を参照してください。 ↩

9. Theanoで実装することがより実践的であったため、私はこれよりわずかにエレガントではないが、大雑把にいえば同等なアルゴリズムを使用しました：２つの異なるバッチを同時にフィードフォワードし、お互いに基づいてそれらを分類します。 ↩