標準正規分布のロジスティック近似
平均0,分散1の正規分布を標準正規分布という。
この標準正規分布の累積分布関数を$Φ$とすれば、$Φ$は以下のように求められる。
\begin{align}
Φ(y)=\int_{-∞}^{y} \frac{1}{\sqrt{2\pi}}\exp \left( -\frac{x^2}{2} \right) dx
\end{align}
しかし正規分布の累積分布関数は解析的に求められないので、そのままでは逆関数法による乱数の生成などには都合が悪い。そこで近似の出番となる。
$F(y)$を次のようなロジスティック分布の累積分布関数とする。
\begin{align}
F(y)=\frac{1}{1+exp(-0.07056y^3-1.5976y)}
\end{align}
この$F(y)$が上述の$Φ(y)$に近似できることを利用して逆関数法による正規乱数,切断正規乱数の生成をしてみよう。
3次方程式と双曲線関数による実数解
本論に入る前に3次方程式の実数解について触れておきたい。
$p,q$を実数とした上で以下の3次方程式とその判別式について考えよう。
\begin{align}
y^{3}+py=q ・・・(1)
\end{align}
判別式を$D$とすれば、3次方程式(1)の判別式は式(2)となる。
\begin{align}
D=-(4p^{3}+27q^{2}) ・・・(2)
\end{align}
特に$D<0$の場合について。この場合は実数解が1個しかない。
※$p>0$ならば$D<0$となる
そこで、$p>0$の場合の実数解を求めよう。
まず、$h=\sqrt{\frac{4p}{3}}$とした上で、$y=hz$を式(1)に代入する。
\begin{align}
h^{3}z^{3}+hpz=q ・・・(3)
\end{align}
さらに式(3)の両辺について$\frac{3}{hp}$をかけて式整理をすることにより式(4)が得られる。
\begin{align}
4z^{3}+3z=\frac{3q}{2p}\sqrt{\frac{3}{p}} ・・・(4)
\end{align}
ここで双曲線関数の性質を利用する。
双曲線関数とは三角関数と似た性質を持つ以下のような関数だ。
\begin{align}
\sinhθ=\frac{exp(θ)-exp(-θ)}{2}\\
\coshθ=\frac{exp(θ)+exp(-θ)}{2}
\end{align}
「三角関数と似た性質」と書いた通り、これらの関数には倍角公式や逆関数がある。
まず倍角公式について。
\begin{align}
\sinh3θ=4sinh^{3}θ+3sinhθ\\
\cosh3θ=4cosh^{3}θ-3coshθ
\end{align}
$sinhθ,coshθ$の逆関数をそれぞれ$sinh^{-1}θ,cosh^{-1}θ$としよう。
\begin{align}
\sinh^{-1}θ=log(θ+\sqrt{θ^{2}+1})\\
\cosh^{-1}θ=log(θ±\sqrt{θ^{2}-1})
\end{align}
となる。さて式(4)と$sinh3θ$について比較してみよう。
\begin{align}
4z^{3}+3z=\frac{3q}{2p}\sqrt{\frac{3}{p}}\\
4sinh^{3}θ+3sinhθ=sinh3θ
\end{align}
$z=sinhθ,sinh3θ=\frac{3q}{2p}\sqrt{\frac{3}{p}}$に着目すれば
\begin{align}
θ=\frac{1}{3}sinh^{-1}(\frac{3q}{2p}\sqrt{\frac{3}{p}})\\
z=sinh(\frac{1}{3}sinh^{-1}(\frac{3q}{2p}\sqrt{\frac{3}{p}}))
\end{align}
が得られる。$y=\sqrt{\frac{4p}{3}}z$であることから、
\begin{align}
y=\sqrt{\frac{4p}{3}}sinh(\frac{1}{3}sinh^{-1}(\frac{3q}{2p}\sqrt{\frac{3}{p}}))
\end{align}
が得られる。
これが$p>0$の場合の双曲線関数による3次方程式の実数解となる。
逆関数法による乱数生成
$U$を0~1の間の値をとる一様乱数とする。
\begin{align}
U~uniform(0,1)
\end{align}
確率分布の累積分布関数をこの一様乱数で置き換え、逆変換させて乱数を生成する方法のことを逆関数法という。
冒頭のロジスティック近似について思い出してほしい。
\begin{align}
F(y)=\frac{1}{1+exp(-0.07056y^{3}-1.59756y)}
\end{align}
この$F(y)$を一様乱数Uで置き換え、逆変換してみよう。すると、
\begin{align}
y^{3}+\frac{1.59756}{0.07056}y=\frac{-1}{0.07056}log(\frac{1-U}{U})
\end{align}
が得られる。
あとはこの3次方程式を先述の双曲線関数による実数解として求めて、得られた値を乱数として返せばよい。
実際にやってみよう。
以下はRによるコードである。
# ロジスティック近似を利用した逆関数法による正規乱数の生成#
imp_norm<-function(u,s){
U=runif(1,0,1)
p=1.59756/0.07056
q=-1/0.07056*log((1-U)/U)
y=sqrt(4*p/3)*sinh( 1/3*asinh( 3*q/(2*p)*sqrt(3/p) ) )
x=u+s*y
}
N=1000000
x=numeric(N)
X=numeric(N)
for(t in 1:N){
#標準正規乱数#
x[t]=imp_norm(0,1)
#正規乱数;平均4.236,分散2.618#
X[t]=imp_norm(4.236,2.618)
}
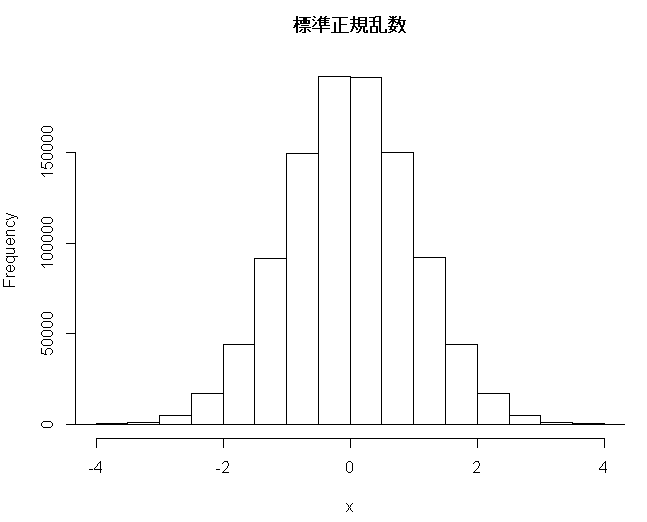
hist(x,xlim=c(-4,4),main="標準正規乱数")
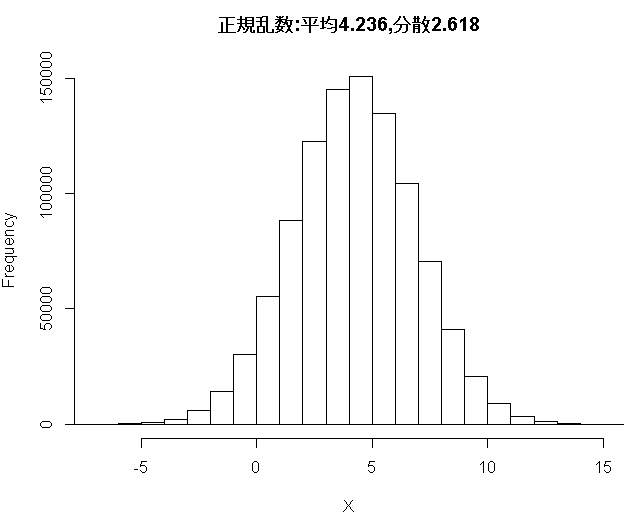
hist(X,xlim=c(-7,15),main="正規乱数:平均4.236,分散2.618")
切断正規乱数の生成
$A≦x≦B$という有限の区間で定義される確率分布を切断分布という。
逆関数法による乱数生成ができるのであれば切断分布の乱数生成も容易にできる。
\begin{align}
F_{A}=\frac{1}{1+exp(-0.07056A^{3}-1.5976A)}\\
F_{B}=\frac{1}{1+exp(-0.07056B^{3}-1.5976B)}\\
F(y)=\frac{1}{1+exp(-0.07056y^3-1.5976y)}
\end{align}
としたとき、切断正規分布の累積分布関数$\hat{F(y)}$は次式となる。
\begin{align}
\hat{F(y)}=\frac{F(y)-F_{A}}{F_{B}-F_{A}}
\end{align}
逆関数法と同様に$\hat{F(y)}$を一様乱数$U$で置き換えて逆変換することで
\begin{align}
y^{3}+\frac{1.59756}{0.07056}y=\frac{-1}{0.07056}log(\frac{1-F_{A}-U(F_{B}-F_{A})}{F_{A}+U(F_{B}-F_{A})})
\end{align}
が得られる。
これも逆関数法と同様に実数解を求めて、得られた値を返せば切断正規分布の乱数となる。
以下Rコード
# 切断正規乱数の生成#
imp_t_norm<-function(u,s,A,B){
U=runif(1,0,1)
p=1.59756/0.07056
FA=1/( 1+exp(-0.07056*((A-u)/s)^3-1.59756*((A-u)/s) ) )
FB=1/( 1+exp(-0.07056*((B-u)/s)^3-1.59756*((B-u)/s) ) )
q=-1/0.07056*log(( 1-FA-U*(FB-FA) )/( FA+U*(FB-FA) ))
y=sqrt(4*p/3)*sinh( 1/3*asinh( 3*q/(2*p)*sqrt(3/p) ) )
x=u+s*y
}
N=1000000
x=numeric(N)
X=numeric(N)
for(t in 1:N){
x[t]=imp_t_norm(0,1,-1.618,2.618)
X[t]=imp_t_norm(4.236,2.618,0,13)
}
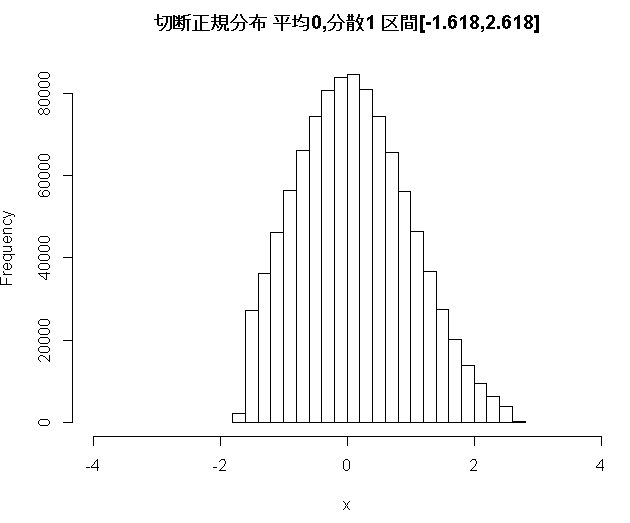
hist(x,xlim=c(-4,4),main="切断正規分布 平均0,分散1 区間[-1.618,2.618]")
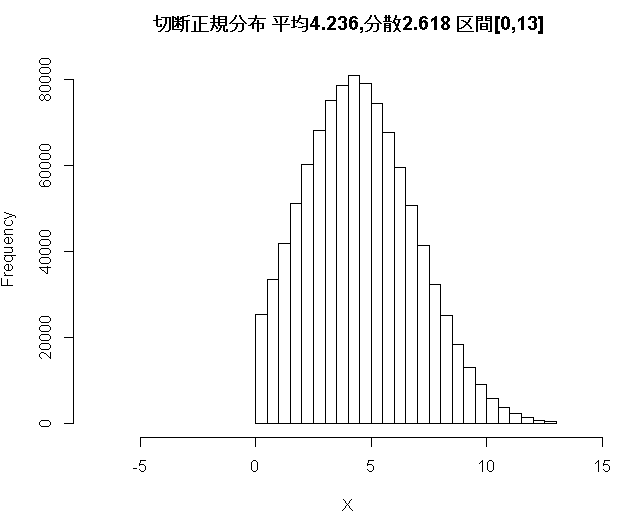
hist(X,xlim=c(-7,15),main="切断正規分布 平均4.236,分散2.618 区間[0,13]")
参考文献
[1]A logistic approximation to the cumulative normal distribution
[Shannon R. Bowling , Mohammad T. Khasawneh , Sittichai Kaewkuekool , Byung Rae Cho (2009) Journal of Industrial Engineering and Management]
[2]Stan Language Reference Manual 2.19
[3]統計分布ハンドブック 増補版[蓑谷千凰彦/朝倉書店]
[4]計算機シミュレーションのための確率分布乱数生成法[四辻哲章/プレアデス出版]
[5]A Survey of Modern Algebra -4th Edition- [Garrett Birkhoff,Saunders MacLane/Akp Classics]