Advent Calendarも残り1週間を切りました.
さてと,私が書く最後の記事になります.今回は,航空宇宙工学の軌道力学が理学物理と異なる点を少しだけ紹介しようと思います.
導入:万有引力の法則
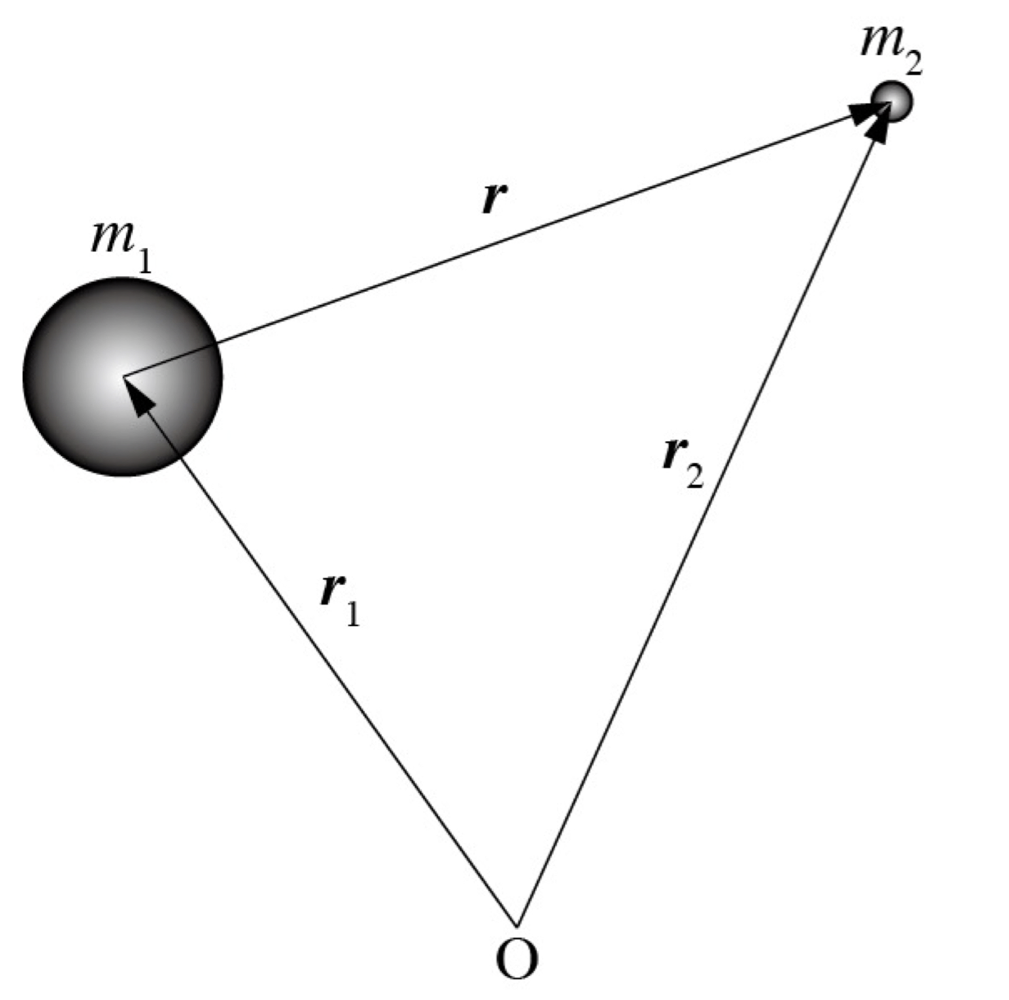
下図に示す物体1・物体2について,万有引力の法則を用いて運動方程式を立ててみます.
\begin{align}
\text{物体1:}\ &m_1 \frac{d^2 \mathbf{r}_1}{dt^2} = \frac{Gm_1 m_2}{|\mathbf{r}_2 -\mathbf{r}_1|^3} (\mathbf{r}_2 -\mathbf{r}_1)
&\cdots \ \text{①}\\
\text{物体2:}\ &m_2 \frac{d^2 \mathbf{r}_2}{dt^2} = \frac{Gm_1 m_2}{|\mathbf{r}_1 -\mathbf{r}_2|^3} (\mathbf{r}_1 -\mathbf{r}_2)
&\cdots \ \text{②}
\end{align}
ここで,②から①を引くことで,物体2の物体1に対する相対的な運動方程式を求めることが出来ます.
\begin{align}
&\frac{d^2 \mathbf{r}}{dt^2} = -\frac{G(m_1 +m_2)}{r^3} \mathbf{r}
&\left( \because \left\{ \text{②}/m_2 \right\} \ - \ \left\{ \text{①}/m_1 \right\} \right)
\end{align}
人工衛星工学の世界では
ここで,物体1が地球や太陽といった質量の大きい自然天体,物体2を人工衛星や探査機といった質量の小さい人工天体とします.このとき,
m_1 \gg m_2
となります.よって,
m_1 + m_2 \fallingdotseq m_1 = m_E
と近似することが出来ます.よって,前節で求めた物体2の物体1に対する相対的な運動方程式を書き直すと,
\begin{align}
&\frac{d^2 \mathbf{r}}{dt^2} = -Gm_E \frac{\mathbf{r}}{r^3} = -\mu \frac{\mathbf{r}}{r^3}
&\cdots \ \text{③}
\end{align}
となります.ここで,
\mu \mathrm{:}重力定数
となります.
航空宇宙工学における軌道力学では,以上の近似を用いることができる場合がほとんどです.従って,質量要素を考慮することは殆どありません.よって,例えば軌道力学における角運動量は,質量をかけずに,
\mathbf{h} = \mathbf{r} \times \mathbf{v}
と表現します.
さいごに
今回は,航空宇宙工学の軌道力学が理学物理と異なる点を少しだけ紹介しました.今まで3回,航空宇宙工学についてのテーマで記事を書いてきましたが,如何だったでしょうか?この機会に,航空宇宙工学に興味を持って頂けたら嬉しいです!
(注)記事の内容は私個人の見解であり,所属する学科組織またはサークルを代表するものではありません.
(注)記事の内容を無断転載・複製する行為は禁じます.