この記事は?
桁 DP って実装のとき頭がこんがらがりませんか?私はこんがらがります。この記事では、桁 DP の実装をなるべく定型化して、実装の際にスムーズに書くことを目的としています。
桁 DP とは
10 進法などで、桁ごとに見て DP テーブルを更新する方法です。大雑把には「$N$ 以下の正整数のうち○○を満たすものについて、△△の和を求めてください。」という形式の問題のうち、○○または△△に、(整数そのものではなく) $10$ 進法などで表したときの各桁(位)の数字によって決まる要素が含まれる問題で使えます。
「各桁(位)の数字によって決まる」というのを、本記事では 桁依存 の要素と呼びます 1 。以下、変数 $N$ はこの意味(調べる対象の上限)で使います。
桁 DP が使える問題:
- $N$ 以下の正整数のうち○○を満たすものについて、△△の和を求めてください
という形式の問題のうち、○○または△△に桁依存の要素を含むもの
なお複数変数の問題も考えられますが、本記事では未対応です。今後元気があれば追記するかもしれません。
例えば、下記のような例が考えられます。
-
カウントタイプ
問題例:「$N$ 以下の正整数のうち、各位の数字 2の和が $K$ の倍数になるものの 個数 を求めよ。」 -
合計タイプ
問題例:「$N$ 以下の正整数のうち、各位の数字 2の和が $K$ の倍数になるものの 合計 を求めよ。」
整数そのものの合計ではなく、なんらかの寄与の合計を求める場合もあります。 -
Leading Zero 考慮タイプ
問題例:「正整数 $a$ について、 $f(a)$ をその数の各位の数字の積とします(例えば
$f(235) = 2\times 3\times 5 = 30$ )。 $\displaystyle\sum_{i=1}^{N} f(i)$ を求めよ。」
この場合、 $235$ を $000235$ などとみなして計算するとゼロになってしまうことから、異なる桁数の正整数を扱う際に Leading Zero の処理に注意が必要になります。
なお Leading Zero 考慮が必要なタイプは議論が複雑になるので、最初は無視して読み進めても本記事の理解には問題ありません。
まとめると次のようになります。
調べる対象
| 調べる対象 | 問題文中の書き方(例) |
|---|---|
| すべて | $N$ 以下のすべての正整数 |
| 整数そのものに依存 | $N$ 以下の正整数のうち $K$ の倍数であるもの |
| 桁依存 | - $N$ 以下の正整数のうち、各位の和が $K$ の倍数であるもの |
| 桁依存 Leading Zero 考慮あり |
- $N$ 以下の正整数のうち、各位の積が $K$ の倍数であるもの |
「桁依存」は何進法で表記するかによって変わる性質のもの、整数依存はそれ以外のものという意味で種類分けしていますが、実際に桁 DP を実装するときには大差はありません。
合計するべきもの
| 合計するべきもの | 問題文中の書き方(例) |
|---|---|
| 個数 | ~~の個数を求めよ |
| 桁依存なし (総和など) |
~~の総和を求めよ |
| 桁依存 | ~~について、「各位の和」の総和を求めよ |
| 桁依存 Leading Zero 考慮あり |
~~について、「各位の積」の総和を求めよ |
「個数」は遷移の際の Factor が常に $1$ になります。
「総和」と「桁依存」は実装上は大差ありません。
ただし Leading Zero 考慮必要 は遷移が少し複雑になります。
上の $2$ つの表から、「調べる対象」と「合計するべきもの」を任意に選ぶと問題ができますが、少なくとも片方に桁依存要素を含む場合には桁 DP が有効です。
種類
いくつか派生のパターンがあります。
-
$10$ 進法か $2$ 進法か
$10$ 進法の他に $2$ 進法などで出題されることもあります。本記事では $b$ 進法 3 ($b = 2,10$ など)で考えるものとします。 $b=2$ の場合は、問題文中に明示的に「$2$ 進法で~~」という直接的な文言が入っておらず、 bitwise xor などで定義される場合もあります。この場合も言い換えると上の形になると思います。 -
「$l$ 以上 $r$ 以下の整数」についての合計を求める場合
$N$ 以下の整数に対する結果を $f(N)$ とおくと、求めるものは $f(r)-f(l-1)$ になるので、本質的には変わりません。
保持するべき情報
桁 DP では次の情報を管理する必要があります。
-
$N$ との大小・一致を表すフラグ
通常の DP とは異なる、桁 DP の本質的な部分です。それまでに見た桁の部分について $N$ との大小関係を保持する必要があります。 DP を上の桁から見る場合は「一致している」か「真に小さい」か、下の桁から見る場合は「超えていない」か「超えている」かを持つとうまくいきます。具体的には次の項で説明します。 -
問題の設定に応じて分類される状態の情報
例えば「$N$ 以下の $K$ の倍数について~~~」という問題では、それまでに見た桁の部分について $K$ で割った余りごとに分類して集計する必要があります。
本記事では、前者($N$ との大小・一致の情報)を flg 、後者(問題固有の分類)を state で表します。
桁 DP では、次のふたつの情報を管理する必要がある
- 見ている範囲での $N$ との大小・一致の関係(
flg) - 問題設定で決まる分類による状況(
state)
N との大小・一致のフラグ
DP の方向として、上の桁から見る方法と下の桁から見る方法があります。それぞれの遷移について説明します。基本的にはどちらでも対応できるので、片方だけマスターすれば大丈夫ですが、比較のためどちらも紹介します。
上から DP の場合
DP テーブル
上の桁から順に見て、 $k$ 番目の桁 4 までの状態がぴったり一致しているかどうかで分けて集計します。
DP[k][flg][state] : $k$ 番目の桁までの状態が flg であり、問題固有の分類による状態が state であるもの
ここで、 flg の意味は下記の通りです。
-
flg = 0:上から $k$ 番目の桁までを見たとき、 $N$ とぴったり一致している -
flg = 1:上から $k$ 番目の桁までを見たとき、 $N$ より真に小さい
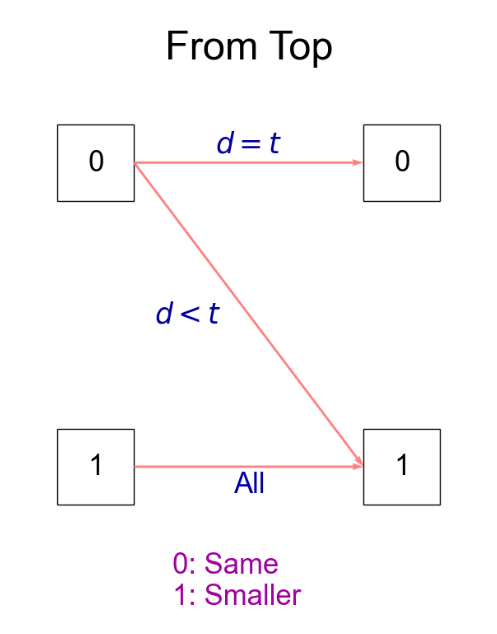
遷移
$N$ の $k$ 桁目の数を $t$ とします。 $k$ 桁目として選ぶ数を $d$ ($d = 0,1,\cdots,b-1$ )とすると、 $k$ 桁目に移る際の遷移は次の図のようになります。一度、真に少ないゾーンに来たらその後はどんな遷移をしても真に少ないゾーン内で動きます。
初期状態と求める状態
- 初期値は
flg = 0 - 求める状態は
flg = 0とflg = 1の合計
下から DP の場合
DP テーブル
下の桁から順に見て、 $k$ 番目の桁 4 までの状態が $N$ の下 $k$ 桁を超えているかどうかで分けて集計します。
DP[k][flg][state] : $k$ 番目の桁までの状態が flg であり、問題固有の分類による状態が state であるもの
ここで、 flg の意味は下記の通りです。
-
flg = 0:$k$ 番目の桁までを見たとき、 $N$ と等しいか小さい -
flg = 1:$k$ 番目の桁までを見たとき、 $N$ より真に大きい
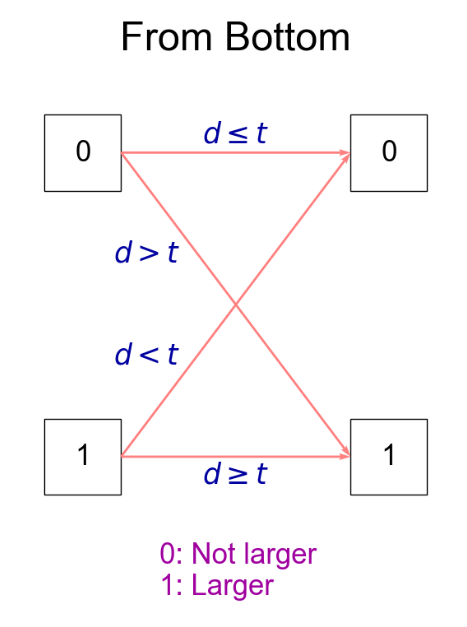
遷移
先ほどと同様、 $N$ の $k$ 桁目の数を $t = t_k$ とします。 $k$ 桁目として選ぶ数を $d$ ($d = 0,1,\cdots,b-1$ )とすると、 $k$ 桁目に移る際の遷移は次の図のようになります。この場合は、先ほどよりも矢印の本数が多くなっています。
初期状態と求める状態
- 初期値は
flg = 0 - 求める状態は
flg = 0
上からと下からの遷移の本数の比較
$b$ 進法で、 $N$ の見るべき桁の数字が $t$ のとき、矢印の本数は下記になります。
- 上から DP の場合は $b+t+1$ 本
- 下から DP の場合は $2b$ 本
$t$ が $0$ 以上 $b-1$ 以下に一様に分布しているとすると、上から DP の場合の期待値は $\displaystyle\frac{3b+1}{2}$ 本となり、下から DP に比べて定数倍($b$ が大きいときで約 $\displaystyle\frac{3}{4}$ 倍)良くなります。
フラグ遷移の数式化
上から・下からいずれの場合でも $\mathrm{flg'}= calc(\mathrm{flg}, d, t)$ が定まります。実装上は、 $t$ を引数として $(\mathrm{flg},\ \mathrm{flg'},\ d)$ の組み合わせを列挙する関数 calc_transition を作っておくときれいに書けます。
for flg, next_flg, digit in calc_transition(target_digit):
# Do something
Leading Zero の考慮が必要な場合
上から DP の場合は、各桁を調べる際に、前の桁からの遷移の他に「新たに桁が発生する」という遷移を加えれば良いです。
下から DP の場合は、各桁を調べ終わった際に、そこで整数が終わったとみなした場合の結果を ans に加えれば良いです。
問題ごとの状態の遷移
問題の設定に合わせて決める状態の遷移については、考えることは通常の DP と同様です。ある状態からの遷移について、遷移先とそこに加える寄与を定める必要があります。寄与は問題によってさまざまな型を取る可能性があり、まとめてひとつの変数で表しても良いのですが、中でもその個数(カウント)については重要なので別にして $c$ 5 としておきます。その他の寄与に関する情報は $v$ 6 とします。また、遷移後のものは「 $'$ 」を付けて表します
まとめると変数は下記です。
- $k$ : 見ている桁の位置を表す。具体的には $b^k$ の位を見ているとする
- $d$ : 見ている桁に適用する数字
- $t$ : 見ている桁に対応する $N$ の数字
- $s$ : 遷移前の state
- $s'$ : 遷移後の state
- $c$ : 遷移前のカウント
- $c'$ : 遷移後のカウント(通常は $c=c'$)
- $v$ : 遷移前の寄与
- $v'$ : 遷移後の寄与
決めるべきこと
次のふたつを決めれば桁 DP の遷移が決まります。
-
状態の遷移先
$s' = f(s, d, k)$ -
個数の計算
遷移前後で個数は変わらないので、count[next_flg][next_state] += count[flg][state]のような更新をすれば良いです。 -
寄与の計算
求めるものが「個数」の場合はこれは不要です。求めるものがなんらかの桁ごとの寄与の合計になっている場合は、桁からの寄与を $g(s, d, k)$ で表すと、 $v' = v + g(s, d, k) \cdot c$ となります。例えば、条件を満たす整数の総和を求める問題では $g(s, d, k)=d \cdot b^{k}$ とすれば良いです 7 。
これらが決まれば DP の遷移が確定します。模式的には下記のようなコードで実行できます。ここで calc_transition は「フラグ遷移の数式化」で定義した遷移を列挙する関数、 f と g は上の 1. と 2. で定義したものです。
for k in range(length_of_N)[::-1]:
target_digit = get_digit(N, k)
for flg, next_flg, digit in calc_transition(target_digit):
next_state = f(state, digit, k)
count[next_flg][next_state] += count[flg][state]
value[next_flg][next_state] += value[flg][state] + count[flg][state] * g(state, digit, k)
計算量
上の実装の場合、遷移部分の計算量は $O(b \log N)$ です。初期化も合わせた全体の計算量は $L$ を state の種類数として $O(b \log N + L)$ です。
実装方法
細かく解説しません 8 。問題例に AC コードのリンクを貼っているので参考にしてください。リンク先の実装では、①遷移・②寄与・③初期状態・④最終状態の条件、の $4$ つを与えるようにしています。個数を数える問題では、寄与の設定は None としています。
問題例と解法(ネタバレ注意)
下記を設定すれば自動的に問題が解けるので、各問題ではこれらの設定方法の例を示します。
- 状態($s$)の定義
- 遷移
$f(s,d,k)$ の形で定義します - 寄与
$g(s,d,k)$ の形で定義します - 初期状態
- 最終状態の条件
分類された状態のうち、これを満たすものの個数(または寄与の合計)が答えになります。
なおこれらのうち 1. は人間が考えるために必要なもので、実際にプログラムで設定する必要があるのは 2.~5. のみです。
問題例 1
問題概要
$N$ 以下の正整数のうち、各桁の数の和が $D$ の倍数であるものの個数を求めよ。
解法
それまでに見た桁の数字の合計を $D$ で割った余りを状態とします。
遷移は $s' = (s + d) \bmod M$ として個数を答えれば良いです。具体的には、次のように設定すれば良いです。
| 決めるべきこと | 定義 |
|---|---|
| 状態($s$)の定義 | これまでに使った桁の数字の合計を $D$ で割った余り |
| 遷移 | $f(s,d,k) = (s+d) \bmod D$ |
| 寄与 | n/a (個数のみ) |
| 初期状態 | $s=0$ |
| 最終状態の条件 | $s=0$ |
問題例 2
ABC154-E Almost Everywhere Zero
AC Code
問題概要
$N$ 以下の正整数のち、$10$ 進法で表したときに $0$ でない数字をちょうど $K$ 個含むものの個数を求めよ。
解法
それまでに見た桁の数字の中で nonzero のものの個数を状態とします。
与えるべき遷移は、 $d=0$ のとき $s' = s$ 、そうでなければ $s'=s+1$ です。
| 決めるべきこと | 定義 |
|---|---|
| 状態($s$)の定義 | 使った数字の中でゼロでないものの個数 |
| 遷移 | $f(s,d,k) = \left\{\begin{array}{ll}s & (d = 0)\\s+1 & (Otherwise)\end{array}\right.$ |
| 寄与 | n/a (個数のみ) |
| 初期状態 | $s=0$ |
| 最終状態の条件 | $s=K$ |
問題例 3
問題概要
整数 $x$ を $10$ 進表記した時に先頭に並ぶ $1$ の個数を $f(x)$ とするとき、$\sum_{i=1}^{N} f(i)$ を求めよ。
解法
| 決めるべきこと | 定義 |
|---|---|
| 状態($s$)の定義 | (上の桁から見て)まだ $1$ しか出ていないとき $0$、そうでないとき $1$ |
| 遷移 | $f(s,d,k) = \left\{\begin{array}{ll}0 & (s=0 \land d = 1)\\1 & (Otherwise)\end{array}\right.$ |
| 寄与 | $g(s,d,k) = \left\{\begin{array}{ll}1 & (s=0 \land d = 1)\\0 & (Otherwise)\end{array}\right.$ |
| 初期状態 | $s=0$ |
| 最終状態の条件 | $s=0$ |
問題例 4
ABC235-F Variety of Digits
TLE Code
$10$ 進法
Leading Zero考慮あり
問題概要
$1$ 以上 $9$ 以下の整数からなる集合 $C$ が与えられる。 $N$ 以下の正整数のうち、 $10$ 進法で表したときに $C$ のすべての要素を含むものの総和を求めよ。
解法
| 決めるべきこと | 定義 |
|---|---|
| 状態($s$)の定義 | $C$ のうちこれまでに見た桁で使ったもの |
| 遷移 | $f(s,d,k) = \left\{\begin{array}{ll}s \cup \{d\} & (d \in C)\\s & (Otherwise)\end{array}\right.$ |
| 寄与 | $g(s,d,k) = d\times 10^{k}$ |
| 初期状態 | $s=\phi$ |
| 最終状態の条件 | $s=C$ |
問題例 5
JOI 2012 Qual-F ジグザグ数
AC Code
問題概要
$A$ 以上 $B$ 以下の整数のうち、 $10$ 進法で表したときに桁の数字がジグザグになっているもの(増加・減少が交互に起こるもの)の総和を求めよ。
解法
| 決めるべきこと | 定義 |
|---|---|
| 状態($s$)の定義 | 最後に使った数字(ただし、初期状態および条件を満たさなくなったものは特殊状態としてそれぞれ $-2$、$-1$ とする) |
| 遷移 | $f(s,d,k) = \left\{\begin{array}{ll}d & (ジグザグ条件を満たすとき)\\-1 & (Otherwise)\end{array}\right.$ |
| 寄与 | $g(s,d,k) = d\times 10^{k}$ |
| 初期状態 | $s=-2$ |
| 最終状態の条件 | $s\geq 0$ |
実装の際の注意・工夫
- ジグザグの種類(偶数桁目で増えるか奇数桁目で増えるか)の $2$ 種類を別々に足す方法もある。その場合は $1$ 桁のものを $2$ 回カウントしてしまうので注意
- 求める対象が $A$ 以上 $B$ 以下なので、 $calc(B) - calc(A-1)$ のようにする。
問題例 6
ABC208-E Digit Products
AC Code
$10$ 進法
Leading Zero考慮あり
| 決めるべきこと | 定義 |
|---|---|
| 状態($s$)の定義 | これまでに使った数字の積 |
| 遷移 | $f(s,d,k) = s\times d$ |
| 寄与 | n/a(個数のみ) |
| 初期状態 | $s=1$ |
| 最終状態の条件 | $s\leq K$ |
- 本問では、状態の種類は大きくないが、 $s$ 自体は大きくなり得るので、辞書などで管理すると良いです。
まとめ
- 「$N$ 以下の正整数のうち○○を満たすものについて、△△の和を求めてください」という形式の問題のうち、○○または△△に桁依存の要素を含む問題では桁 DP が使えることがある
- 桁 DP の問題では、 $N$ との大小・一致を表すフラグと問題固有の分類による状態を管理する必要がある
- 前者の遷移は問題によらず同じ。上の桁から見る方法と下の桁から見る方法があるが、上からの方が遷移が少なく定数倍が良い
- 後者の遷移は問題ごとに異なるので与える必要がある
- ①状態の遷移・②寄与・③初期状態・④最終状態の条件、の $4$ つを設定すれば問題が解ける