この記事でやること
Pythonでトポソを使って全方位DPをするのが目標です。最初にこの記事での実装方針を書いておきます。
実装方法
- トポソを使う
- 抽象化
- 逆元がない場合にも対応
- 左右累積和は配列を1つだけ持つ
- 非再帰
記事としては、2. 抽象化 するための理論面の整備がメインになりそうです。
経緯
前回の記事の最後 に、気が向いたら全方位木 DP も書くと言ったら、早く気が向いてほしいと言われたので気を向けることにしました。
(気が向いてほしいと思っている)
— えびちゃん (@rsk0315_h4x) April 6, 2020
全方位木DPとは
詳細な概念は適当に ググって ください。私は この記事 とかが勉強になりました。
一応イメージを説明すると、各頂点について全方位(親も含むすべての隣接頂点)からの情報に基づいて dp を更新する感じです。具体的には、頂点 $i$ が $k$ 個の隣接頂点 $j_1,\ ...,\ j_k$ を持つときに、 dp[i] が dp[j] たちから計算できるときにこれを使います。ここで ( $i$ が根でないときは) これらの $k$ 個には $i$ の親も含む ことに注意してください。ここが通常の木 DP と異なるところです。
定式化
$(S, f, {\rm unit})$ を可換モノイドとします。すなわち集合 $S$ 上の二項演算 $f: S\times S\rightarrow S$ が
$①\ (単位元)\ \forall a \in S,\ f({\rm unit},\ a) = f(a,\ {\rm unit}) = a$
$②\ (推移律)\ \forall a,\ b,\ c \in S,\ f(f(a,\ b),\ c) = f(a,\ f(b,\ c))$
$③\ (可換律)\ \forall a,\ b \in S,\ f(a,\ b) = f(b,\ a)$
を満たすとします。なおモノイドの演算は「 $\cdot$ 」などの記号で書くことが多いですが、ここでは $f$ を使っています。
ここで複数の $S$ の要素からなる有限集合(空集合でもよい。同じ元を複数もつ場合も別にカウントします。)の、 $f$ による累積 $\tilde f $ を下記で定義します。
$$\tilde f(\{a_1,\ \cdots,\ a_n\})= f( \cdots f(f({\rm unit},\ a_1),\ a_2)\cdots,\ a_n)$$
推移律および可換律より、これは $a_1,\ \cdots,\ a_n$ の順序によらないので、集合 $\{a_1,\ \cdots,\ a_n\}$ について定義されていると見ることができます。
さらに、単項演算 $g: S\rightarrow S$ を考えます。これは次節以降で「調整」と呼びます。
木での定義 1 (根を固定しない場合)
頂点数が $N$ の木を考えます。$i$ の隣接頂点全体の集合を $X[i]$ とします。
まずは 根を固定せず 、一般的に(対称的に?)定義します。
一方向を除く累積
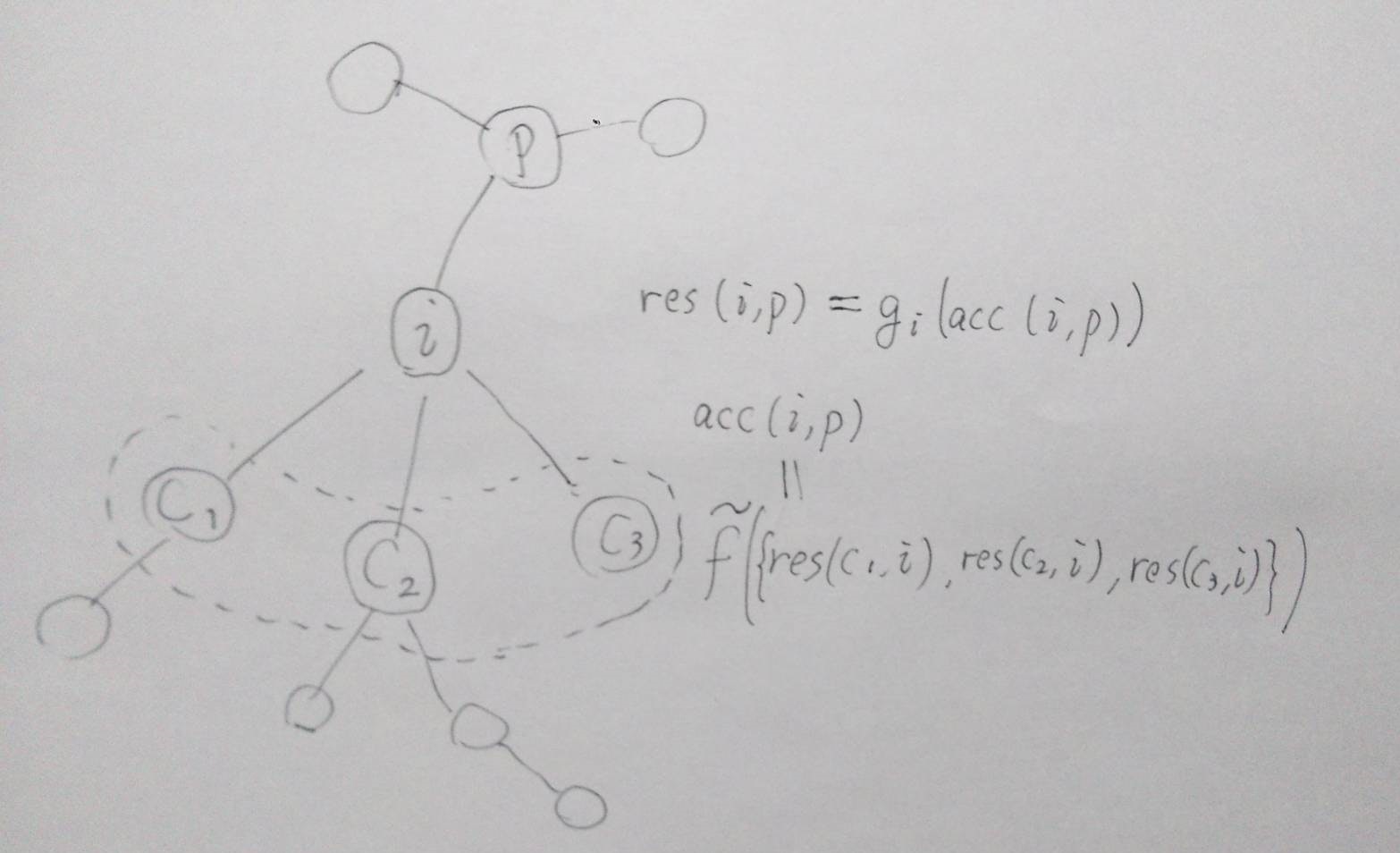
頂点 $i$ とそれに隣接する頂点 $p$ について、 $acc[i][p],\ res[i][p] \in S$ をそれぞれ次のように定義します。
\displaystyle
\begin{align}
acc[i][p] &= \tilde f\Big(\big\{res[c][i]\ \Big|\ c \in X[i] - \{p\}\big\}\Big) & (1) \\
res[i][p] &= g_i(acc[i][p]) & (2)
\end{align}
なお acc 、 res はそれぞれ accumulate 、 result の接頭辞です。イメージ的には、 $acc[i][p]$ は頂点 $i$ の $p$ 方向以外からの集約(調整前)で、 $res[i][p]$ はそれに調整を入れたものです。調整 $g_i$ は $i$ に依存してもよいです。(より広く言うと $i$ の $p$ 以外側の頂点数(サイズ)みたいなのでも大丈夫です。)
ぱっと見、 $(1)$ と $(2)$ がお互いに循環参照しているようにも見えますが、例えば $i$ が葉(次数が1)のとき $acc[i][p] = \tilde f(\phi) = {\rm unit}$ となり定義できます。葉以外も順にちゃんと定義できます。
引数の $p$ および $c$ はそれぞれ parent および child の頭文字ですが、あくまでここでは根を固定していないので $i$ の隣接頂点のうち1つを $p$ と考えていることに注意してください。
全方向の累積
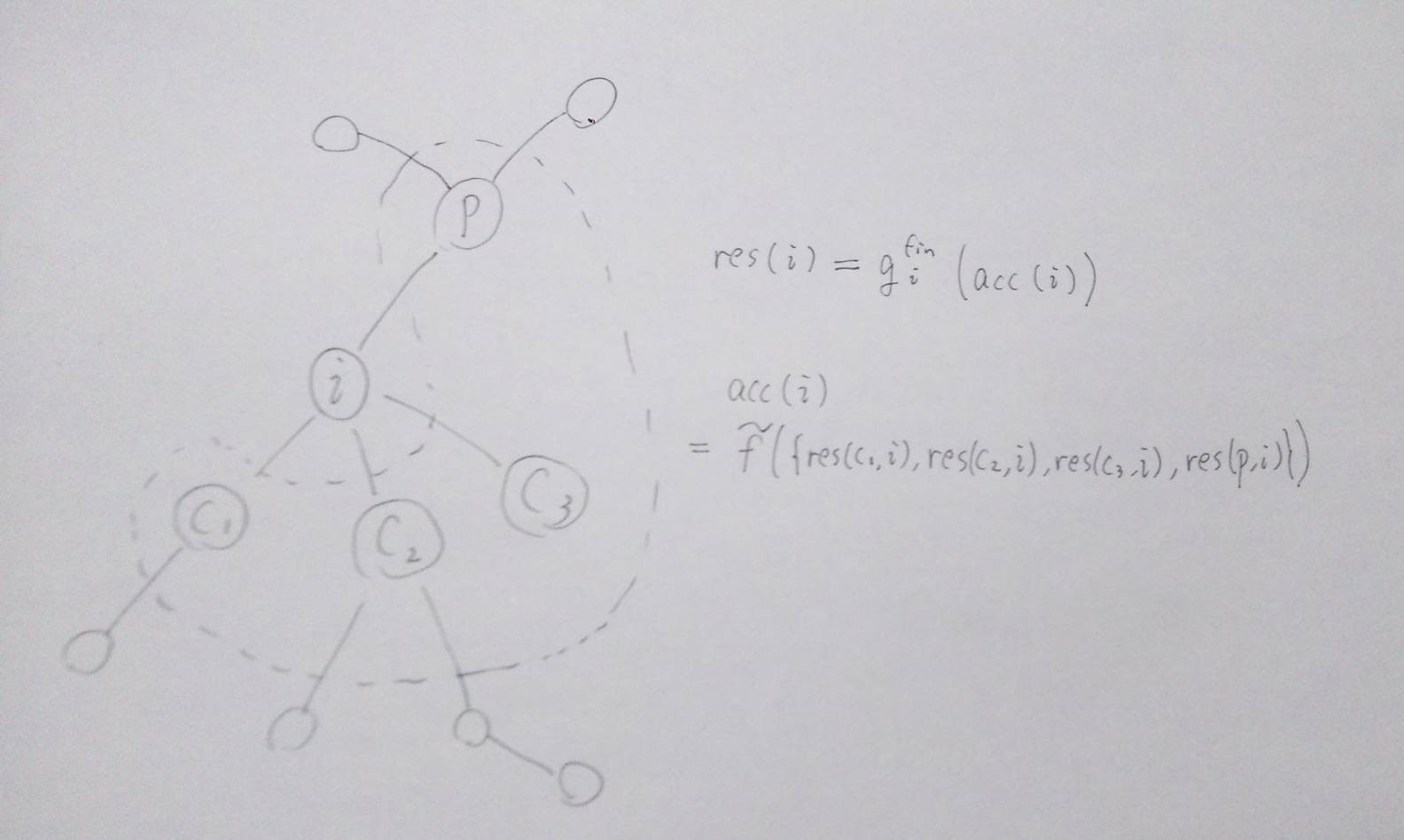
さらに、頂点 $i$ に対して ${acc}[i],\ {res}[i] \in S$ をそれぞれ次のように定義します。
\begin{align}
{acc}[i] &= \tilde f\Big(\big\{res[c][i]\ \Big|\ c \in X[i]\big\}\Big) & (3) \\
{res}[i] &= g^{fin}_i({acc}[i]) & (4)
\end{align}
引数の個数が1つになったこと以外は $(1),\ (2)$ と同じ記号ですが、 ${acc}^{all}$ みたいに書くより分かりやすい気がしたので敢えて同じ記号にしています。イメージは $acc[i]$ は頂点 $i$ の すべての方向からの 集約(調整前)で、 $res[i]$ はそれに調整を入れたものです。最後の調整 $g^{fin}_i$ は $g_i$ と一致すると思っても差し支えないですが、自由度を持たせるため変えています。だんだん 全方位 っぽくなってきましたね。
全方位木 DP の目的は、 各 $i$ について $(4)$ の $res[i]$ を求める ことです。
木での定義 2 (根を固定します)
ここから 根を固定して 考えます。
根でない頂点 $i$ について、 $i$ の親を $p_i$ とします。 $i$ の子全体の集合を $C[i]$ とします。
Bottom-Up DP
上の $(1)$ や $(2)$ の $p$ を $p_i$ で置き換えると次のようになります。
\begin{align}
{acc}^{BU}[i] &:= acc[i][p_i] = \tilde f\Big(\big\{{res}^{BU}[i]\ \Big|\ c \in C[i]\big\}\Big) & (5) \\
{res}^{BU}[i] &:= {res}[i][p_i] = g_i({acc}^{BU}[i]) & (6)
\end{align}
BU は Bottom-Up の頭文字です。
これは 前回 やったみたいに、トポロジカルソートを逆順に見て更新すれば $O(N)$ で計算できますね。
なおここで $acc$ や $res$ は根の取り方によりませんが、 ${acc}^{BU}$ や ${res}^{BU}$ は根の決め方に依存する書き方であることに注意してください。
Top-Down DP
Bottom-Up により、上向きのもの(頂点 $i$ からその親 $p_i$ に向かうもの)の $acc$ と $res$ は計算できました。
$(3)$ および $(4)$ を計算するには下向き(親から来るもの)を求める必要があります。具体的には、
\displaystyle
\begin{align}
{acc}^{TD}[i] &:= acc[p_i][i] = \tilde f\Big(\big\{res[k][p_i]\ \Big|\ k \in X[p_i] - \{i\}\big\}\Big) & (7) \\
{res}^{TD}[i] &:= res[p_i][i] = g_i(acc[p_i][i]) = g_i({acc}^{TD}[i]) & (8)
\end{align}
です。簡単のため $i$ も $p_i$ も根ではないとしておきます。 TD は Top-Down の頭文字です。
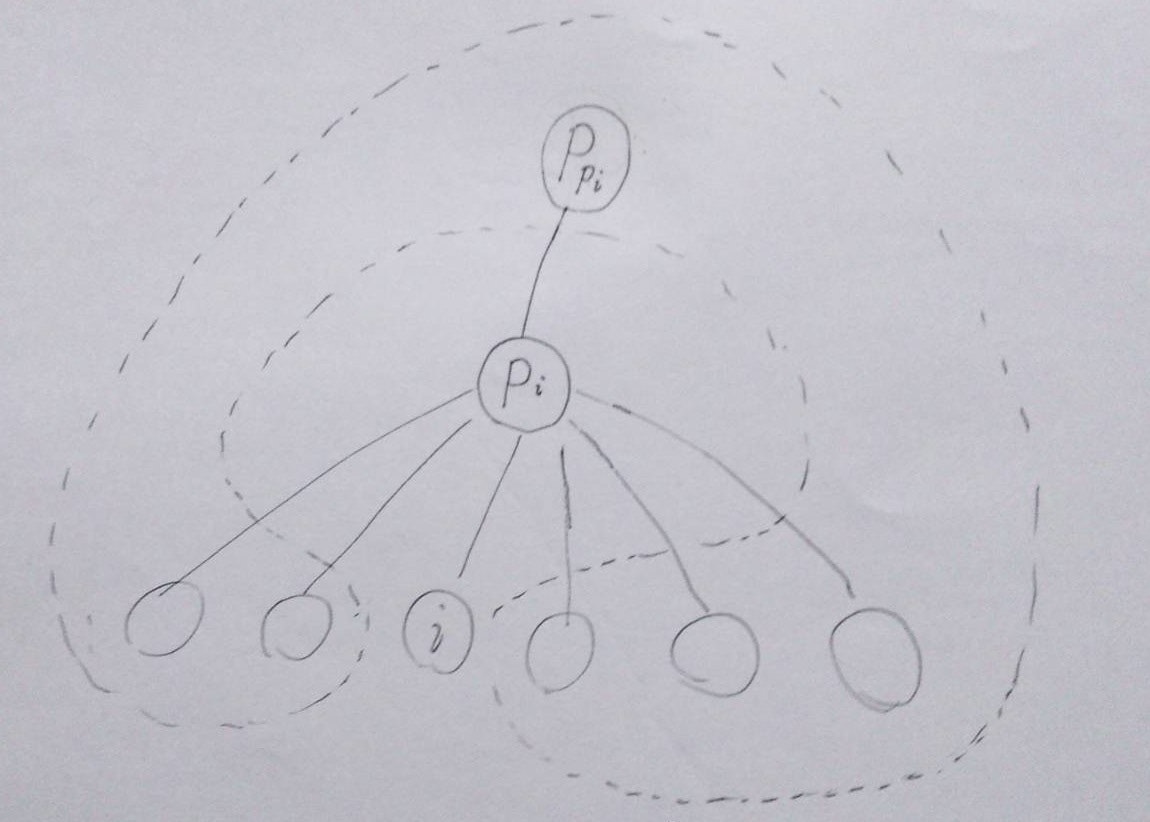
$(7)$ の $\big\{\quad \big\}$ 内を見てみましょう。 $X[p] - {i}$ というのは $p_i$ の隣接頂点のうち $i$ 以外のものなので、 $p_i$ の親 $p_{p_i}$ および $p_i$ の子すべてから $i$ を除いたものすべてからなります。
これを使って $(7)$ を変形するとこんな感じ
\displaystyle
\begin{align}
{acc}^{TD}[i] &= \tilde f\Big(\big\{res[k][p_i]\ \Big|\ k \in C[p_i]\backslash \{i\} \cup \{p_{p_i}\}\big\}\Big) \\
&= f\bigg(\tilde f\Big(\big\{res[k][p_i]\ \Big|\ k \in C[p_i]\backslash \{i\}\big\}\Big),\ res[p_{p_i}][p_i]\bigg) \\
&= f\bigg(\tilde f\Big(\big\{{res}^{BU}[k]\ \Big|\ k \in C[p_i]\backslash \{i\}\big\}\Big),\ {res}^{TD}[i]\bigg) & (9)
\end{align}
この $\tilde f$ の部分をうまく処理しないと、たくさん子がある場合に計算量オーダーが最悪で $O(N^2)$ になってしまいます。ここで 左右累積和 を使うというのが全方位木 DP の定石でしたね。これにより $O(N)$ で計算が可能です。 (なお $f$ や $g$ の逆元を仮定する場合はもっと簡単に書けます。ここではなるべく多くの場面で同じ方法で処理できるように逆元は仮定せず進めることにします。その場合でも多くの場合、計算量オーダーは変わりません。)
Fin
Fin は Final の接頭辞です。 Bottom-Up の結果と Top-Down の結果を統合します。具体的には、 $(3)$ および $(4)$ の定義を思い出して、 BU と TD の結果を使うと
\displaystyle
\begin{align}
{res}[i] &= g^{fin}_i({acc}[i]) \\
&= g^{fin}_i\bigg(\tilde f\Big(\big\{res[c][i]\ \Big|\ c \in X[i]\big\}\Big)\bigg) \\
&= g^{fin}_i\bigg(f({acc}^{BU}[i],\ {acc}^{TD}[i])\bigg)
\end{align}
となり、目標のものが計算できました。
実装
ここから実装(コーディング)します。
EDPC-V を例に説明します。
$acc[i][p]$ を、頂点 $i$ を含む $p$ と逆側の部分木について、「 $p$ を黒で塗った場合に条件を破らない塗り方(*)」の総数とします。具体的には、「 $i$ が黒かつ部分木の黒い頂点は $i$ から黒い頂点のみを通って辿れる」または「部分木のすべての頂点が白」のいずれかです。
本記事の文字で表すと $f(a,\ b) = a\times b$ 、 $g_i(a) = a+1$ とすればよいです ( $g$ は、 $i$ の部分木すべてについての(*)を満たす塗り方の積に、すべて白く塗る場合の1通りを足すので1を足してるんですね。この1を足すのが「調整」です。) 。ただし、最終的な結果はすべて白のものは除く必要があるので、1を足さずに $g^{fin}(a) = g^{fin}_i(a) = a$ (恒等関数)としておきます。
入力部分
前回 の記事と同様です。
N, mod = map(int, input().split())
X = [[] for i in range(N)]
for i in range(N-1):
x, y = map(int, input().split())
X[x-1].append(y-1)
X[y-1].append(x-1)
トポソ部分
前回 の記事と同様です。
P = [-1] * N
Q = deque([0])
R = []
while Q:
i = deque.popleft(Q)
R.append(i)
for a in X[i]:
if a != P[i]:
P[a] = i
X[a].remove(i)
deque.append(Q, a)
設定部分
unit :単位元です。ここでは1です。
merge :本記事の $f$ に相当します。ここでは積を取ります。
adj_bu および adj_td :本記事の $g_i$ に相当します。基本的には同一の式になりますが、 BU と TD で式を分けているのは、「 $i$ の $p$ 以外の方面にある頂点の総数」みたいなのを使う場合があるからです。
adj_fin :最終結果です。本問では、全部白みたいなのが認められないので、最終結果では1を足さないようにしています。
##### Settings
unit = 1
merge = lambda a, b: a * b % mod
adj_bu = lambda a, i: a + 1
adj_td = lambda a, i, p: a + 1
adj_fin = lambda a, i: a
#####
Bottom-Up 部分
ME : merge 関数を使って、本記事の $acc$ を記録します。
XX :メインの DP をする変数です。この Bottom-Up 部分では ${res}^{BU}[i]$ を表しますが、次の Top-Down の部分では最終的に ${res}[i]$ を表します。(なるべく変数を使いまわしてメモリを省略しようとしています。)
ME = [unit] * N
XX = [0] * N
for i in R[1:][::-1]:
XX[i] = adj_bu(ME[i], i)
p = P[i]
ME[p] = merge(ME[p], XX[i])
XX[R[0]] = adj_fin(ME[R[0]], R[0])
# print("ME =", ME) # Merge before adj
# print("XX =", XX) # Bottom-up after adj
Top-Down 部分
全方位木 DP の実装の肝はここです。いろんな実装方法がありますが、本記事では冒頭で書いた通り、「逆元がない場合にも対応」しつつ、「左右累積和は配列を1つだけ持つ」ような実装を紹介したいと思います。
TD :最終的に入るのは本記事の ${res}^{TD}[i]$ に相当します。ただし配列を使いまわしているので、途中では左右累積和の「左から」部分を入れています。 $(9)$ 式の ${res}^{TD}[i]$ も最初からかけています。なお左右累積和は各頂点ごとに $left$ と $right$ の配列を持つ方法もありますが、ここでは全体で大きさ $N$ の配列を1つだけ使っています。
ac :左右累積和を一時的に記録しています。配列として持たず、スカラー変数で所持して順次処理しています。
TD = [unit] * N
for i in R:
# 左からDP(結果はTDに入れている)
ac = TD[i]
for j in X[i]:
TD[j] = ac
ac = merge(ac, XX[j])
# 右からDP(結果はacに入れている)
ac = unit
for j in X[i][::-1]:
TD[j] = adj_td(merge(TD[j], ac), j, i)
ac = merge(ac, XX[j])
XX[j] = adj_fin(merge(ME[j], TD[j]), j)
# print("TD =", TD) # Top-down after adj
# print("XX =", XX) # Final Result
出力部分
adj_fin で最後の調整まで入れておいたので、あとはそのまま出力するだけです。問題によっては、合計を出力する場合などもあるかもしれません。
print(*XX, sep = "\n")
コード全体
ACコード です。
# 全方位木DP
import sys
input = sys.stdin.readline
from collections import deque
N, mod = map(int, input().split())
X = [[] for i in range(N)]
for i in range(N-1):
x, y = map(int, input().split())
X[x-1].append(y-1)
X[y-1].append(x-1)
P = [-1] * N
Q = deque([0])
R = []
while Q:
i = deque.popleft(Q)
R.append(i)
for a in X[i]:
if a != P[i]:
P[a] = i
X[a].remove(i)
deque.append(Q, a)
##### Settings
unit = 1
merge = lambda a, b: a * b % mod
adj_bu = lambda a, i: a + 1
adj_td = lambda a, i, p: a + 1
adj_fin = lambda a, i: a
#####
ME = [unit] * N
XX = [0] * N
TD = [unit] * N
for i in R[1:][::-1]:
XX[i] = adj_bu(ME[i], i)
p = P[i]
ME[p] = merge(ME[p], XX[i])
XX[R[0]] = adj_fin(ME[R[0]], R[0])
# print("ME =", ME) # Merge before adj
# print("XX =", XX) # Bottom-up after adj
for i in R:
ac = TD[i]
for j in X[i]:
TD[j] = ac
ac = merge(ac, XX[j])
ac = unit
for j in X[i][::-1]:
TD[j] = adj_td(merge(TD[j], ac), j, i)
ac = merge(ac, XX[j])
XX[j] = adj_fin(merge(ME[j], TD[j]), j)
# print("TD =", TD) # Top-down after adj
# print("XX =", XX) # Final Result
print(*XX, sep = "\n")
SIZE を使う場合
上でもちらっと書きましたが、 SIZE を使う場合は少し工夫ができます。
具体的には、 adj_bu と adj_tu の式を少し変えれば良いです。大枠は変わらないので、気になる人は ACコード を参考にしてください。下からのときの SIZE は部分木のサイズをそのまま使って、上からのときの SIZE は N-SIZE[i] みたいにすればよいです。
もちろん SIZE 自体もこの全方位 DP で求められるので BU と TD で変えなくても同じ定義でできます。ただ SIZE の TD は BU から簡単に求まるので、下からだけにすると少し高速化できるかもです。
おしまい
完全に自己流なので理論面の説明も実装方法ももっと良い方法があると思います。記事を書く前にいろいろ調べれば良かった。
おしまい