平衡二分木を実装する

回転のいらない平衡二分木を実装したい

Python では組み込み関数に平衡二分木を扱えるものがないので自作する必要があります。よくある平衡二分木では、平衡を保つために「回転」の操作をしないといけないのですが、この処理が実装的にもパフォーマンス的にも結構重いので、なるべく回避する方法を使いたいです。
ここでは、 ピボット値 を設定することで回転のいらない平衡二分木 ¹ を実装する方法を紹介します。 Python のコードも示します。

やりたいこと

• 整数値を取る平衡二分木を作る
• 取りうる整数値 $x$ の範囲を $1\le x< L$ とするとき、構築は $O(1)$ 、挿入・削除・検索は $O(\log L)$ でできる

なお本稿では簡単のため、同じ値を複数個追加することはない（すでに存在する値を追加しようとした場合は何も起きない）としています。
必要な場合、①各整数の個数を管理するための Dict を使う、②IDを末尾に入れて Unique にする、などによって容易に修正できます。問題例2でも扱います。

方針（制約）

通常の二分探索木は、追加の順番によっては片側に伸びてしまって平衡にならないことがあります。平衡を保つためには、ある種の制約を課してやる必要があります。

復習（AVL木、赤黒木）

AVL 木は「どのノードの左右部分木の高さの差も1以下」という制約を課すことで平衡を担保しています。また赤黒木は各ノードに黒または赤の色を対応させて、「赤ノードの子は黒」、「任意の葉から根までにある黒ノードの個数は一定」という制約を課すことで平衡を担保しています。
AVL 木も赤黒木も、制約を満たさなくなると「回転」をすることによって平衡に保つという方法を取っていました。

本稿での制約

扱う整数 $x$ の範囲は $1\le x< L = 2^K$ としておきます。通常の二分探索木の条件に加えて下記を満たすものを「ピボット木（Pivot Tree）」と呼びましょう。

• 各ノードに「ピボット」という値を設定する
• 根のピボット値は $2^{K-1}$
• ピボット値が $p$ （偶数）のノードの左の子のピボット値は $p - {\rm lsb}(p)/2$ 、右の子のピボット値は $p + {\rm lsb}(p)/2$ （＊）
• 各ノードについて、
• 左の子（およびその子孫）の値はピボット値より小さい
• 右の子（およびその子孫）の値はピボット値より大きい

（＊）${\rm lsb}$ は最下位ビットを表します。またピボット値が奇数のノードの子のピボット値は参照されないので何でもいいんですが、ここでは未定義としておきます。参照されないというのは具体例のところを見てもらえると良いと思います。

ピボット木は平衡二分木になります。 より具体的には、高さが $K = \log_2 L$ を超えないことが示せます。

具体例

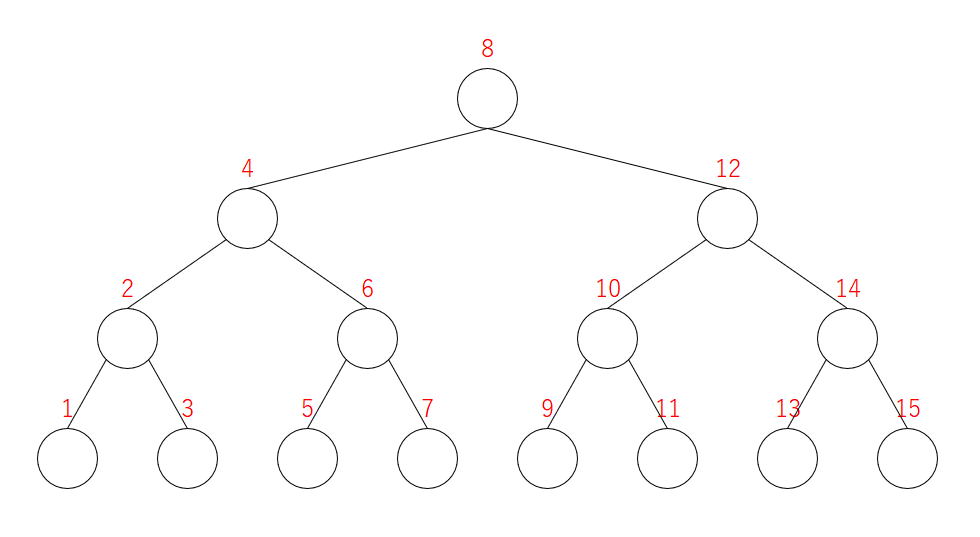
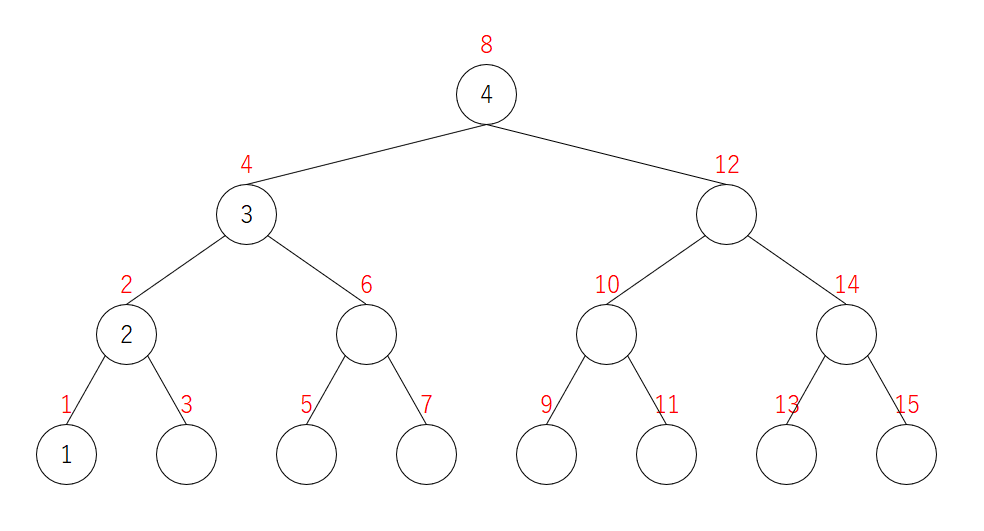
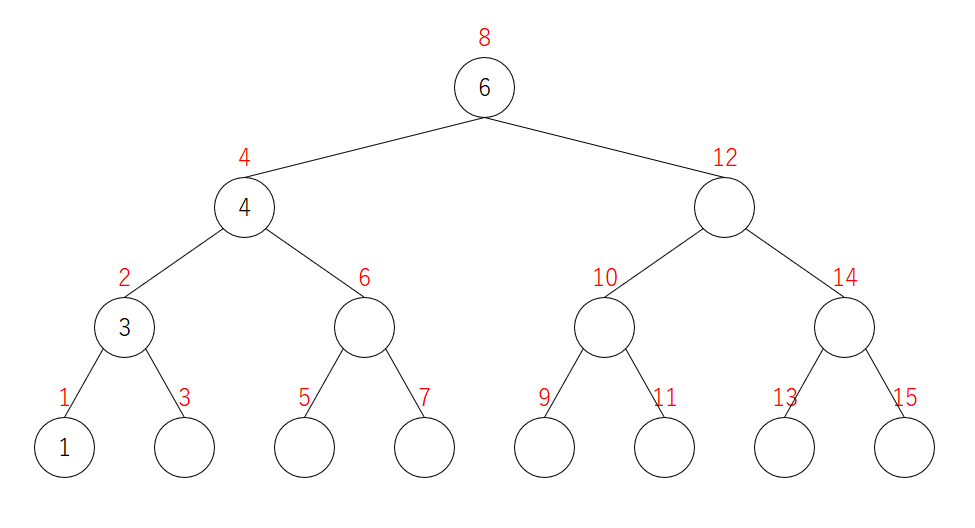
$L = 16,\ K = 4$ としてみましょう。すると、ピボットは次のようになります。

赤字 はピボットを表します。必ずしもその数しか入らない訳ではありません。
ピボットが $a$ である頂点を、単に頂点 $a$ と呼びます。

最初はすべて空欄です。ここから順番に要素を追加していきます。
なお、上の絵ではすべての頂点を最初から描いていますが、実装にあたっては 数が入るところのみノードを追加 すれば良いです。つまり、最初はノードが何もない状態です。

要素の追加

1を追加

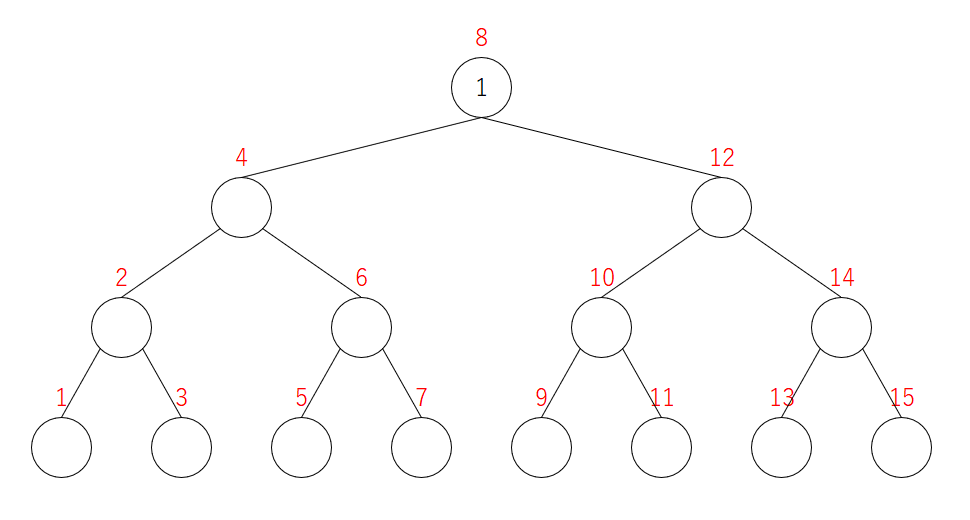
最初は一番上（頂点 $8$ ）に追加します。

2を追加

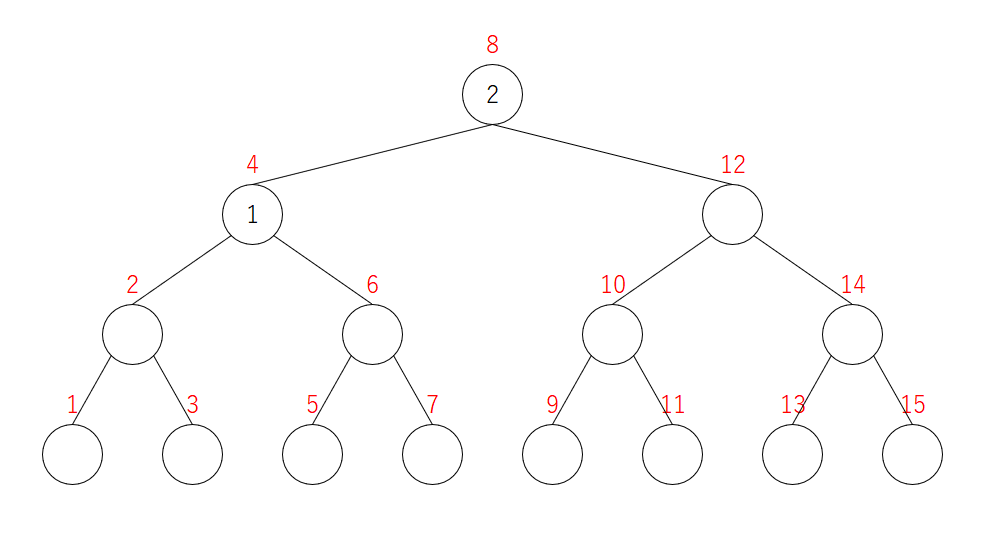
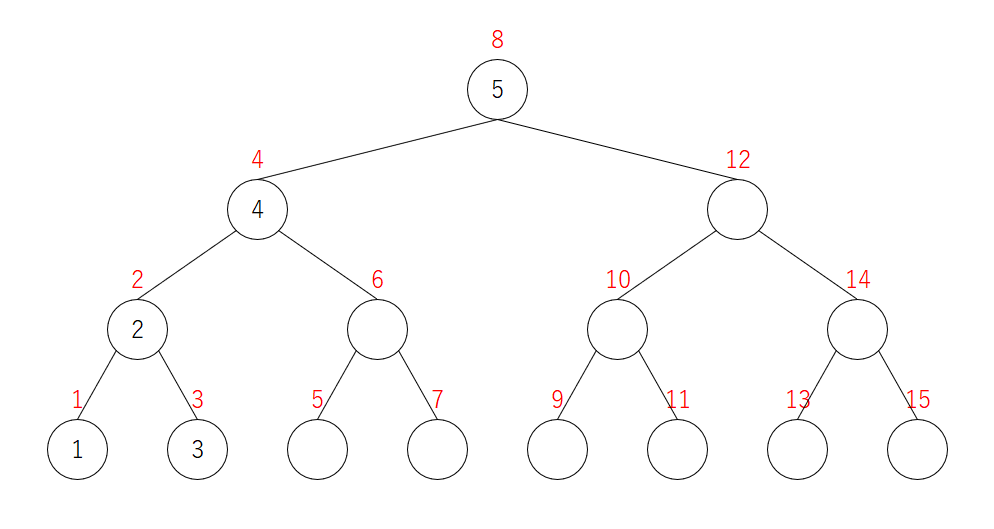
$1$ も $2$ も、頂点 $8$ より右には行けません。ここでは小さい方の $1$ を左の子に移します。

3を追加

左にずれます。

4を追加

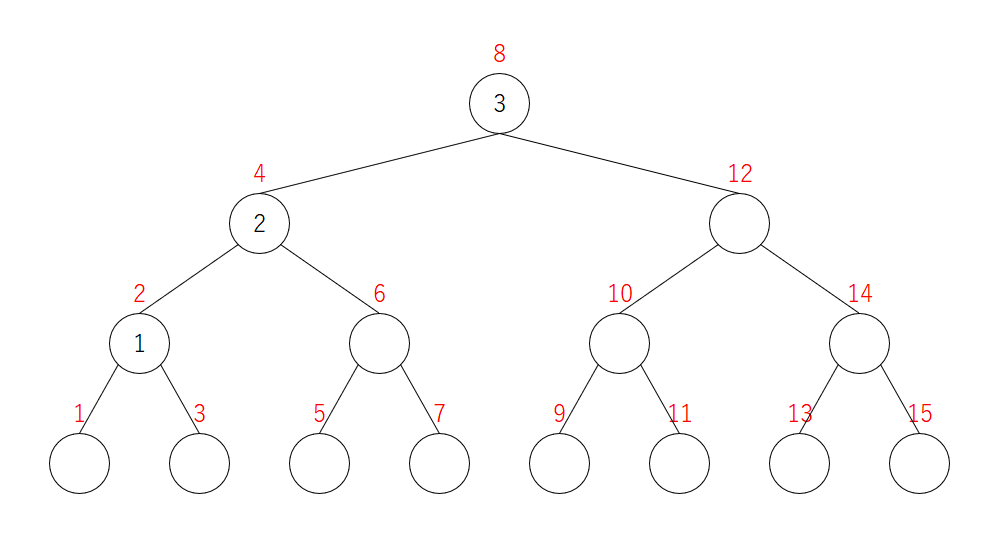
さらに左にずれます。$2$ は、頂点 $2$ に止まります。 $2$ は頂点 $2$ に乗ることはできますが、このどちらの子にも移動できないことに注意してください。
なお $1$ は一番下の段（頂点 $1$ ）に到達しました。ピボット値が奇数の頂点の子のピボットは定義されていませんが、ここにはさらに別の数が降って来ることはないので問題ありません。

5を追加

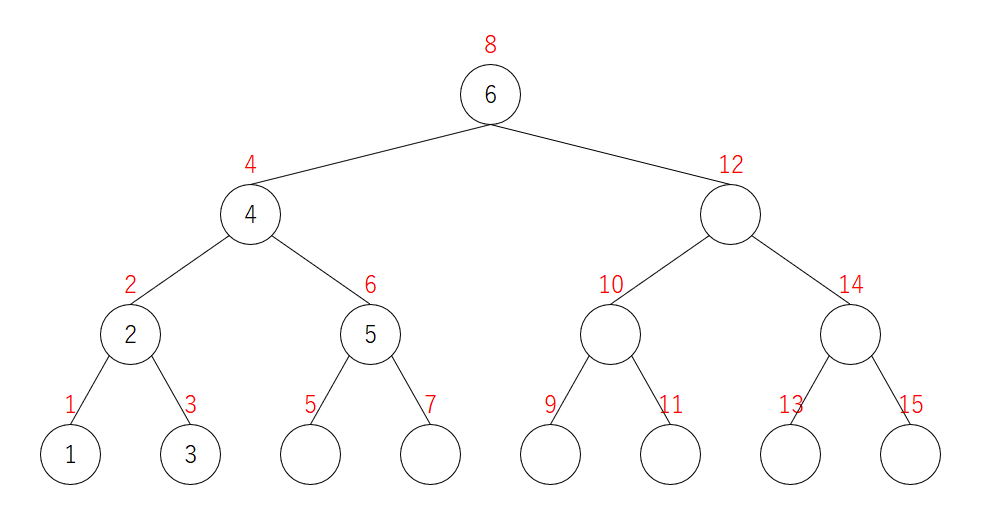
$3$ は頂点 $2$ では右の子に移動します。

6を追加

$5$ は頂点 $4$ では右の子に移動します。
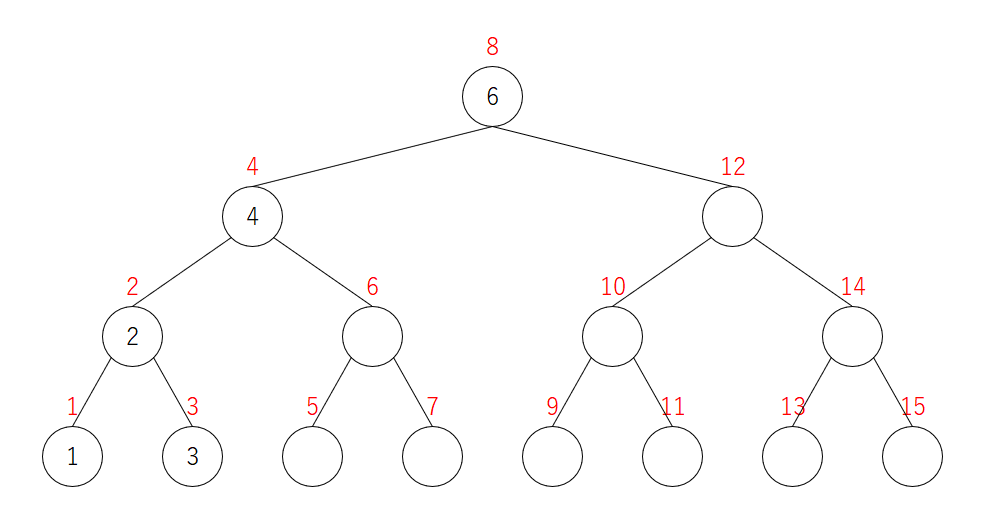
こんな感じで、どんな場合でも $K$ 段目より下に行くことはありません。厳密には、各ノードに入りうる整数の範囲を考えると示せます。

要素の削除

ここから削除です。

5を削除

下に子がなければそのまま削除するだけです。

2を削除

左右に子があれば、（通常の二分探索木の削除と同様に）自分より大きいもののうち最小のものを今いる位置に移動させます。このとき、ピボットの条件が崩れることはありません。
左の子だけある場合は、自分より小さいもののうち最大のものを今いる位置に移動させれば良いです。

要素の検索

ある値以上（以下）の最小（最大）の要素を求めるなどです。これは通常の二分探索木と同様に、根から順に、探したい値がノードの値より小さければ左へ、大きければ右へ行くのを繰り返せば、最悪 $K\ (= \log_2 L)$ ステップでたどり着けます。
全体の中での最小値・最大値も同様に求まります。

問題例

AtCoder の過去問を2つほど紹介します。ネタバレを含みますがご了承ください。

問題例1

CPSCO 2019 1-E （Exclusive Or Queries）

当時 Python / PyPy ではきついと言われてみんなで頑張ってたやつです。

CPSCOのsession1のEをPythonで通そうと頑張ってみたけどダメそうということがわかった(はい)(ごめんなさい)

— てんぷら (@tempura_cpp) May 12, 2019

その後、いろんな人がいろんな方法で通してましたね。 BIT とセグ木という方法もあったと思います。結果的にとても教育的な問題だったと思っています。（ちなみにてんぷらさんもその後通してました。）
私も平衡二分木の整備のきっかけになったので良かったです。

ACコード → ■

取りうる整数の範囲が $10^9$ 程度あるので座圧する手もありますが、本稿の方法だとしなくても大丈夫です。
なおこの問題では、「すでに存在する値を追加しようとした場合」に、その値を削除するようにしています。

問題例2

ABC170-E

$K = 48$ つまり追加されうる整数の種類が　$2^{48} - 1$ の平衡二分木を20万本ほど使っています（構築自体は $O(1)$ でできるので、このようにたくさん持つこともできます）。 $48$ ビットのうち、上位 $30$ ビットはメインの整数（問題文でいう「レート」）を表し、下位 $18$ ビットは幼児の ID を表します（重複があるとめんどくさいので ID をつけて区別しています）。 区別するためだけに $K$ を増やして定数倍がもったいないと思うかもしれませんが、実際には上位 $30$ ビットの時点で要素が区別されるので、ピボット木は $30$ 段程度までしか必要ありません。 → よく考えたら元の整数が全部一致してたりするとだめですね（汗）

ACコード → ■

なおこの問題は検索が最小値（または最大値）のみなので heapq でも実装できるため、平衡二分木はややオーバーキル感もありますが、遅延処理が不要になるため（ライブラリを持っていれば）実装はラクになります。

heapqを用いる方法 → ■

実装

上に書いたとおり内部的には $1\le x < L$ を扱っていますが、実際には $0$ を扱いたいことも多いので、実装では値を $1$ ずらして保持しています。つまり外から見ると $0$ 以上 $L-2\ (=2^K-2)$ 以下の整数を扱えるようにしています。
また、要素が1つもないと場合分けがめんどいので、ダミーの根として ${\rm inf} = L - 1$ （ずらし後）を必ず入れるようにしています。

test.py

class BalancingTree:
    def __init__(self, n):
        self.N = n
        self.root = self.node(1<<n, 1<<n)

    def append(self, v):# v を追加（その時点で v はない前提）
        v += 1
        nd = self.root
        while True:
            if v == nd.value:
                # v がすでに存在する場合に何か処理が必要ならここに書く
                return 0
            else:
                mi, ma = min(v, nd.value), max(v, nd.value)
                if mi < nd.pivot:
                    nd.value = ma
                    if nd.left:
                        nd = nd.left
                        v = mi
                    else:
                        p = nd.pivot
                        nd.left = self.node(mi, p - (p&-p)//2)
                        break
                else:
                    nd.value = mi
                    if nd.right:
                        nd = nd.right
                        v = ma
                    else:
                        p = nd.pivot
                        nd.right = self.node(ma, p + (p&-p)//2)
                        break

    def leftmost(self, nd):
        if nd.left: return self.leftmost(nd.left)
        return nd

    def rightmost(self, nd):
        if nd.right: return self.rightmost(nd.right)
        return nd

    def find_l(self, v): # vより真に小さいやつの中での最大値（なければ-1）
        v += 1
        nd = self.root
        prev = 0
        if nd.value < v: prev = nd.value
        while True:
            if v <= nd.value:
                if nd.left:
                    nd = nd.left
                else:
                    return prev - 1
            else:
                prev = nd.value
                if nd.right:
                    nd = nd.right
                else:
                    return prev - 1

    def find_r(self, v): # vより真に大きいやつの中での最小値（なければRoot）
        v += 1
        nd = self.root
        prev = 0
        if nd.value > v: prev = nd.value
        while True:
            if v < nd.value:
                prev = nd.value
                if nd.left:
                    nd = nd.left
                else:
                    return prev - 1
            else:
                if nd.right:
                    nd = nd.right
                else:
                    return prev - 1

    @property
    def max(self):
        return self.find_l((1<<self.N)-1)

    @property
    def min(self):
        return self.find_r(-1)

    def delete(self, v, nd = None, prev = None): # 値がvのノードがあれば削除（なければ何もしない）
        v += 1
        if not nd: nd = self.root
        if not prev: prev = nd
        while v != nd.value:
            prev = nd
            if v <= nd.value:
                if nd.left:
                    nd = nd.left
                else:
                    #####
                    return
            else:
                if nd.right:
                    nd = nd.right
                else:
                    #####
                    return
        if (not nd.left) and (not nd.right):
            if not prev.left:
                prev.right = None
            elif not prev.right:
                prev.left = None
            else:
                if nd.pivot == prev.left.pivot:
                    prev.left = None
                else:
                    prev.right = None

        elif nd.right:
            # print("type A", v)
            nd.value = self.leftmost(nd.right).value
            self.delete(nd.value - 1, nd.right, nd)    
        else:
            # print("type B", v)
            nd.value = self.rightmost(nd.left).value
            self.delete(nd.value - 1, nd.left, nd)

    def __contains__(self, v: int) -> bool:
        return self.find_r(v - 1) == v

    class node:
        def __init__(self, v, p):
            self.value = v
            self.pivot = p
            self.left = None
            self.right = None

    def debug(self):
        def debug_info(nd_):
            return (nd_.value - 1, nd_.pivot - 1, nd_.left.value - 1 if nd_.left else -1, nd_.right.value - 1 if nd_.right else -1)

        def debug_node(nd):
            re = []
            if nd.left:
                re += debug_node(nd.left)
            if nd.value: re.append(debug_info(nd))
            if nd.right:
                re += debug_node(nd.right)
            return re
        print("Debug - root =", self.root.value - 1, debug_node(self.root)[:50])

    def debug_list(self):
        def debug_node(nd):
            re = []
            if nd.left:
                re += debug_node(nd.left)
            if nd.value: re.append(nd.value - 1)
            if nd.right:
                re += debug_node(nd.right)
            return re
        return debug_node(self.root)[:-1]

BT = BalancingTree(5) # 0 ～ 30 までの要素を入れられるピボット木
BT.append(3)
BT.append(20)
BT.append(5)
BT.append(10)
BT.append(13)
BT.append(8)
BT.debug()
BT.delete(20)
BT.debug()
print(BT.find_l(12)) # 10
print(BT.find_r(5)) # 8
print(BT.min) # 3
print(BT.max) # 13
print(3 in BT) # True
print(4 in BT) # False
BT.debug_list()

# 愚直チェック
from random import randrange
BT = BalancingTree(5) # 0 ～ 30 までの要素を入れられるピボット木
S = set()
for _ in range(1000):
    a = randrange(31)
    if randrange(2) == 0:
        BT.append(a)
        S.add(a)
        
    else:
        BT.delete(a)
        if a in S: S.remove(a)
    if BT.debug_list() != sorted(list(S)):
        print("NG!!")
    # print(BT.debug_list(), sorted(list(S)))
print("END")

その後 solzard さんにいくつか指摘してもらったので修正しました（上のコードにも反映してます）。

find_min(), find_max()は@propertyとして定義することで、bt.find_min() -> bt.minのようにスッキリします。
パフォーマンスに変化はなくお好みですが、def行の上に@propertyと付けるだけなのでオススメです

— solzard (@solzard_) June 15, 2020

さらに chineristAC さんにも指摘もらったので修正しました（反映がめちゃくちゃ遅くなりました）。ランダムチェックも入れてみましたが今度こそちゃんと動いてそうです。

こんにちは
本当に今更？って感じの遅い指摘で申し訳ないのですが、
削除したいノードの左右どちらかがない場合の処理がKiriさんの実装だとピボットの対応がおかしくなってしまいそうです
たとえばL=4として2,1,6,5,10,9,14,13の順に削除して追加しなおすと画像のようになってしまいました pic.twitter.com/cIwoYVNmwd

— chineristAC (@ChineristA) August 16, 2020

値が実数のとき

実数範囲でも同様のピボット木を作ることはできます。ただし、オーバーフローには注意する必要があります。有理数型を使うなどしてオーバーフローの問題は解決されるかもしれませんが、とても近い範囲にたくさんの要素が集中すると、平衡が保たれなくなってしまいます。
上では、ピボットは1段下りるごとにちょうど半分ずつになるように設定しましたが、特定の位置に要素が固まりやすいことが分かっていれば必ずしもそうする必要はありません。具体的には、実数 $x$ の確率分布が与えられると、累積分布関数がぴったり等分される位置に設定すると効率が良いです（でもほとんどの場合は定数倍の差しかないと思います）。

1. この記事では「平衡」は高さが要素数の対数オーダーで抑えられる、ぐらいの意味で使っています。 ↩