この記事の目的

オンライン畳み込み（Relaxed Convolution ¹ または Relaxed Multiplication ² などとも呼ばれるようです）を $O(N(\log N)^2)$ で処理する方法について書きます ³ 。

畳み込みがオンラインとは、 $A$ および $B$ の各項が前から順に与えられたとき、その都度、畳み込み $C=A*B$ の各項を順に返すことを言います ⁴。詳細は後述します。

（復習）畳み込み

まずは通常の（オフラインの）畳み込みの復習をします。
数列 $(c_0,\ c_1,\cdots)$ が $(a_0,\ a_1,\cdots)$ と $(b_0,\ b_1,\cdots)$ の畳み込みであるとは、各 $i$ について

$$
c_i = \displaystyle\sum_{j=0}^{i} a_j \times b_{i-j}
$$

が成立することでした。あるいは、べき級数の言葉では

$A(x) = a_0 + a_1 x + a_2 x^2 + \cdots$
$B(x) = b_0 + b_1 x + b_2 x^2 + \cdots$
$C(x) = c_0 + c_1 x + c_2 x^2 + \cdots$

について、 $C(x)=A(x) \times B(x)$ が成立するとも言えます ⁵ ⁶ 。

$A(x)$ および $B(x)$ の最初の $N$ 項が与えられたとき、 $C(x)$ の最初の $N$ 項を求めることは FFT により $O(N\log N)$ でできます。

オンライン畳み込み

やりたいこと

冒頭で書いた通り、やりたいことは下記です。

$C(x)=A(x) \cdot B(x)$ とします。$q=0,\ 1,\ 2, \cdots,\ N-1$ の順に下記を処理してください。

$a_q$ および $b_q$ が与えられるので $c_q$ を返してください。

$c_i = \sum_{j=0}^{i} a_j \times b_{i-j}$ に従って愚直に計算すると $q$ 番目のクエリの計算量が $\Theta(q)$ 、合計で $\Theta(N^2)$ になってしまうので高速で処理するには工夫が必要です。

工夫

$A$ と $B$ の項をいくつかまとめて畳み込みをすると FFT の恩恵が受けられます。
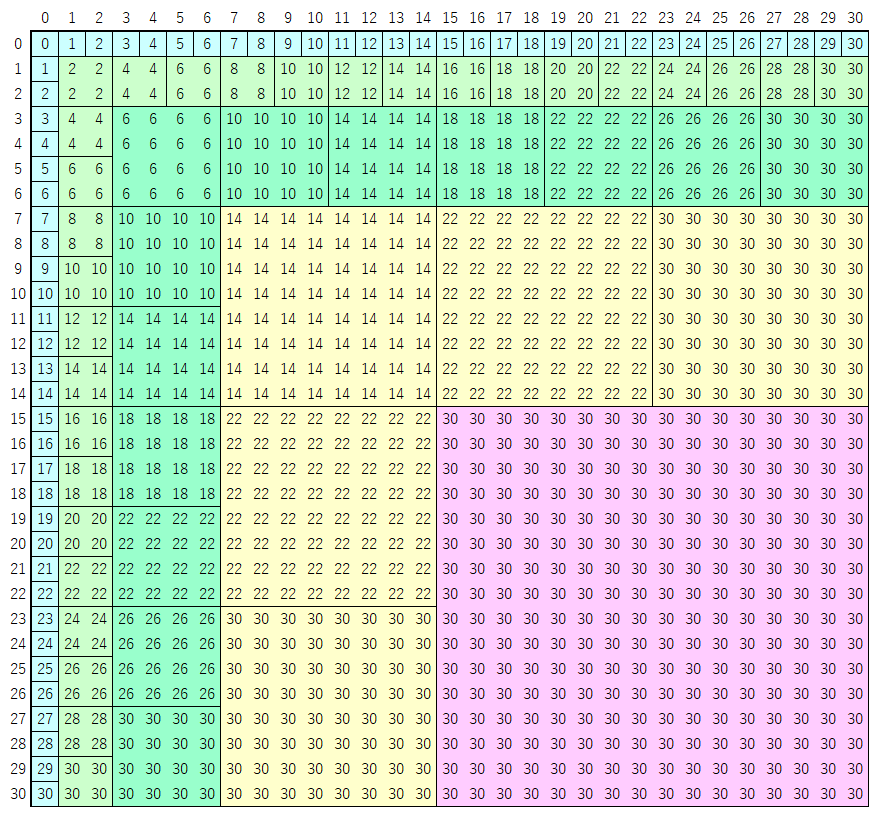
具体的には次の表のようにまとめて計算します ¹ ⁷。表の見方は、上から $i$ 番目、左から $j$ 番目のセルを $q_{i,j}$ とすると、$A(x)$ の $i$ 次の項と $B(x)$ の $j$ 次の項の積を $q_{i,j}$ 番目のクエリの際に計算することを示しています。

次の 2 点が成立することからうまくいくことが分かります。

$q_{i,j} \ge \max(i, j)$ が成立する、すなわち畳み込みをする際には必要な係数の情報が揃っている
$q_{i,j} \le i+j$ が成立する、すなわち各クエリの処理後には必要な計算が終わっている

例えば、表中で $6$ が出てくるのは次の $5$ つの正方形部分です。

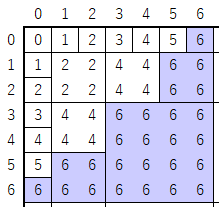
つまり $q=6$ 番目のクエリを処理する際には、

$a_0 \times b_6 x^6$
$(a_1 x+a_2 x^2)\times (b_5 x^5+b_6 x^6)$
$(a_3 x^3 +a_4 x^4 +a_5 x^5+a_6 x^6)\times (b_3x^3+b_4x^4+b_5x^5+b_6x^6)$
$(a_5x^5+a_6x^6)\times (b_1x+b_2x^2)$
$a_6x^6 \times b_0$

に対応する部分の畳み込みをすればよいです。

計算量

簡単のため $N=2^K-1$ とすると、一辺が $2^k$ の正方形は $2^{K-k+1}-1$ 個あるので、 FFT を使うとこの部分は $O(2^K \cdot k) \in O(N\log N)$ で処理できます。全体の計算量は $O(N (\log N)^2)$ です。

実装

各クエリでどの大きさの正方形まで処理するかが分かれば良いです。これは $q+2$ の lsb ⁸ を見ると分かります。ただし $q=2^k-2$ 型のときは最後の大きさの正方形が 1 つだけになり別処理が必要です。

コード

Python によるコードの例を示します。

test.py

P = 998244353
p, g, ig = 998244353, 3, 332748118
W = [pow(g, (p - 1) >> i, p) for i in range(24)]
iW = [pow(ig, (p - 1) >> i, p) for i in range(24)]
 
def convolve(a, b):
    def fft(f):
        for l in range(k, 0, -1):
            d = 1 << l - 1
            U = [1]
            for i in range(d):
                U.append(U[-1] * W[l] % p)
 
            for i in range(1 << k - l):
                for j in range(d):
                    s = i * 2 * d + j
                    t = s + d
                    f[s], f[t] = (f[s] + f[t]) % p, U[j] * (f[s] - f[t]) % p
 
    def ifft(f):
        for l in range(1, k + 1):
            d = 1 << l - 1
            U = [1]
            for i in range(d):
                U.append(U[-1] * iW[l] % p)
 
            for i in range(1 << k - l):
                for j in range(d):
                    s = i * 2 * d + j
                    t = s + d
                    f[s], f[t] = (f[s] + f[t] * U[j]) % p, (f[s] - f[t] * U[j]) % p
 
    n0 = len(a) + len(b) - 1
    if len(a) < 50 or len(b) < 50:
        ret = [0] * n0
        if len(a) > len(b): a, b = b, a
        for i, aa in enumerate(a):
            for j, bb in enumerate(b):
                ret[i+j] = (ret[i+j] + aa * bb) % p
        return ret
    
    k = (n0).bit_length()
    n = 1 << k
    a = a + [0] * (n - len(a))
    b = b + [0] * (n - len(b))
    fft(a), fft(b)
    for i in range(n):
        a[i] = a[i] * b[i] % p
    ifft(a)
    invn = pow(n, p - 2, p)
    for i in range(n0):
        a[i] = a[i] * invn % p
    del a[n0:]
    return a
 
class RelaxedMultiplication():
    # h = f * g
    def __init__(self):
        self.f = []
        self.g = []
        self.h = []
        self.n = 0
    
    def calc(self, l1, r1, l2, r2):
        self.h += [0] * (r1 + r2 - 1 - len(self.h))
        for i, a in enumerate(convolve(self.f[l1:r1], self.g[l2:r2]), l1 + l2):
            self.h[i] = (self.h[i] + a) % p
        
    def append(self, a, b):
        self.f.append(a)
        self.g.append(b)
        self.n += 1
        n = self.n
        m = (n + 1) & -(n + 1)
        s = 0
        if m <= n:
            a = 1
            while a <= m:
                self.calc(n - a, n, s, s + a)
                self.calc(s, s + a, n - a, n)
                s += a
                a <<= 1
        else:
            a = 1
            while a < m >> 1:
                self.calc(n - a, n, s, s + a)
                self.calc(s, s + a, n - a, n)
                s += a
                a <<= 1
            self.calc(n - a, n, s, s + a)
        return self.h[n-1]

Semi-Relaxed

$A(x)$ と $B(x)$ のうち片方は最初から与えられているとき Semi-Relaxed と言ったりするようです ² 。
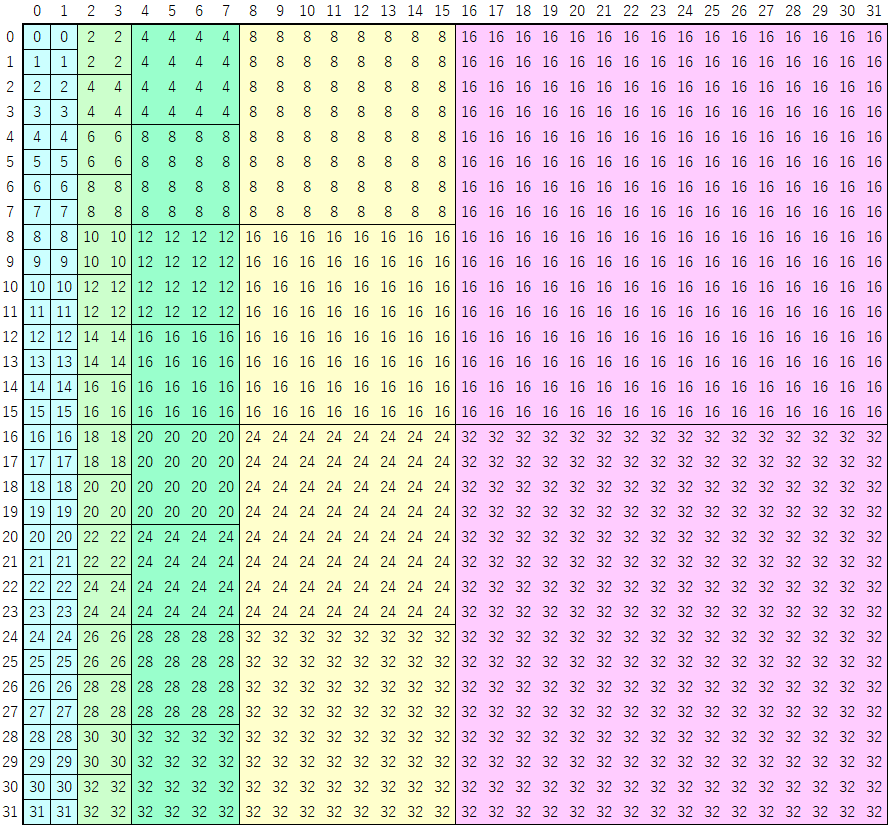
$B$ 側が固定の場合、先ほど出てきた条件のうち「 $q_{i,j} \ge \max(i, j)$ 」が「 $q_{i,j} \ge i$ 」に緩められます。

$q_{i,j} \ge i$ が成立する、すなわち畳み込みをする際には必要な係数の情報が揃っている
$q_{i,j} \le i+j$ が成立する、すなわち各クエリの処理後には必要な計算が終わっている

すると右側方向には「フライング」ができるのでより効率よく計算することができます。例えば下記のようにすると良いです ⁷ 。
オーダーは変わらず $O(N(\log N)^2)$ です。

DFT の結果のメモ化

（2023/1/14 追記）
$A$ と $B$ の畳み込みをする際、 $\mathrm{iDFT}(\mathrm{DFT}(A) \cdot \mathrm{DFT}(B))$ のように計算しますが、上の分割方法では同じ $A$ に対する $\mathrm{DFT}$ を何度も使っていることが分かります。これをメモ化することで定数倍改善ができます。

メモなし (6.1s)

メモあり (4.7s)

Middle Product

（2023/1/14 追記）

$n=2^k$ とします。長さ $n$ の配列と長さ $2n-1$ の配列を畳み込むとき、もし結果のうち真ん中の $n$ 項のみしか使わないのであれば、長さ $n$ の配列ふたつの畳み込みと同じ大きさで計算できます。普通に $2n$ の大きさで DFT・iDFT を行えば（左側の $n-1$ マスと右側の $n-1$ マスは重なるものの）真ん中 $n$ マスは重ならないのでそのまま使える感じです。

これを使うとより効率的に計算できるようです。

My implementation is not such beautiful, and there is no need to "compute the whole rectangle", we could use the "middle product" trick and "compute the triangle", which is enough. https://t.co/bXr5X1E8kQ
— hly1204 (@yeye39618806) January 7, 2023

具体的には、例えばこのように分割します ⁹ ¹⁰ 。

あるいは、小さいところは愚直で行うことにすると、次のように行う方法もあります。図では水色部分（ $2^2$ 未満の範囲）を愚直で行うこととしています。

こちらもオーダーは変わらず $O(N(\log N)^2)$ ですが、主要部の定数倍が良いです。
下記はいずれもメモ化してます。

Normal Product (4.7s)
Middle Product (2.9s)

さらに iFFT するところをまとめてやるワザもあります。

maspy さんに教えてもらった線形性を使うテクやると、赤部分 2 つのの戻し（iFFT）をまとめてできる。主要部分の定数倍が 3/4 pic.twitter.com/3T8f8Rq0L3
— きり (@kiri8128) January 23, 2023

Semi-Relaxed の場合はこんな感じにできます。

オンライン畳み込みを使ったその他の処理

（2023/1/14 追記）

inverse などもオンラインに求めることができます。

[x^i]f, [x^i]g を与えるごとに [x^i](fg) を得る
を利用して、inverse, division, pow, log, exp なども同様のことができるものを用意した。
— maspy (@maspy_stars) November 17, 2022

具体的なアルゴリズムは hotman さんの記事が参考になります。

オンライン畳み込み

この記事の目的

（復習）畳み込み

オンライン畳み込み

やりたいこと

工夫

計算量

実装

コード

Semi-Relaxed

DFT の結果のメモ化

Middle Product

オンライン畳み込みを使ったその他の処理

関連問題