こんにちは。以前の記事で球面上で一様な乱数を生成するための方法を紹介しました。Ray-Taracingにおいて、これでは不十分なことが多いのでHemispherical Importance Sampling Monte Carlo Methodを紹介します。こちらの記事と照らし合わせながら導出します。(https://qiita.com/KionIm/items/08589a22c2daa5490f8b)
目次
[1.Hemispherical Importance Sampling Monte Carlo Method](#1-Hemispherical Importance Sampling Monte Carlo Method)
[2.Cosine-Weighted Hemisphere Sampling](#2-Cosine-Weighted Hemisphere Sampling)
3.おわりに
1. Hemispherical Importance Sampling Monte Carlo Method
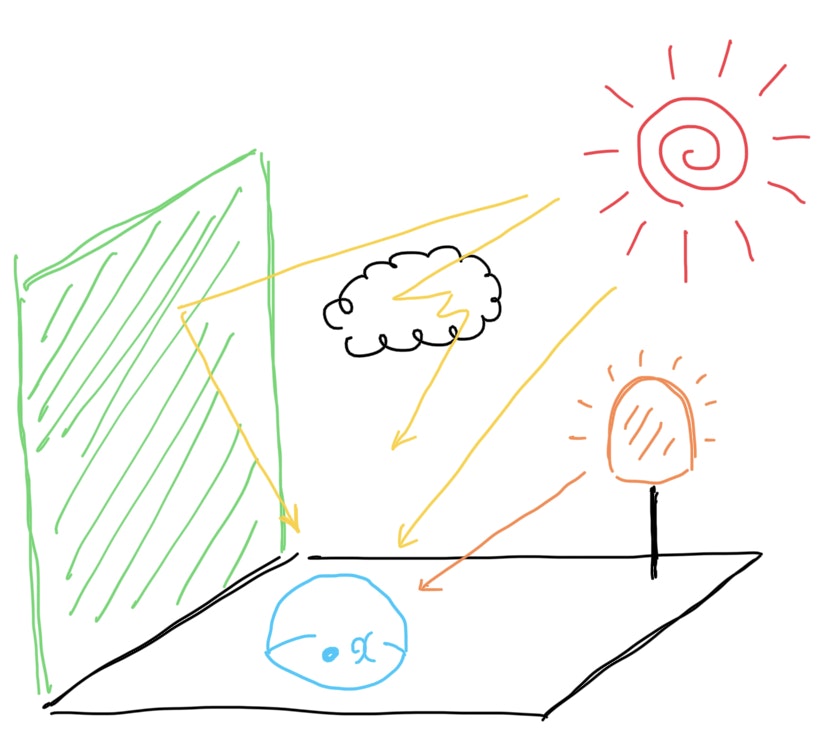
図にあるように、ある点$x$の色はオブジェクトの色と周囲からの光の影響から成る。しかし、青線で描いた半球に入射する光が$x$の色に対して全て等しい重みで寄与していると考えると、水平線付近からの寄与が不自然に大きくなってしまう。そのため、天頂付近からの寄与が大きくなるように新たなMonte Carlo法を考える。これがHemispherical Importance Sampling Monte Carlo Methodである。
2. Cosine-Weighted Hemisphere Sampling
半球面上で一様に生成された乱数が全て等しい重みを持っているとは$p(\omega) = 1/2\pi$であるということだ。同じように、天頂に近いほど重みを大きくするには$~p(\omega) \propto \cos \theta $ のような分布の確率密度を与えればよい。
\begin{align}
\int_{\mathcal{H}_2} p(\omega) d\omega
&= \int^{2\pi}_0 \int^{\frac{\pi}{2}}_0 c~\cos\theta \sin\theta d\theta d\phi \\
&= 2\pi c\int^{\frac{\pi}{2}}_0 \cos\theta \sin\theta d\theta \\
&= \pi c = 1
\end{align}
このことと、参考先の(3)を用いると、
c = \frac{1}{\pi}~,~~~p(\omega)=\frac{1}{\pi}\cos \theta~,~~~p(\theta,\phi) = \frac{1}{\pi} \cos \theta \sin\theta
となる。次は、確率密度関数を変数ごとに分離します。
p(\theta) = \int^{2\pi}_0 p(\theta, \phi) d\phi = \int^{2\pi}_0 \frac{1}{\pi} \cos\theta \sin \theta d\phi = 2\sin \theta \cos \theta
p(\phi) = p(\phi|\theta) = \frac{p(\theta,\phi)}{p(\theta)} = \frac{1}{2\pi}
次は、累積密度関数を計算する手順となるが、経度方向は一様乱数分布なので緯度方向$~p(\theta)~$のみを考える。
P(\theta) = \int^{\theta}_0 p(\theta') d\theta' = \sin^2 \theta
$u = P(\theta)$とすると、
u = \sin^2 \theta~,~~v = \frac{\phi}{2\pi}
一様乱数(0,1)に従う($u,v$)を与えることで、確率密度に従った($\theta,\phi$)が生成される。ここで生成される($\theta,\phi$)は天頂付近にサンプルが集中しており、以下のようにMonte-Carlo法を計算することで、球面上で一様なサンプルを取得するよりも少ないサンプル数で現実に近い結果(irradiance)が得られる。
\left< F^N\right> = \frac{1}{N} \sum^{N-1}_{i=0} \frac{f(\theta,\phi)}{p(\omega)}
3. おわりに
今回は理論のみの紹介だが、今後は実装についても紹介していきたい。