カイ二乗分布と適合度検定

はじめに

下記について解説し、例題を用いてPythonで実装する。
・カイ二乗分布
・適合度検定

カイ二乗分布について

確率変数 $Z_{1}$, $Z_{2}$,..,$Z_{n}$が互いに独立で、標準正規分布に従うとき
次の式から導かれる統計量$χ^2$ が従う確率分布のこと（確率密度関数は割愛します）

$χ^2 = Z_{1}^2 + Z_{2}^2 + Z_3^2 $+ .. + $Z_{k}^2$ (自由度k)

適合度の検定

理論上の確率分布(度数に関する分布)に対して、標本から求めた度数(観測度数)が適合しているかを検定すること。
例えば、理論上の確率分布がばらつきに偏りのないもの(一様分布)だった場合、観測度数も偏りがないはずであるということ。
観測度数が確率分布に適合している仮説の下で、近似的に下記が成立することを元に検定を行う。

$\sum_{i=1}^k(x_{i} - np_{i})^2 / np_{i} $　～$χ^2$ (自由度k-1)

※ x:観測度数、np:期待度数

例）
1～5の数字が書かれたくじを20回選んでもらった。特定の数字が多く出ているか検定せよ。

import pandas as pd

# 標本のdf
df = pd.DataFrame(
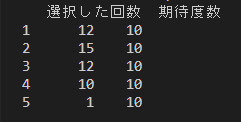
    {"選択した回数(観測度数)": [12, 15, 12, 10, 1], "期待度数": [10, 10, 10, 10, 10]},
    index=[1, 2, 3, 4, 5]
)
print(df)

出力結果

検定統計量$χ^2$を計算する。

result = 0
for row1, row2 in zip(df["選択した回数(観測度数)"], df["期待度数"]):
    result += (row1 - row2)**2 / row2
print(result)

>>> 11.399999999999999

自由度4のカイ二乗分布の5%水準の統計量は、9.49。
したがって、5%水準で有意差あり。
理論上の確率分布に従っているという仮定に無理があったと言える。
※今回の場合の理論上の確率分布は、1～5がすべて確率$\frac{1}{10}$ という一様分布のこと。