はじめに
去年の7月にRを使った事後分布のMCMCによるサンプリング①というタイトルでメトロポリスヘイスティングによるサンプリングを実行し、そのコードを投稿しました。最近またMCMCによるサンプリング熱が高まりつつあり、今度は多変数のメトロポリスヘイスティングに拡張できればと考えています。
さて、前回の実装では、事前分布の定義⇒尤度関数の定義⇒事後分布の定義⇒MCMCによるサンプリング、という流れで実装しました。ただ、MCMCのサンプリング方法は事後分布が変わってもコード自体に変化はないので毎回コードを書くのは正直言ってだるいです。事後分布を定義した関数を引数にとって自動的にMCMCを計算してくれるような関数があると便利な気がします。さらにいちいちオブジェクトを管理するのは大変なのでオブジェクト指向でクラスを定義してその中で簡潔できるといいですよね。
そこで今回は以前投稿した記事に投稿したMCMC実装部分をR6クラスと呼ばれるRで実現されているオブジェクト指向プログラミングクラスを用いて実装しなおしてみました。
目次
前回の投稿の復習
なるべくself-containedな記事にしたいので前回の投稿の内容を軽くここで書きます(詳しくは前回の投稿をご覧ください)。
問題設定
$y=3x+4$にノイズを乗せたデータに対して、傾き3が未知($y=ax+4$)だという体で事後分布により傾きを推定する、という設定です。
尤度関数とaに対する尤度関数は以下を仮定しました。
尤度関数
$$p(D|a)=\Pi_{i=1}^{N}\frac{1}{\sqrt{2\pi\sigma^2}}\exp\Big(-\frac{(y_{i}-(ax_{i}+4))^2}{2\sigma^2}\Big)$$
事前分布
$$ p(a)=\frac{1}{\sqrt{2\pi×2000000}}\exp\Big(-\frac{a^2}{2×2000000}\Big)$$
データ生成
以下はデータ生成のコードです。
############################ Data Generation ###################################
x <- seq( 0, 10, 0.1 )
y <- 3 * x + 4
y <- y + rnorm( length( x ), 0, 4 )
事後分布の定義
以下では事後分布(正確にいうと正規化はされていない)をパラメータ$a$(傾き)の関数として定義しています。
########################## Function Definition #################################
# likelihood function
like <- function( a ) {
sum <- 1
for( i in 1 : length( x ) ) {
sum <- sum * ( 1 / sqrt( 2 * pi * 4 ) * exp( - ( y[ i ] - a * x[ i ] - 4 )^2 / ( 2 * 4 ) ) )
}
return( sum )
}
# prior distribution
prio <- function( b ) {
1 / sqrt( 2 * pi * 2000000 ) * exp( - b ^ 2 / ( 2 * 2000000 ) )
}
# posterior distribution
dist <- function( c ) {
return( like( c ) * prio( c ) )
}
R6による実装
さてここからが本題です。前回ベタ打ちしたメトロポリスヘイスティングによるサンプリングをR6クラスで実装してみました。R6クラスによる実装はRでオブジェクト指向っぽくクラスを使ってみる(R6メソッド)を参考にさせていただきました。なお、前回のベタ打ちコードはこちらの記事には書かなかったのでもし必要があれば前回の記事をご覧ください。
早速ですが、R6クラスで実装した"MH"クラスのコードをこちらに書きました。基本的には事後分布とメトロポリスヘイスティングの初期値をコンストラクタの入力としました。そしてsample()というメソッドを実行するとサンプリングがsampleVecというフィールドに記録されていく仕組みです。またサンプル結果を簡単に可視化できると便利なので可視化用のvisualize()というメソッドを用意しました。showSummary()とshowParInfo()はそれぞれ事後分布とMCMCサンプリングに関わる情報を表示するメソッドです。
library( R6 )
MH <-
R6Class( "MH",
public = list(
posterior = NA, # posterior function
N.samp = 100000, # number of sampling
N.int = 100, # interval
burn = 100, # burnout
init = NA, # initial value
sampleVec = NA, # sampling with N.int interval after burnout
sampleVecAll = NA, # All of sampling from scratch
plots = list(), # list to store plots
initialize = function( posterior, init ) {
self$posterior <- posterior
self$init <- init
},
# method to run MCMC sampling
sampling = function(){
self$sampleVecAll <- self$init
for ( j in 1 : self$N.samp ) {
if( j %% ( self$N.samp %/% 10 ) == 0 ) {
cat( paste( ( 10 * j %/% ( self$N.samp %/% 10 ) ), "% Completed\n", sep = "" ) )
}
# previous sampling
x1 <- self$sampleVecAll[ j ]
# next candidate sampling
x2 <- rnorm( 1, x1, 1 )
# store sampling to samp following sampling role
alpha <- self$posterior( x2 ) / self$posterior( x1 )
if ( alpha >= 1 ) {
self$sampleVecAll <- c( self$sampleVecAll, x2 )
} else {
p <- runif( 1, 0, 1 )
if ( p < alpha ) {
self$sampleVecAll <- c( self$sampleVecAll, x2 )
} else {
self$sampleVecAll <- c( self$sampleVecAll, x1 )
}
}
# store sampling to sampleVec if satisfies interval condition
if ( j >= self$burn ) {
if ( j %% self$N.int == 0 ) {
self$sampleVec <- c( self$sampleVec, self$sampleVecAll[ j + 1 ] )
}
}
}
self$sampleVec <- self$sampleVec[ - 1 ]
self$plots <- list(
function() plot( self$sampleVecAll, ylab = "Sampling", xlab = "Iteration", main = "all of sampling" ),
function() plot( self$sampleVec, ylab = "Sampling", xlab = "Iteration", main = "sampling after burnout with interval" ),
function() hist( self$sampleVec, main = "Histogram of Sampling", xlab = "Sampling" ),
function() acf( self$sampleVec, plot = TRUE, main = "sampling after burnout with interval" )
)
},
# method to visualize sampling
visualize = function() {
if( length( self$sampleVecAll ) == 1 ){
stop( "please run sampling() beforehand" )
} else {
for( i in 1 : length( self$plots ) ) {
self$plots[[ i ]]()
if( i < length( self$plots ) ) {
readline( prompt = "次のプロットを出力するにはEnterを押してください" )
}
}
}
},
# method to show mean and variance of posterior distribution
showSummary = function() {
cat( "summary of posterior distribution is as follows:\n" )
cat( "[1] mean: ", mean( self$sampleVec ), "\n" )
cat( "[2] variance: ", var( self$sampleVec ), "\n" )
},
# method to show the general information on MCMC sampling
showParInfo = function() {
cat( "basic information on MCMC sampling is as follows:\n" )
cat( paste( "[1] number of sampling: ", self$N.samp, "\n" ) )
cat( paste( "[2] interval of sampling: ", self$N.int, "\n" ) )
cat( paste( "[3] burnout: ", self$burn, "\n" ) )
}
)
)
実行結果
先ほど定義して事後分布の関数(dist関数)を用いて実際にMHクラスを実行してみます。
> MCMC <- MH$new( dist, 2)
> MCMC$sampling()
[1] "10% Completed"
[1] "20% Completed"
[1] "30% Completed"
[1] "40% Completed"
[1] "50% Completed"
[1] "60% Completed"
[1] "70% Completed"
[1] "80% Completed"
[1] "90% Completed"
[1] "100% Completed"
サンプリング経過はこのようにパーセンテージで表示するようにしました。
以下は事後分布から推定された$a$の値です。
> MCMC$showSummary()
summary of posterior distribution is as follows:
[1] mean: 2.951999
[2] variance: 0.00113598
およそ$a=3$となっておりうまく推定されていることが分かります。
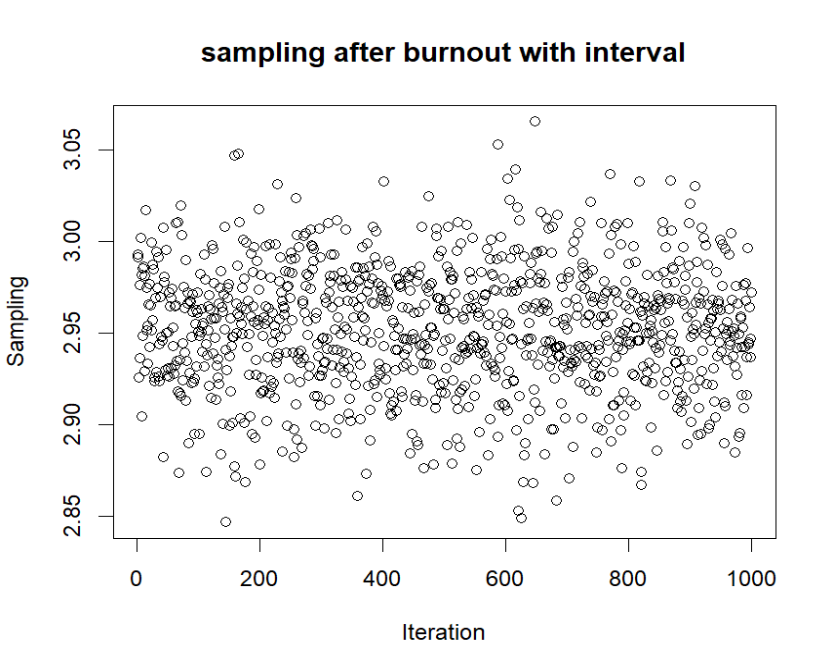
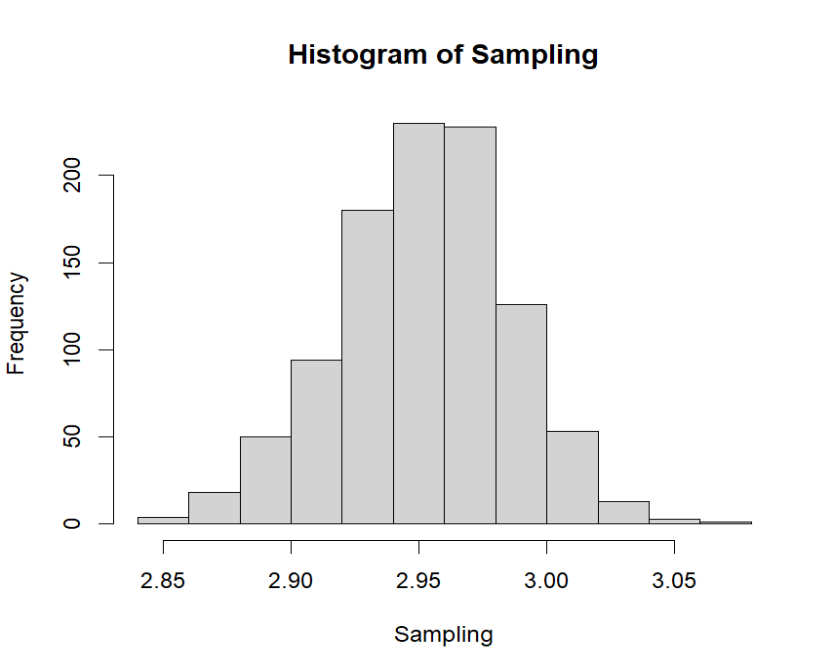
次が可視化を担当するメソッドです。Enterを打つことで次のプロットに移行するようしました。一つ目がすべてのサンプリング、二つ目が100回目以降のサンプリングを100サンプルごとに表示した結果です。三つ目は二つ目をヒストグラムで表したもの、四つ目は自己相関係数です。
> MCMC$visualize()
次のプロットを出力するにはEnterを押してください
次のプロットを出力するにはEnterを押してください
次のプロットを出力するにはEnterを押してください
最後にメトロポリスヘイスティングのサンプリングに関する情報です。フィールドで定義した方が良かったかもしれませんが、メソッドで定義してみました。意外と必要かと思っています。
> MCMC$showParInfo()
basic information on MCMC sampling is as follows:
[1] number of sampling: 1e+05
[2] interval of sampling: 100
[3] burnout: 100
まとめ
ということで今回はR6を使ってメトロポリスヘイスティングのクラスを作成してみました。多変数にのメトロポリスヘイスティングができるように拡張するのもやりたいですが、今回手で定義した事後分布も事前分布と尤度関数から自動的に作ってくれるように拡張してみてもいいなと思いました。
メトロポリスヘイスティングのパッケージは世の中にたくさんあるわけですがやっぱり実際に手で実装してみると理解度が一気に上がります。今回の記事が何らかの参考になれば幸いです。