遅延セグ木のイメージが掴めずこれまで2回くらい挫折してきたのでそろそろ本気で理解しようと思う。
ここではまずは遷移のお気持ちだけ。コードは別途記事書く。
対象
- セグメント木の一点更新/区間取得の処理を理解している。
- 遅延セグ木に挫折している。
(遅延しない普通の)セグメント木
本題ではない ので軽めに記載。
一応、セグ木といってもいくつかの流派みたいなものがあって、0/1-indexedとか再帰/非再帰とか2冪どうのとかあるので一度イメージをここであわせておく。なお、今回想定する遅延セグ木の完成形は1-indexed/非再起/2冪にしようと思う。
そもそもセグ木とは?
要素数Nの数列に対し、一点更新および任意区間の演算結果をO(logN)で処理できるデータ構造。
具体的にはこういう問題に対し回答できるデータ構造。
https://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=DSL_2_A&lang=ja
以下要約。
要素数Nの数列Aが与えられ、全ての要素は2^31-1である。
次の2種類のクエリがQ個与えられる。update(i, x): i項目をxに変更する。
find(s, t): s項目からt項目までの最小値を出力する。各findクエリについて、最小値を出力せよ。
制約: 1 ≤ N ≤ 10^5 , 1 ≤ Q ≤ 10^5
仕組み
- ノード数(2N - 1)の二分木(2冪である必要はない) ノード
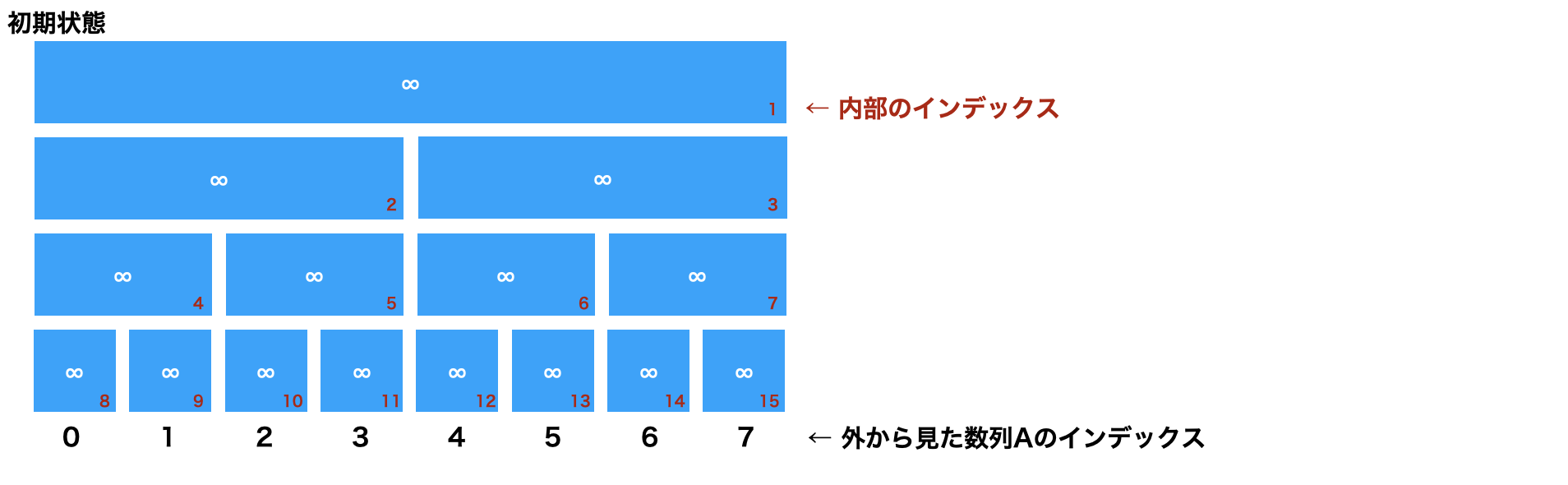
i(1≦i≦(N-1))はノード2iとノード2i+1の演算結果を持つ。ノードi(N≦i≦(2N-1))はセグ木の最下層で実際の値を持っている。 - index 0は使わない方が楽なので内部では1-indexedとし関数のインターフェースで0-indexedっぽくしたらいい。
- 始めに全てのノードを単位元で詰めておく。 (単位元 : 演算結果に影響を与えないもの的なやつ。 加算処理なら0。最小値処理なら無限。)
セグ木のお気持ち
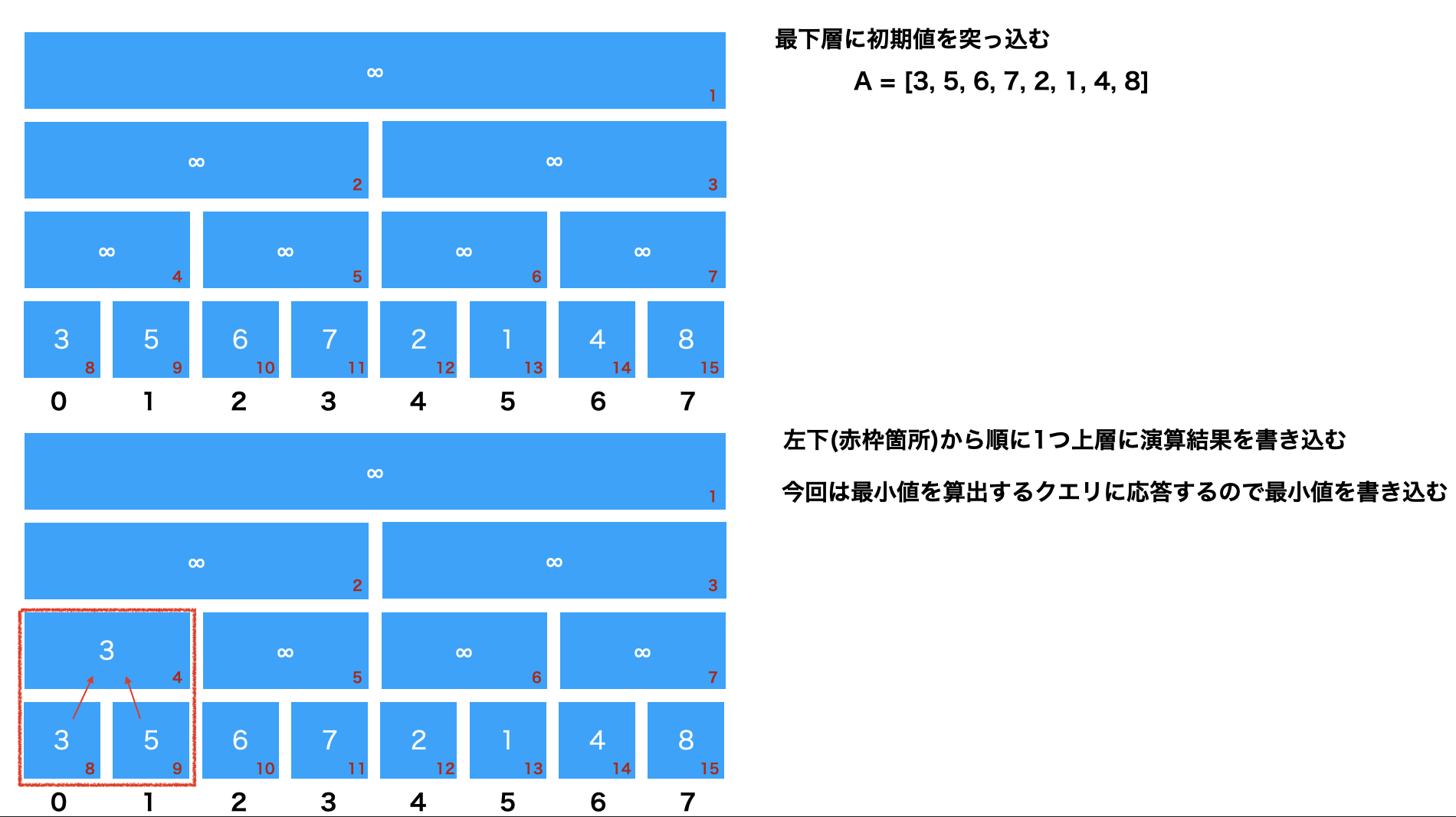
以下、A = [3,5,6,7,2,1,4,8]としてセグ木を構築する。
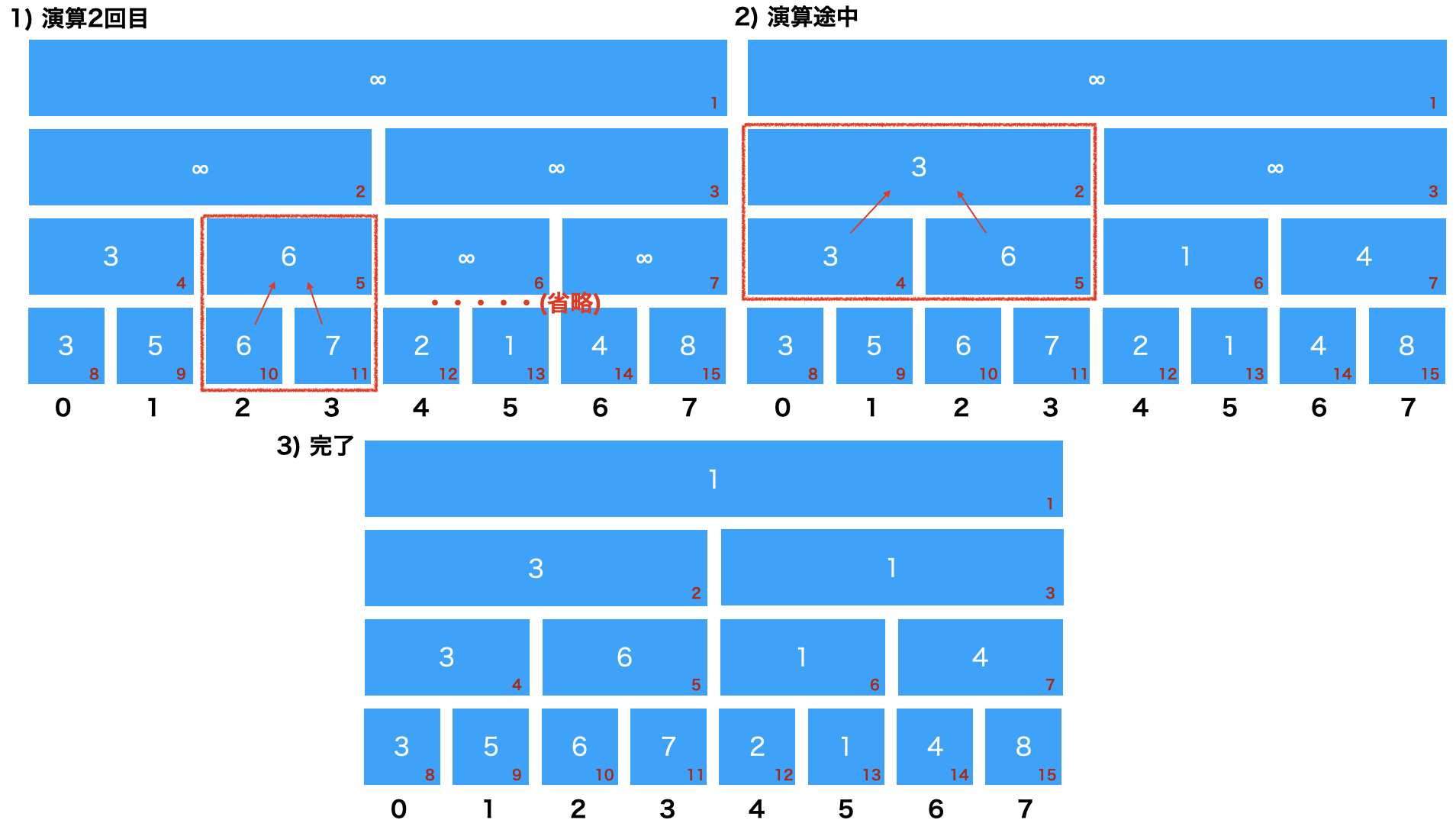
左下から順に下層のノードの演算結果を格納していく。
これを繰り返し、最後(ノード1)まで埋める。
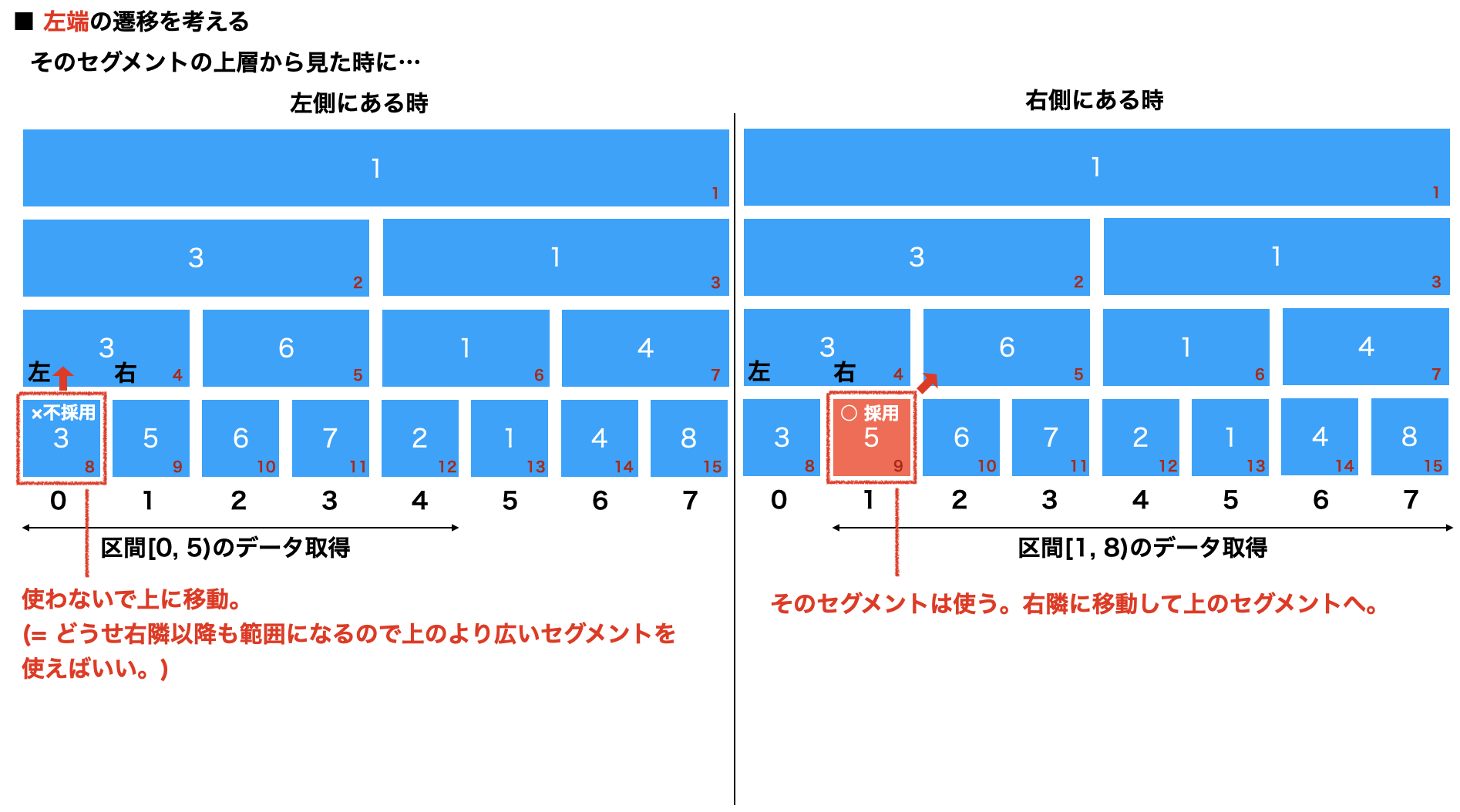
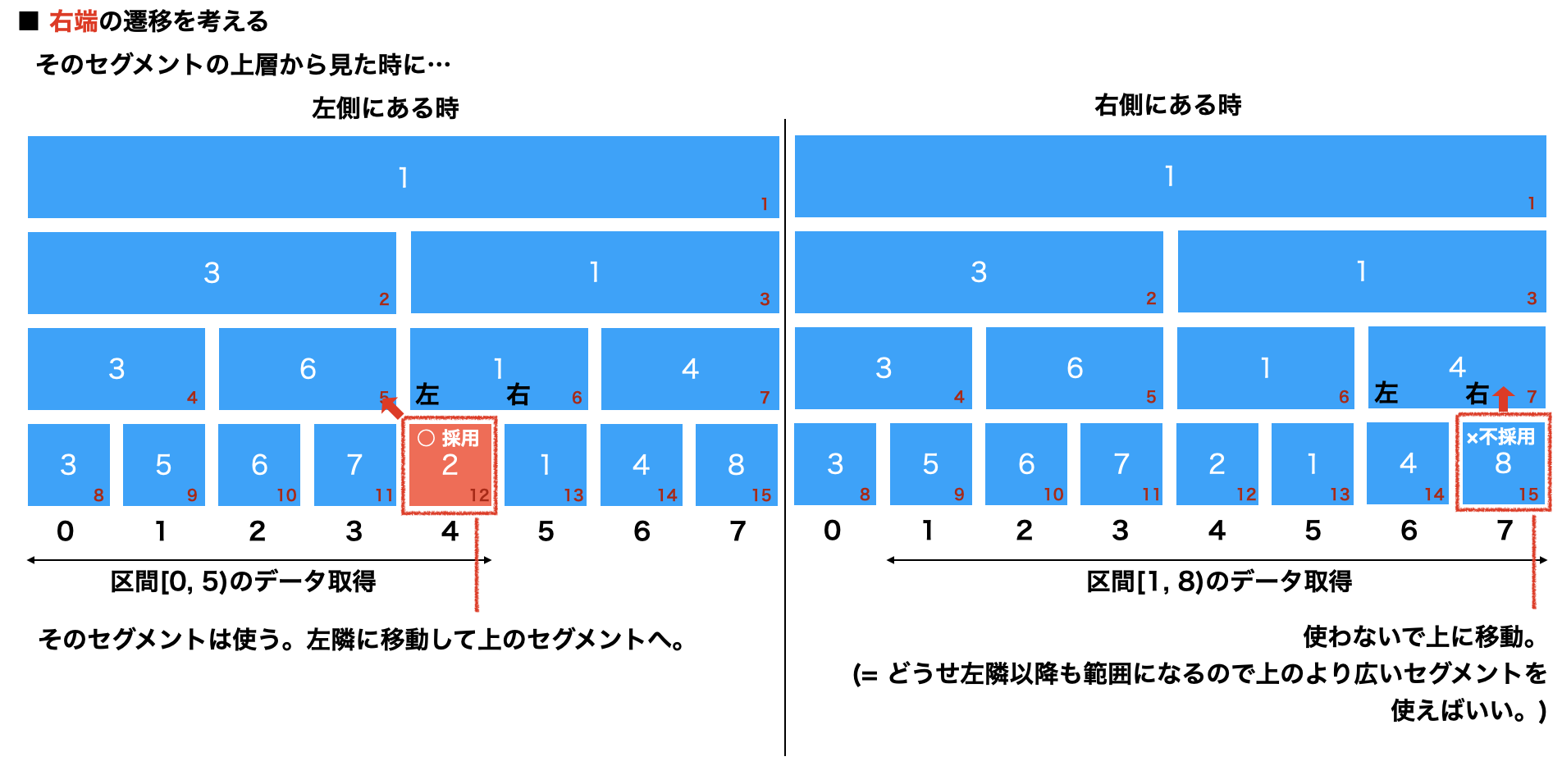
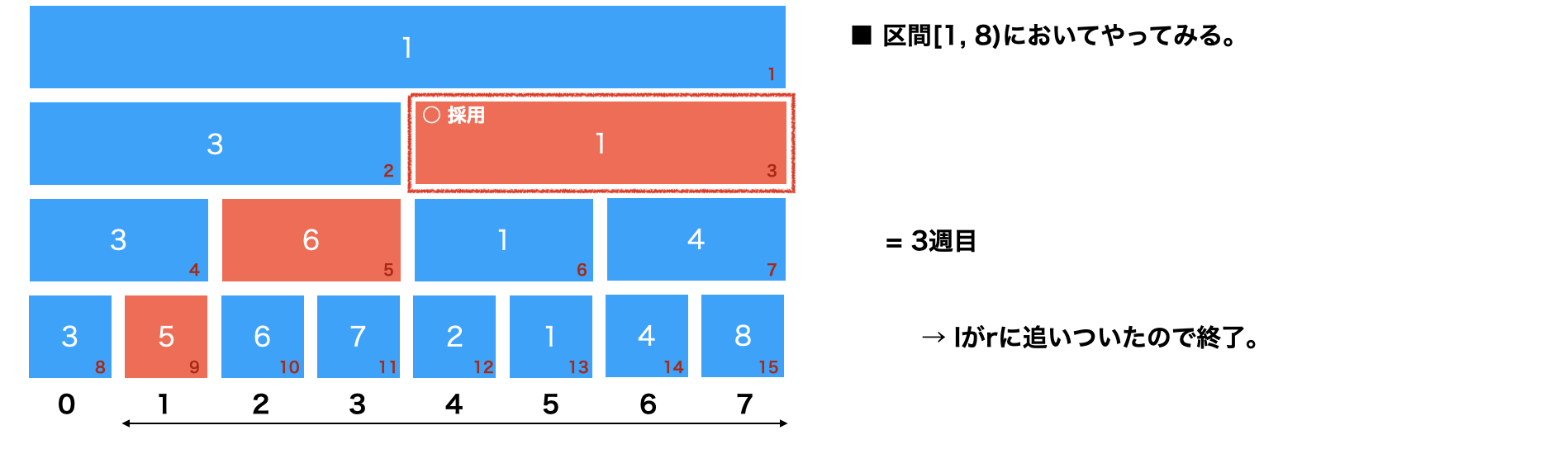
区間の演算結果の取得には以下のように影響範囲をできるだけ大きなブロックを利用して結果を算出する。
最下層の両端から交互に見ていく。(セグ木自体は今回の本題じゃないのでやや雑な絵で)
これを左右交互に繰り返す少しずつ両端を中央に寄せていく。
こんな感じで取得範囲が分かれば端から計算していくだけ。
遅延セグメント木
本題はこっち。
セグ木は区間処理できるわけだが、区間更新がある問題にやや難あり。
区間更新を全て一点更新と見做して処理するとTLEしてしまう。要は以下のような問題に対応できない。
例題
要素数Nの数列Aが与えられ、全ての要素は2^31-1である。
次の2種類のクエリがQ個与えられる。update(s, t, x): s項目からt項目までをxに変更する。
find(s, t): s項目からt項目までの最小値を出力する。各findクエリについて、最小値を出力せよ。
制約: 1 ≤ N ≤ 10^5 , 1 ≤ Q ≤ 10^5
ここで、出力処理が要求されるまで更新を遅延し、必要になったらまとめて演算しようぜってのが遅延セグ木の考え方。通常の値配列と遅延評価用に保持しておく配列があって云々って説明はたくさん見てきたけど動きがいまいち理解できなかったので可視化する。
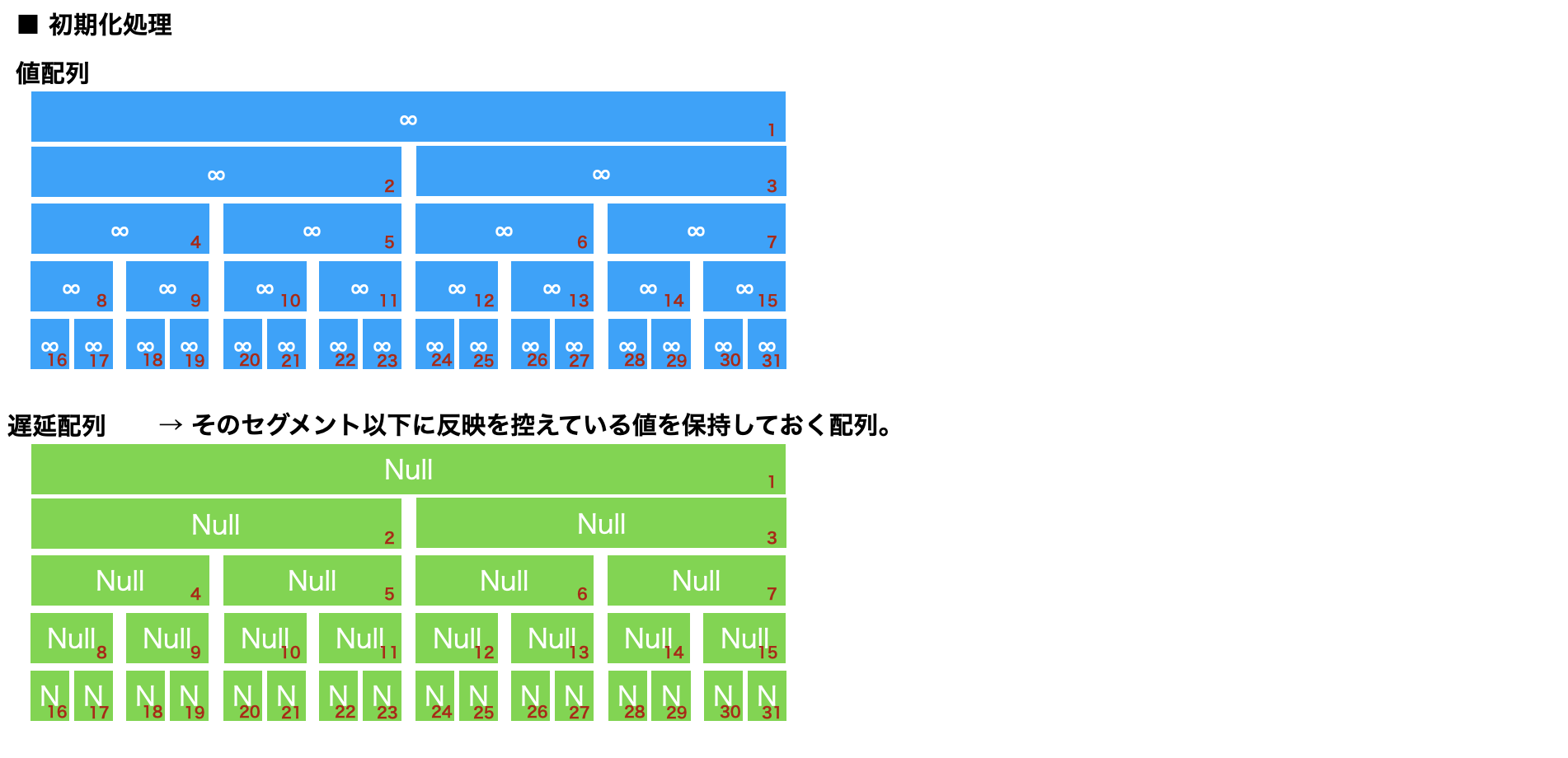
値配列はモノイドで初期化し、遅延配列はNullで初期化しておく。0だと0に更新する処理と区別がつかない。
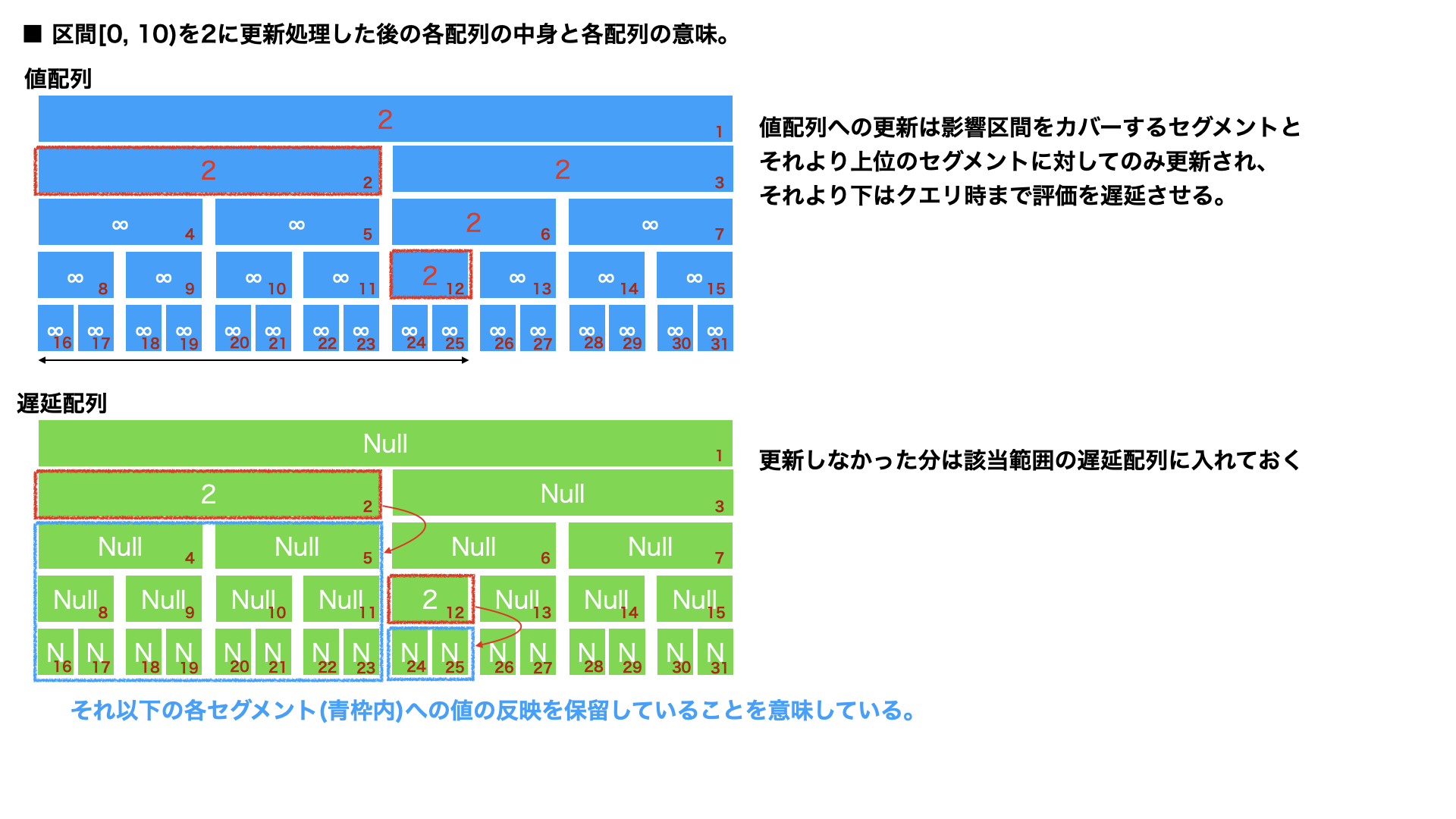
この2つの配列はそれぞれ以下のように解釈する。例えば図は区間[0,10)を2で更新した後の図。
値配列はその区間の演算結果の値を示す。そのセグメントよりも上に対して更新していく。
一方で、遅延配列はその区間(そのセグメント自体は含まない)より下のセグメントにまだ更新していないことを示す。なので更新処理は下に向かって進める。
遅延セグ木のお気持ち
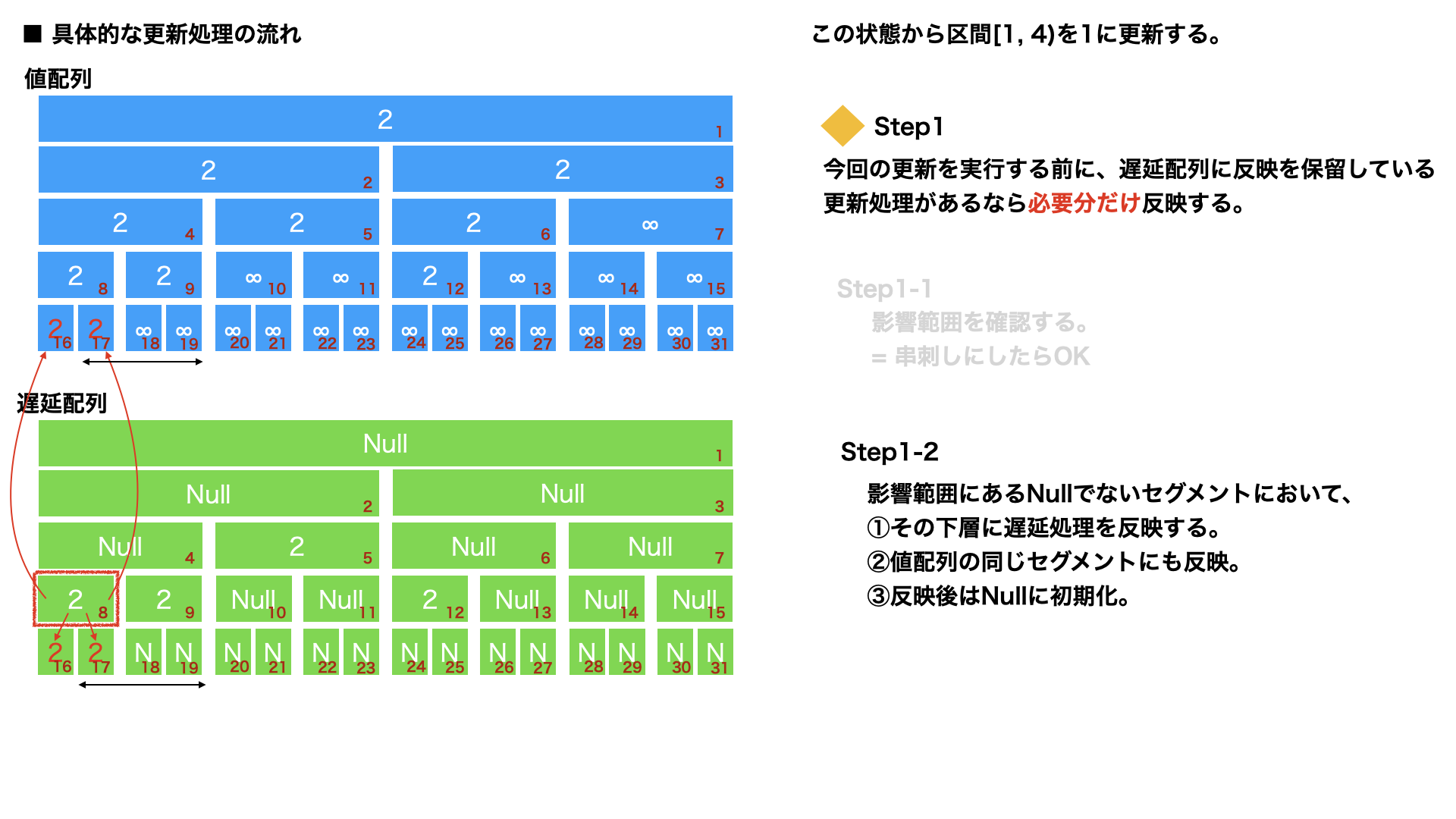
区間更新 : Step1
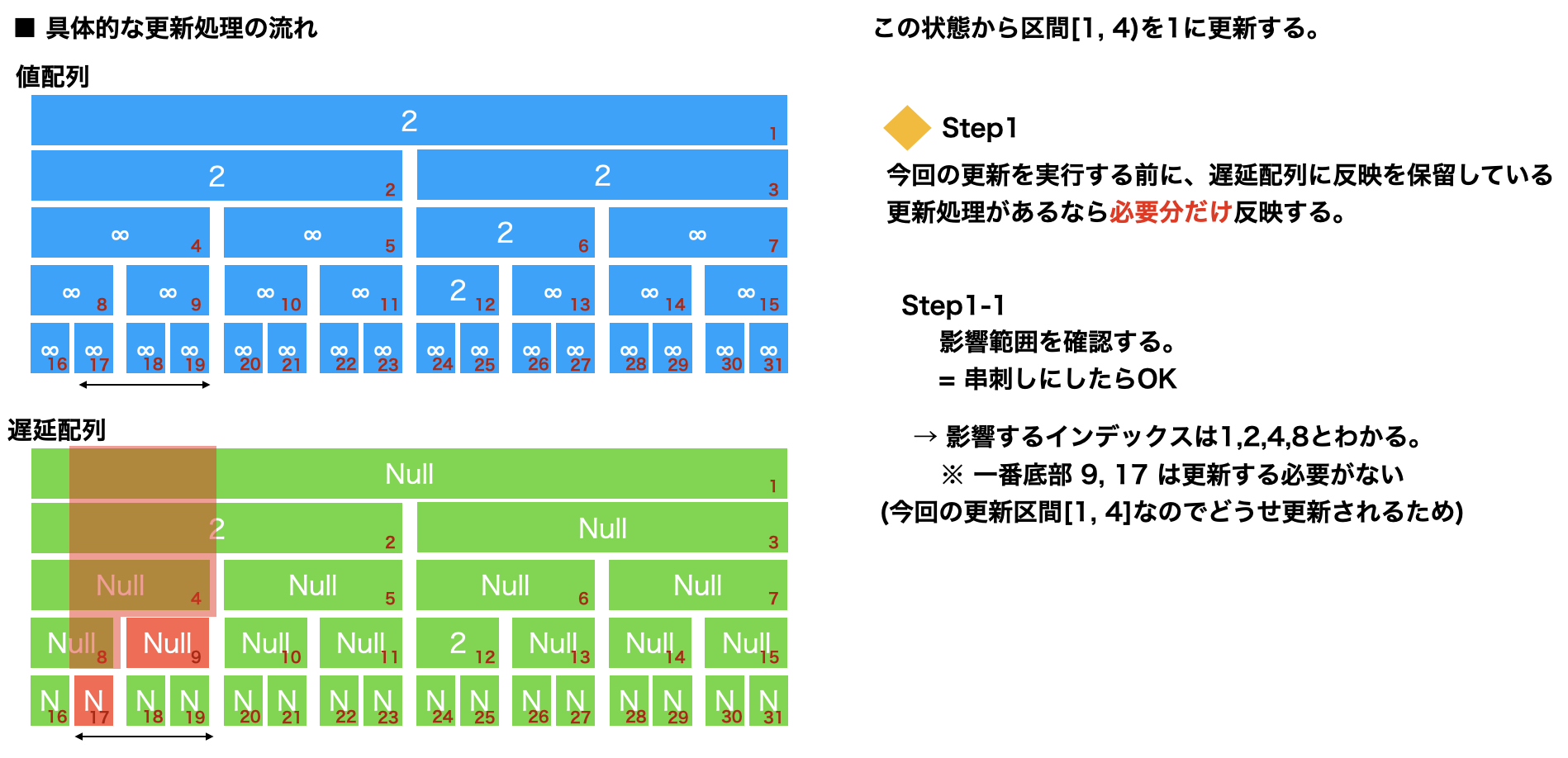
上の状態を元に、以下この遅延セグ木の更新の様子を確認する。
区間[1,4)を更新する場合、以下のようになる。
図中に記載の通り、
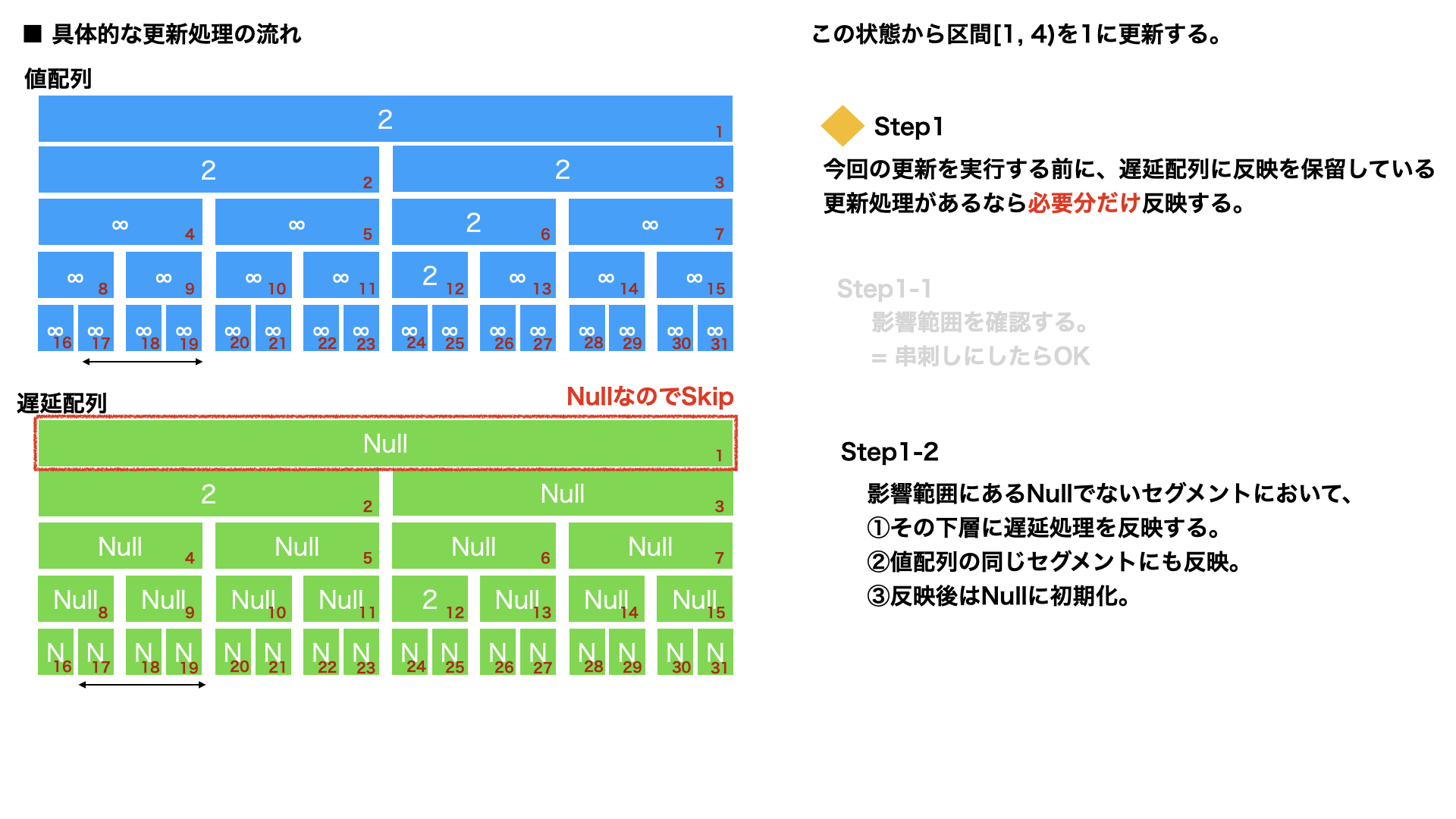
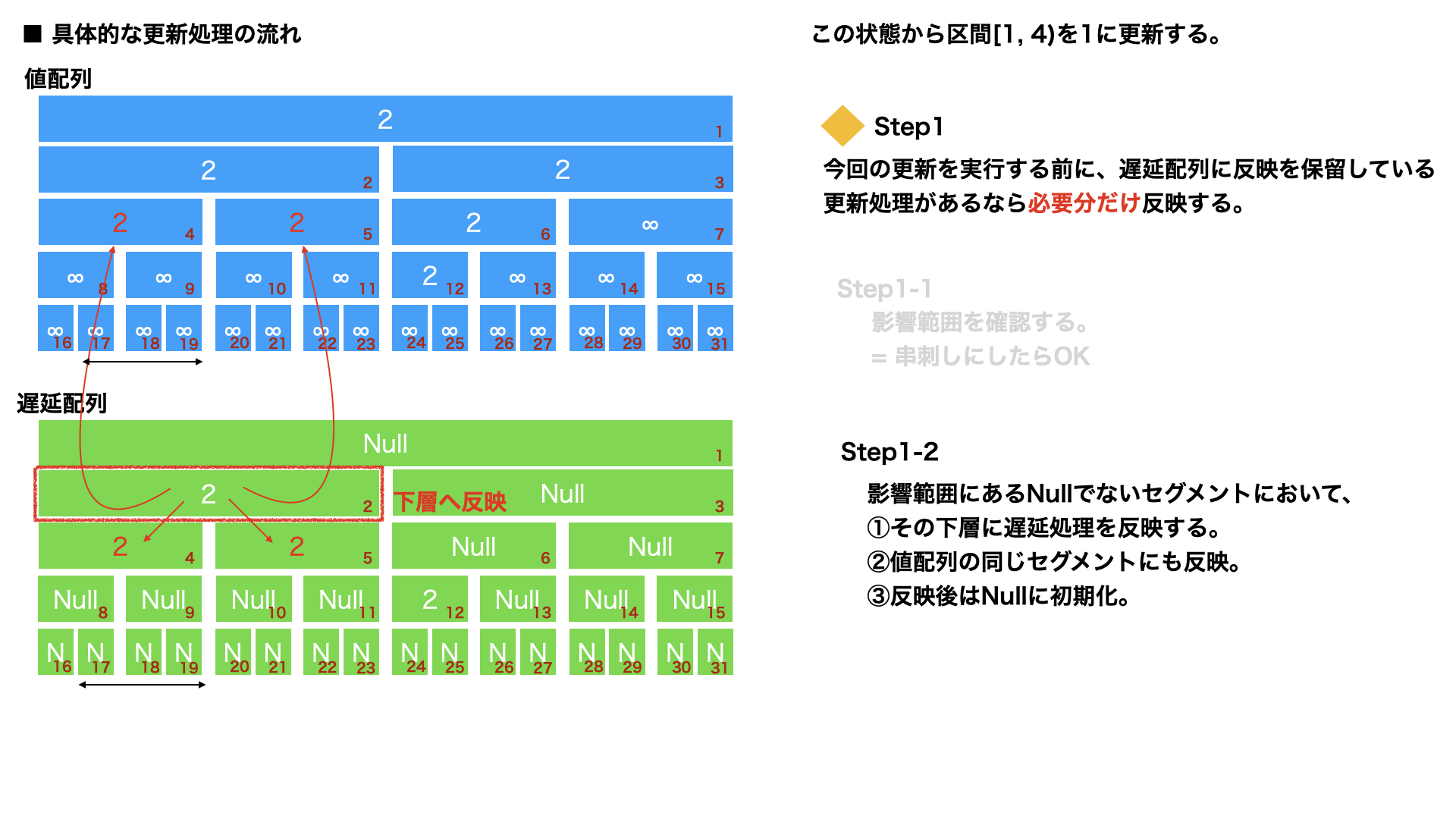
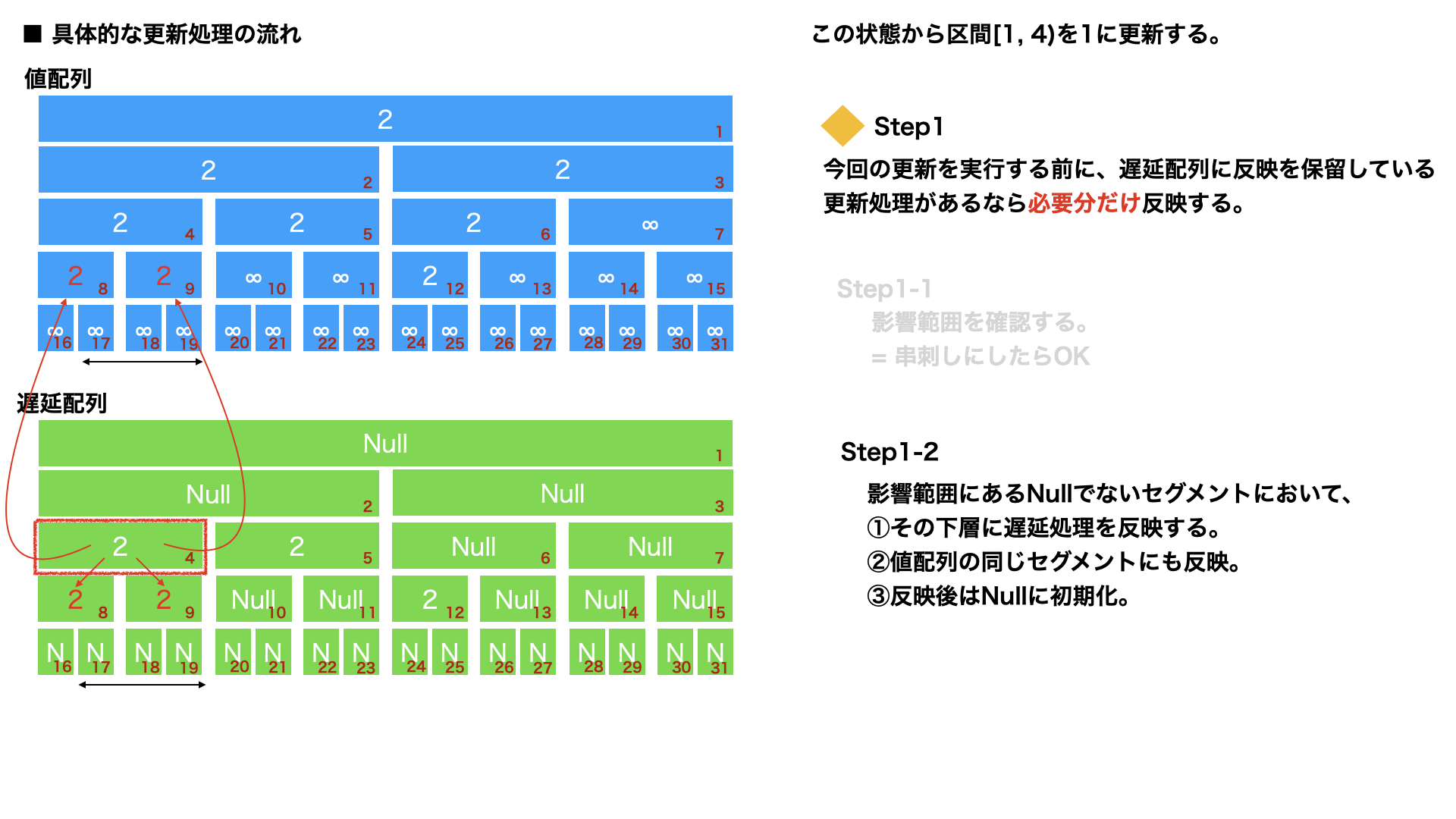
影響範囲にあるNullでない遅延配列のセグメントにおいて、
①その下層に遅延処理を反映する。
②値配列の同じセグメントにも反映。
③反映後はNullに初期化。
この処理を繰り返すことで下に向かって必要分だけ遅延処理を反映できる。
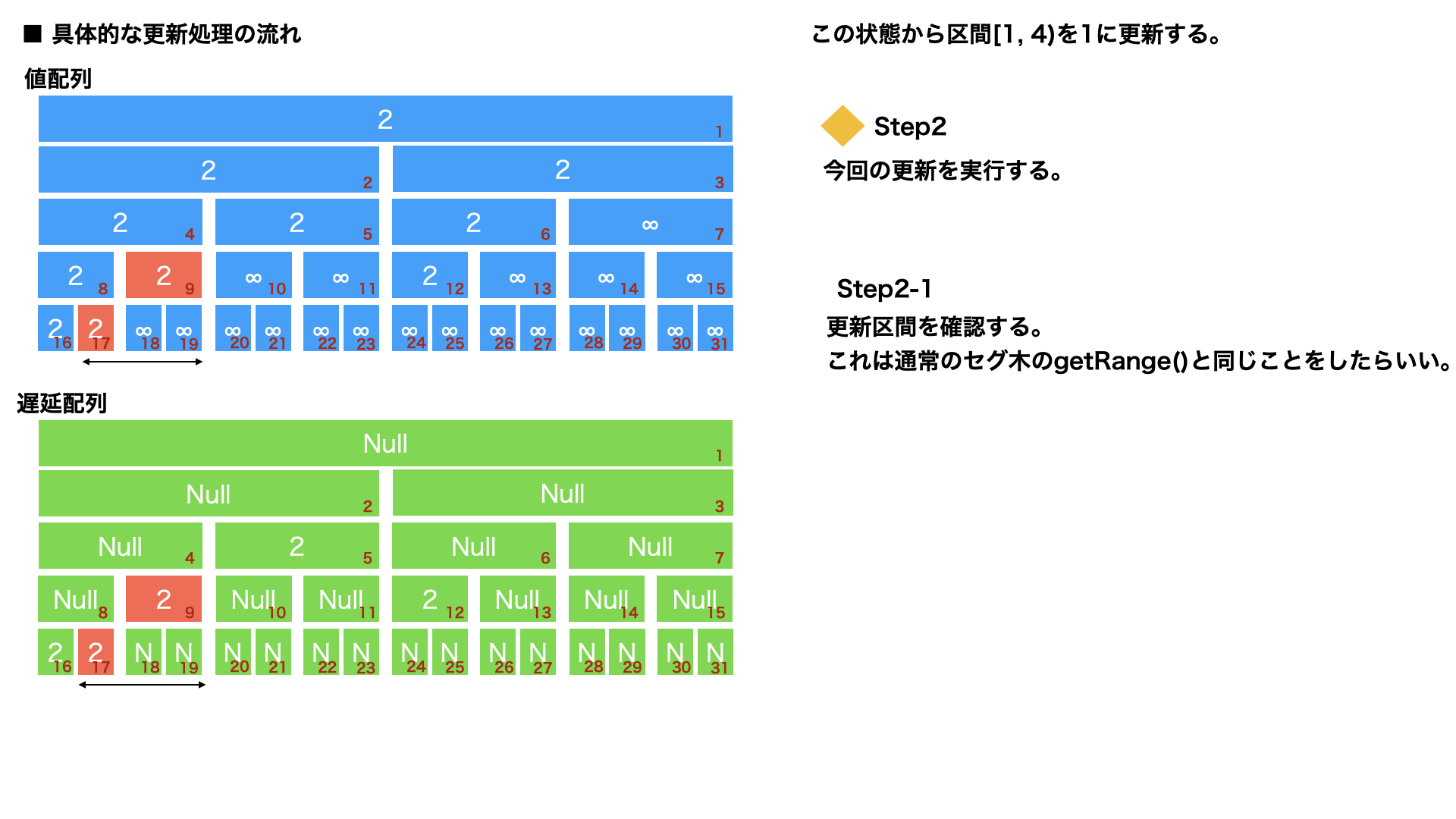
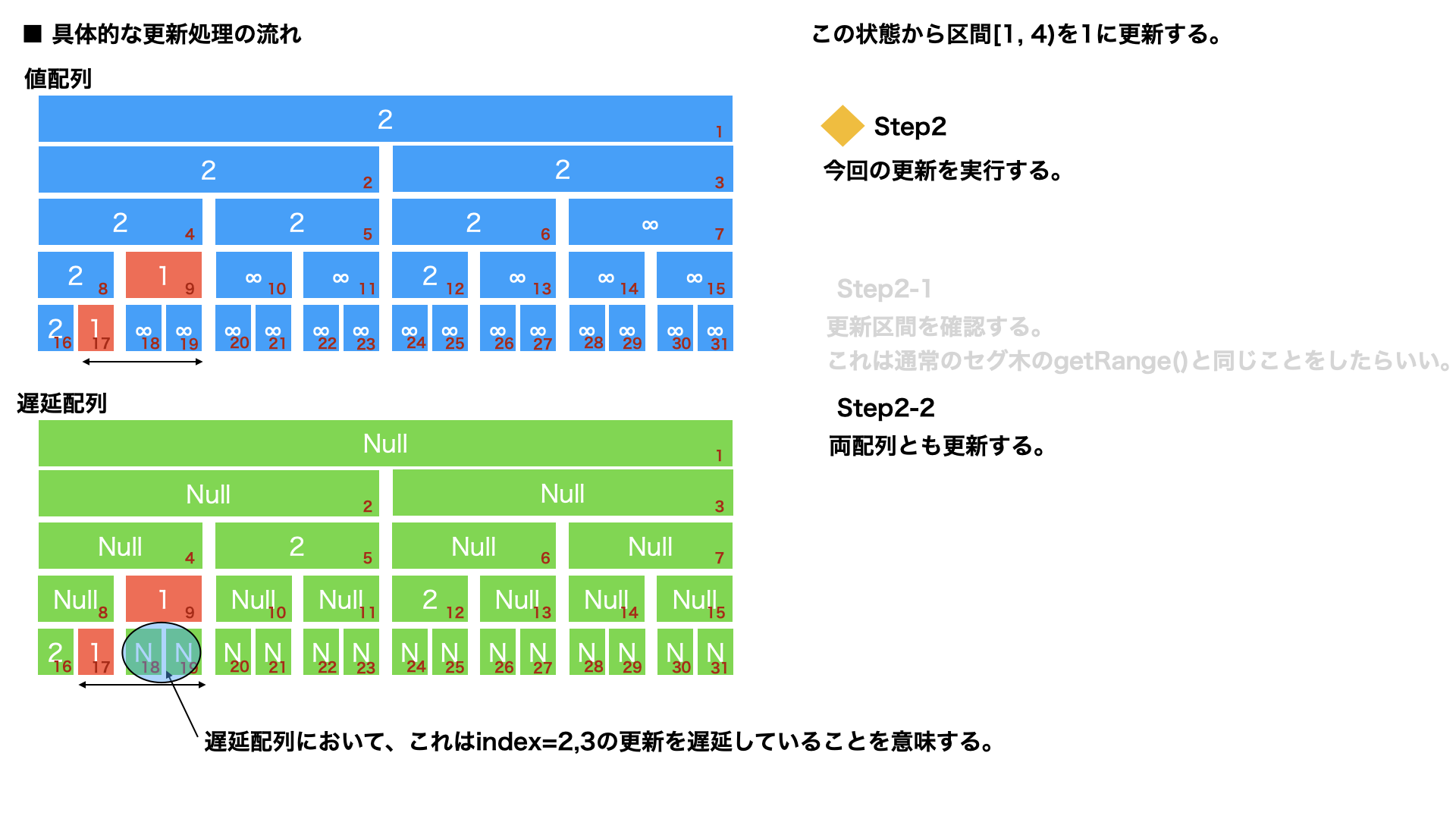
区間更新 : Step2
次に、更新範囲に今回の更新処理1に更新する行為を行う。
これは一般のセグ木で最大のカバー範囲を求めて値を返すクエリと同じことをすればよい。
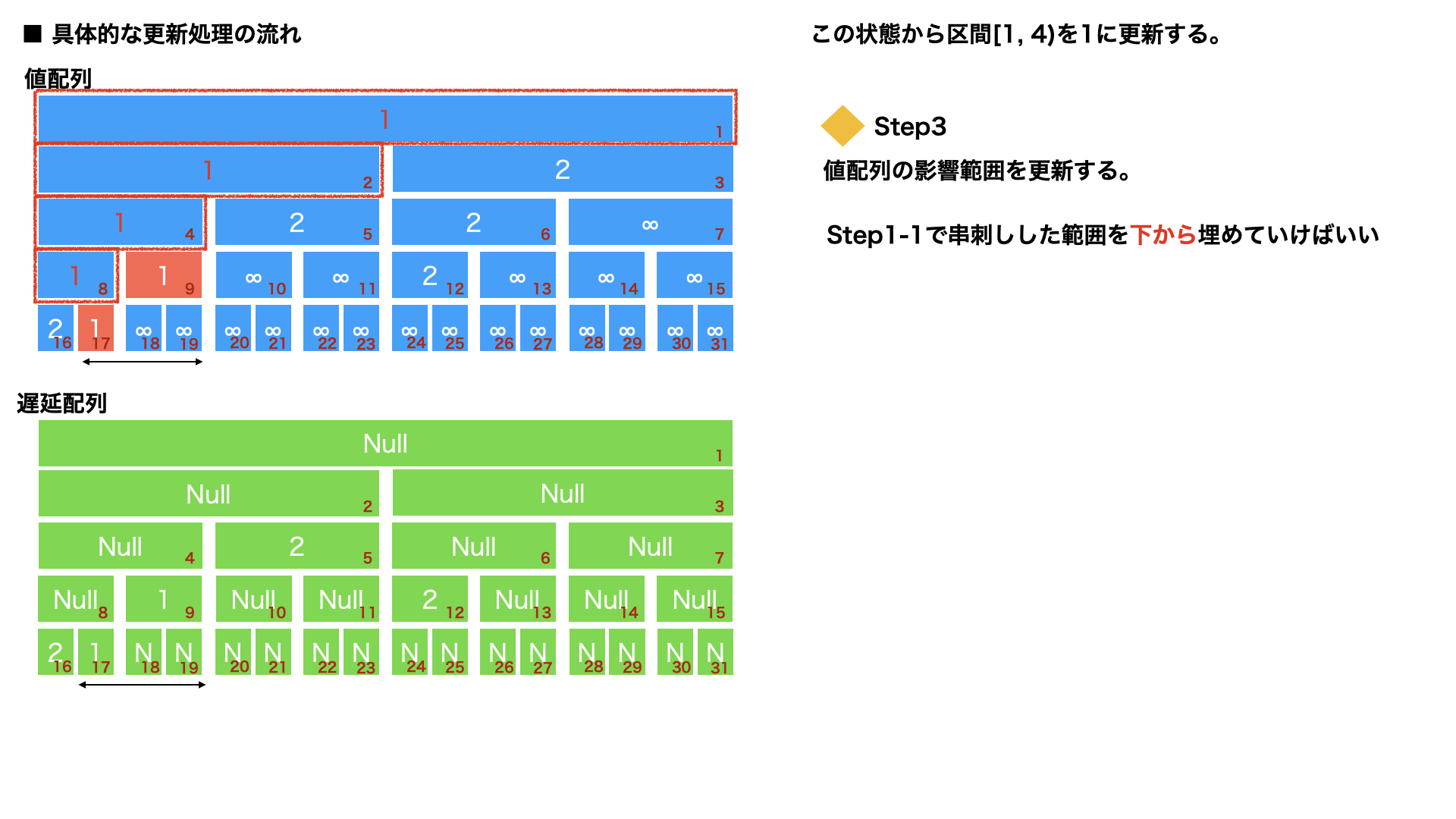
区間更新 : Step3
値配列を上に向かって更新していく。これはStep1-1で算出した範囲を逆から辿っていけばいい。
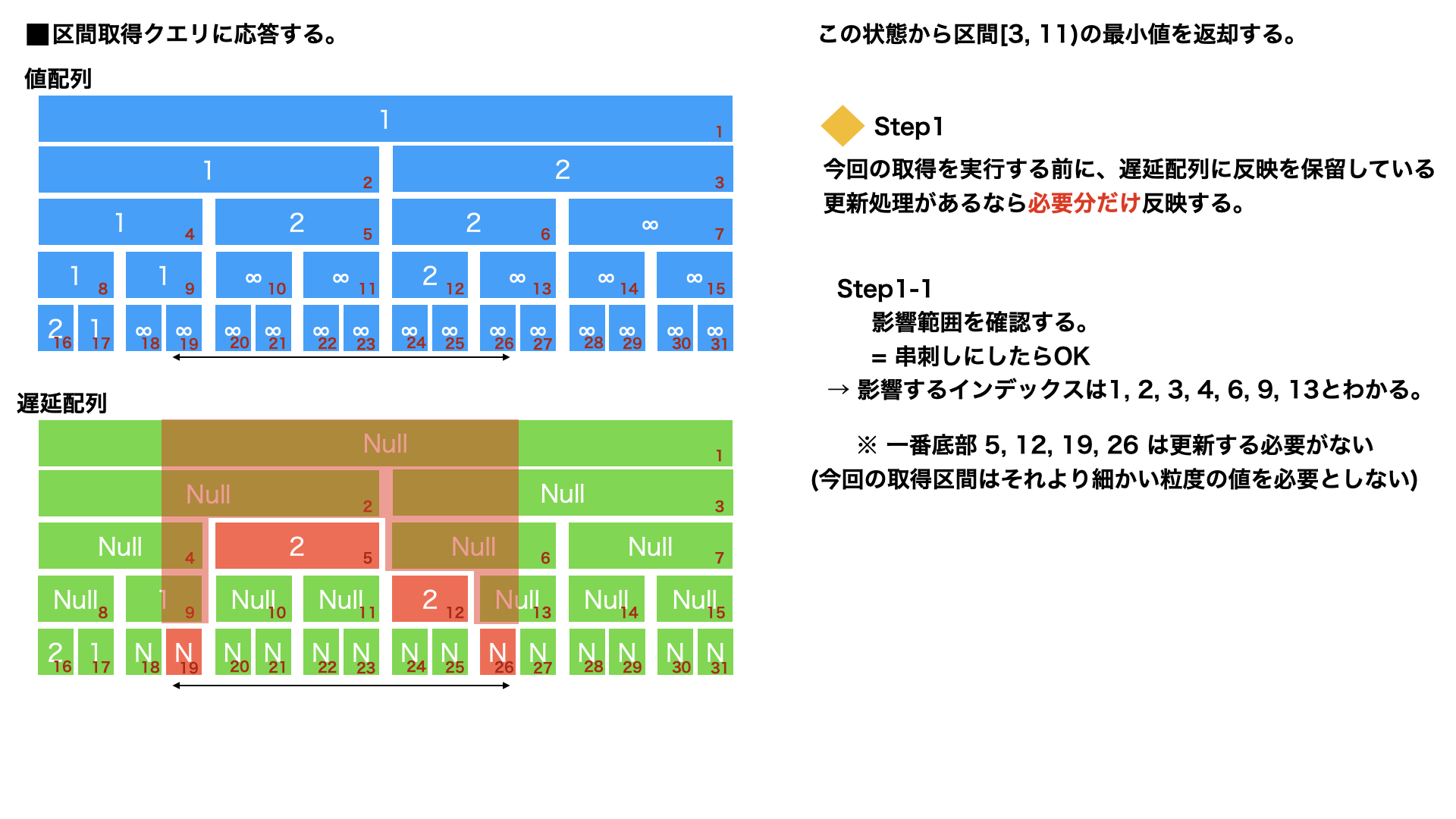
区間取得 : Step1
ここまで理解できると取得は結構楽。更新のStep1,2と同じようなことをするだけ。
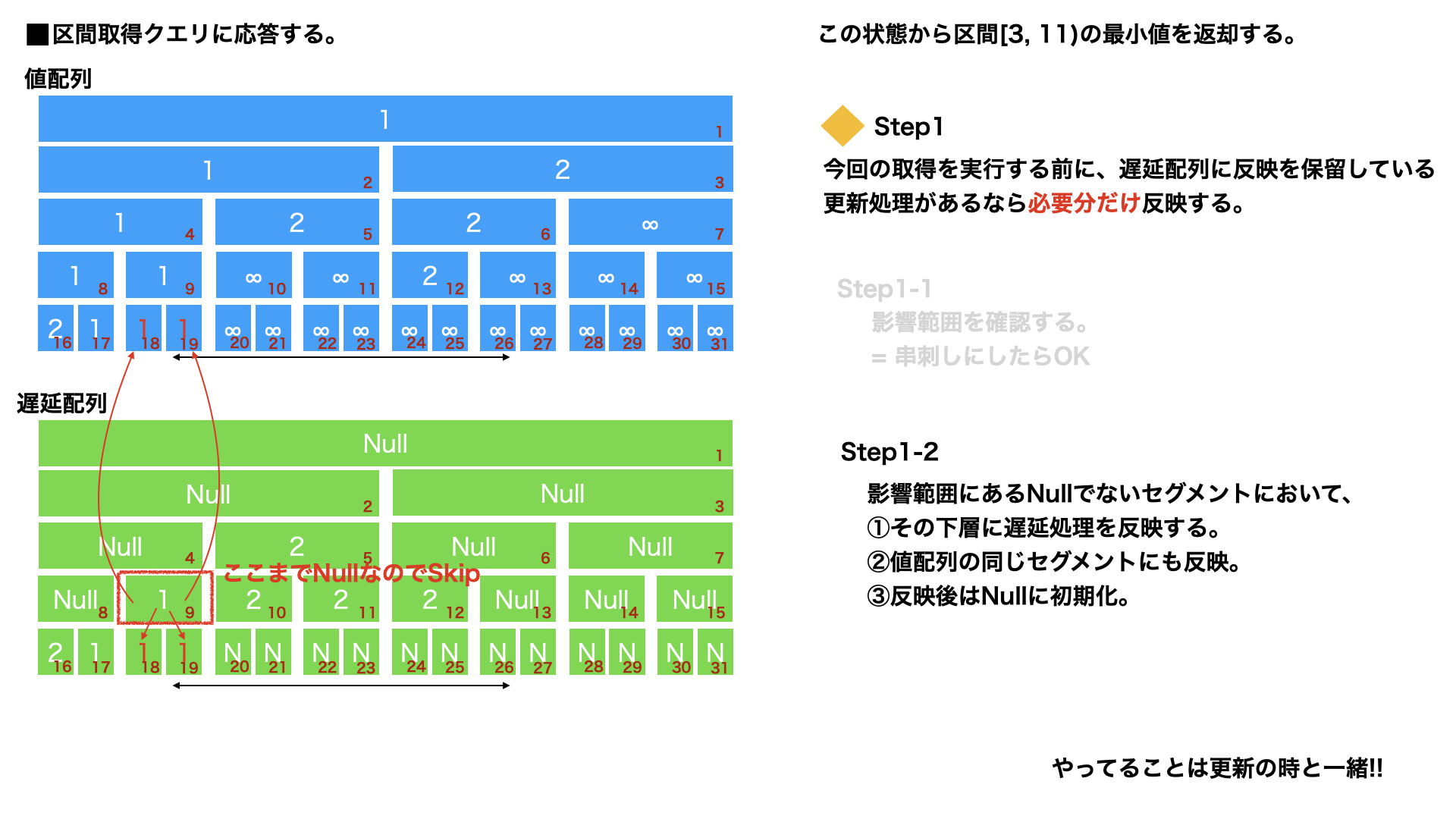
まずは、遅延されている処理があるなら反映する。
先ほど同様、串刺しになる範囲を求め、Nullじゃないなら遅延評価を行う。
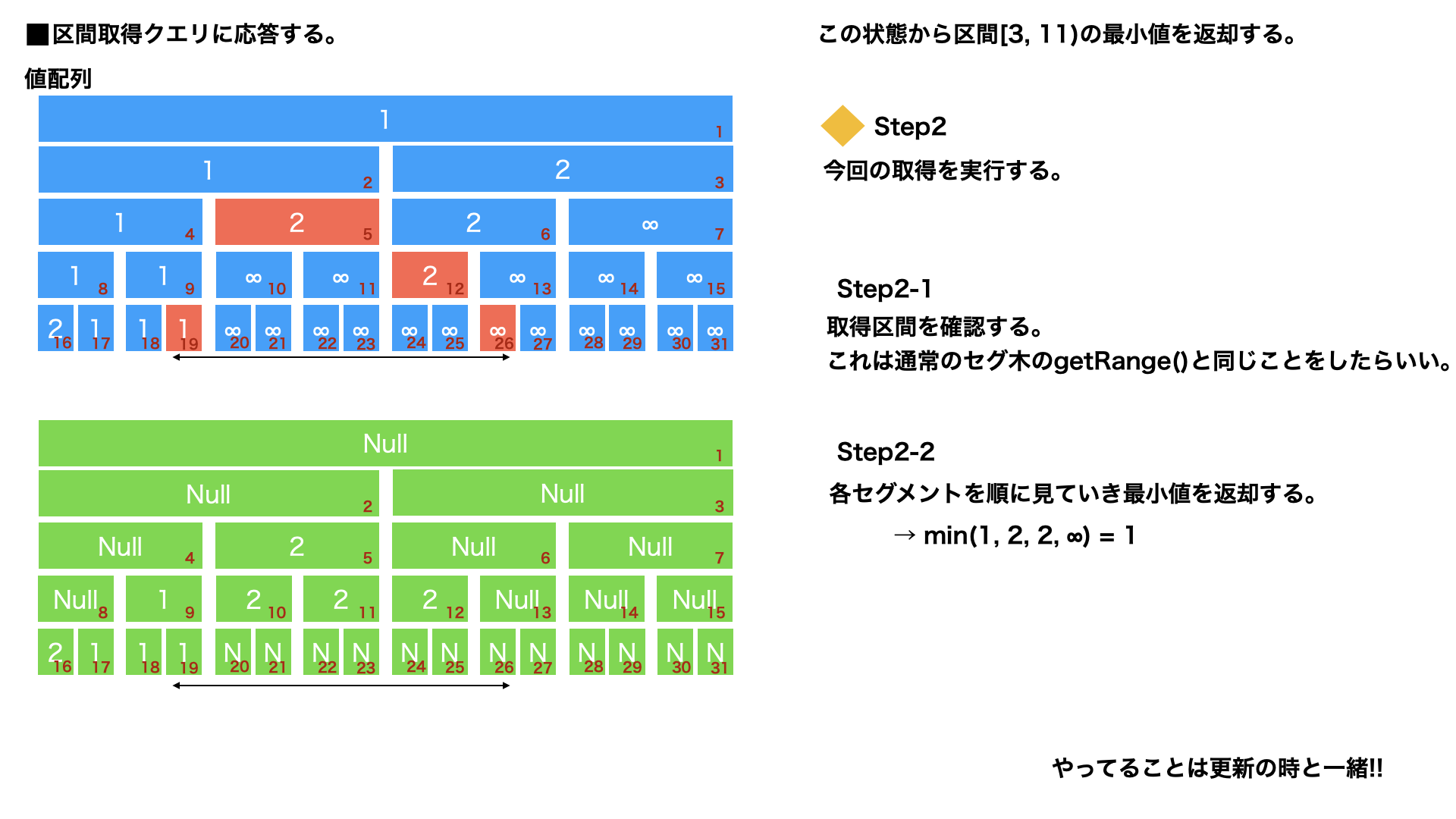
区間取得 : Step2
完了したら取得。これはほぼさっきまでと一緒。できるだけでかい範囲のセグメントを使用して演算結果を返す。
まとめ
特にまとめることはなかった。
明日遅延評価セグ木の実装についてまとめるつもり。