以下のイメージをコード化する。
まずは区間最小を計算するセグ木を作り、あとから任意の演算に対応できるように拡張する。
区間更新/区間最小値取得 遅延セグ木
検証する問題
骨格を作る
まずは遅延セグ木が内部で必要とするデータ構造を用意する。
class LazySegTree:
def __init__(self, unit: int, bottomLen: int, func: "function"):
self.unit = unit # 単位元
self.func = func # 関数
self.bottomLen = bottomLen # 最下層の配列長
self.offset = self.bottomLen # 最下層の先頭インデックスに合わせるためのオフセット
self.segLen = self.bottomLen * 2 # セグ木全体の配列長
self.tree = [unit] * self.segLen # 値配列
self.lazy = [None] * self.segLen # 遅延配列
初期化
セグ木の時はそのまま最上段まで演算し構築したが、遅延セグ木ではそれ自体も遅延できるので必要な時に伝播させる。
セグ木同様、最下層に初期値を入れたら一度上まで構築する。
これ省略できると思っていたが初期化直後に更新クエリがなく取得クエリがきた場合に誤った答えを返すのでNG。
def build(self, seq):
# 最下段の初期化
for i, x in enumerate(seq, self.offset):
self.value[i] = x
self.lazy[i] = x
for i in range(self.offset - 1, 0, -1):
self.value[i] = min(self.value[i << 1], self.value[i << 1 | 1])
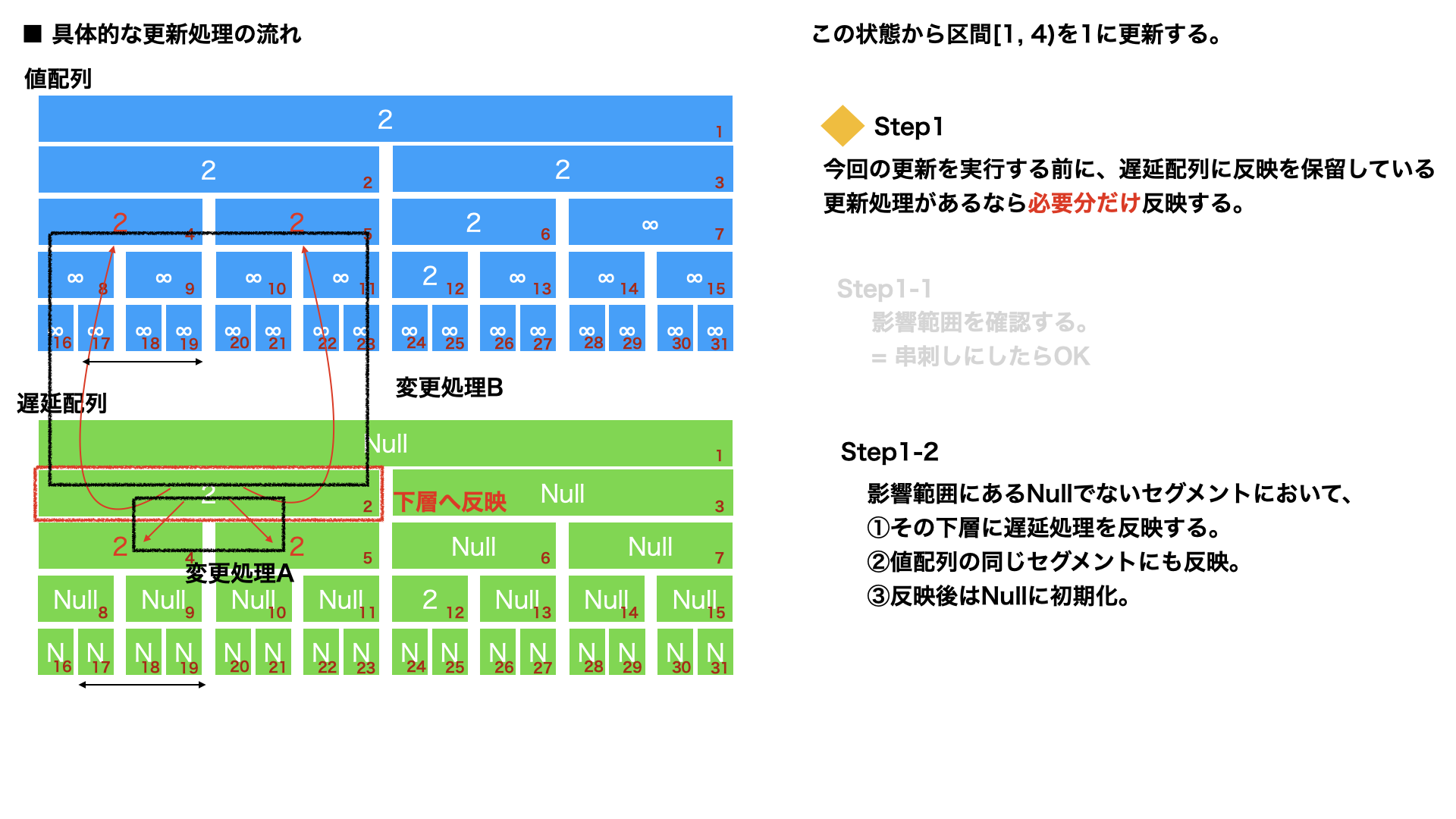
区間更新 : Step1
区間更新 : Step1-1
必要箇所だけ伝播させるためその操作対象のインデックスのリストを生成する。
以下の記事で紹介してくれている方法が参考になる。
def _gindex(self, l, r):
lm = (l // (l & -l)) >> 1 # lから遡上していき、右側に位置するまで進む。右側に位置したセグメントの1つ上を新たにlとして更新し、そこまでは伝播必要といえる。
rm = (r // (r & -r)) >> 1 # lから遡上していき、右側に位置するまで進む。右側に位置したセグメントの1つ上を新たにrとして更新し、そこまでは伝播必要といえる。
while l < r:
if r <= rm:
yield r
if l <= lm:
yield l
l >>= 1
r >>= 1
while l:
yield l
l >>= 1
区間更新 : Step1-2
def _propagateAt(self, idx: int):
# Nullでないセグメントにおいて、
if self.lazy[idx] is None:
return
# ①その下層に遅延処理を反映する。
self.lazy[idx << 1] = self.lazy[idx]
self.lazy[idx << 1 | 1] = self.lazy[idx]
# ②値配列の同じセグメントにも反映。
self.value[idx << 1] = self.lazy[idx]
self.value[idx << 1 | 1] = self.lazy[idx]
# ③反映後はNullに初期化。
self.lazy[idx] = None
return
この関数を_gindex()で生成する範囲を上から順にコールしていく。
# 更新区間に関係するlazyを全て子に伝播させる。
for idx in reversed(list(self._gindex(l, r))):
self._propagateAt(idx)
区間更新 : Step2
通常のセグ木で範囲取得するのと一緒。
# 値の更新区間への処理
while l < r:
if l & 1: # 奇数(=右側のセグメント)ならLazyを更新、右の部屋に行って(+1)から上層へ(>>1)。
self.lazy[l] = x
self.value[l] = x
l += 1
if r & 1:
r -= 1
self.lazy[r] = x
self.value[r] = x
l >>= 1
r >>= 1
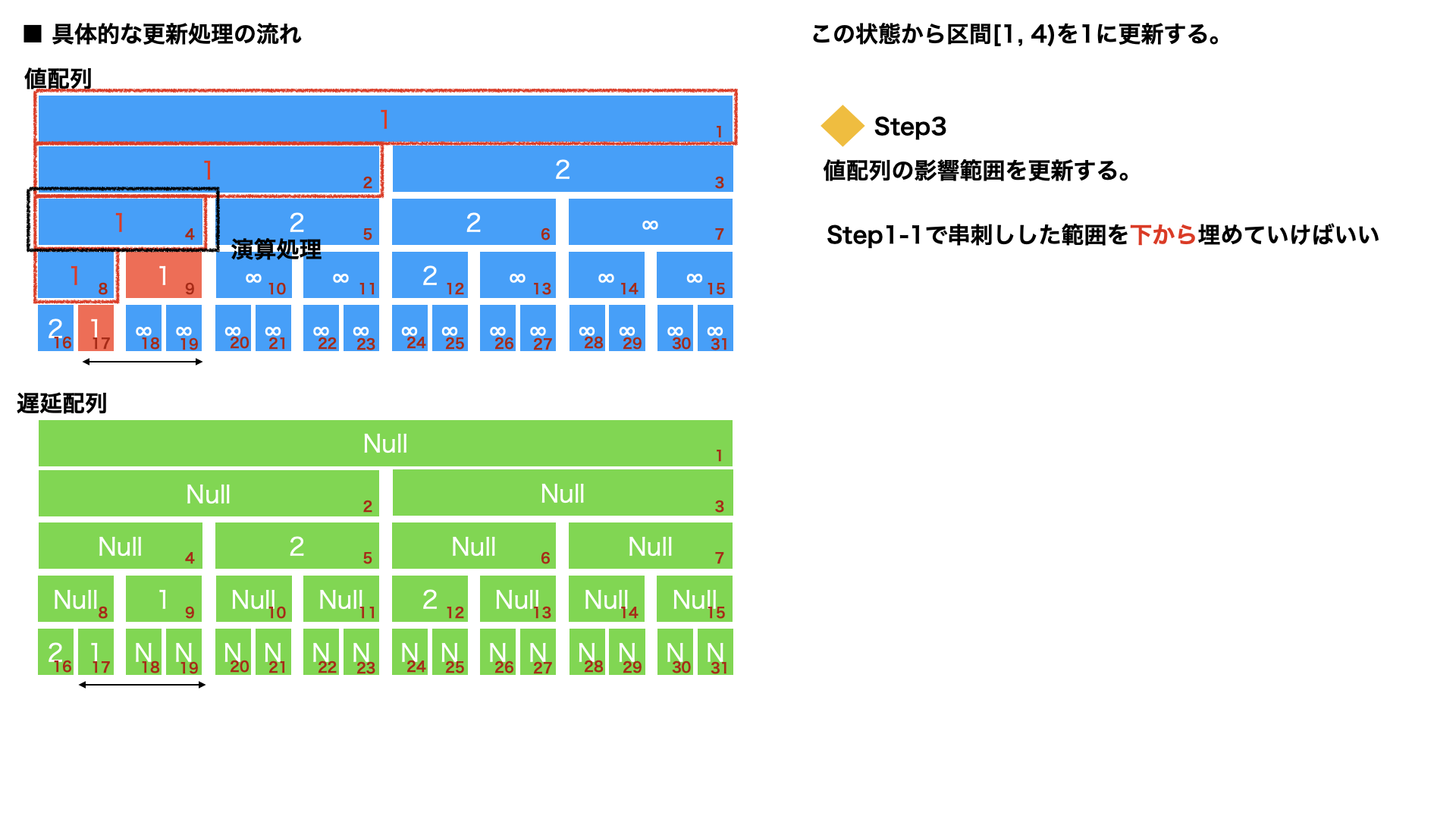
区間更新 : Step3
Step1-1でのジェネレータを利用。
for idx in self._gindex(l, r):
self.value[idx] = self.func(self.value[idx << 1], self.value[idx << 1 | 1])
区間取得 : Step1
区間更新のStep1と同じ。割愛。
区間取得 : Step2
vL = self.unit
vR = self.unit
while l < r:
if l & 1:
vL = self.func(vL, self.value[l])
l += 1
if r & 1:
r -= 1
vR = self.func(self.value[r], vR)
l >>= 1
r >>= 1
return self.func(vL, vR)
完成形
繋ぎ合わせたらOK。
以下でverify実施。
任意の演算への拡張
以下で挙げた中で更新処理をする部分には3通りあることに着目する。
変更処理A
遅延配列上の伝播処理。ここは更新を先送りしている値が並ぶので、更新クエリの処理に依存する。
更新クエリが上書きの問題では子の値は親の値で上書きするように処理を書き、加算の問題では子の値に親の値を加算するように処理を書く。
変更処理B
遅延配列→値配列へ適応する。ここは過去に評価を遅延した更新処理だけでなく更新クエリを受けた時に実施する更新処理でも呼ばれる。これは設問の更新クエリと取得クエリの両方に依存する。
更新は上書き、取得は最小値という問題(DSL_2_F)では更新時には単に上書きでいいが、更新は上書き、取得は合計値という問題(DSL_2_I)では更新時には下層のセグメント長分の合計値で更新する必要がある。
演算処理
値配列を上方向に伝播させる処理。これは取得クエリに依存する。
取得クエリが最小値なら最小値で、合計値なら合計値で更新する。
該当箇所の関数を切り出して上記3箇所を変更できるようにしたら良さそう。