いつ使うのか
N個の要素に対して繰り返し大小判定をし、
- 条件を満たす最大/最小の値を求めるとき。
- 条件を満たす要素を数え上げるとき。
- ソートしたリストのK番目を求めるとき。(リストのK番目の数字以下の数字の個数<=Kを満たす最大の値)
何がいいのか
通常、一個一個見ていくとO(N)のオーダーがかかるところをO(logN)に短縮することができる。
どうするのか
- 予めN個の要素をソートしておく。
- ソートした全要素の両端より
外側の値を2つ選ぶ。(=初期値を両端としてしまうとその点は評価されないため全てTrue/Falseだった場合に不正になる) - 次の操作を繰り返し、最終的には条件を満たすokと満たさないngの境界を求める。
- 2値の平均値(中点)が条件を満たすか判定し、満たすならokをその中点の値とする。満たさないならngを中点とする。
- okとngの絶対値の差が1未満になったら繰り返しを終了する。(=境界が求まった)
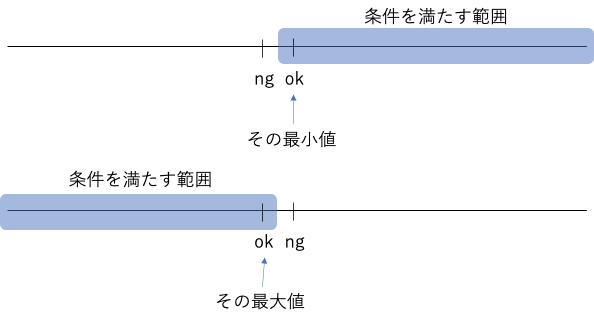
イメージ
考えること
ソートしたリストを条件によって篩にかけた時にどちら側がTrue/Falseになるか。
テンプレート
条件判定
def is_ok(mid: int):
# 検索対象の外にあるものは先に弾く(リストのインデックスなんかだとout of rangeするので)
if mid < 0:
return True | False # ※1
elif mid >= N:
return True | False
return True | False #判定条件の結果
※1 : 最終的なリストの状態の左側を指定。
-
True ----||---- False→True -
False ----||---- True→False
探索実行部分
def binSearch(ok: int, ng: int):
#print(ok, ng) # はじめの2値の状態
while abs(ok - ng) > 1: # 終了条件(差が1となり境界を見つけた時)
mid = (ok + ng) // 2
if is_ok(mid):
ok = mid # midが条件を満たすならmidまではokなのでokの方を真ん中まで持っていく
else:
ng = mid # midが条件を満たさないならmidまではngなのでngの方を真ん中まで持っていく
#print(ok, ng) # 半分に切り分ける毎の2値の状態
return ok # 取り出すのは基本的にokの方。(問題によりけり)
実行
# 探索範囲が0 ~ Nまでの場合。
INF = N + 1
binSearch(-1, INF)
- 実行する時は、両端より±1した場所から始める(なお、ここはどれだけ外の値を入れても問題ない)
- 呼び出す時はokとngに対応した引数の順で入れること。(あたりまえ)
使用例
1 条件を満たす最大の値を求めるシンプルなパターン
INF = 10 ** 9 + 1
def main():
A, B, X = map(int, input().split())
# True - ng - ok - False
def is_ok(mid: int):
# 判定する条件
if mid < 0:
return True
elif mid >= INF:
return False
return A * mid + B * len(str(mid)) <= X
def binSearch(ok: int, ng: int):
#print(ok, ng)
while abs(ok - ng) > 1:
mid = (ok + ng) // 2
if is_ok(mid):
ok = mid
else:
ng = mid
#print(ok, ng)
return ok
print(binSearch(0, INF))
return
2 条件を満たすものを数え上げるパターン
2-1 シンプルな問題
def main():
N = int(input())
L = [int(i) for i in input().split()]
L.sort()
# True ---- False
def is_ok_top(mid: int, a: int, b: int):
if mid < 0:
return True
elif mid >= N:
return False
return L[mid] < L[a] + L[b]
def binSearch_top(ok: int, ng: int, a: int, b: int):
while abs(ok - ng) > 1:
mid = (ok + ng) // 2
if is_ok_top(mid, a, b):
ok = mid
else:
ng = mid
return ok
count = 0
for a in range(0, len(L) - 2):
for b in range(a + 1, len(L) - 1):
count += binSearch_top(-1, INF, a, b) - b
print(count)
(PyPyでないとTLEした。)
2-2 閾値以上/以下の両方をそれぞれ二分探索
※ ポイント:3つの変動値がある時には中央を固定することでパターン数を抑えられる。
def solve(N: int, A: "List[int]", B: "List[int]", C: "List[int]"):
# 最大値 + 1を設定
INF = N + 1
A.sort()
B.sort()
C.sort()
# True - ok - ng - False
def is_ok(mid: int, b: int):
# 判定する条件
if mid < 0:
return True
elif mid >= N:
return False
return A[mid] < b
# False - ng - ok - True
def is_ok2(mid: int, b: int):
# 判定する条件
if mid < 0:
return False
elif mid >= N:
return True
return C[mid] > b
def binSearch(ok: int, ng: int, b: int):
#print(ok, ng)
while abs(ok - ng) > 1:
mid = (ok + ng) // 2
if is_ok(mid, b):
ok = mid
else:
ng = mid
#print(ok, ng)
return ok
def binSearch2(ok: int, ng: int, b: int):
#print(ok, ng)
while abs(ok - ng) > 1:
mid = (ok + ng) // 2
if is_ok2(mid, b):
ok = mid
else:
ng = mid
#print(ok, ng)
return ok
sum = 0
for b in B:
a = binSearch(-1, INF, b) - 0 + 1
c = N - 1 - binSearch2(INF, -1, b) + 1
sum += a * c
#print(b, "->", a, c)
print(sum)
return
3 ソートしたリストのK番目を求めるとき。(K番目の数字X以下の個数がK個以上を満たす最小のX)
より厳密には「一列に並べた時にK番目を求める問題。ただし膨大すぎて全ての要素を列挙できないとき。」
この問題はN^2個の数をソートしてK番目を求めればいいが最大 9 * 10^8 個はTLEする。
そこで問題の捉え方を変える。
K番目の数字Xを求める。= その数字X以下の個数がK個ある。
積X以下の個数がK個以上かどうかを条件として二分探索。
1,1,2,2,2,2,2,4,4 の5番目(K = 5)を求める時。
X = 1では2個 ( < 5 ) →ダメ
X = 2では7個 ( >= 5 ) →ok
5番目は2とわかる。
INF = 10 ** 18 + 1
def main():
N, K = map(int, input().split())
A = sorted([int(i) for i in input().split()])
B = sorted([int(i) for i in input().split()])
# False - ng - ok - True
def is_ok(mid: int):
# 判定する条件
if mid < 0:
return False
elif mid >= INF:
return True
count = 0
for a in A:
maxb = mid // a # 各aに対して積を取った時に値mid以下となる最大のbの値
count += bisect_right(B, maxb) # ソート済みのBからそのインデックスを求めれば、そこより手前のbは全てaとの積がn以下のbとなり個数がでる。
return count >= K
def binSearch(ok: int, ng: int):
#print(ok, ng)
while abs(ok - ng) > 1:
mid = (ok + ng) // 2
if is_ok(mid):
ok = mid
else:
ng = mid
#print(ok, ng)
return ok
print(binSearch(INF, 0))
return
参考