AtCoder D問題特訓 ABC166-157

入力の受け取りにはatcoder-tools使用。
https://github.com/kyuridenamida/atcoder-tools

ABC166 D - I hate Factorization

Xは10^9までという制約からA、Bの2数がたかだか-120〜120を検証してあげれば良いとわかる。 この計算量であれば十分全てを見れる。

def solve(X: int):
    for i in range(-120, 120):
        for j in range(-120, 120):
            if i ** 5 - j ** 5 == X:
                print(i, j)
                return

ABC165 D - Floor Function

引く数のfloor(x/B)が1を超えると途端に大きな数が惹かれるので、ここが0である中で最大になるものを選ぶ必要がある。→xはB-1がいいが、Nまでという制限で引っかかるならNを選択する。

def solve(A: int, B: int, N: int):
    x = min(B - 1, N)
    print(A * x // B)
    return

ABC164 D - Multiple of 2019

累積和の問題。

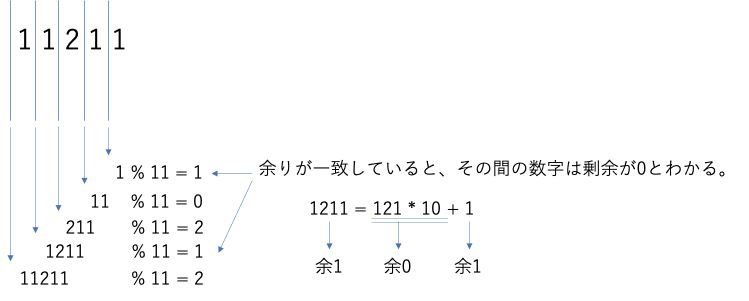
右からi番目までを取った時のi桁の数字を指定の数字で割った余りをリストにしていき、同じ余りとなる箇所同士の間の数字は割り切れると言える。

eg.) 11211から11で割りきれる部分の選び方。

def solve(S: str):

    l = [0] * 2019  # indexに対応する余りの数を保持するリスト
    ps = 0          # Sの部分列
    d = 1

    # 各桁までを2019で割った余りを算出し、カウント。
    for i in range(1, len(S) + 1):
        ps += int(S[-i]) * d % 2019
        l[ ps % 2019 ] += 1
        d = d * 10 % 2019

    # 余りが同じになる箇所2つの組み合わせを算出
    ans = 0
    for i in l:
        ans += i * (i - 1) // 2
    
    # あまり0となるところはそれ単体で割り切れる数列なのでカウント
    ans += l[0]
    print(ans)
    return

加減算、乗算は計算途中で剰余を出しても問題ない。それどころか今回のようなケースでは途中で余りに変えていかないとTLEする。→20万桁では処理が遅い。

ABC163 D - Sum of Large Numbers

Nが2×10^5なので、Nオーダーのループ1回程度が限度。

def solve(N: int, K: int):
    sum = 0
    for k in range(K, N + 2):
        sum += k * (N - k + 1) + 1
    
    print(sum % 1000000007)
    return

ABC162 D - RGB Triplets

Nは10^3なのでO(N^2)くらい、2重ループまでなら行けそうと見積もれる。

条件1にマッチする選び方は文字列SからR,G,Bを1つ選ぶ方法に一致し、これは簡単かつ高速に求まる。
なので、条件2にマッチしないものをそこから引いて答えとすることを考える。

from collections import defaultdict

def solve(N: int, S: str):
    sub = 0
    rgb = defaultdict(int)

    for i in range(N):
        # RGBそれぞれの個数をカウント
        rgb[S[i]] += 1
        # 条件2に一致しないケースをカウント
        for j in range(i + 1, N):
            if 2 * j - i >= N:
                break
            if S[i] != S[j] and S[j] != S[2 * j - i] and S[i] != S[2 * j - i]:
                sub += 1

    print(rgb["R"] * rgb["G"] * rgb["B"] - sub)
    return

ABC161 D - Lunlun Number

キューを使った問題。元々にルンルン数だった数字の末尾に適切な数字を付け足してルンルン数を増やしていく関係にあるところから幅優先探索のような感じを思いつく。

キューにルンルン数を詰めておき、1つずつ取り出してくる。
取り出したら、以下のルールにしたがって次のルンルン数をキューに詰めていく。

N = 1 ~ 8 → NとN±1を末尾に追加
N = 0 → NとN+1を末尾に追加
N = 9 → N-1とNを末尾に追加

import queue

def solve(K: int):
    q = queue.Queue()
    # initialize
    for i in range(1, 10):
        q.put(i)
    
    # 取り出してきて次のルンルン数をキューに追加。
    for i in range(K):
        res = q.get()
        first = res % 10
        if first == 0:
            q.put(res * 10 + first)
            q.put(res * 10 + first + 1)
        elif first == 9:
            q.put(res * 10 + first - 1)
            q.put(res * 10 + first)
        else:
            q.put(res * 10 + first - 1)
            q.put(res * 10 + first)
            q.put(res * 10 + first + 1)

    print(res)
    return

ABC160 D - Line++

10^3程度なので2重ループしても良さそうと見積もる。
横道XYを使った時と使わない時のそれぞれの距離のうち短い方をとって各(i, j)のケースの距離を算出する。
i < jが約束されているので、横道を使う時はi~Xの距離＋X~Yの距離(1)＋j~Yの距離の和とみなせる(場合分けは不要)。

def solve(N: int, X: int, Y: int):
    distances = [0] * (N - 1)
    for i in range(0, N - 1):
        for j in range(i + 1, N):
            distance = min(j - i, abs(X - 1 - i) + abs(Y - 1 - j) + 1)
            distances[distance - 1] += 1

    for k in distances:
        print(k)
    return

ABC159 D - Banned K

Nは2×10^5なのでk = 1,2,…,Nの1週しかループできない。
全体を求めるのはループがいらないので、引き算の手法で解く。

def solve(N: int, A: "List[int]"):
    nums = [0] * N
    # どの数字がいくつあるかカウント
    # 最終的にリストのi - 1番目に数字iの個数が入る。
    for i in A:
        nums[i - 1] += 1
    
    # 組み合わせの総和を算出
    sum = 0
    for num in nums:
        sum += num * ( num - 1 ) // 2

    # k番目のボールを抜くことでk番目に書かれていた数字A[k]の個数が1つ減る。
    # それによって減少する組み合わせの個数を算出し、総和から差し引く。
    for k in range(0, N):
        old = nums[A[k] - 1]
        new = old - 1
        ans = sum - (old * (old - 1) // 2 - new * (new - 1) // 2)
        print(ans)
    

    return

ABC158 D - String Formation

dequeを使えるかの問？

・反転処理の扱い
最終的に偶数回受ける　→ 反転しないのと等価。
最終的に奇数回受ける　→ 1回反転するのと等価。

とはいえ、途中の反転状態によって追加する文字を先頭に追加するか、末尾に追加するかが変わるのでステータスを持っておく必要はある。

from collections import deque

def solve():
    S = input()
    ans = deque()
    ans.append(S)
    Q = input()
    reverseFlg = False
    for _ in range(int(Q)):
        TFC = input()
        l = TFC.split()
        if l[0] == "1":
            reverseFlg = not reverseFlg
        else:
            # 反転フラグが立っているなら、本来先頭に追加するの(F = 1)は末尾に追加
            # そうでないなら指示通り先頭に追加。 逆もまた然り。
            if reverseFlg:
                if l[1] == "1":
                    ans.append(l[2])
                else:
                    ans.appendleft(l[2])
            else:
                if l[1] == "1":
                    ans.appendleft(l[2])
                else:
                    ans.append(l[2])
    
    # 最終的にフラグが立っているかどうかで反転処理の有無を判断
    res = ''.join(ans)
    if(reverseFlg):
        print(res[::-1])
    else:
        print(res)

    return 

条件分岐がごちゃごちゃするのでXNORとか書けたらスマートかも。

ABC157 D - Friend Suggestions

UnionFind木の問題。
繋がっている人の数 - その中でブロックしてる人の数 - すでに友人関係の数 - 1(自分)で算出できる。
この人の回答が勉強になった。 https://atcoder.jp/contests/abc157/submissions/12572173