前書き
最近Web系企業のインターン選考や本選考を受ける機会が何度かありました。
多くの企業の選考でコーディングテストがありまして、今回少し勉強したのでアウトプットの練習も兼ねて備忘録的な感じで残しておきます。
今回はメモ化についてです。
メモ化とは
簡単に言うと、プログラムの高速化のためのテクニックです。
「再帰処理などで何度も同じ関数が呼ばれる際に計算結果をキャッシュ(メモ)に記録しておき、前に計算したものに関してはキャッシュされた値を返す」といった感じのテクニックです。
実装例
今回は実装例として、フィボナッチ数列のn番目の数字は何かを求めるプログラムを紹介します。
フィボナッチ数列
a_1=a_2=1 \\
a_n=a_{n−1}+a_{n−2}\\
(1\leqq n)
フィボナッチ数列を漸化式で表すと上記のようになります。
詳しい説明は省略しますが、最初の2つの項は1を返し、それ以降は前の2つの項の和を返します。
ただの再帰で実装
def fibonacci(n):
if n == 1 or n == 2:
return 1
return fibonacci(n - 2) + fibonacci(n - 1)
print(fibonacci(6)) # 8
メモ化で実装
memo = {1: 1, 2: 1}
def fibonacci(n):
# memoの中にnが記録されている場合は、その値を返す
if n in memo:
return memo[n]
# ない場合はメモに記録して、その値を返す
memo[n] = fibonacci(n - 2) + fibonacci(n - 1)
return memo[n]
print(fibonacci(6)) # 8
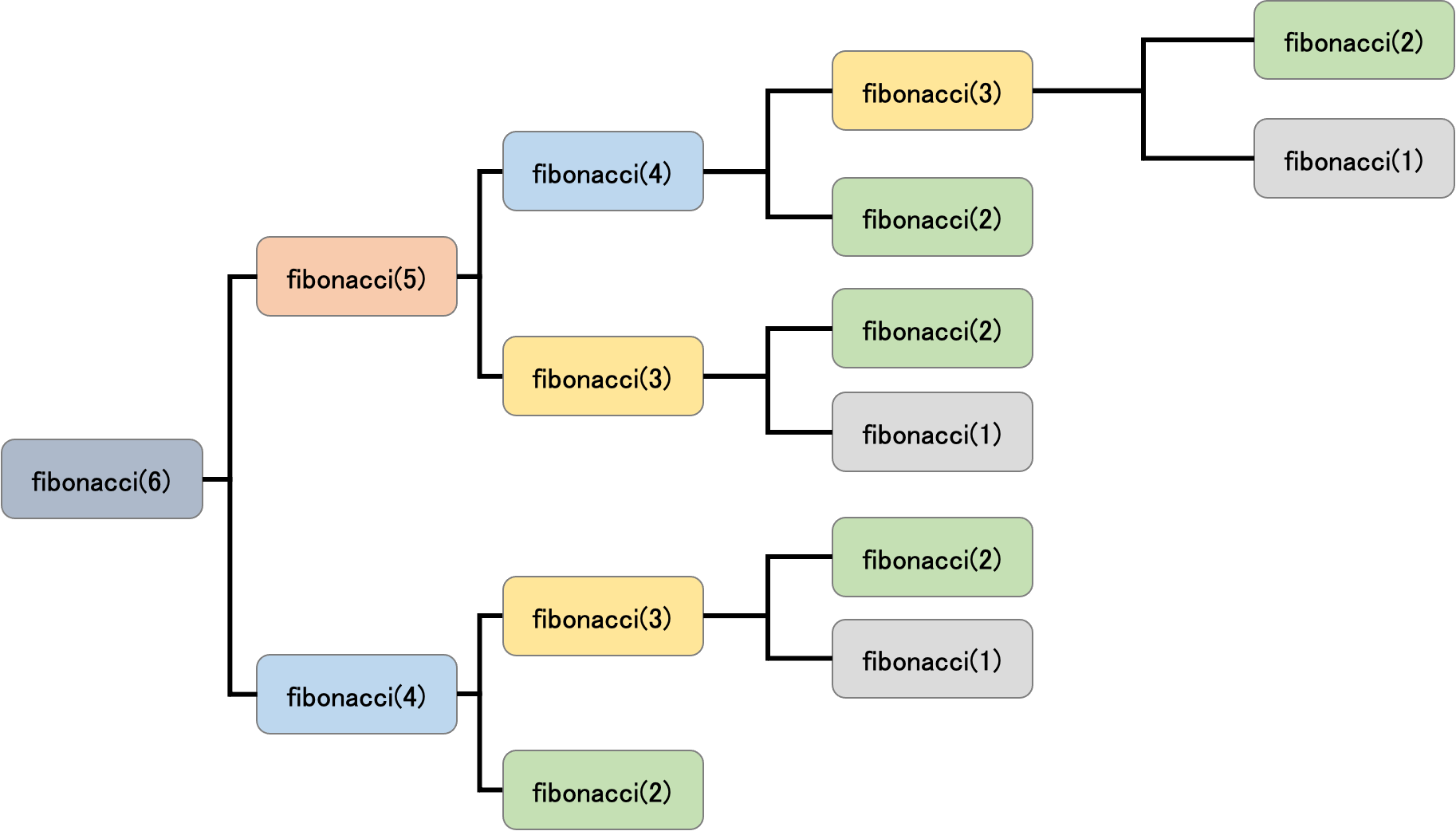
イメージ
ただの再帰で実装した場合のn=6は、fibonacci(4)が2回、fibonacci(3)が3回呼ばれています。
nがどんどん大きくなると、計算する回数が増えていくことがイメージできると思います。
メモ化をすると1度計算したものについて2回目以降は計算しなくて済むので、計算回数を大幅に減らすことができます。
まとめ
- メモ化はプログラムの高速化のためのテクニックの1つ。
- nが大きくなればなるほど有効