Python：機械学習とモデル取得の手順

この記事では、機械を訓練してモデルを取得するための主な手順、簡単な練習方法を紹介し、機械学習の基本原理を共有します。

著者： Xixia

1）機械学習とは何か、なぜ必要なのか？

機械学習とは何か、まず2つの例を見てみましょう。

動物を「猫」と認識する学習法とは？

小さな赤ちゃんのように、猫を見たことがない人を想像してみてください。彼らには、「猫」という言葉すらありません。

ある日、彼らはこのような毛むくじゃらの動物を目にします。

彼らはそれが何であるかを知らないので、あなたはそれが「猫」であることを彼らに伝えます。

しばらくすると、また同じような動物が出てきます。

あなたは彼らに、それも猫であると言います。

その後、彼らはまた別の動物を見ます。

このとき、彼らは「猫」を見たとあなたに直接伝えます。

先の方法は、私たちが世界を理解するための基本的な方法であるパターン認識です。私たちは、豊富な経験に基づいて、それが猫であると結論づけました。

この過程で、私たちは様々な猫であるサンプルに接触することで、猫の特徴を学びました。読書で学び、鳴き方や、2つの耳、4本の足、尻尾、ヒゲなどの姿を観察して、結論を出します。そして、猫とは何かを知るのです。

どのようにしてテスト用のnpmパッケージを識別するのか？

以下は、私の同僚が書いたコードの一部です。

SELECT * FROM
  tianma.module_xx
WHERE
  pt = TO_CHAR(DATEADD(GETDATE(), - 1, 'dd'), 'yyyymmdd')
  AND name NOT LIKE '%test%'
  AND name NOT LIKE '%demo%'
  AND name NOT LIKE '%测试%'
  AND keywords NOT LIKE '%test%'
  AND keywords NOT LIKE '%测试%'
  AND keywords NOT LIKE '%demo%'

もちろん、モジュールの名前やキーワードに「test」や「demo」といった文字が含まれているかどうかが基準となります。これが当てはまれば、テストモジュールと判断します。私たちのルールをデータベースに伝えることで、データベースはテストモジュールではないものを選別してくれるのです。

猫の識別は、テストモジュールの識別と基本的には同じです。どちらも特徴を探すことになります。

• 猫の特徴：鳴き声、両耳、4本足、尻尾、ヒゲ
• テストモジュールの特徴：テストまたはデモ

この特徴は、さらに次のようにプログラムすることができます。

• 猫の特徴：鳴き声：真、耳：2、足：4、尻尾：1、ヒゲ：10
• テストモジュールの特徴：test:count>0またはdemo:count>0

これらの特徴があれば、人も機械も猫やテストモジュールを認識することができます。

簡単に言うと、機械学習では特性とその重みを使ってデータの分類を行います。このような簡略化された記述は、理解を容易にするためのものです。詳しくは、GitHubのmaster apachecn/AiLearningにあるAiLearning/1. Basic Machine Learning.mdをご覧ください。

なぜ機械学習が必要なのか？

その理由は、分類タスクに大量の特性が含まれる場合、「if-else」を使って単純な分類を行うことが難しいからです。一般的な商品推奨アルゴリズムを例に挙げてみましょう。ある製品を誰かに勧めるべきかどうかを識別するために、アルゴリズムには何百もの特性が含まれることがあります。

2) どのようにして機械を訓練し、モデルを取得することができるか？

データの準備

データの準備は、機械学習のタスク全体で消費される時間の75％以上を占めると言われています。そのため、最も重要で最も難しい部分です。主な手順は以下の通りです。

1) 基本データを収集する。
2) 外れ値を取り除く。
3) 可能な特性を選択する：characteristic engineering
4) データにタグを付ける。

アルゴリズムの準備

データを関数に当てはめます：y = f(x)

例えば、一次関数を使用します： y = ax + b

アルゴリズムを評価する

適切な「a」と「b」の値が得られたかどうかを調べるには、評価関数を使います。

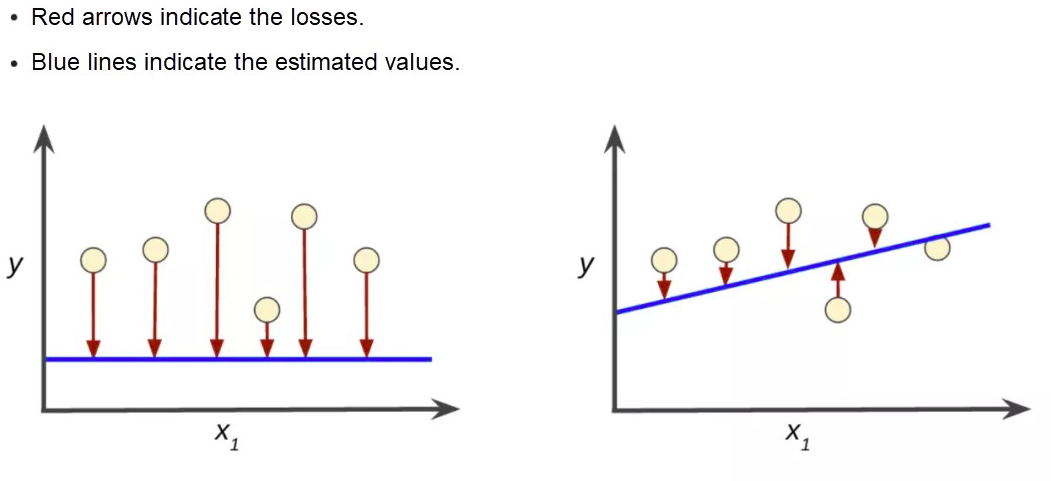
評価関数は、学習によって得られたパラメータと実際の値との差を記述します。この差を損失値とも呼びます。次の図は、その例です。

右側の青い線の方が実際のデータポイントに近いです。

損失評価関数として最も一般的なものは，平均自乗誤差である．この関数は、推定値と実際の値の平均的な二乗差を測定し、推定値の品質を判断します。

前述の図に示すように，サンプル中の小さな黄色の円の座標は以下の通りです。

[
[x1, y1],
[x2, y2],
[x3, y3],
[x4, y4],
[x5, y5],
[x6, y6]
] 

青線上の推定座標は以下の通りです。

[
x1, y'1],
x2, y'2],
x3, y'3],
x4, y'4],
x5, y'5],
x6, y'6]
] 

したがって、損失額は

const cost = ((y'1-y1)^2 + (y'2-y2)^2 + (y'3-y3)^2 + (y'4-y4)^2 + (y'5-y5)^2 + (y'6-y6)^2 )/6

アルゴリズムの学習

放物線の最下点に基づいて適切なaおよびbの値を求める
先ほどの一次関数を例にとると、このようになります。アルゴリズムの学習とは、実際に「a」と「b」の適切な値を探すことです。膨大な数の海の中を無作為に検索しても、「a」と「b」の適切な値を見つけることはできません。この場合、「a」と「b」の適切な値を見つけるために、勾配降下法のアルゴリズムを使用する必要があります。

ゴールを明確にするために、先ほどの損失値の計算式をy = ax + bに置き換えます。

// Function 2
const cost = (((a*x1+b)-y1)^2 + ((a*x2+b)-y2)^2 + ((a*x3+b)-y3)^2 + ((a*x4+b)-y4)^2 + ((a*x5+b)-y5)^2 + ((a*x6+b)-y6)^2 )/ 6

私たちの目標は、コストを最小化する「a」と「b」の値を見つけることです。このゴールがあれば、そのまま解答を求めることができるかもしれません。

中学校で習った二次関数、つまりy = ax^2 + bx + cという二次方程式をまだ覚えていますか？

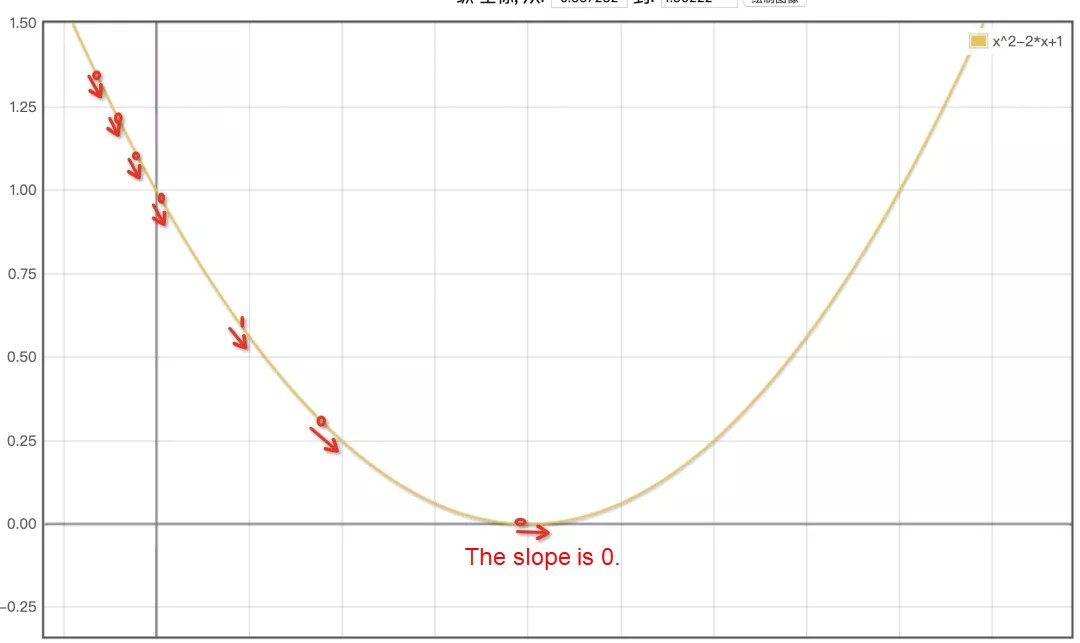
先のコスト関数は長いように見えますが、これも二次関数です。そのグラフはおそらく次のようなものです。

最下点の「a」と「b」の値を求めることができれば、目的を達成することができるのです。

放物線の最下点を、最下点でゼロになる傾きで特定する
a」の値をランダムに1に初期化したとすると、その点は放物線の左上にあり、コストが最小となる最下点からはまだ遠いです。

前述の図のように、最低点に近づくにはaの値を大きくすればよいですが、機械はそのグラフを理解することができません。この場合、今回の記事の中で最も複雑な数学的知識である「微分」に注目します。このとき、接線の傾きは、先のグラフの最下点（傾きが0）など、この放物線の微分値となります。

この微分によって、ここの接線（斜めの赤い線）の傾きを計算することができます。この斜線の傾きが負であれば、aの値が小さすぎて、底に近づけるためには大きくする必要があることを意味します。逆に、傾きが正であれば、aの値が最低点を通過したので、底辺に近づくためには減らす必要があることを意味します。

コスト関数の導関数を求めるには？
次のコードを見てみましょう。このコードを理解するためには、まず数学的な知識である偏微分と合成関数の微分の求め方を確認してください。

// Function 3
// Partial derivative of a
const costDaoA = (((a*x1+b)-y1)*2*x1 + ((a*x2+b)-y2)*2*x1 + ((a*x3+b)-y3)*2*x1 + ((a*x4+b)-y4)*2*x1 + ((a*x5+b)-y5)*2*x1 + ((a*x6+b)-y6)*2*x1 )/ 6

// Partial derivative of b
const costDaoB = (((a*x1+b)-y1)*2 + ((a*x2+b)-y2)*2 + ((a*x3+b)-y3)*2 + ((a*x4+b)-y4)*2 + ((a*x5+b)-y5)*2 + ((a*x6+b)-y6)*2 )/ 6

a' と 'b' の値を costDaoA 関数に持ち込むと、傾きが得られます。これは、底辺に近づくためにパラメータ 'a' をどのように調整するかを決定します。

同様に、costDaoBはパラメータ'b'をどのように調整すれば底辺に近づけるかを決定します。

500サイクルの走行
このようにして500サイクル走らせると、かなり底辺に近づき、適切な'a'と'b'の値を得ることができます。

モデルの入手

y = ax + b のようなモデルを得て、これを使って推定を行います。

3）簡単な練習から始める：線形回帰

線形回帰とは？

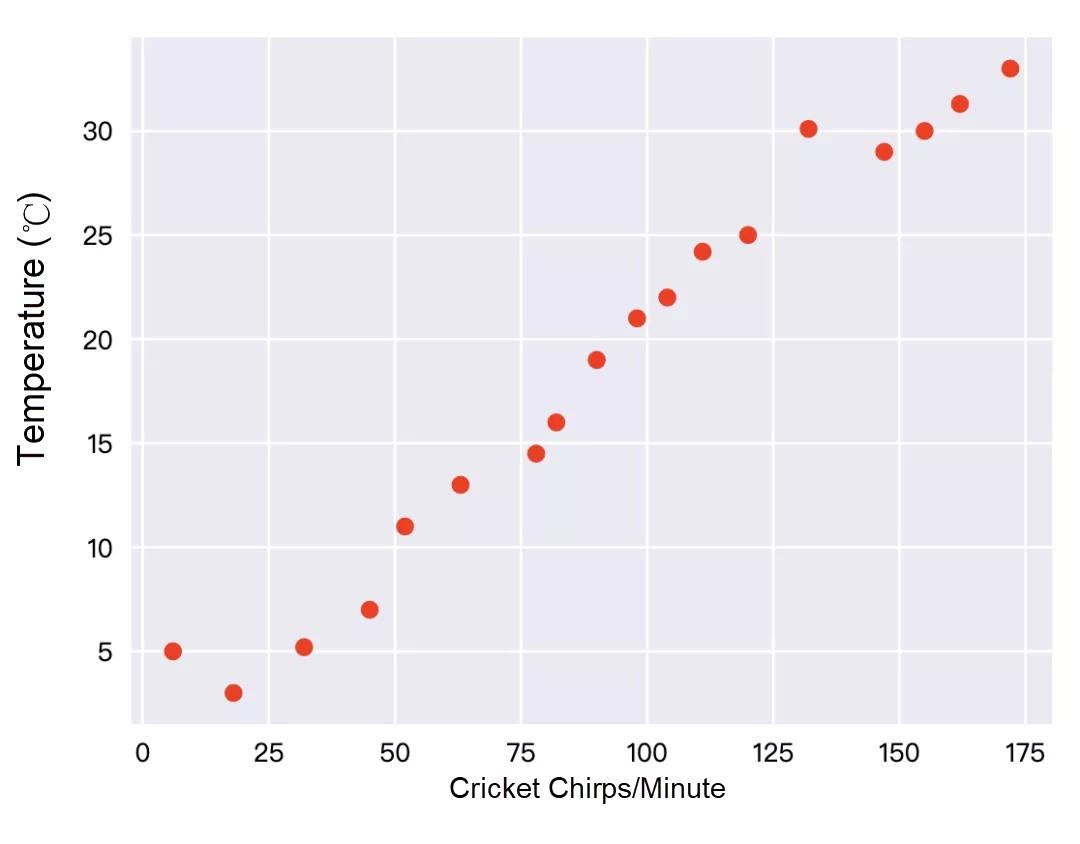
コオロギの鳴き声は、涼しいときよりも暑いときの方が多いことは誰もが知っています。気温と1分間のコオロギの鳴き声を表に記録し、エクセルで次のようにグラフ化してみました（事例はGoogle TFの公式チュートリアルから）。

この赤い点がほぼ一直線上にあることがわかります。

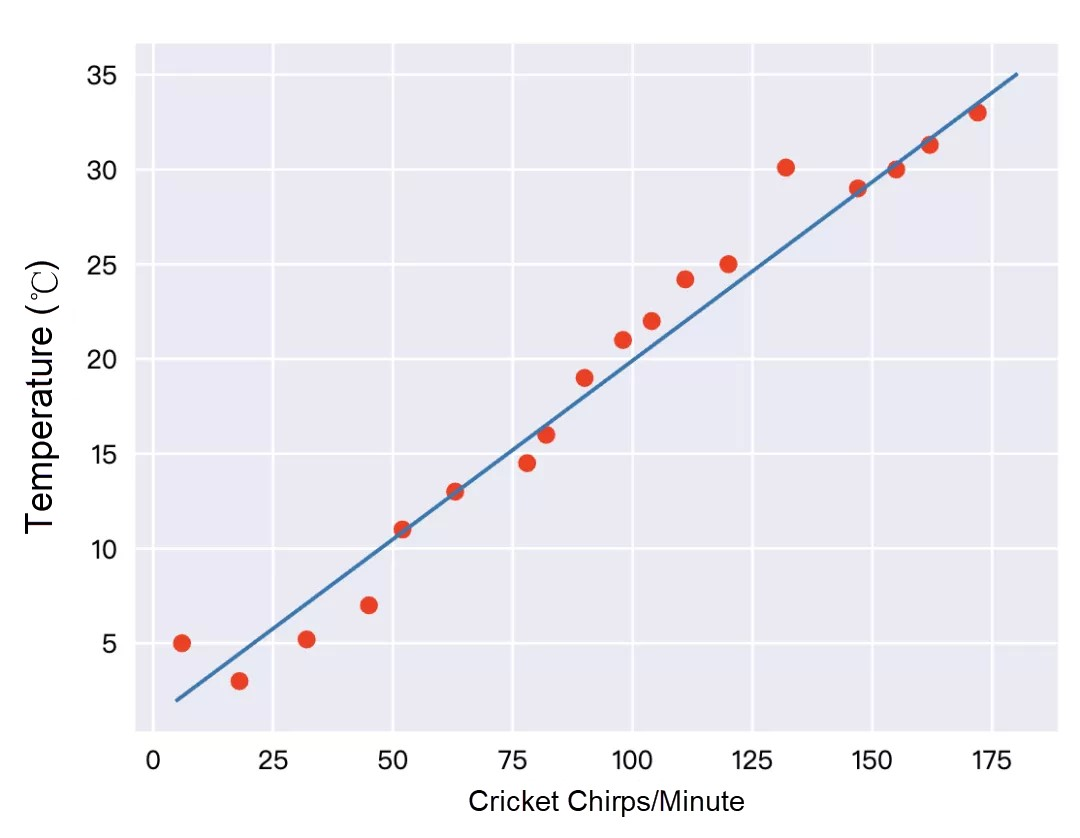
そこで、データの分布を直線とみなし、この直線を引く作業を線形回帰といいます。この直線があれば、どのような状況でも1分間のコオロギの鳴き声を正確に推定することができます。

ブラウザを使った線形回帰の実演

アドレス：テスト勾配降下法

https://jshare.com.cn/feeqi/CtGy0a/share?spm=ata.13261165.0.0.6d8c3ebfIOhvAq

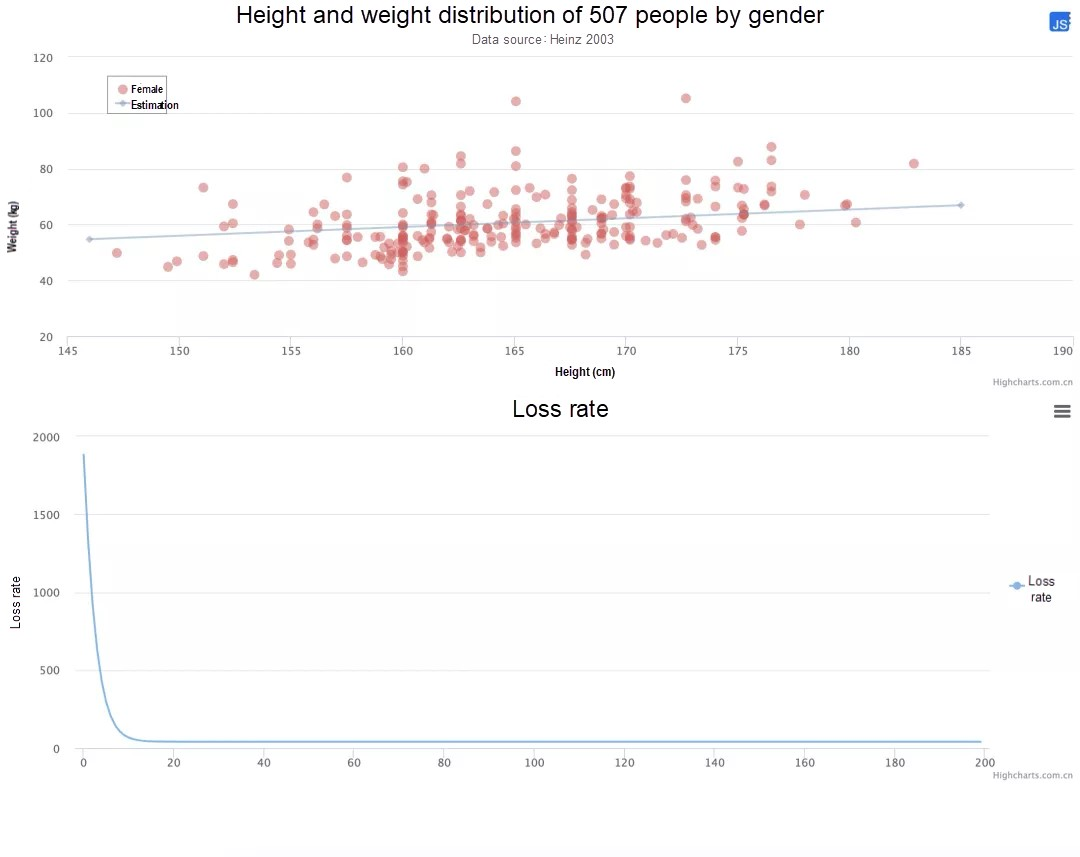
データの可視化にはhighchartsを使用し、highchartsのデフォルトのデータポイントを直接使用することで、消費される時間の75%を節約しています。

トレーニングが完了すると、グラフ上に青い線が重ねられ、各トレーニングサイクルの'a'と'b'の値の損失率曲線が追加されます。

コードの説明

/**

* Cost function and calculation of the mean squared error

*/

function cost(a, b) {

    let sum = data.reduce((pre, current) = >{

        return pre + ((a + current[0] * b) - current[1]) * ((a + current[0] * b) - current[1]);

    },
    0);

    return sum / 2 / data.length;

}

/**

* Calculate the gradient

* @param a

* @param b

*/

function gradientA(a, b) {

    let sum = data.reduce((pre, current) = >{

        return pre + ((a + current[0] * b) - current[1]) * (a + current[0] * b);

    },
    0);

    return sum / data.length;

}

function gradientB(a, b) {

    let sum = data.reduce((pre, current) = >{

        return pre + ((a + current[0] * b) - current[1]);

    },
    0);

    return sum / data.length;

}

// Number of training cycles
let batch = 200;

// This is the speed at which the result value gets closer to the bottom in each cycle. It is also the learning speed. If it is too high, the result value will bounce around the lowest point. If the speed is too low, the learning efficiency will become lower.
let alpha = 0.001;

let args = [0, 0]; // Initialized a and b values
function step() {

    let costNumber = (cost(args[0], args[1]));

    console.log('cost', costNumber);

    chartLoss.series[0].addPoint(costNumber, true, false, false);

    args[0] -= alpha * gradientA(args[0], args[1]);

    args[1] -= alpha * gradientB(args[0], args[1]);

    if ((—batch > 0)) {

        window.requestAnimationFrame(() = >{
            step()
        });

    } else {

        drawLine(args[0], args[1]);

    }

}

step();

4）次のステップ

学習モデルを得るためには、より多くの特性がある場合には、より多くの計算を行い、より多くの時間をかけて学習を行う必要があります。

ここまでの簡単な説明を読んでいただければ、機械学習はもう間違いなく理解できるようになります。そしてより専門性の高い入門記事を参考にしてください。

Alibaba CloudでAI/MLを始めることに興味がある方は、Machine Learning Platform for AI（PAI）のページをご覧ください。

参考文献

1) GitHub - apachecn/AiLearning: AiLearning: 機械学習 - MachineLearning - ML, 深層学習 - DeepLearning - DL, 自然言語処理 - NLP
2) https://developers.google.com/machine-learning/crash-course/descending-into-ml/video-lecture?hl=zh-cn
3) ゼロから学ぶ機械学習：Pythonによる勾配降下法の実装方法をステップバイステップで解説

ここに記載されている見解は参考情報であり、必ずしもAlibaba Cloudの公式見解を示すものではありません。

本ブログは英語版からの翻訳です。オリジナルはこちらからご確認いただけます。一部機械翻訳を使用しております。翻訳の間違いがありましたら、ご指摘いただけると幸いです。

アリババクラウドは日本に２つのデータセンターを有し、世界で60を超えるアベラビリティーゾーンを有するアジア太平洋地域No.1(2019ガートナー)のクラウドインフラ事業者です。
アリババクラウドの詳細は、こちらからご覧ください。
アリババクラウドジャパン公式ページ