本記事では、北京、成都、杭州で開催されたPyCon China 2018カンファレンスで発表されたMarsの「What, Why, and How」を共有しています。
本ブログは英語版からの翻訳です。オリジナルはこちらからご確認いただけます。一部機械翻訳を使用しております。翻訳の間違いがありましたら、ご指摘いただけると幸いです。
背景
まず、これはscipyの技術スタックのパノラマです。NumPyが基盤となっています。多次元配列のデータ構造と、その上で動作する様々な計算を提供します。その上で、主に様々な科学計算を行うscipy、DataFrameを中心としたpandasに注目してください。表型データの処理やクリーニングなどの機能を提供しています。次のレベルでは、機械学習フレームワークとしてよく知られている古典的なライブラリであるscikit-learnがあります。トップレベルには、主に天文分野を指向した astropy や、生物分野を指向した biopython など、縦割りの分野向けのライブラリがずらりと並んでいます。
scipyの技術スタックを見ると、numpyが重要な役割を果たしていることがわかりますが、上位レベルのライブラリの多くはnumpyが提供するデータ構造や計算を利用しています。
実世界のデータは、表などの二次元データのように単純なものではありません。ほとんどの場合、多次元のデータを扱わなければならないことが多く、例えば、一般的な画像処理では、処理対象のデータは、画像の枚数、画像の長さや幅、RGBAチャンネルなどで、これが4次元データを構成しています。このような例は数え切れないほどあります。このような多次元処理能力があれば、より複雑な、あるいは科学的な分野の様々な処理にも対応できるようになり、また、多次元データ自体が2次元データを含んでいるので、表型データの処理も可能です。
また、データの内部を探る必要がある場合には、表型データに対して統計などの演算を行うだけでは絶対に足りません。行列の乗算やフーリエ変換など、より深いレベルでデータを分析するためには、より深い「数学的」な手法を使う必要があります。numpyは数値計算のためのライブラリなので、様々な上位レベルのライブラリと合わせて、これらのニーズを満たすのに非常に適していると考えています。
なぜMarsなのか?
では、なぜMarsプロジェクトに取り組む必要があるのでしょうか?例を挙げてみましょう。
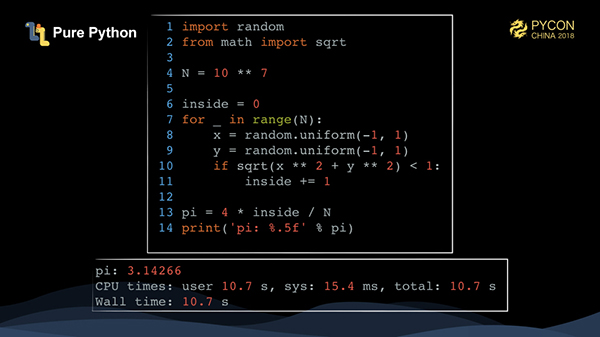
モンテカルロ法を使って円周率を計算してみます。この方法は、乱数を使って特定の問題を解くという、実はとてもシンプルなものです。図のように、半径1の円と辺の長さ2の正方形を用意し、たくさんの乱数点を生成して、右下の式、つまり、円の中に落ちている点の数を点の総数で割ったものに4をかけたものを使って、πの値を計算してみます。ランダムに生成された点の数が多いほど、計算された円周率の精度が高くなります。
これは純粋なPythonを使って非常に簡単に実装できます。N回トラバースしてX点とY点を生成し、それが円の中に入るかどうかを計算するだけです。1000万点を走らせるのに10秒以上かかります。
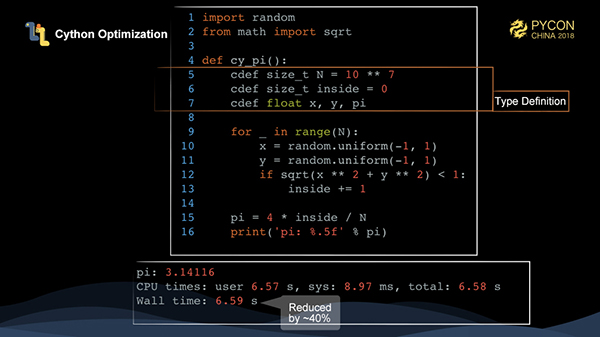
Pythonのコードの実行時間を短縮するための一般的な方法として、Cythonがあります。CythonはPython言語のスーパーセットを定義し、それをc/c++に翻訳し、コンパイルすることで実行を高速化します。ここでは、数種類の変数を追加していますが、純粋なPythonと比較して40%の性能向上が見られます。
Cythonは今やPythonプロジェクトの標準的な構成となっており、Pythonのコアサードパーティライブラリは基本的にCythonを使ってPythonのコード実行を高速化しています。
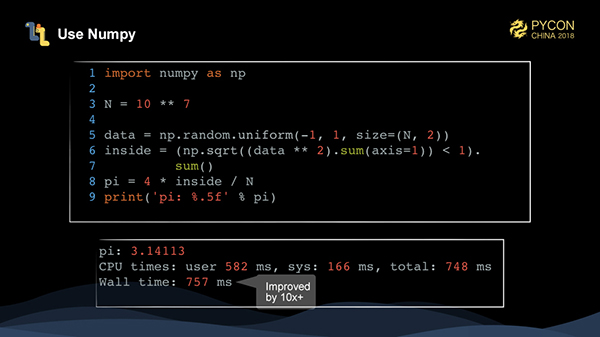
この例のデータは1つの型なので、専用の数値計算ライブラリを使ってベクトル化することで、このタスクの実行速度を非常に速くすることができます。Numpyは必然的な選択です。numpyで必要なのは、ループを減らす配列指向の考え方です。まず、numpy.random.uniformを使って2次元の配列をn個生成し、次にdata * 2を使って配列内の全てのデータを2乗し、次にsum(axis=1)を使って軸=1(つまり行方向)を合計します。
このとき、長さNのベクトルを取得し、numpy.sqrtを使ってベクトルの各値の2乗を求めます。結果 < 1 の場合は、各点が円の中に入るかどうかを判定するためのブール値のベクトルを取得します。最後に和をたどることで、点の総数を求めることができます。numpyを使い始めるのは最初は難しいかもしれませんが、慣れてくると、この書き方がいかに便利なものであるかを実感できるはずです。実際には非常に直感的です。
このように、numpyを使うことで、よりシンプルなコードが書けるようになり、純粋なPythonの10倍以上のパフォーマンスが大幅に向上しています。
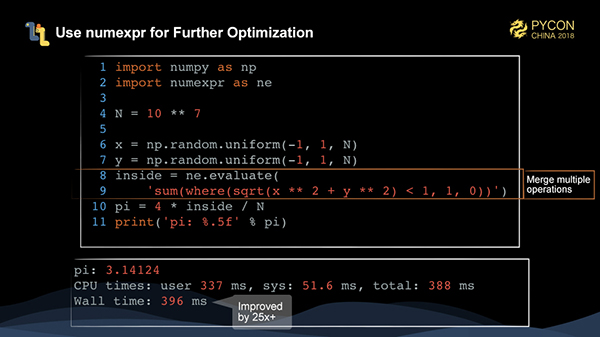
numpyコードは最適化できるのでしょうか?答えはイエスです。numexprというライブラリを使って、いくつかのnumpy演算を1つの演算に融合させ、numpyの実行を高速化しています。
ご覧のように、numexprによって最適化されたコードのパフォーマンスは、純粋なPythonコードの25倍以上になります。
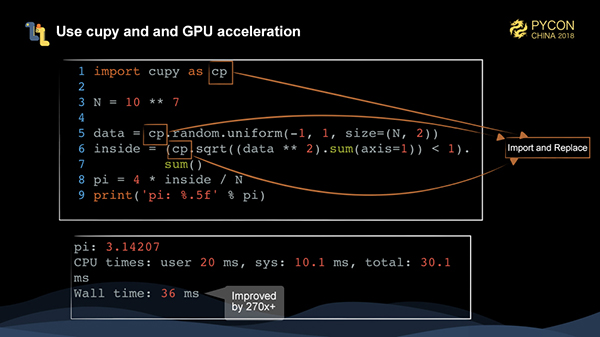
この時点ですでにコードはかなり高速に動いています。GPUがあれば、ハードウェアを使ってタスクの実行を高速化することができます。
この手のタスクには、numpyと整合性のあるAPIを提供するcupyというライブラリが強く推奨されています。importを置き換えるだけで、NVIDIAのグラフィックカード上でnumpyのコードを実行することができます。
この時点で、270倍以上の大幅な性能向上を実現しています。これはかなり注目に値する。
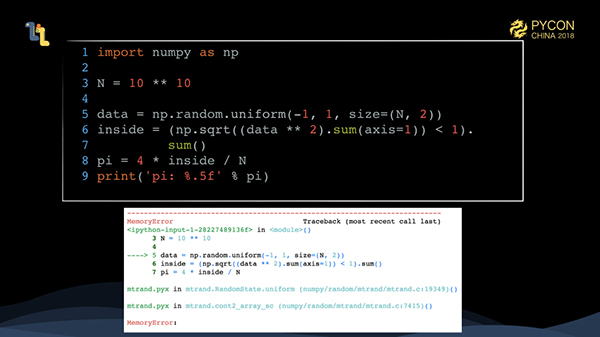
モンテカルロ法の精度を上げるために、計算量を1,000倍に増やしています。この状況ではどうなるのでしょうか?
はい、これは私たちが時々遭遇するメモリオーバーフロー(OutOfMemory)です。さらに悪いことに、jupyterでは、OutOfMemoryによってプロセスが強制終了されたり、以前の実行が失われたりすることがあります。
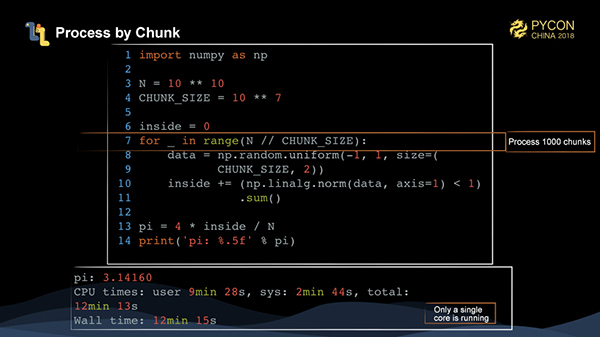
モンテカルロ法は比較的簡単に扱える。問題を1000ブロックに分けて、それぞれ1000万個のデータを解いて、ループを書いて合計を作るだけです。しかし、全体の計算時間は12分以上と遅い。
この時点では、全体の操作中に1つのCPUだけが実際に動作していて、他のコアは動作していないことがわかります。では、どうやってnumpy内の操作を並列化すればいいのでしょうか?
numpyの中には、行列の乗算にテンソルドットを使うなど、並列化できるものもありますが、それ以外のほとんどの操作は複数のコアを使うことができません。それ以外のほとんどの操作は、複数のコアを使うことができません。numpy内で演算を並列化するには、以下のような方法があります。
1、マルチスレッドやマルチプロセスを使ってタスクを書く
2、分散型メソッドを使用する
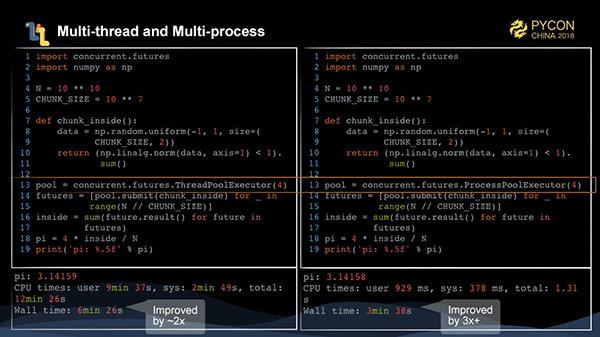
モンテカルロ法でπを計算するタスクをマルチスレッド、マルチプロセスの実装に書き換えるのはまだ簡単です。1000万件のデータエントリを処理する関数を書きます。そして、この関数を concurrent.futures の ThreadPoolExecutor と ProcessPoolExecutor を通してそれぞれ1000回投入し、マルチスレッドとマルチプロセスで実行させます。これにより、2〜3倍の性能向上が見られることがわかります。
しかし、モンテカルロ法による円周率の計算は非常に簡単に並列に書かれているので、もっと複雑な状況を考える必要があります。
import numpy as np
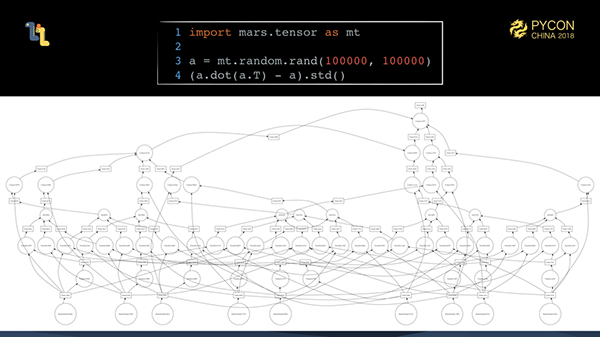
a = np.random.rand(100000, 100000)
(a.dot(a.T) - a).std()
100,000 * 100,000の行列「a」を作成しましたが、入力は約75GBです。行列 "a "に "a "の転置をかけ、"a "自体を引き算し、最後に標準偏差を計算します。このタスクの入力データは簡単にメモリに詰め込むことができず、その後の並列書き込み作業はさらに大変です。
ここで、どのようなフレームワークが必要なのかという疑問が出てきます。理想的には、私たちのフレームワークは以下の要件を満たすことができなければなりません。
- 馴染みのあるインターフェースを提供すること。例えば、Cupyは "import "を置き換えるだけで、元々numpyで書かれていたコードを並列化することができます。
- スケーラブルであること。スタンドアロンマシンのように小さくても、マルチコア並列処理が可能であること。大規模なクラスタほどの規模であれば、数千台のマシンを分散してまとめてタスクを扱うことができる。
- タスクの実行を高速化するためのGPUなどのハードウェアの使用をサポートしていること。
- フュージョンなどの様々な最適化をサポートし、フュージョンの動作を高速化するためのライブラリを利用できること。
- インメモリコンピューティングのみを行うが、1台のマシンやクラスタでメモリを使い果たしてしまうと、タスクが失敗してしまうのは避けたい。メモリが不足していても計算が完了できるように、一時的に未使用のデータをディスクなどのストレージにダンプしておく必要があります。
Marsとは何か、何ができるのか?
Marsは、このような問題を解決するためのフレームワークです。現在のところ、Marsにはtensorが含まれています。
100億規模のモンテカルロ法で円周率を計算するタスク規模は150GBとなり、OOMが発生してしまいます。Mars tensor APIを使えば、import numpy as npをimport mars.tensor as mtに置き換えるだけで、その後の計算は全く同じです。しかし、1つだけ違いがあります。mars.tensorはexecuteでトリガーする必要があるため、融合などの中間処理全体をできるだけ最適化できるというメリットがあります。この方法はデバッグにはあまり役に立たないのですが、将来的にはnumpyコードと全く同じようにステップごとに計算をトリガーできるイーガーモードを提供する予定です。
上記のように、この計算時間は並列書き込みと同等で、ピーク時のメモリ使用量は1GBちょっとです。このことから、完全な並列化を実現し、Mars tensorsによってメモリ使用量を節約できることがわかります。
現在、Marsは一般的なnumpyインターフェースの70%を実装しています。完全なリストはこちらを参照してください。私たちは、より多くのnumpyとscipyのインターフェースを提供するために努力してきました。最近では、逆行列計算のサポートも完了しました。
また、Mars tensorsはGPUやスパース行列もサポートしています。 eyeは単位対角行列を作成するために使用されますが、これは対角線上に1の値しか持たず、高密度に保存するとストレージを無駄にします。現在、Marsのテンソルは2次元のスパース行列しかサポートしていません。
Marsで並列化を実現してメモリ使用量を節約するには?
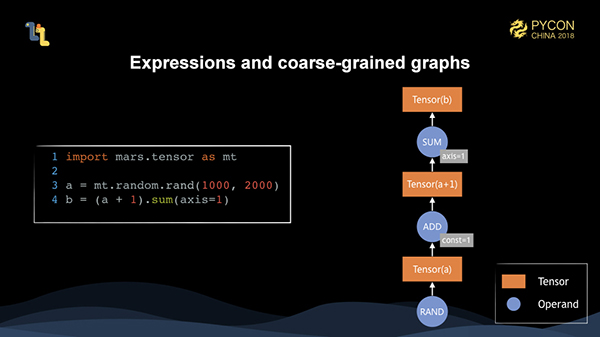
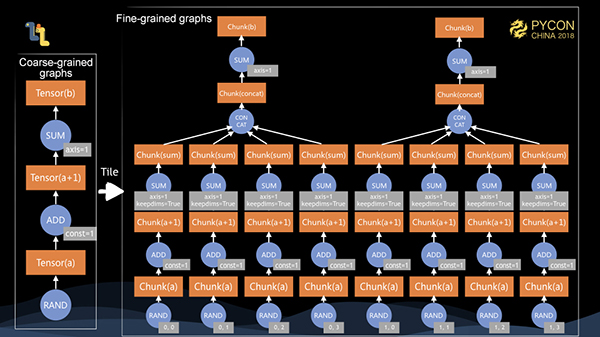
他のデータフローフレームワークと同様に、Marsにも「計算グラフ」という概念があります。違いは、Marsには粗視化されたグラフと微視化されたグラフの概念が含まれていることです。クライアントが書いたコードは、クライアント上で粗視化されたグラフを生成します。それがサーバに送信された後、タイリング処理が行われ、粗視化されたグラフが微視化されたグラフにタイリングされます。そして、微視化されたグラフを実行するようにスケジューリングします。
ここでは、クライアントが書いたコードは、テンソルとオペランドからなる粗視化されたグラフとしてメモリ上に表現されます。
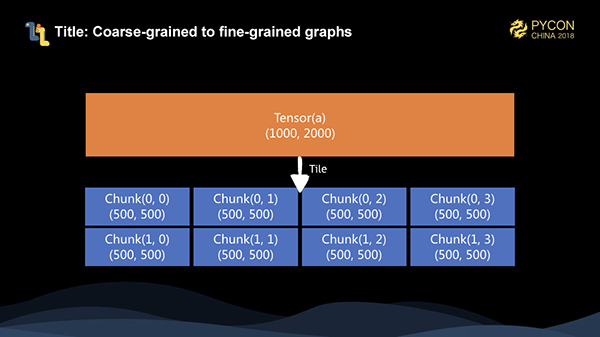
クライアントがexecuteメソッドを呼び出すと、粗視化されたグラフがサーバにシリアライズされます。シリアライズ後、微視的なグラフにタイル化します。10002000 の行列の場合、各次元のチャンクサイズを 500 とすると、24 個のチャンクにタイル化され、合計 8 個のチャンクになります。
その後、実装された各オペランド、すなわち演算子に対して、粗視化されたグラフを微視化するタイリング演算を行います。このとき、スタンドアロンマシンで8コアあれば、細粒化グラフ全体を並列に実行できることがわかる。また、メモリサイズが12.5%であれば、グラフ全体の計算を完了させることができます。
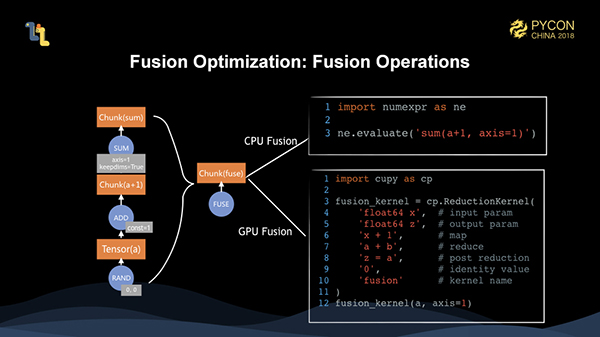
しかし、実際に実行を開始する前に、グラフ全体を融合させているので、融合が最適化されていることになります。実際に3つの演算を実行すると、1つの演算子に融合されます。実行対象が異なる場合は、numexprとcupyのフュージングサポートを利用して、それぞれCPU演算とGPU演算をフュージングして実行しています。
上記の例は、いずれも簡単に並列に実行できるタスクです。先に述べたように、タイリング後に生成される微細なグラフは、実際には非常に複雑です。実世界のコンピューティングのシナリオでは、このようなタスクは実際にはたくさんあります。
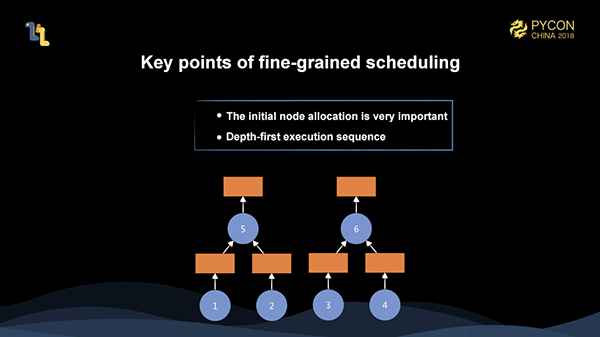
これらの複雑な細粒化グラフの実行を完全にスケジューリングするためには、実行を十分に効率的にするためのいくつかの基本原則を満たさなければなりません。
まず、初期ノードの割り当てが非常に重要です。例えば、上の図の場合、2人のワーカーがいるとします。1と3を1人のワーカーに割り当て、2と4をもう1人のワーカーに割り当てると、5と6がスケジュールされたときに、リモートデータプルのトリガーが必要となり、実行効率が大幅に低下してしまいます。最初に1と2を1人のワーカーに割り当て、3と4を別のワーカーに割り当てると、非常に効率的な実行が可能になります。初期ノードの割り当ては、実行全体に大きな影響を与えます。そのため、より良い初期ノードの割り当てを実現するためには、微細化されたグラフ全体を全体的に把握しておく必要がある。
また、深さ優先実行の方針も非常に重要です。現時点でワーカーが1人しかいないとします。1と2を実行した後に3をスケジュールすると、5がまだ発動していないため、1と2に割り当てられたメモリを解放できません。しかし、1と2を実行した後に5をスケジュールすれば、5の実行後に1と2に割り当てられたメモリを解放することができるので、全体の実行中に最も多くのメモリを節約することができます。
したがって、初期ノード割り当てと深さ優先実行が最も基本的な2つの原則である。しかし、Marsの全体的な実行スケジューリングには難しい課題が多いため、この2点だけでは十分とは言えません。また、長期的に最適化する必要がある対象でもあります。
Mars分散フレームワーク
上述したように、Marsは本質的には、微細粒状の異種グラフのスケジューリングシステムです。細粒化された演算子を様々なマシンにスケジューリングし、実際の実行では、numpy, cupy, numexprなどのライブラリを呼び出します。これらの分野で車輪を再発明するのではなく、成熟した高度に最適化されたスタンドアロンのライブラリをフルに活用しています。
この過程で、いくつかの困難に遭遇するかもしれません。
- マスタースレーブアーキテクチャを使用しているので、マスターが一点になるのをどうやって回避するのか?
- ワーカーはどのようにしてPythonのGIL(Global Interpreter Lock)制限を回避するのでしょうか?
- マスターの制御ロジックは非常に複雑です。高結合で長いコードを簡単に書くことができます。しかし、どのようにしてコードをデカップリングすることができるのでしょうか?
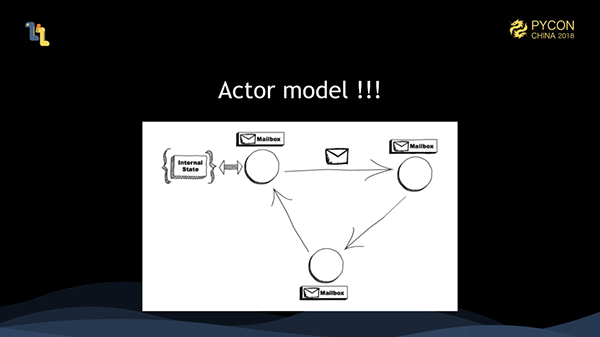
私たちの解決策は、アクターモデルを使用することです。アクターモデルは並列モードを定義します。つまり、すべてがアクターです。各アクターは内部状態を保持し、すべてメールボックスを保持しています。アクターはメッセージを介してお互いに通信します。受信したメッセージはメールボックスに置かれます。アクターは処理のためにメールボックスからメッセージを取得し、1つのアクターは一度に1つのメッセージしか処理できません。アクターは最小の並列単位です。アクターは一度に1つのメッセージを処理できるだけなので、同時実行性を心配する必要は全くありません。並行性はアクターフレームワークで処理する必要があります。また、すべてのアクターが同じマシン上にあるかどうかは、アクターモデルでは無関係になります。アクターモデルは、アクターが異なるマシン上でメッセージ送信を完了できるように、自然に分散システムをサポートします。
アクターは最小の並列単位です。したがって、コードを書くときには、システム全体を多くのアクターに分解し、それぞれのアクターが一つの責任を負うことで、オブジェクト指向プログラミングの考え方と似たように、コードをデカップリングすることができます。
さらに、マスターがアクターに分離された後、異なるマシン上にこれらのアクターを分散させることができるので、マスターはもはや一点ではありません。同時に、これらのアクターは一貫性のあるハッシュに基づいて割り当てられます。将来、スケジューラがクラッシュした場合、アクターを再割り当てし、整合性のあるハッシュに基づいて再作成することで、フォールトトレランスの目的を達成することができます。
最後に、アクターは複数のプロセスで実行され、各プロセスは多数のコルーチンを持っています。このようにして、ワーカーはGILによって制限されることはありません。
ScalaやJavaなどのJVM言語では、アクターフレームワークであるakkaを使用することができます。Pythonの場合は、標準的なプラクティスはありません。akkaが提供する高度な機能の一部を必要としない、軽量なアクターフレームワークであれば、私たちのニーズを満たすことができるはずだと考えています。そこで、軽量アクターフレームワークであるMars actorsを開発しました。Marsの分散スケジューラやワーカーはすべてMars actorsレイヤー上にあります。
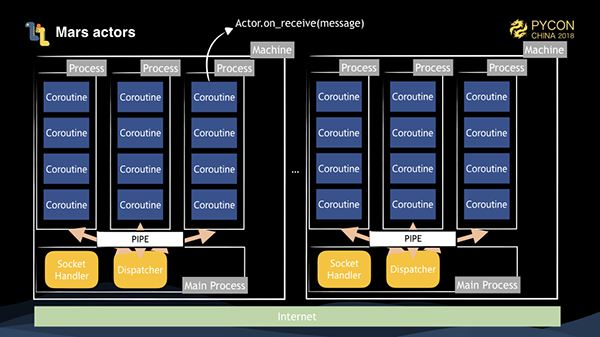
これは、私たちのMarsアクターのアーキテクチャ図です。アクタプールを開始すると、サブプロセスは並行性に基づいていくつかのサブプロセスを開始します。メインプロセスには、リモートソケット接続によって配信されたメッセージを受け付けるソケットハンドラと、メッセージを宛先に応じて配信するディスパッチャオブジェクトがあります。すべてのアクターはサブプロセス上に生成されます。アクターが処理のためにメッセージを受信すると、コルーチンを介して Actor.on_receive(message) メソッドを呼び出します。
あるアクターが別のアクターにメッセージを送信するためには、3つの状況を考慮する必要があります。
1、それらが同じプロセス内にある場合は、コルーチンを介して直接呼び出すことができます。
2、それらがマシン上の異なるプロセスにある場合、メッセージはシリアライズされ、パイプラインを介してメインプロセスのディスパッチャに送信されます。ディスパッチャは、バイナリヘッダ情報のロックを解除することでターゲットのプロセスIDを取得し、対応するパイプラインを介して対応するサブプロセスに送信します。サブプロセスは、コルーチンを介して対応するアクターのメッセージをトリガーにして処理を行うだけである。
3、それらが異なるマシン上にある場合、現在のサブプロセスは、ソケットを介して対応するマシンのマスタープロセスにシリアル化されたメッセージを送信し、マシンはディスパッチャを介して対応するサブプロセスにメッセージを送信する。
コルーチンはサブプロセスの並列メソッドとして使われており、コルーチン自体はIO処理に強い性能を持っているので、アクターフレームワークもIO性能が良いです。
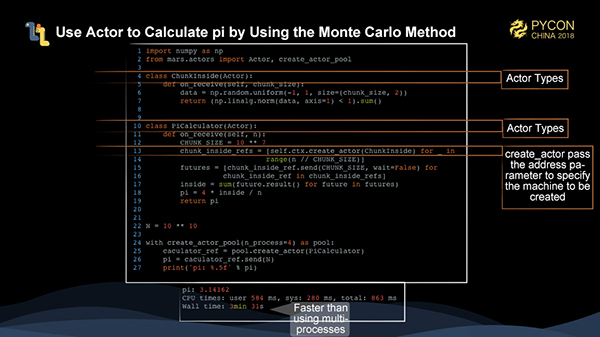
上の図は、Marsのアクターだけを使ってモンテカルロ法でπを計算する方法を示しています。ここでは2つのアクターが定義されています。一つはChunkInsideというアクターで、円の中に落ちてくる点の数を計算するためのチャンクの大きさを受け入れます。もう一つのアクターはPiCaculatorで、ChunkInsideを作成するためのポイントの合計数を受け付ける。この例では、1,000個のチャンクインサイドを直接作成し、メッセージを送信することで計算のトリガーとしています。create_actorでアドレスを指定することで、アクターを異なるマシンに割り当てることができます。
図のように、Marsアクターを使うだけの場合は、マルチプロセスよりもパフォーマンスが速くなります。
まとめると、マーズアクターを使うことで、GILの制約を受けずに分散コードを簡単に書けるようになり、IO効率が向上します。また、アクターのデカップリングによりコードのメンテナンスが容易になります。
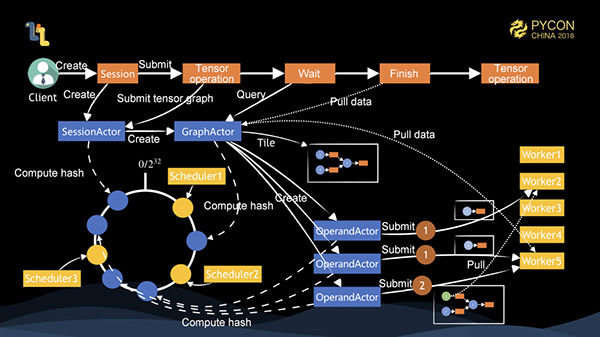
それでは、Marsの完全な分散実行プロセスを見てみましょう。上図のように、クライアントが1つ、スケジューラが3つ、ワーカーが5つあります。クライアントはセッションを作成し、セッションはサーバ上にSessionActorオブジェクトを作成します。このオブジェクトは、一貫性のあるハッシュを介してスケジューラ1に割り当てられます。このとき、クライアントはテンソルを実行する。まず、SessionActorはGraphActorを作成し、粗視化されたグラフをタイル化する。グラフ上に3つのノードがある場合、3つのOperandActorが作成され、それぞれ異なるスケジューラに割り当てられる。各OperandActorは、オペランドの提出、タスクの状態の監視、メモリの解放を制御する。このとき、1と2のOperandActorは、依存関係が見つからず、十分なクラスタリソースがあることが判明した場合、対応するワーカーにタスクを投入して実行させます。実行が完了したら、タスクの完了を3に通知する。データは異なるワーカーによって実行されるため、データの引き抜き動作が先に発動され、タスクを実行するワーカーが決定されてから実行される。クライアントがGraphActorをポーリングしてタスクが完了したことを知ると、ローカルにデータを引っ張る動作が発動する。これでタスク全体が完了します。
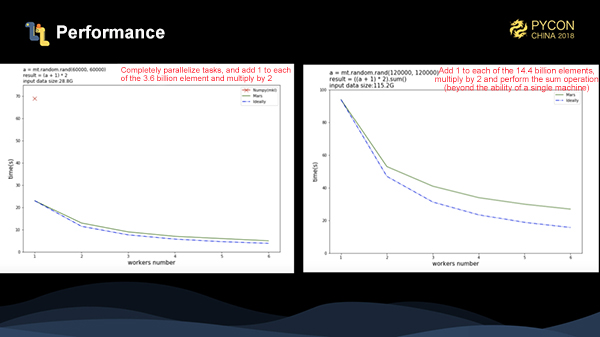
Mars分布のベンチマークを2つ作ってみました。1つ目は、36億エントリのデータの各要素に1を足して2をかけたもので、図中の赤線の部分がnumpyの実行時間です。見ての通り、numpyの数倍の性能を発揮しています。青い点線は理論実行時間であり、実際の加速度は理論時間の加速度に非常に近いことがわかります。2つ目のベンチマークでは、データ量を144億件に増やしました。各要素に1を足して2を掛けたところ、スタンドアロンのnumpyではタスクを完了できないことがわかります。この時点では、このタスクでもそれなりの加速率を得ることができています。
次に何を期待するか?
MarsのソースコードはすでにGithubに投稿されており、より多くの人がMarsの開発に参加できるようになっています: https://github.com/mars-project/mars
上述したように、その後のMars開発計画では、イーガーモードをサポートし、各ステップが実行のトリガーとなり、パフォーマンスに左右されないタスクの開発やデバッグの経験を向上させます。MarsテンソルをベースにGPUもサポートしています;scikit-learn互換の機械学習サポートを提供しています;また、細かい粒度のグラフにカスタム関数やクラスをスケジュールして柔軟性を高める機能も提供しています;最後に、我々のクライアントは実際にはPythonに依存しておらず、どの言語でも粗視化されたグラフをシリアライズすることができるので、ニーズに応じて多言語のクライアント版を提供することができます。
つまり、私たちにとってオープンソースは非常に重要な意味を持っています。巨大なscipy技術スタックの並列化は、私たちだけでは実装できません。興味を持っている皆さんに協力していただき、一緒に構築していく必要があります。
Q&A
最後に、PyConのカンファレンスで発表された共通の質問と回答を紹介したいと思います。大まかにまとめると以下のようになります。
1、MarsはSVD(特異値分解)のようないくつかの特殊な計算を行います。ここでは、クライアントとの協力プロジェクトでのテストデータをいくつか紹介します。入力データは、SVDのための800,000,000 * 32の行列です。SVDが終わったら、元の行列と比較するために乗算を行います。全体の計算処理は100人のワーカー(8コア)を使用し、7分で完了します。
2、Marsがオープンソース化されるのはいつですか?
A: すでにオープンソース化されています: https://github.com/mars-project/mars
3、Marsは後日、クローズドソースに戻されるのでしょうか?
A: いいえ。
4、Marsは静的グラフなのか、動的グラフなのか?
A: 現在は静的グラフです。イーガーモードが終了した後、動的グラフをサポートできるようになります。
5、Marsにはディープラーニングは含まれていますか?
A: 今のところありません。
アリババクラウドは日本に2つのデータセンターを有し、世界で60を超えるアベラビリティーゾーンを有するアジア太平洋地域No.1(2019ガートナー)のクラウドインフラ事業者です。
アリババクラウドの詳細は、こちらからご覧ください。
アリババクラウドジャパン公式ページ