実機で7-qubit codeを実装する【量子ソフトウェア勉強会 GW】

はじめに

量子ソフトウェア開発拠点主催の量子ソフトウェア勉強会で行ったグループワークの内容についてのまとめになります．

7-qubit code (Steane code)とは

スタビライザー符号¹の一つで7つの物理量子ビットで1つの論理量子ビットを構成しており，1つまでのエラーを訂正可能な符号です．Andrew Steaneによって考案²されましたが，後述する状態準備やエラー訂正回路の最適化などが実際の量子コンピュータに対して定量的な有効性を持つかは未だ研究領域にあります．
量子ソフトウェア勉強会ではAmazon Braketを通してIQM Gernet，IonQ Forteでの実装を行いました．

エラー訂正の仕組み

量子回路内でエラー訂正に関わる全ての工程を行うためには，非常に複雑な量子回路が必要になります．3つの工程に分解して紹介します．

状態準備 (エンコード)

スタビライザー符号はいくつかの状態の重ね合わせを論理状態として定義することによってエラーに強い形を保つことができます．しかし，その論理状態を正しく準備できているかを確認する必要があり，この操作をフォールトトレラントに行う量子回路として次の回路が提唱されています³．

8番目の量子ビットは符号化に使われる7つの量子ビットの状態を間接的に測定するために使われます．このような量子ビットをアンシラビットと呼び，7-qubit codeでは状態準備を含めて13以上の量子ビット（訂正回数によってさらに増える）をアンシラビットとして使うことになります．

状態準備の話に戻ると，この回路では測定したアンシラビットが$|0\rangle$であれば，7つの量子ビットは正しく$|0\rangle_L$になったと判断しています．つまり，状態準備のエラー率によっては計算に移ることができる試行回数を減らしてしまうことになります．グループワークでは状態準備のエラー率をシミュレーションと実機の両方で検証しました．

エラー確認回路

論理状態を準備できれば，量子ゲートを使った計算が可能になります．ゲート操作後に本題であるエラーの訂正に移るのですが，古典コンピュータと同様にエラーの場所を特定し，エラーを訂正するという手順を踏みます．したがって，まずはエラー確認回路についてです．量子ビットはエラーの種類がXエラー（フリップエラー），Zエラー（位相反転エラー）の2種類存在するため，それぞれに対してエラーが発生している場所の特定を行う必要があります．エラー確認回路として以下の回路が提唱されています⁴⁵．

1st Flagged

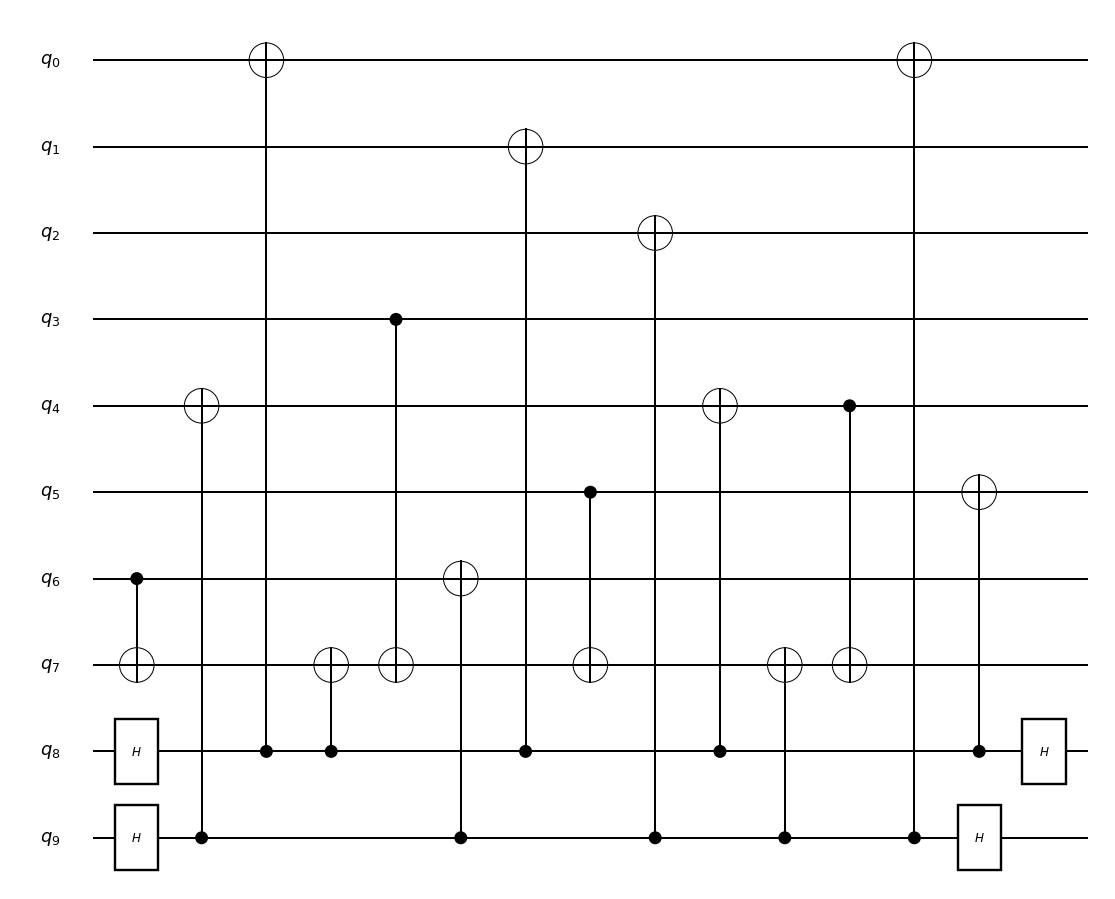
2nd Flagged

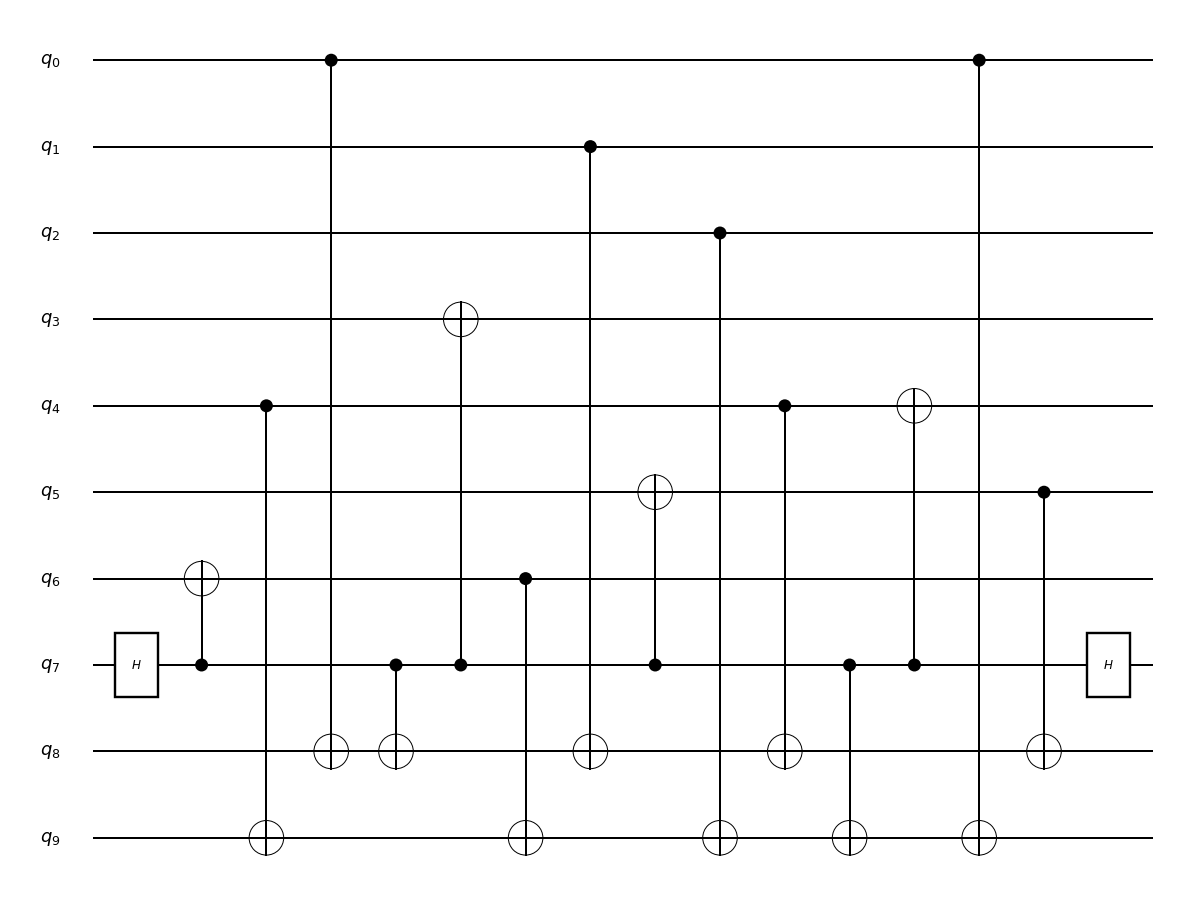
Unflagged-1

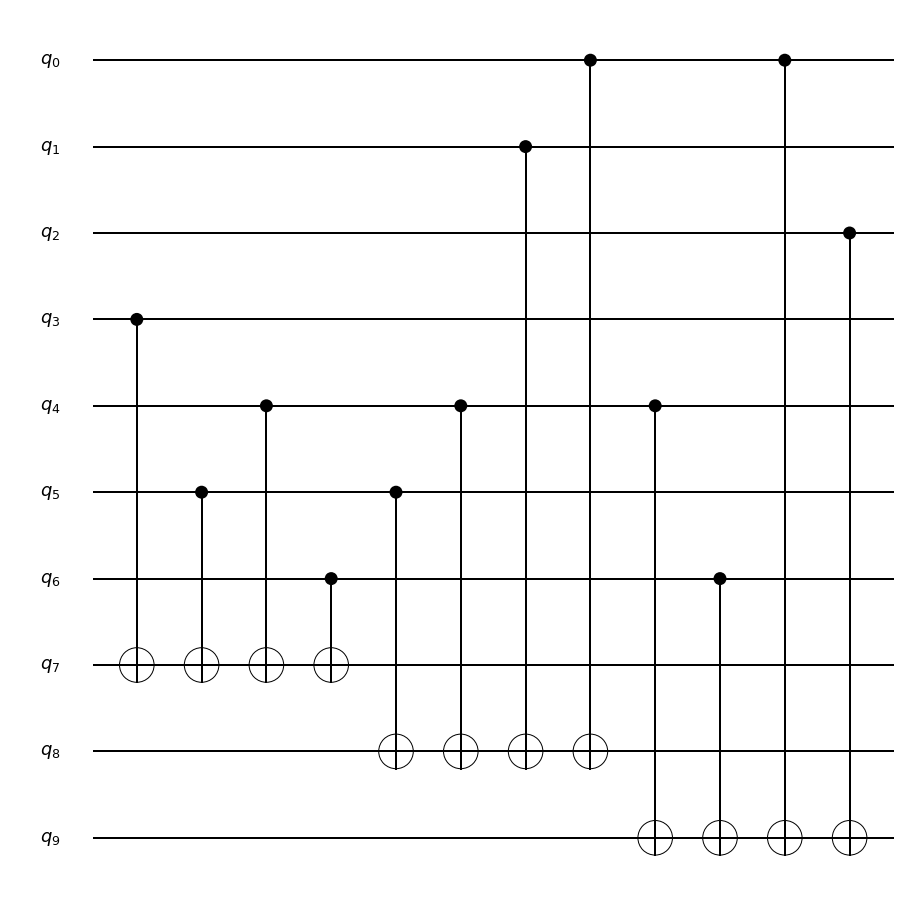
Unflagged-2

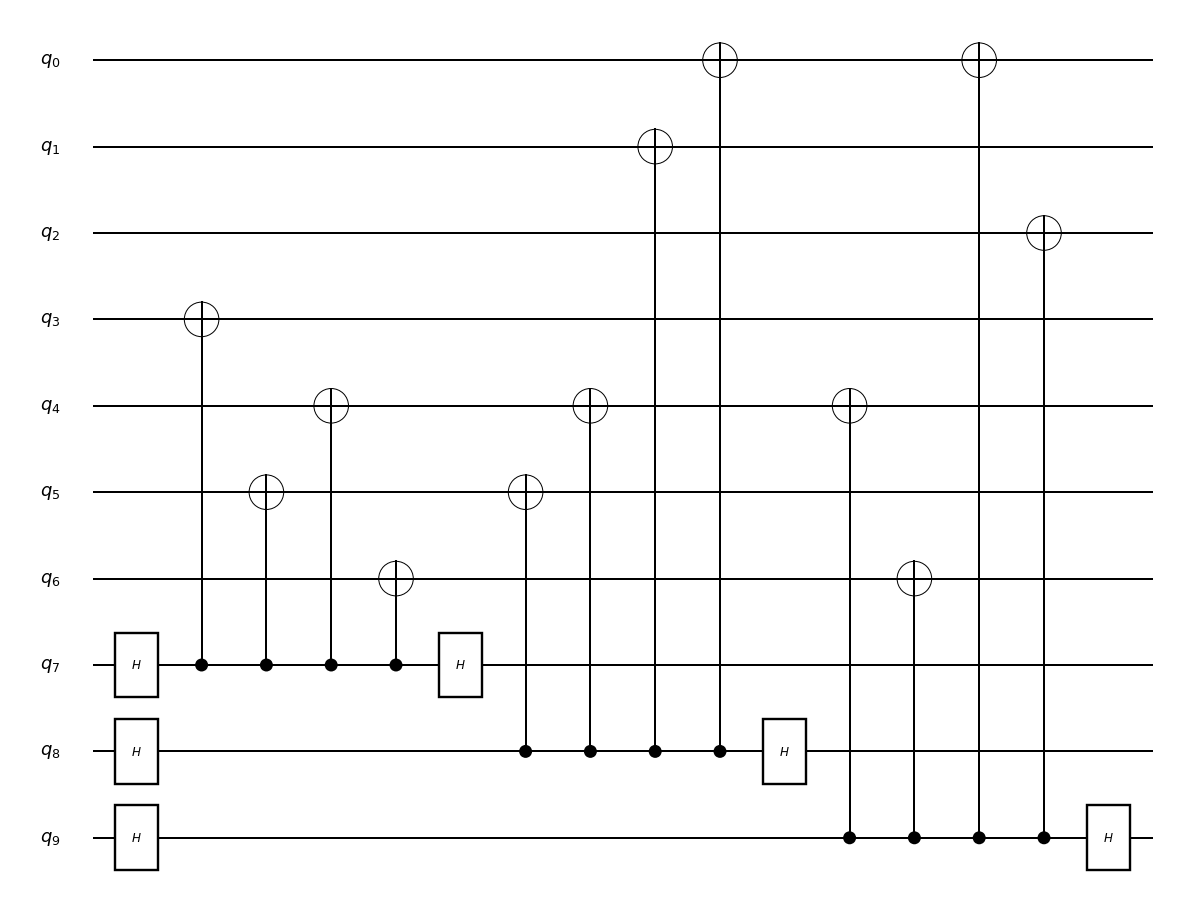
エラー訂正回路

エラーの場所が特定できるとエラー訂正に移るのですが，7-qubit codeは量子回路上でエラー訂正を行うスキームが考案されていないため，エラー確認のアンシラビットの状態かシンドロームの訂正を行います．

グループワークの活動記録

やったことリスト

• シミュレーション (Qulacs)
  • 状態準備
  • エラー訂正
• 実機実装
  • 状態準備
  • エラー訂正

シミュレーション

シミュレーションはQulacs⁶を使って行いました．

状態準備

状態準備のゲート操作に疑似的なエラーを入れることで，状態準備のエラー率の変化をシミュレーションしています．また，フォールトトレラントに状態準備ができたかの検証として，測定後にエラーが発生している量子ビットを1つだけ訂正するコードを追加しています．

もう少し低いエラー率の範囲でプロットすると...

この結果から物理エラー率が4.5%までであれば，フォールトトレラントに状態準備できることが分かりました．

エラー訂正

qiskitでの疑似コード⁵をqulacsに書き換えてシミュレーションを行いました．

エラー訂正回路（QEC）を使うことによってエラー率の減少が分かりました．

実機実装に向けて

実機はAmazon Braketを通してIQM GarnetとIonQ Forte1を使用し，$|0\rangle_L$準備と$|0\rangle_L$にQECを一回かけた際のエラー率の評価を行いました．

いよいよ実装！

キャリブレーションデータ

	2Q エラー	読み出しエラー
IQM Garnet	0.011	0.028
IonQ Forte 1	0.012	0.004

結果

	IQM Garnet	IonQ Forte 1
$|0\rangle_L$	0.025	0.00384
(QEC)$|0\rangle_L$	0.203	0.29

分かったこと

$|0\rangle_L$の状態準備ではどちらの実機も読み出しエラーに大きく影響されていると考えられる結果が得られました．特にIonQ Forte 1では2Qエラーを下回っており，フォールトトレラントな状態準備になっていることが分かりました．
QECをかけた際の結果ではどちらの実機でも大きく2Qエラーを上回ってしまっているため，現在の量子ビットのエラー率では長い量子回路によって蓄積されたエラーはQECで軽減できなかったと考えられます．

感想

約半年にわたるグループワークの中で量子コンピュータのソフトウェアについて多くの学びを得ることができました．主にハードウェアについて研究している自分にとってエラー率⁷の軽減は重要な課題ですが，実機での実行結果からも低い論理エラー率を達成するためにはさらに低い物理エラー率が必要であることが分かりました．

1. スタビライザー符号：スタビライザー群によって符号化されている符号のこと ↩

2. Steane, A. M. Error Correcting Codes in Quantum Theory. Phys. Rev. Lett. 77, 793 (1996). https://doi.org/10.1103/PhysRevLett.77.793 ↩

3. Goto, H. Minimizing resource overheads for fault-tolerant preparation of encoded states of the Steane code. Sci Rep 6, 19578 (2016). https://doi.org/10.1038/srep19578 ↩

4. Postler, L., Heuβen, S., Pogorelov, I. et al. Demonstration of fault-tolerant universal quantum gate operations. Nature 605, 675–680 (2022). https://doi.org/10.1038/s41586-022-04721-1 ↩

5. Ryan-Anderson, C., Bohnet, J. G., Lee, K. et al. Realization of Real-Time Fault-Tolerant Quantum Error Correction. Phys. Rev. X 11, 041058 (2021). https://doi.org/10.1103/PhysRevX.11.041058 ↩ ↩²

6. グループワークで使用したバージョンはQulacs 0.6.10 ↩

7. ハードウェアではすべてのエラーを総じて忠実度というパラメータで評価することが多いです ↩