xy座標に自由に与えられた制御点をスプライン補間する際、使用する関数によっては座標値の増減傾向(正方向、負方向への変異)が制限されます。スプライン補間やscipyライブラリ内の関数の使い方などを復習するついでに、記事として残したいと思います。
スプライン補間とは
簡潔に言うと、座標系に与えられたいくつかの点をスムーズな線で結ぶことです。主な用途としては、離散的なグラフの補間などが挙げられます。
spline を辞書で調べると、「与えられたいくつかの点をなめらかに結ぶ曲線 またそれを表わす関数」と説明されています。「それを表す関数」とは、区分多項式のことでしょう。更にWikipediaで調べてみると、「(金属や木の板などの)弾性変形を利用して、自然な曲線を得る」という例を用いて、特徴が記述されています。
上記のような定義・特徴を持つスプライン曲線ですが、コンピュータグラフィックスの世界では、主にB-spline(Basis-spline)曲線が採用されるようです。Basisはそのまま「基底」を意味しており、ノットベクトルから定義される基底関数にあたります。この辺(区分多項式の導出手法)に関しては、数学的理解を深めるためにもそのうち一つの記事としてまとめたいと思います。
n次スプライン補間
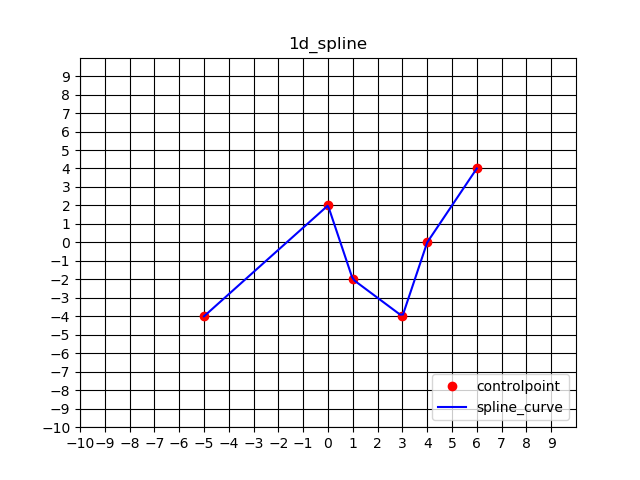
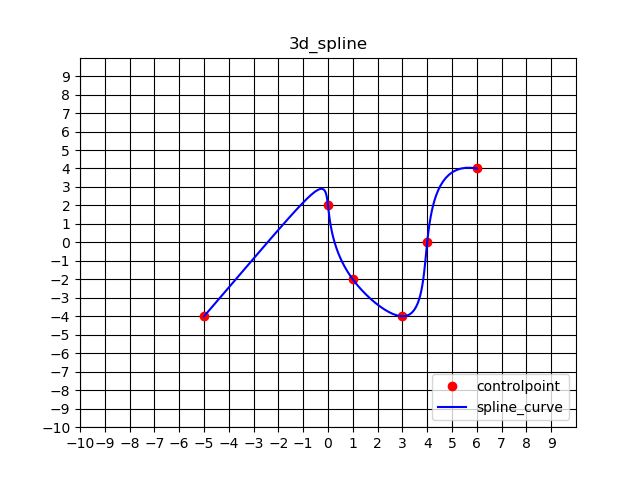
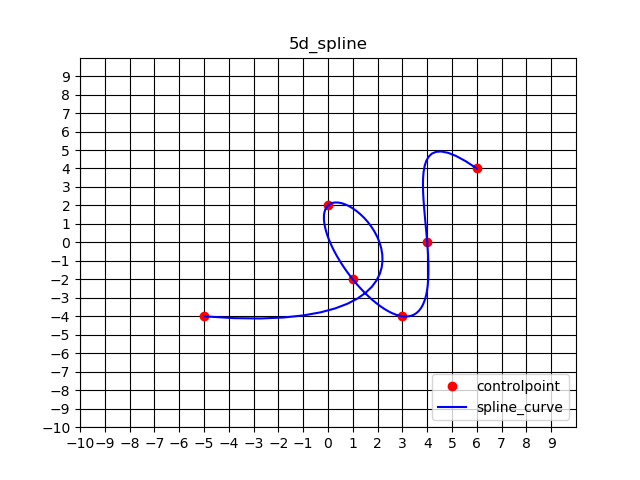
「スプライン補間 python」といった感じで検索すると、多くは「3次スプライン補間」に関する解説記事や備忘録が出てくるかと思います。n次スプライン補間のnは、「与えられた点を通る線の滑らかさ」のことです。この「与えられた点」ですが、以降は制御点(controlpoint)と呼びます。下に示すように、係数nの値が増えれば増えるほど線は滑らか、というか丸みを帯びていきます。
「○d-spline」の○が次数に当たります。1次では直線ですが、3次、5次と次数の増加に伴って線がより滑らかになり、制御点を通過する際の不自然さが無くなっています。
(ちなみにdはdegreeです。○次という字面から、しばらくdimensionのdとして使ってました・・・)
scipyを使ったスプライン補間
scipyが提供するスプライン補間クラスinterpolateには、様々な補間法が関数として定義されています。
今回は以下の三つの関数を使ってみます。Hiroto A様のPython で 1 変量データ補間を参考にさせていただきました。
【interp1d】
f = interpolate.interp1d(x, y,kind="cubic")
-
入力
-
x,y:座標値を要素とするリスト。関数に次数の概念が存在するとき、それぞれの要素数は次数を上回る必要があります。
-
kind:補間手法を指定します。一次ならslinear、二次ならquadraticというように、様々な手法がサポートされています。詳しくは scipy.interpolate.interp1d を参照。今回はcubicで3次補間を指定しました。
-
戻り値
-
f(x):スプライン曲線を表現する関数(区分多項式)を返します。
【Akima1DInterpolator】
f = interpolate.Akima1DInterpolator(x, y)
-
入力
-
x,y:interp1dと同様です。
-
戻り値
-
f(x):interp1d同様、スプライン曲線を表現する関数(区分多項式)を返します。
【splprep】
tck,u = interpolate.splprep([x,y],k=3,s=0)
-
入力
-
x,y:interp1dと同様です。
-
k:次数を決定します。値の範囲は、1<=k<=5です。
-
s:線の滑らかさを調整できます。入力する座標値を基に最適なsの値を計算できるようですが、今回は0に設定しています。詳しくは scipy.interpolate.splprep を参照。
-
戻り値
-
tck:ノットベクトル(=t)、B-spline係数(=c)、次数(=k)を含むタプル。
-
u:scipyのリファレンスには An array of the values of the parameter. と記述されています。値を覗けば察しがつきますが、「与えたパラメータ(x,y)が、生成されたスプライン曲線上のどこに存在しているか」を0~1の割合として示されています。
Code
ではさっそくこれらを使ってスプライン曲線を表現します。
まずは必要なライブラリをインポート
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
先ほどの3つの補間法を関数化しました。
【interp1d】
def spline1(x,y,point):
f = interpolate.interp1d(x, y,kind="cubic")
X = np.linspace(x[0],x[-1],num=point,endpoint=True)
Y = f(X)
return X,Y
【Akima1DInterpolator】
def spline2(x,y,point):
f = interpolate.Akima1DInterpolator(x, y)
X = np.linspace(x[0],x[-1],num=point,endpoint=True)
Y = f(X)
return X,Y
【splprep】
def spline3(x,y,point,deg):
tck,u = interpolate.splprep([x,y],k=deg,s=0)
u = np.linspace(0,1,num=point,endpoint=True)
spline = interpolate.splev(u,tck)
return spline[0],spline[1]
全てのメソッドに、座標値のほかpointというパラメータを導入しています。numpy.linspaceを使い、生成されたスプライン曲線中のx座標点を等間隔に任意数取得するためです。~~当然生成されたスプライン関数に影響を与えることはありませんが、~~プロットされるスプライン曲線を滑らかにするのが狙いなので、入力する座標の要素数よりはるかに大きい値を入れることを推奨します。
splprepで導入しているdegはdegree、次数を示し、kの値を指定します。実際にはsplprepでスプライン補間を行っているというわけではなく、splprepによって補間用のパラメータを生成し、その値をsplev関数に与えることで補間を行っています。
適当にサンプルデータを作りましょう。
x = [-5, 0, 1,3,4,6]
y = [-4, 2, -2,-4,0,4]
作ったメソッドをそれぞれ呼び出します。pointは適当に100を指定しました。
a1,b1 = spline1(x,y,100)
a2,b2 = spline2(x,y,100)
a3,b3 = spline3(x,y,100,3)
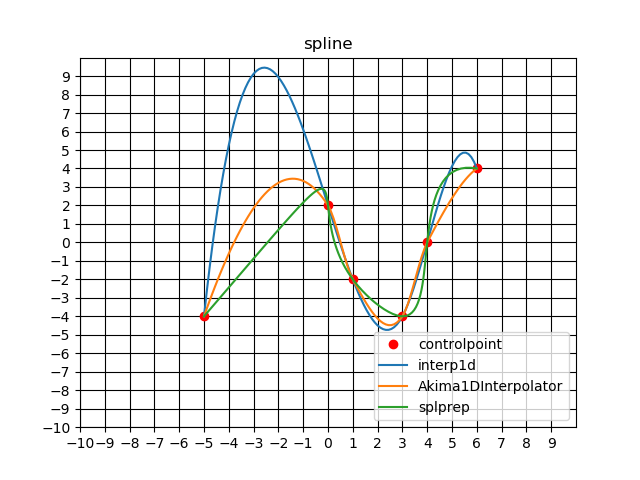
プロットしてそれぞれの結果を見ます。
plt.plot(x, y, 'ro',label="controlpoint")
plt.plot(a1,b1,label="interp1d")
plt.plot(a2,b2,label="Akima1DInterpolator")
plt.plot(a3,b3,label="splprep")
plt.title("spline")
plt.xlim([-10, 10])
plt.ylim([-10, 10])
plt.legend(loc='lower right')
plt.grid(which='major',color='black',linestyle='-')
plt.grid(which='minor',color='black',linestyle='-')
plt.xticks(list(filter(lambda x: x%1==0, np.arange(-10,10))))
plt.yticks(list(filter(lambda x: x%1==0, np.arange(-10,10))))
plt.show()
結果
どれがいいかは一概には言えないですが、個人的にsplprepが自然にフィットしている気がします。
今回与えた点は、x座標に関して増加傾向にあります。では、x座標に関して自由な点が与えられた場合はどうなるか見てみます。
まずは座標を与えます。
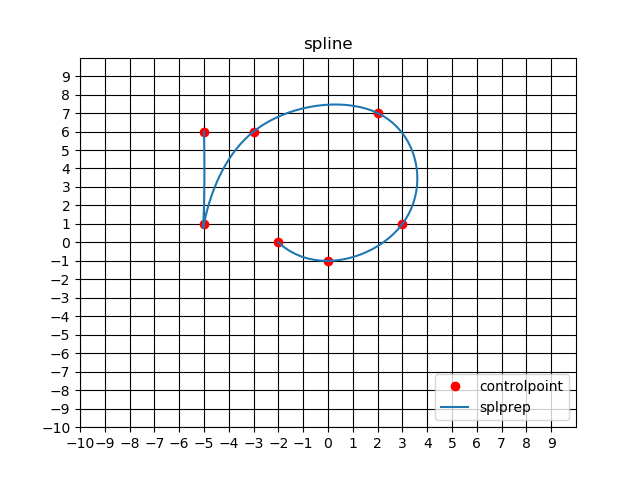
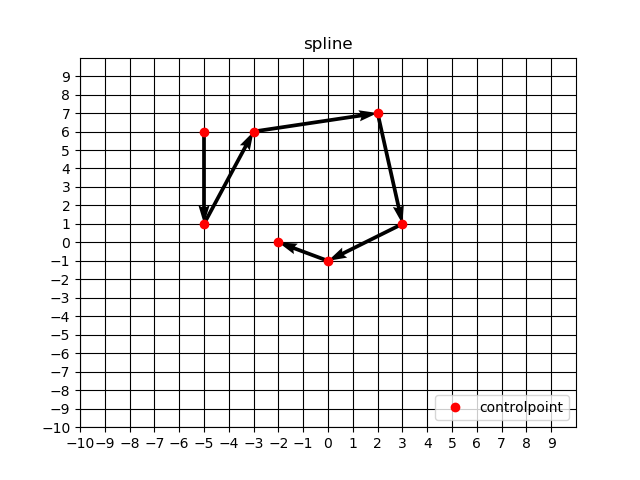
x = [-5, -5, -3, 2, 3, 0, -2]
y = [6, 1, 6, 7, 1, -1, 0]
x座標に関して、重複や減少傾向(負方向への変異)をつけてみました。グラフで見ると↓のようになります。
これをinterp1dでスプライン補間しようとすると、以下のようなエラーが出ます。
ValueError('Expect x to be a 1-D sorted array_like.',)
一方向的な座標変化にしろってことだと思います。
続いてAkima1DInterpolator。
ValueError('x must be strictly ascending',)
こちらもエラーが出ました。x座標に関して増加傾向である必要があるそうです。
エラーは出ず、綺麗にスプライン補間されました。
関数の戻り値の違いによりこうした結果が生じます。
他二つの関数とは違い、splprepはスプライン曲線上にある制御点の場所u及びタプルtckを返します。パラメータuが他の関数で言うところのx座標のようなもに当たるのだと思いますが、あくまでuはスプライン曲線上の場所を示すのみなのでx座標の変異に左右されないのだと思います。
まとめ
今回はスプライン補間のための関数を3つ動作させ、出力の違いをまとめてみました。
3つの中では、変異が単一方向でない自由な制御点が与えられた場合はsplprepを使うのがよさそうです。
そもそもスプライン補間は、「統計的なグラフ上の離散点同士を繋ぐ」ような目的で利用される場合が多いのかもしれません。今回利用したコードは以下に載せておきます。
# 三つのスプライン補間法
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
# interpld
def spline1(x,y,point):
f = interpolate.interp1d(x, y,kind="cubic") #kindの値は一次ならslinear、二次ならquadraticといった感じに
X = np.linspace(x[0],x[-1],num=point,endpoint=True)
Y = f(X)
return X,Y
# Akima1DInterpolator
def spline2(x,y,point):
f = interpolate.Akima1DInterpolator(x, y)
X = np.linspace(x[0],x[-1],num=point,endpoint=True)
Y = f(X)
return X,Y
# splprep
def spline3(x,y,point,deg):
tck,u = interpolate.splprep([x,y],k=deg,s=0)
u = np.linspace(0,1,num=point,endpoint=True)
spline = interpolate.splev(u,tck)
return spline[0],spline[1]
if __name__ == "__main__":
#x座標に関して、重複、減少傾向を持つ座標群
#x = [-5, -5, -3, 2, 3, 0, -2]
#y = [6, 1, 6, 7, 1, -1, 0]
#x方向に増加傾向である座標群
x = [-5, 0, 1,3,4,6]
y = [-4, 2, -2,-4,0,4]
a1,b1 = spline1(x,y,100) #interp1dメソッドを実行
a2,b2 = spline2(x,y,100) #Akima1DInterpolatorメソッドを実行
a3,b3 = spline3(x,y,100,3) #splprepメソッドを実行
#グリッド線やラベルなどを付与しつつスプライン曲線をプロット
plt.plot(x, y, 'ro',label="controlpoint")
plt.plot(a1,b1,label="interp1d")
plt.plot(a2,b2,label="Akima1DInterpolator")
plt.plot(a3,b3,label="splprep")
plt.title("spline")
plt.xlim([-10, 10])
plt.ylim([-10, 10])
plt.legend(loc='lower right')
plt.grid(which='major',color='black',linestyle='-')
plt.grid(which='minor',color='black',linestyle='-')
plt.xticks(list(filter(lambda x: x%1==0, np.arange(-10,10))))
plt.yticks(list(filter(lambda x: x%1==0, np.arange(-10,10))))
plt.show()
♯追記
2020/01/30 splevに関する説明を追記しました。