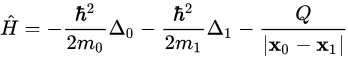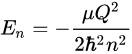量子力学への入り口はあちこちにありますが、ここでは比較的身近に感じられる**「光」についての学問、つまり光学を入り口に選んでみましょう。そのためにはまず、光学で頻繁に使われる道具である「プリズム」**について知っておく必要があります。プリズムは均質な水晶やガラスで出来た透明な多面体で、太陽光が入射されると虹のような模様を吐き出します。ピンと来ない人は、ピンク・フロイドの Dark Side of the Moon のジャケットを見ましょう。

出典:amazon.co.jp
プリズムが「太陽光から虹を作る」こと自体は古くから知られていて、紀元一世紀頃にはローマのセネカやプリニウスが著作の中で報告しています。しかし、これを**「色ごとに屈折率が異なるため、光が分解されてる」と見抜いたのは17世紀の錬金術師ニュートンでした。ニュートンはプリズムから出てくる光の模様をスペクトル**と名付けました(ラテン語で幻像という意味で、幽霊を意味する英語スペクターの語源です)。ニュートンは複数のプリズムを使った実験によって、スペクトルを構成する一つ一つの単色光を抜き出してプリズムを通しても色が変わらないこと、またこれら単色光を合成することで元の白色光が作れることを発見しました。

出典:Public Lab
さて、太陽光のスペクトルをよく見てみると、幾つかの暗い線が**「飛び飛び」に現れているのがわかります。この暗い線がフラウンホーファー線と呼ばれることは、高校の理科で習ったかもしれません。フラウンホーファー線の存在は、「太陽光には特定の色の光が含まれていない」**ことを意味しています。
せっかちな人のために答えを教えておくと、実はこの**「飛び飛び」の犯人が、量子力学における固有値問題**です。
他にも「飛び飛び」のスペクトルの例があります。ガラス管に水素を封入して電圧をかけると、パチンコ屋のネオンサインと同じ原理で光ります。この水素放電管の光をプリズムに通すと、太陽のような虹色ではなく、幾つかの明るい線が「飛び飛び」に現れるだけです。これは**「水素が特定の色の光しか出さない」ことを意味しています。似たような実験を他の原子ですると、やはり原子ごとに特定の色しか出さないことがわかります。この現象を利用したのが花火**です。金属原子の炎色反応から出る光が原子ごとに異なるため、色とりどりの花火を作ることができるわけです。
興味深いのは、水素スペクトルにおける「飛び飛び」の明るい線は、先ほどの太陽光スペクトルにおける「飛び飛び」の暗い線の一部と、位置がピッタリ重なるということです。さらに、水素スペクトルと一致しない残りのフラウンホーファー線も、酸素やナトリウムなど、他の原子が出すスペクトルと一致します。なぜこんなことが起こるのでしょうか?

出典:わかりやすい高校物理の部屋
この不思議な一致は、原子の「出せる色」と「吸収できる色」が同じであるために起こります。「原子がどの色を吸収できるか」は、太陽光の代わりに白熱電球を光源として、プリズムの前に原子を置いた場合と置かない場合のスペクトルを比較すれば、実験的にちゃんと確かめられます。つまりフラウンホーファー線とは、光が太陽から発せられて地上に辿り着くまでの間、様々な原子にぶつかったために吸収されてしまった色なのです。
では、なぜ、原子は特定の色だけを吸収したり放出したりするのでしょうか? 物理学者のニールス・ボーアは次のような仮説を考えました。原子核の周りでは電子が回っている。この電子が取りうる軌道は、「飛び飛び」であるに違いない。そして、それぞれの軌道は**「固有のエネルギー」を持っている**。電子が**「高いエネルギーの軌道」から「低いエネルギーの軌道」に移るときは、エネルギーが放出されて光となる。逆に、電子が「低いエネルギーの軌道」にいるときは、光を吸収することによって、「高いエネルギーの軌道」に移ることができる。結局、この「各軌道に固有なエネルギー」の差**だけによって、その原子が放出・吸収できる光の色が決まっているのだ。
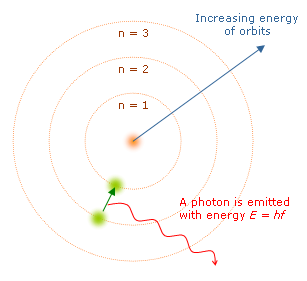
出典:Wikipedia「ボーアの原子模型」
実際、ボーアの仮説によって、水素原子のスペクトルに見られる規則性(リュードベリの公式)をとてもうまく説明できました。残る問題は、**「なぜそもそも電子の取りうる軌道/エネルギーは、『飛び飛び』なのか」ということです。別に連続でもいいはずの物理量が、なぜ「飛び飛び」になってしまうのか。この性質をカッコよく言うと、「量子性」**という言葉になります。量子力学とは、量子性を説明するために生まれた学問です。次に量子力学の概要を簡単に説明します。
量子力学の大きな特徴のひとつは、**「我々が測れる量はすべて確率的に値が決まっている」**と考える点です(この考えに反対したアインシュタインは「神はサイコロを振らない」という名言を残しました)。つまり、まったく同じ状態の系を二つ用意しても、それぞれの系で測定値が変わりうることを認めます。一体、そんなあやふやな世界でどのような理論を作ることが出来るのでしょうか? なんと、それまでの物理学のように物理量の測定値を直接予言することは諦めて、物理量の測定値の「確率分布」を予言することに方針を変えるのです。

出典:John C. Holden's Unpublished T-shirt design
量子力学にもいろいろ流儀があるのですが、ここで紹介するのはシュレディンガー式の量子力学です。大雑把に言うと、シュレディンガー描像の量子力学では、測定値の**「確率分布」は、時間発展する「状態」と、時間発展しない「物理量」**の掛け算で得られます(ボルンの規則)。ここでいう「状態」や「物理量」は、常識的な=古典力学的な意味での状態や物理量とは異なる概念です。
量子力学の**「状態」とは波動関数と呼ばれる複素数の無限次元ベクトルで、その時間発展はシュレディンガー方程式**
i \hbar \frac{\partial}{\partial t} \psi = \hat{H} \psi
によって定められます。ここで $\psi$ が波動関数、 $\hbar$ は定数、 $\hat{H}$ は後に述べる**ハミルトニアンという「物理量」です。ボーアの考えていた「電子の取りうる軌道」**というのも、その実体は量子力学的な状態のことで、波動関数に対応します。原子核の周りを電子が「回っている」というのは古典力学の考えで、量子力学からすると正しくないのですが、それでも歴史的な経緯とわかりやすさから、電子の取りうる状態=波動関数を「軌道」と呼んだりします(英語では古典力学の軌道をorbit、量子力学の軌道をorbital、つまり"軌道のようなもの"と呼んで、微妙に区別がつけられています)。
量子力学の**「物理量」とはオブザーバブル**(可観測量)と呼ばれる複素数の無限次元行列(線形作用素、演算子)で、その固有値が**「取りうる測定値」になっています。それぞれの測定値=固有値の出る確率は、先に述べたようにボルンの規則によって定められます。具体的には、固有ベクトルに現在の波動関数を掛け算して自乗したものが、対応する固有値の出る確率となっています。ところで、我々が観測する物理量の測定値は実数に限られるため、物理量はエルミート行列**(対称行列の複素数版)であるべきです。そんな都合の良い行列をどこから持ってくるのでしょうか? 幸い、古典力学の「物理量」から量子力学の「物理量」を天下り的に得る正準量子化という手法があります。状態の時間発展を表すシュレディンガー方程式に含まれていたハミルトニアン $\hat{H}$ もエルミート行列ですが、これは古典力学でいうところのハミルトニアン(全エネルギー) $H$ を正準量子化して得られるものです。
さて、時間的変化がない状態(定常状態)を仮定すると、シュレディンガー方程式は $E$ を定数として、固有方程式
\hat{H} \psi = E \psi
の形になります。つまり定常状態の波動関数はハミルトニアンが持ついずれかの固有ベクトルになります。ボルンの規則から、定常状態で観測されるエネルギーは、この固有ベクトルに対応する固有値 $E$ 以外ありえません。ハミルトニアンの固有値をエネルギー固有値と呼びます。波動関数が無限遠でゼロになるという条件を入れると、一般的にエネルギー固有値は離散的になります。ボーアの言っていた電子の取りうる軌道が**「飛び飛び」**になるという現象は、実はこのエネルギー固有値の離散性に由来しているのです。
具体例として、最も単純な構造の原子、つまり、ひとつの陽子(正電荷)の周りをひとつの電子(負電荷)が回っている水素原子のハミルトニアンと、そのエネルギー固有値を書き下しましょう(なお、最も簡単な水素原子ですら、シュレディンガー方程式を手で解くのはかなり骨が折れ、その解き方はもはや芸術の域です):
出典:Wikipedia「水素原子におけるシュレーディンガー方程式の解」
この水素原子のエネルギー固有値$E_n$は、まさにボーアの原子模型と同じもので、ちゃんと水素原子のスペクトル系列を説明することができます。こうして、太陽光のスペクトルに現れる「飛び飛び」の暗い線は、量子力学の固有値問題までその起源を遡ることができるのでした。毎日浴びる陽の光の中にも固有値問題が潜んでいるというのは、なかなかに面白い気がします。
……いやいやいやちょっと待て、なんだよこのシュレディンガー方程式とかいうの、そもそもこの式はどっから出てきたんだよと思った方向けに、ファインマン先生のありがたいお言葉をお送りして、この記事の〆としたいと思います。
どこからこれが得られたのか。どこからでもない。これを諸君の知っていることから導き出すことは不可能である。これはシュレーディンガーの精神から生まれたものである。