現代はビッグデータの時代と言われて久しいですが、「データが大きい」と一口に言っても、2種類の大きさがあります。データの次元と**サンプルサイズ(N数)**です。例えば、「全人類の身長と体重のデータ」なら「次元が小さいけどNが大きいデータ(次元は2、N=70億)」ですし、「10人分のゲノム配列データ」なら「次元が大きいけどNが小さい(次元は60億、N=10)」と言えるでしょう。
サンプルサイズがデータの次元より小さいというのは、一般的にデータが不足している状況であり、あまり好ましくありません。たとえば変数の間にある関係を捉えることが難しくなります(回帰における劣決定問題)。
しかし、多次元・多変数のデータにおいて、すべての変数が意味を持つということも稀です。幾つかの変数は単に「意味を持たないただのノイズ」だったりします。ゲノムの例でいうと、ヒトゲノムのおよそ97%は無意味なジャンクDNAであると言われているので、60億ある塩基配列のすべてを解析に用いる必要はないかもしれません(実際に何割がジャンクDNAなのかというのは議論の余地が在るところです)。一般論として、もしも解析の目的と無関係な変数が事前にわかっていれば、そういった変数は解析の前に削除しておくほうがよいでしょう。
データの次元を減らすためには、単に変数を削除するだけではなく、変数をまとめるということも考えられます。変数の間に強い相関がある場合(回帰分析では多重共線性と呼ばれる)、それらは実質的にひとつの変数としてみなせます。ゲノムの例だと、塩基配列ではなく遺伝子という機能単位で見れば、60億から2万程度の次元に落とせます。さらに、ゲノム上の距離が近い遺伝子は同時に遺伝されやすいという現象(遺伝的連鎖)のおかげで、特定の遺伝子の組み合わせ(ハプロタイプ)をまとめてひとつの変数とみなすこともできます。
つまり、一見すると多次元すぎて手に負えないようなデータでも、あらかじめ注目するべき変数(特徴)を知っていれば、データの次元を絞り込め、現実的なデータ解析が可能になる、ということです。とはいえ、上記のように対象分野についての事前知識がある場合は良いですが、そのような事前知識がない場合はどうやって特徴を見つければよいのでしょうか? こういうときに用いられる統計的手法を、次元削減や特徴抽出と呼びます。機械学習でいうと、ラベルなしのデータから隠れた構造を見つけ出す教師なし学習に分類されます。
今回ご紹介する主成分分析(PCA; Principal Component Analysis)という手法は、次元削減の最も簡単な手法です。最も簡単でありながら、広い分野で現役で使われている手法です。あまりにも簡単なので、統計学と線形代数の基礎さえ知っていれば、次の一言で説明が終わります:分散共分散行列の固有ベクトルを取る。分散共分散行列というのは、変数同士のばらつき関係をまとめた表(※)であり、幾何学的に言えばデータのばらつきの大きさと向きを表しています。この行列の固有ベクトルを取るということは、データがよくばらついている方向に合わせて空間の軸を取り直すということです。
(※……分散共分散行列を無次元化したものが相関行列です。ここでいう次元というのは、「データの変数の数」という意味の次元ではなく、「各変数が持つ単位(キログラムとかメートルとか)」という意味の次元です。異なる次元(単位)の混ざったデータに対しては、分散共分散行列ではなく相関行列を使って主成分分析を行うのが普通です)
主成分分析における固有値は、その固有ベクトルの方向に沿ったデータの分散の大きさに対応します。固有値が大きい固有ベクトルほど、データの分散をよく説明している、つまり、データの重要な特徴を捉えていると考えられます。なので、各固有値を固有値の合計で割ったものを寄与率と呼んだり、固有値(寄与率)が大きい主成分から順に、第1主成分(PC1)、第2主成分(PC2)……と呼んだりします。実際の問題では、元々の次元が1万以上あっても、固有値が大きい2~3個の固有ベクトル(主成分)だけでデータの8割を説明できることも珍しくありません。そして大体、主成分には何かしらの「意味」を見出せる、というか、後付けで解釈できることが多いです。
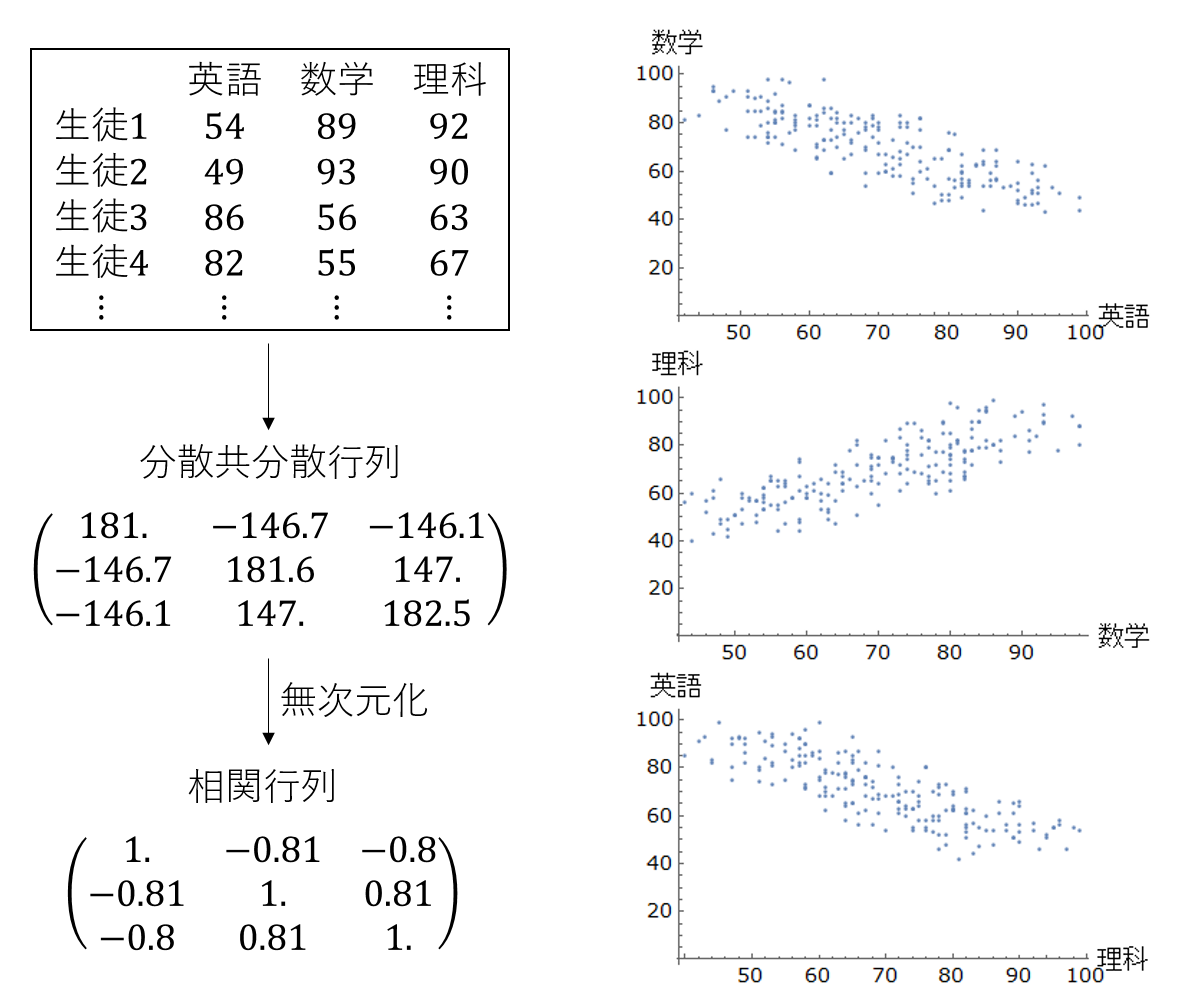
実例を示しましょう。ある高校のある学年に200人の生徒がいるとします。この学年で、100点満点のテストを英語・数学・理科という3つの科目それぞれについて行いました(次元は3,N=200)。得られた結果(表、分散共分散行列、相関行列、二次元の散布図)は次のようなものになりました。
このデータに対して主成分分析を施し、得られた主成分(固有ベクトル)を矢印として三次元散布図に重ねたものが次の図です。一方向からの視点からだけだとわかりにくいので、2つの視点から描きました。固有ベクトルというのは大きさ1ですが、ここではそれぞれの主成分の重要度の違いを表現するため、矢印の大きさに寄与率(固有値)の大きさを対応させています。

この図で「軸を取り直す」ということのイメージと、その有用性がわかるかと思います。第一主成分(PC1)の寄与率は87%であり、データのばらつきがほぼこれだけで説明できています。つまり、実質的に3次元のデータを1次元に落とし込むことができたわけです。繰り返しになりますが、主成分分析とは単に軸を取り直す=新たな直交座標系を作る作業にすぎません(分散共分散行列は対称行列であるため、固有ベクトルが直交します)。しかしその後で人間が寄与率(固有値)の大きい主成分(固有ベクトル)だけに注目することで、実質的にデータの次元をぐんと減らすことができるわけです。
上記の主成分分析の結果を解釈してみましょう。第一主成分のベクトルの成分を見てみると、「英語の点数が高い人は、数学と理科の点数が低い」もしくは同じことですが「英語の点数が低い人は、数学と理科の点数が高い」ということがわかります。俗っぽい言葉で言えば、この第一主成分は理系度もしくは文系度と呼ぶことができるでしょう(固有ベクトルには向き・符号の任意性があるので、それによって呼び名を適当に変えましょう)。この第一主成分のスコア(個々人がこの軸のどこに位置しているか)は、例えば、理系・文系の選択に悩んでいる生徒にアドバイスする際の材料として使うことができるかもしれません。
上記の例は元々の次元が3つしかないし、得られた結果も二次元の散布図を見た時点で想像できることなので、あまり面白くないという人もいるでしょう。もっと面白い応用例を引用します。固有顔というものです。

(左上が平均的な顔。そこから順に第1、第2、第3……と主成分(固有顔)を並べている)
出典:Algorithms and VLSI architectures for low-power mobile face verification by Jean-Luc Nagel
やっていることは簡単で、大量の顔写真に対して主成分分析を行うだけです。ここから得られた主成分(固有ベクトル)は固有顔と呼ばれます。上で引用した図では、320x256ピクセルの画像ファイル200枚に対して主成分分析を行っています(81920次元、N=200)。平均顔(左上)を見ると、男性とも女性ともつかない中性的な顔をしています。そこから順に並ぶ固有顔を見ると、「ヒゲ」「鼻の穴」「眉毛」「眼鏡」などの常識的な顔の特徴をうまく抽出できているのがわかります。このように固有顔は単純な手法でありながら効果的であるため、機械による顔認識技術として実際に使われているそうです。
最後に、主成分分析から派生した特徴抽出の手法を紹介しましょう。パッと思いつくだけでも、回帰を目的とする部分最小二乗(PLS)、単純な直交性ではなく統計的独立性を使う独立成分分析(ICA)、ニューラルネットワークを使う**自己符号化器(オートエンコーダー)**などが挙げられます。ここでは解説をしませんが、どれも主成分分析の原理をわかっていれば基本的なアイデアを理解することは難しくないでしょう。逆に言えば、主成分分析は統計解析の基本なので、理論面を理解したい人はしっかり押さえておくべき手法だと思います。