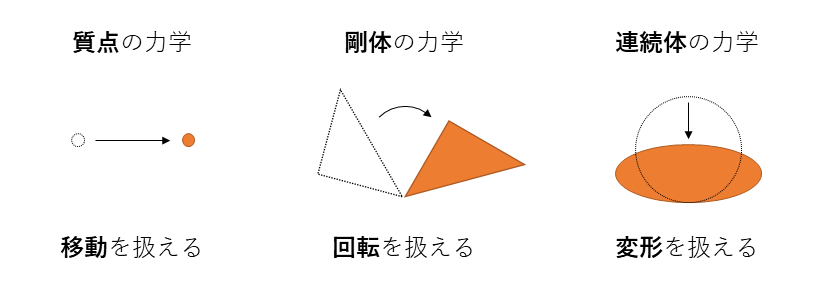
力学というのは、物体の運動を扱う学問です。高校物理で最初に習う力学は、質点を対象としていました。質点の力学は、運動の種類としては移動が扱えますが、質点は**「大きさを持たない」物体であるため、回転運動は扱えません。そこで次に登場したのが、剛体の力学でした。剛体は大きさと形を持っているため、移動に加えて回転も扱えます。しかし剛体は「決して変形しない」という理想化された物体なので、「棒がたわむ」や「ボールがへこむ」といった身近な現象を扱うことができません。そこで、より一般的な物体、つまり「変形する物体」を扱えるようにした力学が、連続体力学です。
「変形」という現象は日常的なので簡単に思えるかもしれませんが、ちゃんと定式化しようとすると割とめんどくさい話になります。以下ではわかりやすさを優先して、大雑把にあらましだけを解説します。
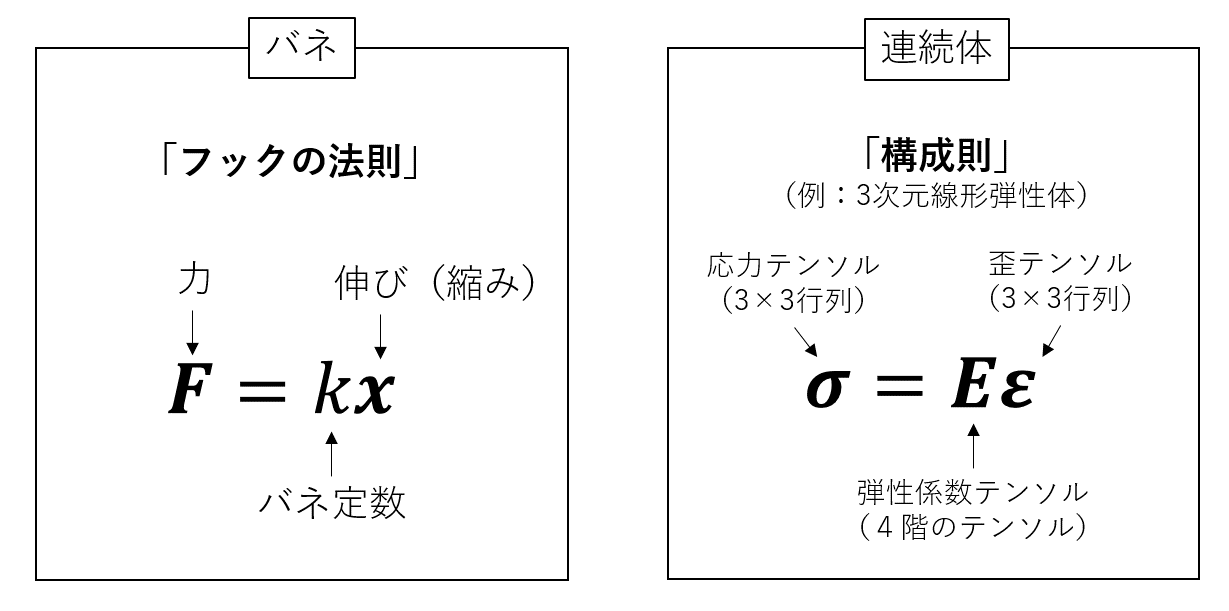
まず、「連続体」という概念を説明します。これは要は、物体は「無数の小さなバネ」で構成されていると思っちゃおう、という話です。バネとは、変形(伸び・縮み)に対して抵抗力を生む物体です。バネにおける変形と抵抗力の関係はフックの法則**(変形∝抵抗力)に従っているのでした。ニュートンの運動方程式(力→変形)とフックの法則(変形→力)の組み合わせによって、バネの運動は完全に記述できます。この考えの延長上として、連続体力学では、「物体の中の小さなバネ達が少しづつ動くことで、全体としての大きな変形を生み出す」と考えるのです。
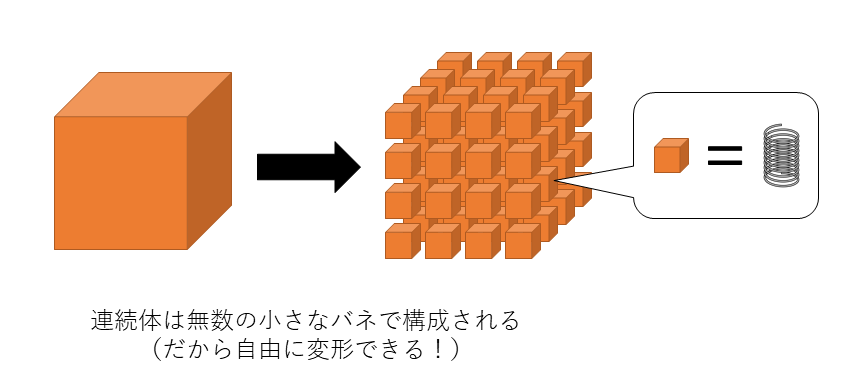
もちろん、バネと連続体では異なる点もあります。ここでは大きく分けて2点、違いを説明します。
まず、バネでは一次元の変形しか扱っていなかったのが、連続体では二次元や三次元の変形も扱うようになるという点です。上から押したボールが横に広がるように、ある方向にかけた力が、異なる方向の変形を生むこともあります。こうした多次元的な変形を記述するためには、ベクトルであった「力」と「変形」は、行列(正確には二階のテンソル※1)である**「応力テンソル」と「歪(ひずみ)テンソル」**という概念に拡張されなければいけません。一口に応力・歪といても定義は色々あるのですが、ここでは一番簡単なバージョン(コーシー応力と微小ひずみ)の2次元空間の場合を示しておきます。
※1 テンソルとは座標系に依存しない多重線形写像のことで、ひとつの座標系で2階テンソルを表現しようとすると行列になります。座標系が変わってもテンソルは変わりませんが、行列の表現は変わります。連続体力学では2階よりも大きいテンソル、後に出るような4階の弾性係数テンソルも出てきます。n階のテンソルはn次元配列で表現することができ、行列が行方向と列方向の2次元的な広がりを持つ数字の羅列であるのと同様、n次元配列は数字の羅列がn次元的な広がりを持っていると考えればよいです。
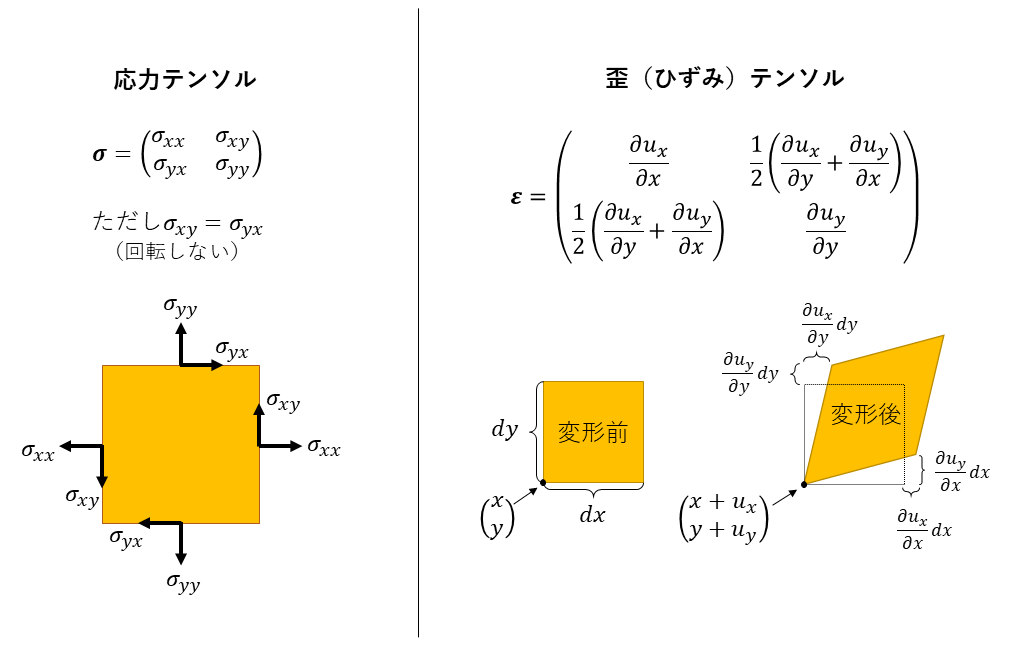
応力テンソル・歪テンソルは、注目したい切断面(の向きを表すベクトル)を与えることで、その切断面に対して**「今どのような力・変形がかかっているか」を(ベクトルとして)教えてくれる関数です。このように力と変形を多次元的に定義しておくことで、バネのような「伸び・縮み」以外の複雑な変形の力学を表現できるようになります。なお、テンソルという言葉には座標変換に対して不変という大事な意味があるのですが、よくわからない人は「我々の持っている常識に合うよう定義されている」程度に思っておきましょう。
もう一つ連続体がバネと異なる点として、変形と抵抗力の関係を「構成則」と呼び、材料の性質ごとに変わっていく点が挙げられます。フックの法則が変形と抵抗力の関係であるように、構成則は応力テンソルと歪テンソルの関係式として記述されます。バネのような構成則(フックの法則)を持つ連続体は線形弾性体と呼ばれますが、バネとは似ても似通わない構成則を考えても構いません。例えば極端な話、水のような流体も連続体に分類され、その構成則を式として書き下すことができます(流体の場合は速度が重要になってくるので、上で示したものとは違う応力・歪の定義を使います)。
構成則は材料の性質を表すものなので、同じ材質の連続体の中では共通します。一方で、応力テンソルや歪テンソルは連続体の中に無数に分布する各点の状態を表す量なので、連続体の中で値はバラバラです。へこんだボールを考えてみてください。へこんでいる部分は応力も歪も大きいですが、へこんでいない部分は応力も歪も小さいはずです。
さて、今簡単に「応力/歪が大きい」などと言いましたが、応力や歪は行列として定義したはずです。複数の値を持つ行列に対して「大きい/小さい」とは、一体何の値に基づいて言うことができるのでしょうか? もう少し問題を詳しく述べましょう。上で述べたように、応力テンソル・歪テンソルは、注目したい切断面を与えることで、その切断面に対して「どのような力・変形がかかっているか」を吐き出す関数です。だから、どの切断面を考えるかによって力や変形の大きさと向きは変わってしまう。となると一意に値を決められない。これが問題なわけです。
ここで役に立つのが、固有値の概念です。応力テンソルの固有値は主応力**、歪テンソルの固有値は主歪と呼ばれます。また、それぞれの固有値に対応する固有ベクトルは主方向と呼ばれます。応力テンソルも歪テンソルも対称行列で表されます(※2)。対称行列は与えられたベクトルを自分の固有ベクトルに射影して足し合わせるように働きます。だから、任意の切断面のベクトルは、応力テンソル・歪テンソルが持つ主方向(二次元の場合は二つの主方向、三次元の場合は三つの主方向)に分解、射影されます。そうすると簡単な計算から、あらゆる向きの中で最大の力あるいは変形(正確には、それらのベクトルのノルム)を与えるのは、最大固有値に対応する固有ベクトル(最大主応力の主方向あるいは最大主歪の主方向)ということがわかります。
例えば、連続体の内部でどのように力や変形が分布しているかを見たいときは、各点で応力テンソルや歪テンソルの最大固有値(最大主応力と最大主歪)を求めればよいわけです(なぜならその点において、その向きより大きい力や変形を与える向きはないのですから)。これらの力や変形の向きに着目したい場合は、固有ベクトル(主方向)の方を調べればよいわけですね。主応力や主歪の値は、物体が破壊される条件に深く関わってくるので、建築や機械の設計においてよく計算されます。建造物や機械に囲まれて生きる現代人ならば、たとえ固有値の出し方を知らなくても、既に固有値問題の恩恵を受けていると言えるかもしれません。
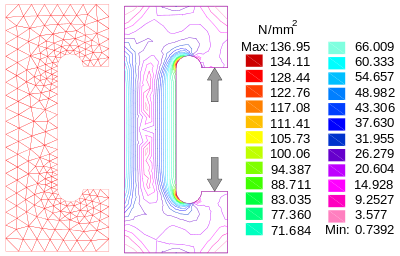
出典:Wikipedia「応力集中」
※2 応力テンソルは連続体にかかるモーメントが表面に渡る積分だけで書かれるという要請から対称行列に、歪テンソルは変位勾配から回転部分を差っ引いたものであるという定義から対称行列になります。なお、以上はコーシー応力の話で、対称じゃない応力テンソルも存在します。