時間的に変化するシステムのことを数学では**「力学系」と呼びます。名前の通り物理学の「力学」から発展した分野ですが、力学が「粒子」や「惑星」といった「物理的実体の運動」を扱っていたのに対し、力学系では「神経細胞の発火」「感染症の広がり」「漁獲高の変動」といった、より抽象的な現象も扱います。とにかく時間変化していれば何でも力学系です。力学系を数式で表現する方法は色々あるのですが、最も一般的なのは常微分方程式(ODE)によるモデル化**です。そのため、以下では力学系=常微分方程式といった体で話を進めていきます。
力学系において、固有値・固有ベクトルは平衡点の安定性という概念に深く関わってきます。安定性は制御工学でも使われる重要な概念です(※1)。ありがたいことに、固有値・固有ベクトルを使うことで、微分方程式を解くことなく力学系の安定性について予言ができます。安定性がわかると何が嬉しいかと言うと、たとえば生態系における個体群動態のモデルならば「複数の種が共存できるか絶滅するか」といった将来の運命について予測することができます(この記事の最後には実際にこの問題を解きます)。
※1 ここでいう安定性とは線形安定性(局所安定性)のことで、基本的には伝達関数の極と同じ概念です。制御系とは要するに外部入力が備わった力学系なので、制御工学には力学系のテクニックがめちゃくちゃ応用されています。
まずは手始めに、次の単純な(しかしながら多くの重要な示唆を含んでいる)力学系について考えてみましょう:
$$ \frac{dx}{dt} = rx $$
この微分方程式は、「ある量 $x$ の変化率は、現在の $x$ の量に比例する」ということを意味しています。$r>0$のとき、この力学系は「生物の個体数の増加」のモデルとして解釈できます($x$ は個体数)。$r<0$のとき、 この力学系は「放射性元素の崩壊」のモデルとして解釈できます($x$ は放射性元素の量)。
初歩的な微積の知識があれば、この微分方程式の解は$ x = x(0) e^{rt} $という指数関数になることがわかります($x(0)$は初期値)。すなわち、$r>0$のときは指数的に増え続け、$r<0$のときは指数的に減り続けます:
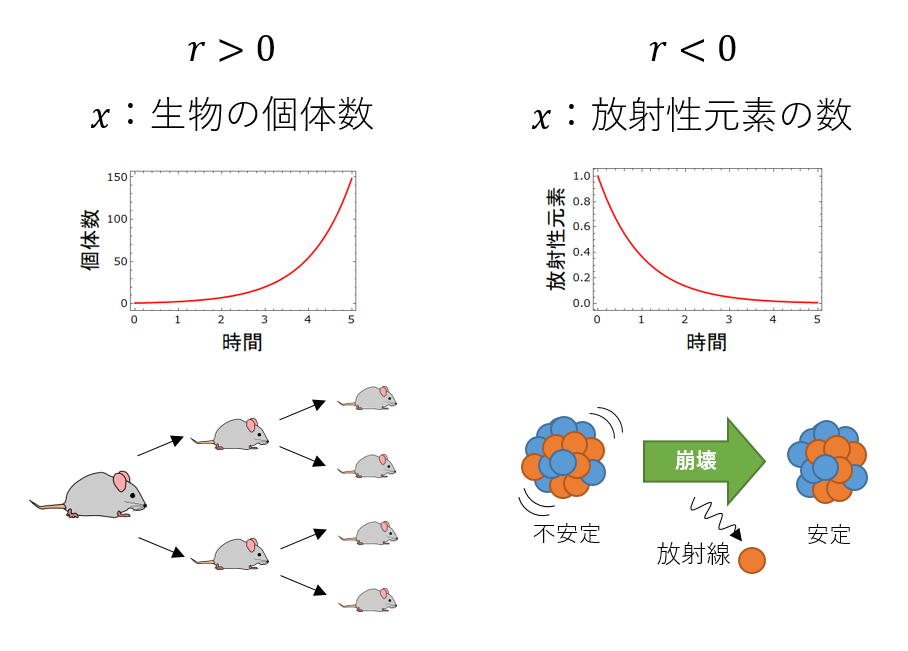
ただし例外として、初期値が原点$x=0$にある場合、つまり $x(0)=0$ の場合、 恒久的に$x(t)=0$ となり、$r$の値によらず力学系の状態は時間的に変化しません。このような点を平衡点と呼びます(※2)。一般の力学系に関して言えば、すべての変数の変化率(微分方程式の右辺)が0になるような点を平衡点と呼びます。
(※2)固定点や不動点とも呼ばれます
平衡点という概念を用いると、上述した力学系の解について、別の見方をすることができます:「平衡点$x=0$以外からスタートした解軌道は、$r>0$のときは平衡点から離れていき、$r<0$のときは平衡点に近付いていく」。$r \ne 0$ならば、初期値が平衡点からほんの少しでもズレていたなら、平衡点から離れるか、平衡点に近づくかのどちらかしかありえません。つまり、$r$は平衡点の安定性を決めるパラメータであると言えます($r>0$なら平衡点は不安定、$r>0$なら平衡点は安定)。
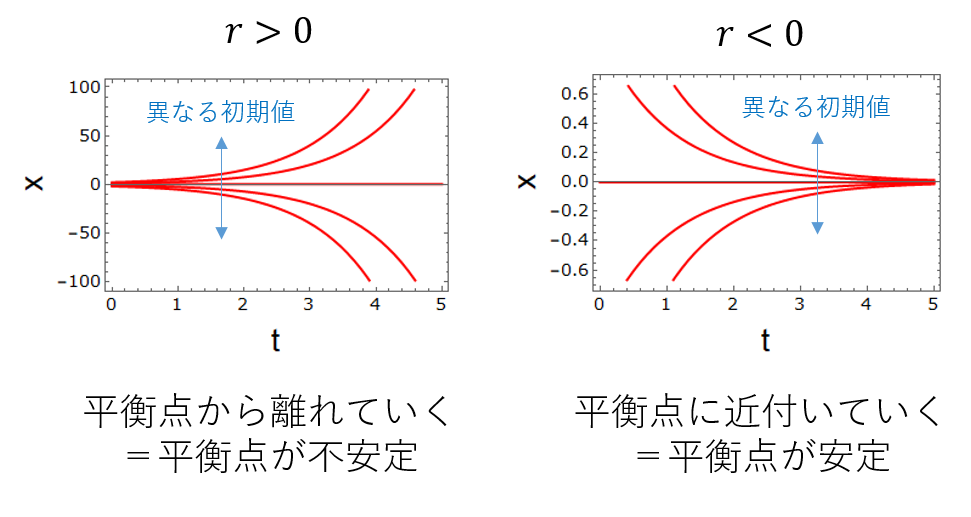
次に、もう少し複雑なモデル、指数増殖モデルを少し改変したモデルを使って平衡点や安定性を調べてみましょう:
$$ \frac{dx}{dt} = rx \left( 1-\frac{x}{K} \right) $$
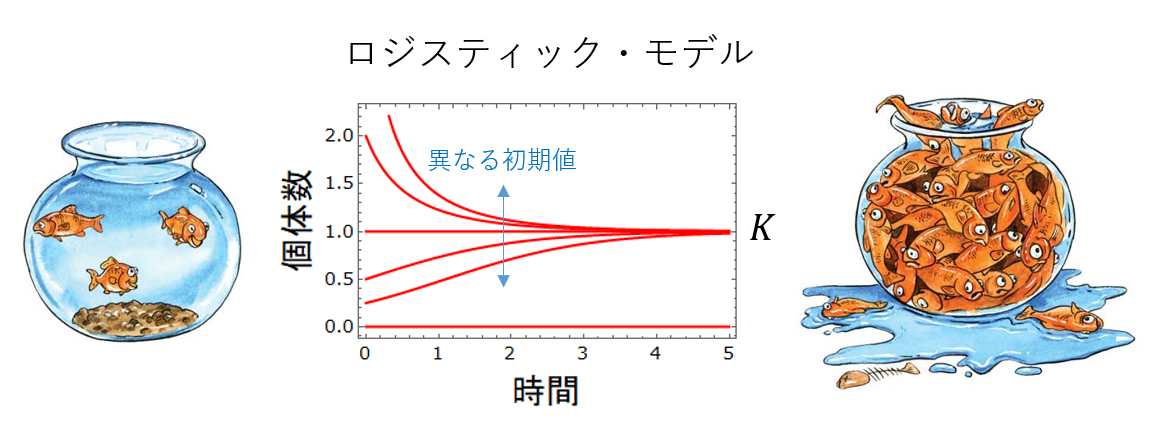
この微分方程式はロジスティック方程式と呼ばれ、個体の増殖に上限がある場合のモデルとして使われます(増殖を考えるので$r>0$とします)。環境収容力と呼ばれるパラメータ$K>0$が個体数の上限を決めています。明らかに、$x=K$は平衡点です。指数増殖のときにあった$x=0$も依然として平衡点として残っています。ダイナミクスとしても、$x$が$K$に比べて小さいときは後ろの$(1-x/K)$が無視できるので、先の指数増殖モデルと同じような振る舞いをします。しかし、今度は線形($x$の一次式)ではない非線形の微分方程式なので、先程と同じ様には解けません。とはいえ、ちょっと工夫すれば簡単に解くことができて、その解はロジスティック関数という、機械学習でよく使われる形の関数になります(式は重要でないので載せません):
出典:http://www.ecobrasil.eco.br/
上図に示したいろいろな初期値から始めた解軌道を見れば、$ x=0 $は不安定な平衡点で、$ x=K $は安定な平衡点であると推測できるでしょう。しかし以下では、実際に微分方程式を解くことなく(あるいは解けない場合でも)、平衡点の安定性を求められる手法があることをご紹介します。
まず、適当な平衡点$ x^* $のまわりにだけ注目して、$ \Delta x=x-x^* $と変数変換しましょう。$ \Delta x $は平衡点からのズレを現しています。いま、平衡点からのズレが十分に小さいと考えて、微分方程式の右辺(簡単のため$ f(x) $と置く)をテイラー展開して、1次の項で打ち切ります(こうした作業を線形化と呼びます):
\frac{dx}{dt}=f(x)\\
=f(x^*+\Delta x)\\
\approx f(x^*)+\frac{df}{dx}(x^*)\Delta x
$ x^* $が定数であること、かつ平衡点であるという条件$ f(x^*)=0 $から、平衡点からのズレ$ \Delta x $に関して、次の微分方程式が成り立ちます。
$$ \frac{d}{dt} \Delta x=\frac{df}{dx}(x^*)\Delta x $$
この式は指数増殖モデルと同じ形をしています。このことから、指数増殖モデルの $ r $ と同じように、微分係数 $df/dx$ の符号だけで、平衡点$x^*$の安定性が決まることがわかります。実際にロジスティック方程式について平衡点まわりでの微分係数を計算してみましょう:
\frac{d}{dx} \left[ rx \left( 1-\frac{x}{K} \right) \right] =r \left( 1-2\frac{x}{K} \right) \\
=\left\{
\begin{array}{l}
r\;\;\;\;\;\;\;(x=0)\\
-r\;\;\;\;(x=K) \end{array}
\right.
$ r>0 $ と仮定していたことを思い出せば、$x=0$は不安定、$x=K$は安定ということになります。この結果は解軌道の図から見て取れる安定性と一致しています!
これで、非線形の力学系についても平衡点の安定性を求める方法がわかりました。ここまでの話は、あくまでも一次元力学系(変数が一個しかない力学系)の話です。多次元、つまり変数が複数個ある場合の力学系については、どのようにして安定性を求めるのでしょうか? まずは多次元で線形の場合についてお話しましょう。ここでは、よく物理(力学)で使われる例を出します:
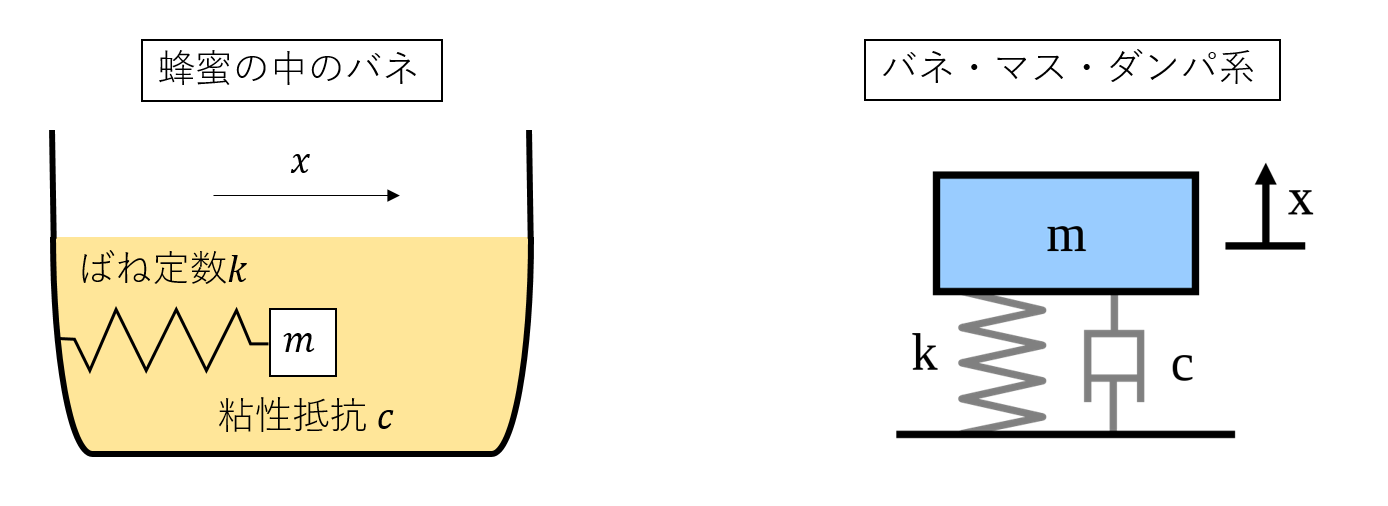
\left\{
\begin{array}{l}
\displaystyle \frac{dx}{dt} = v\\
\displaystyle m \frac{dv}{dt} = -kx - cv \end{array}
\right.
これは、蜂蜜のような粘っこい液体中のバネに繋がれた質点(重り)の運動方程式になっています(いわゆるバネ・マス・ダンパ系と同じですが、ダンパって何?という人もいると思うので……)。重りにかかっている力は2つで、バネの弾性力$kx$(フックの法則)と、液体から受ける粘性抵抗力$cv$(ストークスの法則)です。この力学系の状態変数は重りの位置$x$と、重りの速度$v$の2つですから、多次元の力学系になっています。また、右辺はすべて状態変数の1次で書かれているので、線形の力学系です。多次元の線形力学系は、行列とベクトルを使って、簡潔に書き直すことができます:
\frac{d}{dt} \left( \begin{array}{cc} x\\ v\\ \end{array} \right) =
\left(\begin{array}{cc} 0 & 1 \\ -k/m & -c/m \\ \end{array} \right)
\left( \begin{array}{cc} x\\ v\\ \end{array} \right)
\\
\frac{d\boldsymbol{x}}{dt} = A\boldsymbol{x}
\\
{\rm where} \; \boldsymbol{x}=\left( \begin{array}{cc} x\\ v\\ \end{array} \right),\;A=\left(\begin{array}{cc} 0 & 1 \\ -k/m & -c/m \\ \end{array} \right)
状態変数(位置と速度)をまとめて、 $\boldsymbol{x}$ というベクトルにしました。$A$は状態変数間の相互作用を記述している行列で、制御工学だと状態行列と呼ばれています。指数増殖モデルと似ている形になりました。指数増殖モデルと同様、多次元になっても線形力学系の平衡点は原点 $\boldsymbol{x}=\boldsymbol{0}$ だけです。安定性についてはどうでしょうか? 指数増殖モデルでは、スカラーである$r$の符号によって安定性を決定できたのでした。しかし、$A$はスカラーではなく行列ですので、同じ方法は使えません。そこで一工夫を加えます。$A$の固有ベクトルを並べた行列$P$を使って、状態変数を $\boldsymbol{y}:=P^{-1} \boldsymbol{x}$ と線形変換します:
\frac{d\boldsymbol{x}}{dt} = A\boldsymbol{x}\\
P^{-1} \frac{d}{dt} \boldsymbol{x} = P^{-1}A(P P^{-1})\boldsymbol{x} \\
\frac{d}{dt} P^{-1} \boldsymbol{x} = (P^{-1}A P) (P^{-1}\boldsymbol{x}) \\
\frac{d\boldsymbol{y}}{dt}= D\boldsymbol{y}
$A$を固有値が対角に並んだ行列 $D:=P^{-1}A P$ に書き直すことができました(*2)。
(*2) 厳密に言えば、行列を対角化できるのは固有値がすべて実数で相異なる場合だけです。しかし、固有値が複素数の場合は実標準形で、固有値に重複がある場合はジョルダン標準形でブロック対角化ができます。
非対角成分がゼロなので、$ \boldsymbol{y}=(y_1,y_2)^T $を構成する$y_1$と$y_2$は独立に解けます:
\frac{d}{dt} \left( \begin{array}{cc} y_1\\ y_2\\ \end{array} \right) =
\left(\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \\ \end{array} \right)
\left( \begin{array}{cc} y_1\\ y_2\\ \end{array} \right)\\
\left\{
\begin{array}{l}
y_1 = y_1(0) e^{\lambda_1 t}\\
y_2 = y_2(0) e^{\lambda_2 t} \end{array}
\right.
ここで、$\lambda_1$ と $\lambda_2$ は $ A $ の固有値です。さらに、$\boldsymbol{y}$ は $\boldsymbol{x}$ の線形変換なので、答えは次の形になることがわかります:
\left\{
\begin{array}{l}
x(t) = C_1 e^{\lambda_1 t} + C_2 e^{\lambda_2 t}\\
v(t) = C_3 e^{\lambda_1 t} + C_4 e^{\lambda_2 t} \end{array}
\right.
$C_1~C_4$は初期値と固有ベクトルに依存した定数です。平衡点(原点)が安定であるということは、$t\rightarrow\infty$のときに $x,v\rightarrow 0$ になるということです。よって、平衡点が安定であるためには、「状態行列 $A$ の固有値がすべて負であること(※3)」が必要になることがわかります。
(※3) 正確には、固有値は一般的に複素数になりうるので、固有値の「実部」が負になることが安定性の条件です。固有値に虚部があると、解が振動するようになりますが、安定性についての議論には影響を与えません(振動する理由は、オイラーの公式からわかります)。
実際に行列 $A$ の固有値を求めると、
$$ \frac{-c \pm \sqrt{c^{2} - 4km} }{2m} $$
となるので、$ c>0 $である限り、平衡点は安定であることがわかります。つまり、粘性抵抗がある限り、最終的に運動は必ず止まる、ということです。
最後に、非線形かつ多次元の力学系で安定性を求める方法をご紹介しましょう。最初の述べたように、複数の種の生物が存在する生態系のモデルを扱います:
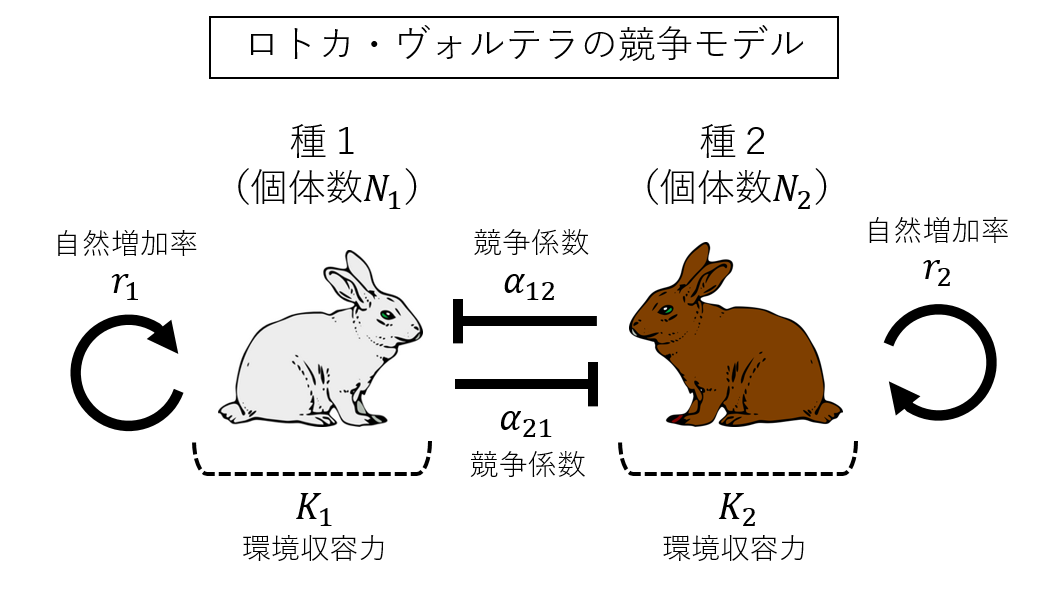
\left\{
\begin{array}{l}
\displaystyle \frac{dN_1}{dt} = r_1 N_1 \left( 1-\frac{N_1+\alpha_{12} N_2}{K_1} \right) \\
\displaystyle \frac{dN_2}{dt} = r_2 N_2 \left( 1-\frac{N_2+\alpha_{21} N_1}{K_2} \right) \end{array}
\right.
これはロトカ・ヴォルテラの競争モデルといって、食料などの資源を巡って競争する2種の生物の個体数変化を記述したモデルになっています。式を見ればわかるように、ロジスティックモデルがベースにあります。ロジスティック方程式をそれぞれの種について立て、そこに競争の影響を加えた形になっています。ロジスティックモデルに存在しなかった追加されたパラメータ$\alpha_{12}>0$と$\alpha_{21}>0$が、それぞれ「種2が種1に与える影響の強さ」と「種1が種2に与える影響の強さ」です。
まずはこの力学系の平衡点を探しましょう。右辺をすべてゼロになる代数方程式を解けば、
\left( \begin{array}{cc} N_1 \\ N_2\\ \end{array} \right)=
\left( \begin{array}{cc} 0 \\ 0\\ \end{array} \right),
\left( \begin{array}{cc} K_1 \\ 0\\ \end{array} \right),
\left( \begin{array}{cc} 0 \\ K_2\\ \end{array} \right),
\left( \begin{array}{cc}
\displaystyle \frac{K_1 - \alpha_{12} K_2}{1-\alpha_{12} \alpha_{21}} \\
\displaystyle \frac{K_1 - \alpha_{12} K_2}{1-\alpha_{12} \alpha_{21}}\\ \end{array} \right)
の4つが解として得られます。興味深いのは4つ目の解で、これはどちらの種の個体数もゼロではない平衡点の存在、つまり2種の生物が競争しているにもかかわらず共存できる可能性を意味しています。しかし、平衡点が存在するといっても、その平衡点が安定でなければ、現実的にたどり着くことはできません。なので、この4つ目の平衡点の安定性について調べましょう。
非線形多次元の力学系に対して、どのようにして平衡点の安定性を求めればよいのでしょうか? 実は、既にここまでに記した手法を応用するだけでできます。非線形の力学系では右辺を線形化しました。多次元の力学系では行列の固有値を求めました。ということは、非線形で多次元の力学系では、右辺を線形化して行列の形に書き直し、その固有値を求めればよいのです。多次元の線形化では、すべての状態変数の右辺を、すべての状態変数で微分する必要があります(多変数のテイラー展開)。そうすると、線形力学系と同じように、右辺を行列とベクトルの掛け算に書き直すことができます。こうして得られた行列をヤコビ行列と呼びます。ヤコビ行列は微分係数の多次元版です。ヤコビ行列の固有値の実部がすべて負なら、その平衡点は安定であると言えます。
いま、共存解を $ (N_{1}^* , N_{2}^*) $と置くと、その周りでのヤコビ行列 $J$ は次のように書けます:
J=\left(\begin{array}{cc} \displaystyle -\frac{r_1 N_1^*}{K_1} & \displaystyle -\frac{\alpha_{12} r_1 N_1^*}{K_1} \\
\displaystyle -\frac{\alpha_{21} r_2 N_2^*}{K_2} & \displaystyle -\frac{r_2 N_2^*}{K_2} \\ \end{array} \right)
そして、この行列の固有方程式は、次のようなものになります:
\lambda ^2 + \left( \frac{r_1 N^*_1}{K_1}+\frac{r_2 N^*_2}{K_2} \right) \lambda
+ (1-\alpha_{12} \alpha_{21})\frac{r_1 r_2 N^*_1 N^*_2}{K_1 K_2} =0
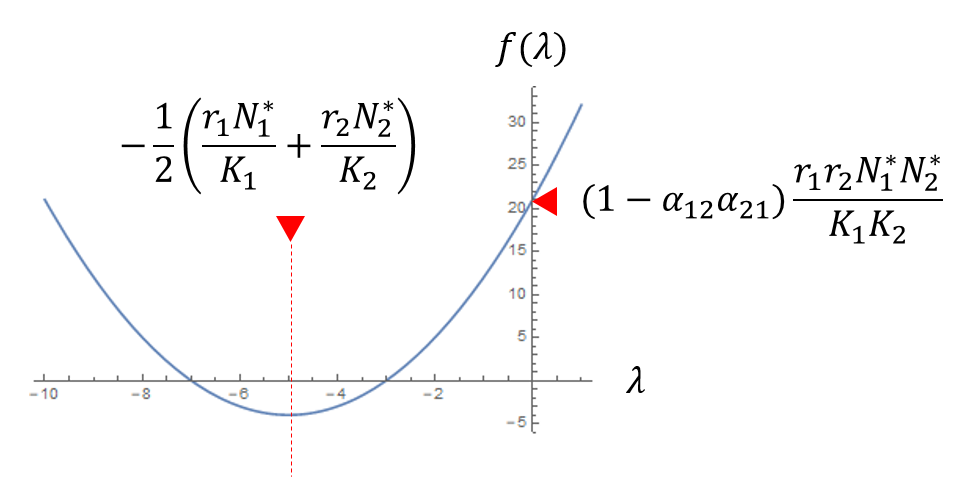
すべてのパラメータが正で、共存解も正でなければならないことを考えれば、この方程式の解は相異なる2つの実数になることがわかります。また、固有方程式の左辺 $f(\lambda)$ をグラフにしてみると:
という形になるため、2つの実解が負であるためには、$\alpha_{12} \alpha_{21}<1$でなければなならないことわかります。$\alpha_{12}$ と $\alpha_{21}$ は競争の強さを表すパラメータでした。結局、2種が共存するためには、競争の影響が小さくなくてはならない、ということです。
このようにヤコビ行列の固有値によって平衡点の安定性を求める方法を、線形安定性解析や局所安定性解析と呼びます。非線形多次元力学系は非常に多くの複雑な現象をモデル化できますが、それが必ず微分方程式として解けるとは限りません。一方、線形安定性解析は平衡点とヤコビ行列さえ求まれば行えますので、力学系の解析においてとても重宝がられます。