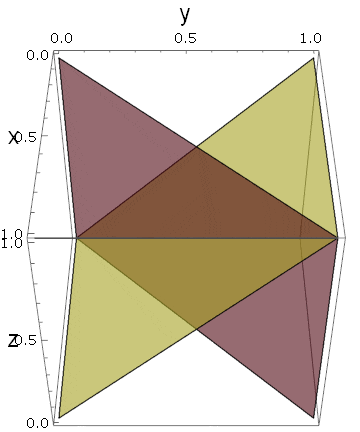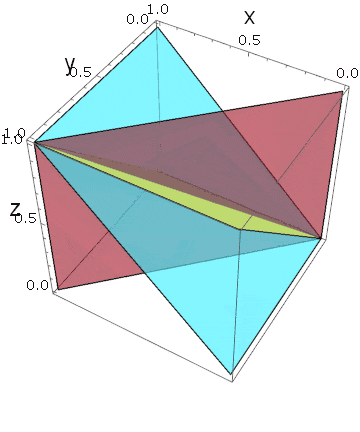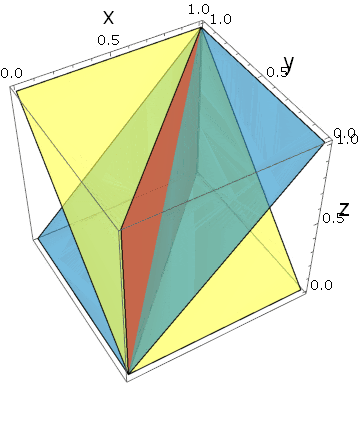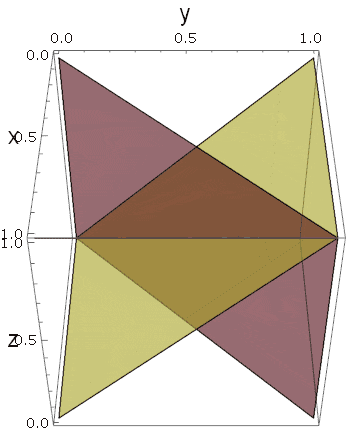ガンマ関数の形が謎すぎ問題
$${\Gamma (k)}$$
こちらの記号、統計学や確率論を勉強していると一度は目にしたことはあるかと思います。
そう、ガンマ関数です。
例えばχ二乗検定、t検定、分散分析といった統計検定手法はよく使われるかと思いますが、それぞれ内部で使われている確率分布であるχ二乗分布、t分布、F分布の定義中にはガンマ関数が含まれています。
さらに名前が示す通り、ガンマ分布という確率分布の中にもガンマ関数が現れます。
ガンマ関数の性質自体は覚えやすいもので、階乗
$$k!=k \cdot (k-1) \cdot (k-2) \cdots 3 \cdot 2 \cdot 1$$
の定義域を自然数以外の実数(あるいは複素数)に一般化した関数であるということは、皆さんよくご存知のことかと思います。
つまり、引数は一つずれますが、
$${\Gamma (k+1)} = k!$$
ということですね。
しかし、その一方で、ガンマ関数の定義式
$${\Gamma (k)} = \int_{0}^{\infty}t^{k-1}e^{-t}dt$$
については、形をすぐ思い出せる人は少ないのではないでしょうか?
突然テロリストに 「何も見ずにガンマ関数を書き出せ」 と命じられて、生き延びる自信はありますか?
私は、肩のマイナス1を忘れたりして、銃殺される気がします。
「冪関数と指数関数との掛け算を積分すると、階乗になる」 という事実は、かなり直感に反しますよね。
多くの教科書では、「トップダウンにガンマ関数の形を与える⇒部分積分を使ってガンマ関数が階乗の性質を持つことを証明する」以上の説明はない気がします。
では歴史上、最初にガンマ関数を考案したオイラーはどうやってガンマ関数を作ったかというと、無限乗積の形で導入したとのことで、いまよく知られている形とはちょっと違います。
どちらの方法にしろ、現在よく知られるガンマ関数が、何故あんな形になったのかについて、納得する答えを提供してくれません。
そこで今回は、シンプルな確率モデルであるポアソン過程を起点として、ボトムアップに「ガンマ関数が階乗の一般化であること」=「冪関数と指数関数との掛け算を積分すると階乗になること」を示していこうかと思います。
具体的には、レアイベントの待ち時間の分布である指数分布から、レアイベントk回分の待ち時間であるアーラン分布を導出し、アーラン分布を積分することでガンマ関数の式を出します。
アーラン分布はあまり聞き慣れないかもしれませんが、基本的にはガンマ分布と同じです。ガンマ分布の形状パラメータ$k$を自然数に限定したものがアーラン分布になります。アーラン分布をポアソン分布から導出する方法もありますが、今回は指数分布から導出します(前者の方が簡単かもしれませんが、たぶん後者の方が面白いです)。
1. ポアソン過程とは
ポアソン過程とは、過去に依存せず、常に一定確率で起きるランダムなレアイベントのことです。よく例に挙がるのが、 「お店に客が来る」「電話がかかってくる」「地震が起こる」 などです。つまり、めちゃくちゃ簡単な確率過程で、いろいろな場面で使われるシロモノです。
ポアソン過程を特徴づけるパラメータはただひとつ、単位時間あたりの平均生起回数$\lambda$です。
$\lambda$を持つポアソン過程は、どの時点$t$においても、十分に小さい時間区間$\Delta t$あたりにそのイベントが起こる確率が$\lambda \Delta t$ということになります。
2. ポアソン過程から指数分布を導く
ポアソン過程に付随する確率分布が2つあります。
ひとつは、ポアソン過程に従うイベントの 「生起回数」 の確率分布で、こちらはポアソン分布になります。今回は使わないので説明を省略します。
もうひとつは、ポアソン過程に従うイベントの 「待ち時間」 の確率分布で、こちらが指数分布になります。「待ち時間」とは、「ある時点から、イベントが初めて起こるまでの時間」のことを指します。
指数分布を導出してみましょう。
今、待ち時間の確率密度関数を$p(t)$とします。
時点$t$でイベントが初めて起こるということは、「$t$までイベントが起きないで、次の微小時間区間$\Delta t$に初めてイベントが起こる」ということです。これを数式で書くと、
$$
p(t)\Delta t = \left( 1-\int_{0}^{t} p(t) dt \right) \cdot \lambda \Delta t
$$
となります。両辺の$\Delta t$を打ち消し合い、$t$で微分すると、
$$
\frac{d}{dt}p(t) = 1- \lambda p(t)
$$
という微分方程式が得られます。これを積分して、確率密度関数の規格化条件$\int _{0}^{\infty} p(t)dt = 1 $によって積分定数を定めれば、
$$
p(t) = \lambda e^{-\lambda t}
$$
と、確率密度関数が陽な形で得られます。指数関数を含んでいるため、指数分布と呼ばれるわけですね。
今後は$p(t)$という記号を他の確率分布にも使いたいため、指数分布の確率密度関数を次のように書くことにしましょう。
$$
{\rm Exponential}(t;\lambda) = \lambda e^{-\lambda t}
$$
ちなみに、指数分布の期待値は部分積分を使って計算できて、
$$
E[t]=\int _{0}^{\infty} t \cdot {\rm Exponential}(t;\lambda)dt = \frac{1}{\lambda}
$$
となります。 「平均生起回数の逆数は平均待ち時間」 というのは、ポアソン過程のわかりやすい特徴です。注目する現象によっては、$\lambda$ではなく、$\mu=1/\lambda$とか置いて平均待ち時間の方をパラメータに取ることもあります(半減期とか)。
3. 指数分布からアーラン分布を導く
指数分布はレアイベントが一回起こるまでの待ち時間でした。では、レアイベントが$k$回起こるまでの待ち時間を考えてみましょう。期待値は$k/ \lambda $になることが想像つくかと思いますが、確率密度関数を導出するのは少し面倒です。
「$k$個の指数分布の実現値${t_1,t_2,\cdots t_k}$の合計が偶然$t$になる確率」を考える必要があります。ある関係式$y=f(\boldsymbol{x})$を使って確率変数を$\boldsymbol{x}$から$y$に変換をするために、次のような手順を踏みます:
p(y)=\int p(\boldsymbol{x},y)d\boldsymbol{x}\\
=\int p(y|\boldsymbol{x})p(\boldsymbol{x})d\boldsymbol{x}\\
=\int \delta (y-f(\boldsymbol{x})) p(\boldsymbol{x})d\boldsymbol{x}
つまり、同時確率分布をデルタ関数で畳み込みます。これを指数分布の合計に対してやると、具体的には次のような形になります:
$$
p(t;\lambda,k) = \int_{0}^{\infty} \cdots \int_{0}^{\infty} \delta \left(t-\sum_{i=1}^{k}t_i \right) \prod_{i=1}^{k} {\rm Exponential}(t_i;\lambda) dt_1 \cdots dt_k
$$
まず、$t_k$だけ積分してデルタ関数を消しましょう。
= \int_{0}^{\infty} \cdots \int_{0}^{\infty} \delta \left( t-\sum_{i=1}^{k-1}t_i -t_k \right) {\rm Exponential}(t_k;\lambda)dt_{k} \prod_{i=1}^{k-1} {\rm Exponential}(t_i;\lambda) dt_1 \cdots dt_{k-1} \\
= \int \cdots \int_{D} {\rm Exponential} \left( t-\sum_{i=1}^{k-1}t_i;\lambda \right) \prod_{i=1}^{k-1} {\rm Exponential}(t_i;\lambda) dt_1 \cdots dt_{k-1} \\
= \int \cdots \int_{D} \lambda e^{-\lambda (t-\sum_{i=1}^{k-1}t_i)} \prod_{i=1}^{k-1} \lambda e^{-\lambda t_i} dt_1 \cdots dt_{k-1} \\
最後の行で指数分布の定義を開きました。また、$t_k$を消したことにより、積分領域$D$は各変数が非負であることに加え、
$$t_k \ge 0 \Leftrightarrow \sum_{i=1}^{k-1}t_i \le t $$
という条件も追加されていることに注意です。さらに総乗を開いて、まとめていきます:
= \int \cdots \int_{D} \lambda e^{-\lambda (t-\sum_{i=1}^{k-1}t_i)} \lambda^{k-1} e^{-\lambda (\sum_{i=1}^{k-1}t_i)} dt_1 \cdots dt_{k-1} \\
= \int \cdots \int_{D} \lambda^k e^{-\lambda t} dt_1 \cdots dt_{k-1} \\
= \lambda^k e^{-\lambda t} \int \cdots \int_{D} dt_1 \cdots dt_{k-1} \\
驚いたことに、ごちゃごちゃした部分はすべて積分記号の前に出すことが出来ました。
つまり、あとは 積分領域$D$の体積(測度)$V_D$ を計算するだけです。いまいちど積分領域$D$を明示的に書くと、
D= \left\{ \boldsymbol{t}=(t_1,\cdots,t_{k-1})|\sum_{i=1}^{k-1}t_i \le t, t_1,\cdots,t_{k-1} \ge 0 \right\}
ですが、これは変数変換
x_{k-1}:=t-t_{k-1}\\
x_i:=x_{i+1}-t_{i} ~~ \text{for} ~~ i=1,2,\cdots, k-2
によって、次のような領域に変換できます。
D= \left\{ \boldsymbol{x}=(x_1,\cdots,x_{k-1})|0 \le x_1 \le x_2 \le \cdots \le x_{k-1} \le t \right\}
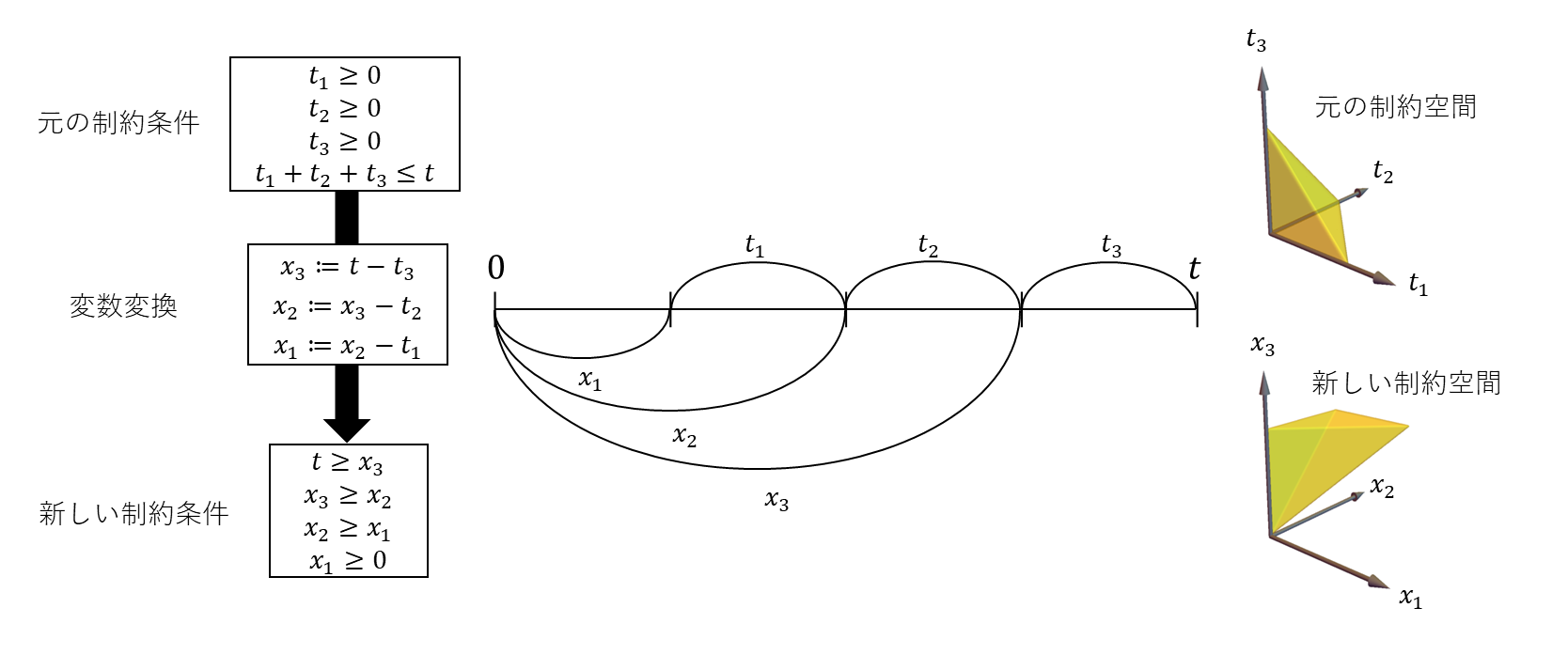
三次元空間で説明すると、下図のような変換です。
これ(右下の物体)は、立方体を$x_1=x_2,~x_2=x_3,~x_3=x_1$という3つの平面で分断したときに作られる断片の一つです。それぞれの平面のどちら側を選ぶかによって、他にも似たような断片が得られます。今回は、$x_1 \le x_2,~x_2 \le x_3,~x_3 \ge x_1$となる側を選んだわけです。
では、$3$個の平面から、何個の断片が得られるでしょうか?
それぞれの平面に対して両側があるので、$2^3$個の断片が得られるような気がしますが、例えば $ x_1 \le x_2,~x_2 \le x_3$ の範囲で $ x_3 \le x_1$ が成り立つ空間は測度ゼロであることに注意しなければなりません。推移的な狭義全順序集合が含まれる場合にのみ、ゼロでない体積が生まれます。つまり、$x_1 < x_2 < x_3 $のように書ける場合です。明らかに、このような順序は、次元数の順列の数だけあります($x_1 < x_3 < x_2 ,x_2 < x_3 < x_1 ,\cdots$):
$${}_3P_3=3!=3 \cdot 2 \cdot 1=6$$
実際に3つの平面を描いてみると、ある角度で立方体が6つに分割されていることがわかります:
しかも、変数の入れ替えに対する対称性から、これら6つの断片は同じ体積を持っていることになります。
同様の議論を$k-1$次元で行えば、体積$V_D$を求めることは簡単にできます。
まず、一辺の長さが$t$である$k-1$次元超立方体の体積は$t^{k-1}$です。
この超立方体は${}_{k-1}C_2$個の超平面によって、$(k-1)!$個の断片に分かれます。
よって、ひとつひとつの断片の大きさは、
$$ V_D= \frac{t^{k-1}}{(k-1)!}$$
となります。これを確率密度関数に戻せば、
p(t;\lambda,k) = \lambda^k e^{-\lambda t} \int \cdots \int_{D} dt_1 \cdots dt_{k-1} \\
= \lambda^k e^{-\lambda t} \frac{t^{k-1}}{(k-1)!}\\
= \frac{\lambda^k}{(k-1)!} t^{k-1} e^{-\lambda t}
となります。最後の変形は、確率変数$t$を右に寄せただけです。
というわけで、アーラン分布の確率密度関数を無事に導出できました。
$${\rm Erlang}(t;\lambda,k) = \frac{\lambda^k}{(k-1)!} t^{k-1} e^{-\lambda t} $$
4. アーラン分布からガンマ関数を導く
ここまで来たら、あと一息です。
先のセクションでは確率密度関数を変数変換しただけなので、導かれた関数は積分すれば1になるよう規格化されているはずです。これを認めるところからスタートします。
\int_0^\infty {\rm Erlang}(t;\lambda,k) dt = 1\\
\int_0^\infty \frac{\lambda^k}{(k-1)!} t^{k-1} e^{-\lambda t} dt = 1\\
\frac{1}{(k-1)!} \int_0^ \infty (\lambda t)^{k-1} e^{-(\lambda t)} d(\lambda t) = 1\\
\frac{1}{(k-1)!} \int_0^ \infty t^{k-1} e^{-t} dt = 1\\
変換の前後で同じ記号を使ってややこしいですが、$\lambda t \rightarrow t$と変数変換をしました。最後に、係数$(k-1)!$を両辺にかけてあげれば、
$$\int_0^ \infty t^{k-1} e^{-t}dt = (k-1)! $$
となります。この左辺はまさに私達がガンマ関数と呼んでいるものであり、確かに「冪関数と指数関数との掛け算を積分すると階乗になること」が導出できました。
ガンマ関数がこのような形になった由来を今回の導出方法から考えてみると、
冪関数⇐超立方体の体積
指数関数⇐指数分布
階乗⇐取りうる順序の数
という説明ができます。
また、$k-1$という半端な数字も、「もともと$k$個の指数分布を考えていたけど、制約条件のために自由度が1つ減った」ということで納得ができます。
これで無人島に流されてもガンマ関数を導出できるし、テロリストにも撃たれずに済みそうですね。
おしまい。