問題
微分のチェーンルールを応用して、2層フィードフォワードネットワークのヘッセ行列の要素について(5.93), (5.94), および(5.95)の結果を導け。
参考
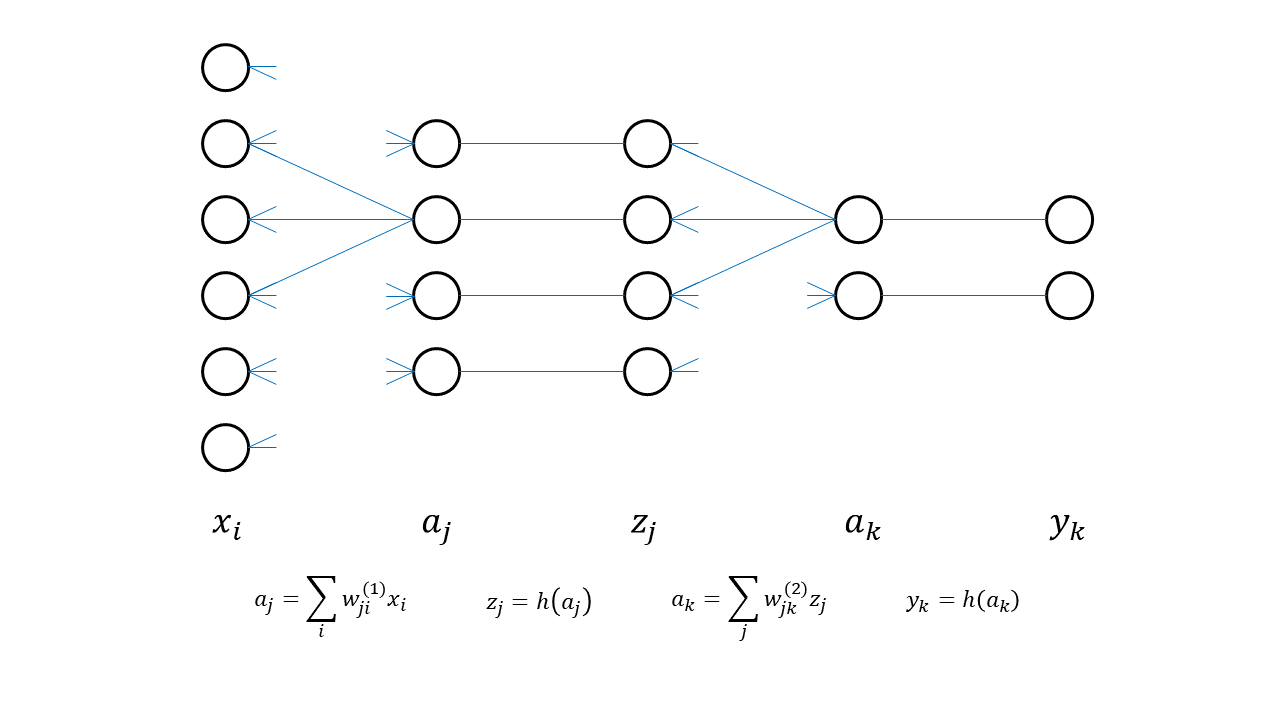
2層フィードフォワードネットワーク
ヘッセ行列
\begin {align*}
\delta_{k}=\frac{\partial E_{n}}{\partial a_{k}}, \quad M_{k k^{\prime}} \equiv \frac{\partial^{2} E_{n}}{\partial a_{k} \partial a_{k^{\prime}}}
\tag{5.92}
\end {align*}
1.両方の重みが第2層にある:
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{k j}^{(2)} \partial w_{k^{\prime} j^{\prime}}^{(2)}}=z_{j} z_{j^{\prime}} M_{k k^{\prime}}
\tag{5.93}
\end {align*}
2.両方の重みが第1層にある:
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{j^{\prime} i^{\prime}}^{(1)}}=x_{i} x_{i^{\prime}} h^{\prime \prime}\left(a_{j^{\prime}}\right) I_{j j^{\prime}} \sum_{k} w_{k j^{\prime}}^{(2)} \delta_{k}\\
\quad+x_{i} x_{i^{\prime}} h^{\prime}\left(a_{j^{\prime}}\right) h^{\prime}\left(a_{j}\right) \sum_{k} \sum_{k^{\prime}} w_{k^{\prime} j^{\prime}}^{(2)} w_{k j}^{(2)} M_{k k^{\prime}}
\tag{5.94}
\end {align*}
3.重みは1つの層に1つずつある:
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{k j^{\prime}}^{(2)}}=x_{i} h^{\prime}\left(a_{j^{\prime}}\right)\left\{\delta_{k} I_{j j^{\prime}}+z_{j^{\prime}} \sum_{k^{\prime}} w_{k^{\prime} j^{\prime}}^{(2)} M_{k k^{\prime}}\right\}
\tag{5.95}
\end {align*}
解答
解答としては問題文の通りに1.2.3.を順に確認していくことになる。ただし、同じ$a$でも添字によって意味合いが異なってしまうため、常に添字に注意しながら微分を行なっていくことになる。
1.両方の重みが第2層にある:
\begin {align*}
a_{j}=\sum_{i} w_{j i} z_{i}
\tag{5.48}
\end {align*}
より、
\begin {align*}
a_{k}=\sum_{j} w_{k j} z_{j}
\tag{5.48'}
\end {align*}
となる。この(5.48')を用いると、
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{k j}^{(2)} \partial w_{k^{\prime} j^{\prime}}^{(2)}} =& \frac{\partial^{2} E_{n}}{\partial a_{k} \partial a_{k^{\prime}}}\frac{\partial a_{k}}{\partial w_{k j}^{(2)}} \frac{\partial a_{k^{\prime}}}{\partial w_{k j}^{(2)}}
\\=& z_{j} z_{j^{\prime}} M_{k k^{\prime}}
\tag{5.93}
\end {align*}
よって(5.93)は示すことができた。
2.両方の重みが第1層にある:
\begin {align*}
\frac{\partial E_{n}}{\partial w_{j i}}=\delta_{j} x_{i}
\tag{5.53}
\end {align*}
本文では$x_i$ではなく$z_i$だが、今回は第1層を考えているため$x_i$となる。
\begin {align*}
\delta_{j}=h^{\prime}\left(a_{j}\right) \sum_{k} w_{k j} \delta_{k}
\tag{5.56}
\end {align*}
上の(5.53), (5.56)より、
\begin {align*}
\frac{\partial E_{n}}{\partial w_{j i}^{(1)}} = x_{i}h^{\prime}\left(a_{j}\right) \sum_{k} w_{k j}^{(2)} \delta_{k}
\tag{ex5.22.1}
\end {align*}
となる。このことと微分のチェーンルールを用いて、
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{j^{\prime} i^{\prime}}^{(1)}} =
\frac{\partial}{\partial a_{j^{\prime}}}\left(\frac{\partial E_{n}}{\partial w_{j i}^{(1)}}\right) \frac{\partial a_{j^{\prime}}}{\partial w_{j^{\prime} i^{\prime}}^{(1)}}
\tag{ex5.22.2}
\end {align*}
この(ex5.22.2)に関しては$h^{\prime}\left(a_{j}\right)$での微分が$j \neq j'$の場合と$j = j'$の場合で変わってくるため、$j \neq j'$の場合と$j = j'$の場合で分けて考えるのがよい。
- $j \neq j'$の場合
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{j^{\prime} i^{\prime}}^{(1)}} =
\sum_{k^{\prime}} \frac{\partial}{\partial a_{k^{\prime}}}\left(\frac{\partial E_{n}}{\partial w_{j i}^{(1)}}\right) \frac{\partial a_{k^{\prime}}}{\partial a_{j^{\prime}}} x_{i^{\prime}}
\end {align*}
\begin {align*}
\frac{\partial a_{k}^{\prime}}{\partial a_{j}^{\prime}}=w_{k^{\prime} j^{\prime}} h^{\prime}\left(a_{j^{\prime}}\right)
\end {align*}
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{j^{\prime} i^{\prime}}^{(1)}}=x_{i} x_{i^{\prime}} h^{\prime}\left(a_{j^{\prime}}\right) h^{\prime}\left(a_{j}\right) \sum_{k} \sum_{k^{\prime}} w_{k^{\prime} j^{\prime}}^{(2)} w_{k j}^{(2)} M_{k k^{\prime}}
\tag{5.94'}
\end {align*}
- $j = j'$の場合
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{j^{\prime} i^{\prime}}^{(1)}}=x_{i} x_{i^{\prime}}\sum_{k} w_{k j}\left\{\left(\frac{\partial}{\partial a_{j^{\prime}}} \frac{\partial E_{n}}{\partial a_{k}}\right) h^{\prime}\left(a_{j}\right)+\left(\frac{\partial}{\partial a_{j^{\prime}}} h^{\prime}\left(a_{j}\right)\right) \frac{\partial E_{n}}{\partial a_{k}}\right\}
\end {align*}
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{j^{\prime} i^{\prime}}^{(1)}}=x_{i} x_{i^{\prime}} h^{\prime \prime}\left(a_{j^{\prime}}\right) \sum_{k} w_{k j^{\prime}}^{(2)} \delta_{k}\\
\quad+x_{i} x_{i^{\prime}} h^{\prime}\left(a_{j^{\prime}}\right) h^{\prime}\left(a_{j}\right) \sum_{k} \sum_{k^{\prime}} w_{k^{\prime} j^{\prime}}^{(2)} w_{k j}^{(2)} M_{k k^{\prime}}
\tag{5.94"}
\end {align*}
よって、(5.94')と(5.94")の結果を合わせると、
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{j^{\prime} i^{\prime}}^{(1)}}=x_{i} x_{i^{\prime}} h^{\prime \prime}\left(a_{j^{\prime}}\right) I_{j j^{\prime}} \sum_{k} w_{k j^{\prime}}^{(2)} \delta_{k}\\
\quad+x_{i} x_{i^{\prime}} h^{\prime}\left(a_{j^{\prime}}\right) h^{\prime}\left(a_{j}\right) \sum_{k} \sum_{k^{\prime}} w_{k^{\prime} j^{\prime}}^{(2)} w_{k j}^{(2)} M_{k k^{\prime}}
\tag{5.94}
\end {align*}
が導かれる。
3.重みは1つの層に1つずつある:
\begin {align*}
\frac{\partial E_{n}}{\partial w_{j i}^{(1)}} = x_{i}h^{\prime}\left(a_{j}\right) \sum_{k} w_{k j}^{(2)} \delta_{k}
\tag{ex5.22.1}
\end {align*}
(ex5.22.1)を用いると、
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{k j^{\prime}}^{(2)}} =
\frac{\partial}{\partial w_{k j^{\prime}}^{(2)}}\left(\frac{\partial E_{n}}{\partial w_{j i}^{(1)}}\right)
\tag{ex5.22.3}
\end {align*}
今回も$w_{k j^{\prime}}^{(2)}$での微分が$j \neq j'$の場合と$j = j'$の場合で変わってくる。ただし今回は場合分けをせずに一気に行う。
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{k j^{\prime}}^{(2)}} =
x_{i} h^{\prime}\left(a_{j}\right)\left\{\left(\frac{\partial}{\partial w_{k j^{\prime}}^{(2)}} \sum_{k} w_{k j}^{(2)}\right) \delta_{k}+\left(\frac{\partial}{\partial w_{k j^{\prime}}^{(2)}} \delta_{k}\right) \sum_{k} w_{k j}^{(2)}\right\}
\end {align*}
これをまとめると、
\begin {align*}
\frac{\partial^{2} E_{n}}{\partial w_{j i}^{(1)} \partial w_{k j^{\prime}}^{(2)}}=x_{i} h^{\prime}\left(a_{j^{\prime}}\right)\left\{\delta_{k} I_{j j^{\prime}}+z_{j^{\prime}} \sum_{k^{\prime}} w_{k^{\prime} j^{\prime}}^{(2)} M_{k k^{\prime}}\right\}
\tag{5.95}
\end {align*}
以上で3つの結果を導くことができた。