非侵襲的治療に有効な音楽の特徴を抽出する

#背景
モーツァルトの曲は、**”Mozart Effect”**と知られる程に、非侵襲的治療の可能性について昔より研究されている。最近、薬物耐性てんかんの治療法として、モーツァルト「2台のピアノのためのソナタ ニ長調（K.448）」が有効であることを示唆する論文が掲載された（論文1）。とても気になったので、この曲の特徴をAutoencoderで抽出し、当該研究に活かせないか探ってみた。
作業フローは以下の通りである。

• 1. 学習データの作成
• 1. モデルの構築
• 1. 特徴抽出

##1. 学習データの作成
まずはK448を学習データにしていく。
###1‐1. 楽曲データの読み込み

import librosa
K448_original, sr = librosa.load("Sonata-K448-1.wav")#第1楽章のみ

サンプリングレートはデフォルトの22,050Hzにて行う。

###1‐2. データの整形
論文中では、K448を聞き始めてから30~45秒で効果が表れるそうなので、45秒毎に分割してみる。

s=sr*45
K448_45sec = []
for a in range(17):#13分弱あるので17個に分割できる
    a+=1
    K448_45sec.append(K448_original[a*s-s:a*s])
print(K448_45sec[0])

結果

array([0.        , 0.        , 0.        , ..., 0.03427124, 0.02934265,
       0.02760315], dtype=float32)

これだけでは学習データの量として不十分なため、水増しする。
###1-3. データの水増し
非常に興味深いことに、K448の有効性は変調やテンポ変更することで失われるらしい。このことより、水増しは、音量変更及びノイズ付加、残響付加のみとした。

因みに、同じ周波数や同じテンポの全く別の曲は有効性がなかったそうです！

import numpy as np
import random
from scipy.signal import fftconvolve

def scratch(m):
    musics=[m]
    ir_data ,_ = librosa.load("Kenny_s-Vocalverb.wav")#残響データ
    scratch=np.array([
        #音量変更
        lambda x:x*random.uniform(0.5, 1.5),
        #ノイズ付加（ホワイトノイズ）
        lambda x:x+random.uniform(0.001, 0.005)*np.random.randn(len(x)),
        #残響付加
        lambda x:fftconvolve(x,ir_data)[0:sr45]#47秒で出力されてしまったので     
    ])
    doubling_musics=lambda f,music:(music+[f(i) for i in music])
    for func in scratch:
        musics = doubling_musics(func,musics)
    return musics

scratch_K448_musics = [scratch(m) for m in K448_45sec]#ここで水増し
scratch_K448_musics = sum(scratch_K448_musics,[])#1次元化
print(len(scratch_K448_musics))

結果

136

17個から136個に増えました。

###1-4. データの水増し（無処理）
K448の有効性は多少のノイズや音量の違いで失われないと仮定し、今回作成するAutoencoderは、デノイズのモデルを参考にすることとした。そのため、無処理データも作成しておく必要がある。

def nonscratch(m):
    musics=[m]
    nonscratch=np.array([
        lambda x:x,
        lambda x:x,
        lambda x:x   
    ])
    doubling_musics=lambda f,music:(music+[f(i) for i in music])
    for func in nonscratch:
        musics = doubling_musics(func,musics)
    return musics

nonscratch_K448_musics = [nonscratch(m) for m in K448_45sec]
nonscratch_K448_musics = sum(nonscratch_K448_musics,[])
print(len(nonscratch_K448_musics))

結果

136

このデータがターゲットデータの役割を果たす。

###1-5. 波形出力
ここで、各水増しデータが元データと波形が異なることを確認してみる。

#代表として冒頭45秒とその水増しデータをリスト化
List_name = ["K448","K448_vol","K448_wn","K448_riv"]
List = [scratch_K448_musics[0],scratch_K448_musics[1],
        scratch_K448_musics[2],scratch_K448_musics[4]]
#波形出力
import matplotlib.pyplot as plt
import librosa.display
fig, ax = plt.subplots(nrows=1, ncols=4, sharex=True, sharey=True, figsize=(24, 3))
for i,(file_name,file) in enumerate(zip(List_name,List)):
    librosa.display.waveplot(file,sr=sr,ax=ax[i])
    ax[i].set(title=file_name,ylabel="amplitude")

左から、無処理、音量変更、ノイズ付加、残響付加である。比較しやすいようにy軸は統一している。図のように、各処理が正常に行われたことを確認できた。

###1-6. スペクトログラム化
Autoencoderの学習データには、スペクトログラム化したものを用いる。今回、人間が音を知覚する原理にできる限り近似する処理にしたいため、Constant-Q変換を用いて短時間フーリエ変換することとした。
先程、波形出力したデータと同じデータを短時間フーリエ変換し、スペクトログラムで確認してみる。
ライブラリにはlibrosa.cqtを用いる。

hop_length = 256
window = 'hann'
bins_per_octave = 12
n_octaves = 7
n_bins = bins_per_octave * n_octaves
List_cqt=[]

fig, ax = plt.subplots(nrows=1, ncols=4, sharex=True, sharey=True, figsize=(24, 3))
for i,(file_name,file) in enumerate(zip(List_name,List)):
    C = np.abs(librosa.cqt(file, sr=sr, hop_length = hop_length, fmin=librosa.note_to_hz('C1'), 
                         n_bins=n_bins,bins_per_octave=bins_per_octave, window=window))
    db = librosa.amplitude_to_db(C, ref=np.max)
    img = librosa.display.specshow(db, y_axis='cqt_hz', x_axis='time',sr=sr, hop_length=hop_length, ax=ax[i])
    ax[i].set(title=file_name)
    fig.colorbar(img, ax=ax[i], format="%+2.f dB")

波形出力では分かりずらかったノイズ付加の有無が一目瞭然である。

###1-7. データをConstant-Q変換
では、全データ（scratch_K448_musics及びnonscratch_K448_musics）をConstant-Q変換し、学習データとする。

List_cqt=[]
List_cqt_non=[]
for music in scratch_K448_musics:
    C = np.abs(librosa.cqt(music, sr=sr, hop_length = hop_length, fmin=librosa.note_to_hz('C1'), 
                         n_bins=n_bins,bins_per_octave=bins_per_octave, window=window))
    List_cqt.append(C)
    
for music in nonscratch_K448_musics:
    C = np.abs(librosa.cqt(music, sr=sr, hop_length = hop_length, fmin=librosa.note_to_hz('C1'), 
                         n_bins=n_bins,bins_per_octave=bins_per_octave, window=window))
    List_cqt_non.append(C)

arr_cqt=np.stack(List_cqt)
arr_cqt_non=np.stack(List_cqt_non)
print(arr_cqt.shape)
print(arr_cqt_non.shape)

結果

(136, 84, 3876)
(136, 84, 3876)

以上で学習データの作成は終了である。

##2. モデルの構築
上で述べたように、処理データと無処理データを学習させてAutoencoderを構築する。
ライブラリにはTensorFlowを用いる。
###2-1. Autoencoderの構築
Autoencoderの中では、encoderを通ってK448の特徴が抽出され、decoderを通って元のデータに復元（損失あり）している。復元後の損失値が小さくなるようにハイパラメーターを調整することで、K448の最適な特徴を抽出できるレイヤーの重みを作り出せる。

import tensorflow as tf
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers,losses
from tensorflow.keras.models import Sequential,Model
from tensorflow.keras.optimizers import Adam

cqt_re = arr_cqt.reshape(-1,84,3876,1)
cqt_non_re = arr_cqt_non.reshape(-1,84,3876,1)

train_data, test_data, train_non, test_non = train_test_split(
    cqt_re, cqt_non_re, test_size=0.2, random_state=21)

class Autoencoder(Model):
    def __init__(self):
        super(Autoencoder, self).__init__()
        self.encoder = tf.keras.Sequential([
            layers.Input(shape=(84,3876,1)),
            layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
            layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])

        self.decoder = tf.keras.Sequential([
            layers.Conv2DTranspose(8, (3, 3), strides=2, activation='relu', padding='same'),
            layers.Conv2DTranspose(16, (3, 3), strides=2, activation='relu', padding='same'),
            layers.Conv2D(1, (3, 3), activation='relu', padding='same')])

    def call(self, x):
        encoded = self.encoder(x)
        decoded = self.decoder(encoded)
        return decoded

model = Autoencoder()

optimizer = Adam(learning_rate=0.003)
model.compile(optimizer=optimizer,loss=losses.MeanSquaredError())
model.summary()
model.fit(train_data, train_non,
          batch_size=32,
          epochs=20,
          verbose=1,
          shuffle=True,
          validation_data=(test_data, test_non))

結果

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
sequential (Sequential)   (None, 21, 969, 8)        1320      
_________________________________________________________________
sequential_1 (Sequential)   (None, 84, 3876, 1)       1897      
=================================================================
Total params: 3,217
Trainable params: 3,217
Non-trainable params: 0
_________________________________________________________________

#最後だけ
Epoch 20/20
4/4 [==============================] - 1s 163ms/step - loss: 0.0036 - val_loss: 0.0045

次元削減できており、これ以上損失値を下げれなかったため、このモデルの性能を確認する。

###2-2. モデルの性能
どのくらい復元できるのか確認してみる。

#無処理データ同士で損失値を確認
model.evaluate(cqt_non_re, cqt_non_re, verbose=1)

結果

5/5 [==============================] - 0s 58ms/step - loss: 0.0027

無処理データ同士でも損失値がでることから、完全な復元はできていない。

###2-3. モデルの性能（スペクトログラム）
どのくらい復元できるのか可視化して確認してみる。

List_data=test_data[0:4].reshape(-1,84,3876)#テストデータの最初の4つ
List_decoded_data=model(test_data[0:4]).numpy().reshape(-1,84,3876)#モデルを通った後

fig, ax = plt.subplots(nrows=1, ncols=4, sharex=True, sharey=True, figsize=(24, 3))
for i,(data) in enumerate(List_data):
    db = librosa.amplitude_to_db(data, ref=np.max)
    img = librosa.display.specshow(db, y_axis='cqt_hz', x_axis='time',sr=sr, hop_length=hop_length, ax=ax[i])
    ax[i].set(title=i)
    fig.colorbar(img, ax=ax[i], format="%+2.f dB")

fig, ax = plt.subplots(nrows=1, ncols=4, sharex=True, sharey=True, figsize=(24, 3))
for i,(data) in enumerate(List_decoded_data):
    db = librosa.amplitude_to_db(data, ref=np.max)
    img = librosa.display.specshow(db, y_axis='cqt_hz', x_axis='time',sr=sr, hop_length=hop_length, ax=ax[i])
    ax[i].set(title=i)
    fig.colorbar(img, ax=ax[i], format="%+2.f dB")

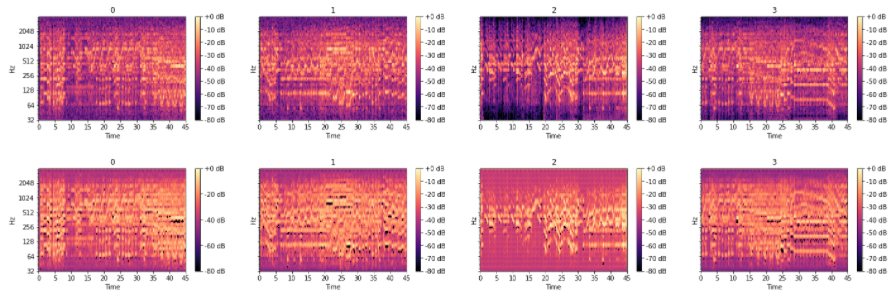
元のデータに近いところまで復元できていることがわかる。さらに、ノイズも消えていることから、強調された音以外は特徴に含まれていないと考察できる。復元度はコサイン類似度などで定量できるが、今回は割愛する。
改良の余地はあるが、以上でモデルの構築を終了とする。

##3. 特徴抽出
作成したモデルは、K448の特徴を抽出できるように調整されている。encoderの出力がそのまま特徴となる。
特徴を抽出して何ができるのか、、、これが今回の課題である。
単純な例ではあるが、思いついたことを箇条書きにしてみた。

• K448の特徴から有効性の高い新たな曲を作り出す。
• K448の特徴を解析し、有効な要素を解明する。
• K448の特徴と類似する曲を探す。

今回は最後の項目をやってみることにした。類似する曲、それ即ち、K448と同じ有効性のある曲とも解釈できる。ちゃんとやるならば、抽出したK448の特徴が本当に有効性を表しているのか確かめる必要はあるが、ここでは割愛します。今回は簡単に、コサイン類似度とユークリッド距離を用いて、特徴の類似性を判定してみる。

以下は、作成したモデルを使って、新たに4曲（冒頭45秒）の特徴を抽出し、K448（冒頭45秒）の特徴との類似性を算出している。

#論文で有効性が示されなかったワーグナーのローエングリン
Lohengrin_original, _ = librosa.load("Richard Wagner - Lohengrin Act 1 Prelude.wav")
#私の好きなメタル曲
cafo_original, _ = librosa.load("CAFO.wav")
#論文で有効性が示されなかったヴァイオレットノイズ
vn_original, _ = librosa.load("violetnoise.wav")
#K448と同じくピアノのベートーヴェンの月光
Moon_original, _ = librosa.load("Beethoven Moonlight.wav")

Lohengrin =Lohengrin_original[0:sr45]
cafo =cafo_original[0:sr45]
vn =vn_original[0:sr45]
Moon =Moon_original[0:sr45]

Lohengrin_cqt = np.abs(librosa.cqt(Lohengrin, sr=sr, hop_length = hop_length, fmin=librosa.note_to_hz('C1'), 
                         n_bins=n_bins,bins_per_octave=bins_per_octave, window=window))
cafo_cqt = np.abs(librosa.cqt(cafo, sr=sr, hop_length = hop_length, fmin=librosa.note_to_hz('C1'), 
                         n_bins=n_bins,bins_per_octave=bins_per_octave, window=window))
vn_cqt = np.abs(librosa.cqt(vn, sr=sr, hop_length = hop_length, fmin=librosa.note_to_hz('C1'), 
                         n_bins=n_bins,bins_per_octave=bins_per_octave, window=window))
Moon_cqt = np.abs(librosa.cqt(Moon, sr=sr, hop_length = hop_length, fmin=librosa.note_to_hz('C1'), 
                         n_bins=n_bins,bins_per_octave=bins_per_octave, window=window))

fig, ax = plt.subplots(nrows=1, ncols=4, sharex=True, sharey=True, figsize=(24, 3))

db = librosa.amplitude_to_db(Lohengrin_cqt, ref=np.max)
img = librosa.display.specshow(db, y_axis='cqt_hz', x_axis='time',sr=sr, hop_length=hop_length, ax=ax[0])
ax[0].set(title="Lohengrin")
fig.colorbar(img, ax=ax[0], format="%+2.f dB")

db = librosa.amplitude_to_db(cafo_cqt, ref=np.max)
img = librosa.display.specshow(db, y_axis='cqt_hz', x_axis='time',sr=sr, hop_length=hop_length, ax=ax[1])
ax[1].set(title="cafo")
fig.colorbar(img, ax=ax[1], format="%+2.f dB")

db = librosa.amplitude_to_db(vn_cqt, ref=np.max)
img = librosa.display.specshow(db, y_axis='cqt_hz', x_axis='time',sr=sr, hop_length=hop_length, ax=ax[2])
ax[2].set(title="vn")
fig.colorbar(img, ax=ax[2], format="%+2.f dB")

db = librosa.amplitude_to_db(Moon_cqt, ref=np.max)
img = librosa.display.specshow(db, y_axis='cqt_hz', x_axis='time',sr=sr, hop_length=hop_length, ax=ax[3])
ax[3].set(title="Moon")
fig.colorbar(img, ax=ax[3], format="%+2.f dB")

Lohengrin_data = Lohengrin_cqt.reshape(-1,84,3876,1)
cafo_data = cafo_cqt.reshape(-1,84,3876,1)
vn_data = vn_cqt.reshape(-1,84,3876,1)
Moon_data = Moon_cqt.reshape(-1,84,3876,1)

#K448の冒頭45秒とモデルの性能で確認したテストデータ3番目を追加して、特徴抽出
K448_0_feature=model.encoder(arr_cqt_non[0].reshape(-1,84,3876,1)).numpy().reshape(-1)
K448_test2_feature=model.encoder(test_data[2].reshape(-1,84,3876,1)).numpy().reshape(-1)
Lohengrin_feature=model.encoder(Lohengrin_data).numpy().reshape(-1)
cafo_feature=model.encoder(cafo_data).numpy().reshape(-1)
vn_feature=model.encoder(vn_data).numpy().reshape(-1)
Moon_feature=model.encoder(Moon_data).numpy().reshape(-1)

#コサイン類似度でK448の冒頭45秒に対する類似性を判定
from scipy import spatial
result_0_K448 = 1 - spatial.distance.cosine(K448_0_feature,K448_0_feature)
result_test2_K448 = 1 - spatial.distance.cosine(K448_0_feature,K448_test2_feature)
result_cafo = 1 - spatial.distance.cosine(K448_feature,cafo_feature)
result_Lohengrin = 1 - spatial.distance.cosine(K448_feature,Lohengrin_feature)
result_vn = 1 - spatial.distance.cosine(K448_feature,vn_feature)
result_Moon = 1 - spatial.distance.cosine(K448_feature,Moon_feature)

print('K448冒頭:',result_K448,'\n',
      'K448途中:',result_test2_K448,'\n',
      'cafo:',result_cafo,'\n',
      'Lohengrin:',result_Lohengrin,'\n',
      'vn:',result_vn,'\n',
      'Moon:',result_Moon)

#ユークリッド距離でK448の冒頭45秒に対する類似性を判定
result_0_K448 = spatial.distance.euclidean(K448_0_feature,K448_0_feature)
result_test2_K448 = spatial.distance.euclidean(K448_0_feature,K448_test2_feature)
result_cafo = spatial.distance.euclidean(K448_0_feature,cafo_feature)
result_Lohengrin = spatial.distance.euclidean(K448_0_feature,Lohengrin_feature)
result_vn = spatial.distance.euclidean(K448_0_feature,vn_feature)
result_Moon = spatial.distance.euclidean(K448_0_feature,Moon_feature)

print('K448冒頭:',result_0_K448,'\n',
      'K448途中:',result_test2_K448,'\n',
      'cafo:',result_cafo,'\n',
      'Lohengrin:',result_Lohengrin,'\n',
      'vn:',result_vn,'\n',
      'Moon:',result_Moon)

結果

#コサイン類似度
K448冒頭: 1 
K448途中: 0.5028753280639648 
cafo: 0.21718403697013855 
Lohengrin: 0.3516264259815216 
vn: 0.2888488471508026 
Moon: 0.4304010272026062

#ユークリッド距離
K448冒頭: 0.0 
K448途中: 52.56835174560547 
cafo: 606.96435546875 
Lohengrin: 57.18647766113281 
vn: 57.5987434387207 
Moon: 55.03040313720703

K448同士で類似性が最も高く、次いでピアノ曲という結果となり、それっぽい傾向が表れた。

#まとめ
Autoencoderにより、K448の特徴抽出ができ、その利用手段についても実践を交えて確認できた。また、今回のモデルの中間層は全結合しておらず、それほど圧縮率は高くない。全結合した場合、楽曲ジャンルとしての特徴に集約されてしまい、有効性の特徴が失われることを恐れたからである。そのため、先程も述べたように、抽出したK448の特徴が本当に有効性を表しているのか確かめる必要はある。

実は、過去の論文でK448以外にK545も抗てんかん作用を持つことで知られており（論文2）、この2曲を用いてモデルを再構築すれば、より有効な特徴を抽出できるかもしれない。