閉ループステップ応答データを用いたデータドリブンな周波数応答推定(MATLAB編)

はじめに

制御系設計のもっとも基本的なアプローチは、一巡伝達関数の周波数応答をプロットして制御系が不安定化しないようにゲイン余裕と位相余裕を調整することです。ゲイン余裕と位相余裕に関する目安もいくつか示されており、この方法を使うことで意味のある思考錯誤によってフィードバック制御器のゲインを調整できます。しかしながら、この方法を使う場合には一巡伝達関数の周波数応答を利用する関係上、「制御対象の周波数応答」をなんらかの方法で取得しなければなりません。周波数応答を直接測定できない場合、時系列データから周波数応答を推定しなければいけません。最もリーズナブルなアプローチは「操業データに対して離散フーリエ変換を施して周波数応答を推定する」ことになります。既に得られている操業データを周波数応答に変換できれば、古典制御の枠組みでリーズナブルにゲイン設計できるでしょう。

しかしながら、離散フーリエ変換による周波数応答の推定はどんな時系列データでも扱えるわけではありません。例えば、目標値がステップ指令となるような閉ループ応答データを用いて周波数応答推定することは困難です。産業現場では目標値をステップ波として与える事がかなり多く、そのような閉ループ応答データしか手元にないということも珍しくありません。このような場合、どのように操業データから周波数応答を推定すれば良いでしょうか？ 以上の背景のもと、今回は閉ループステップ応答データから制御対象の周波数応答を推定する手法をご紹介します。MATLABを用いたサンプルコードも用意し、簡単な数値例を通して周波数応答を推定の効果を解説していきます。本記事を執筆するにあたり、下記の論文を参考にさせていただきました。もしご興味あれば一読いただけるとより理解が深まると思います。

「松井義弘, 綾野秀樹, 増田士朗, & 中野和司. (2020). 閉ループデータから時間および周波数領域で推定した制御対象のインパルス応答の比較. 電気学会論文誌 C (電子・情報・システム部門誌), 140(3), 340-341.」
「松井義弘, 綾野秀樹, 増田士朗, & 中野和司. (2023). 非零の定常値を持つ過渡応答信号の周波数特性推定法. 電気学会論文誌 C (電子・情報・システム部門誌), 143(3), 250-257.」
「松井義弘, & 中野和司. (2013). 周波数領域の情報を併用した閉ループ過渡応答データからの制御器調整. 計測と制御, 52(10), 892-897.」

問題設定

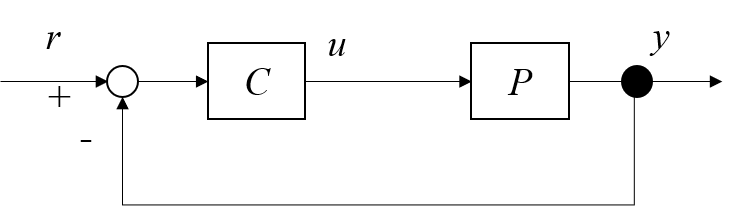
Fig.1のフィードバック制御系を考えます。目標値$r$はステップ信号として設定されております。今回のケースでは、目標値$r$を印加した際に得られる有限時間の入出力データ$u_{0}$と$y_{0}$が操業データとして獲得できるとします。ここで、獲得済みの操業データは初期値と最終値が定常状態であるとします。時間信号は固定サンプルで得られた有限時間信号とします。$u_{0}$と$y_{0}$の時系列データを用いて、Fig.1の制御対象$P$の周波数応答を導出することを目指します。

　　　　　　　　　　　　　　　　　　Fig.1 SISOの制御系

離散フーリエ変換による周波数応答推定

離散フーリエ変換を用いた周波数応答推定の原理に関して説明します。そもそも周波数応答とは「正弦波を印加した際の定常特性」でした。過渡特性を含まないため、入出力の周波数成分の比が制御対象の周波数応答に相当します。つまり、入出力の時系列データを周波数成分のデータに変換し、その比を取るだけで周波数応答を導出できるのです。それでは、どのようにすれば時系列データを周波数成分に変換できるのでしょうか？時系列データを周波数成分に変換する方法こそが離散フーリエ変換です。離散フーリエ変換の具体的な手順を説明すると記事が膨大になってしまうので、本記事では手順を省略します。ここでは離散フーリエ変換を「時系列データを周波数成分に変換する関数」と思っていただければ大丈夫です。

離散フーリエ変換を用いて制御対象の周波数応答を導出する手順を述べます。まず、以下の二つの仮定を満たす有限時間の入出力データを用意します。

A.1
時間信号がそのデータ長を基本周期とする周波数信号として捉えても問題ない。
A.2
各時間信号は絶対過積分である。

絶対可積分が何なのかに関しては後ほど解説いたします。もし入出力データが上記の仮定を満たすのであれば、離散フーリエ変換を用いた周波数成分への変換を施すことができます。つまり、制御対象の周波数応答$P_{e}(j\omega)$は入出力データの離散フーリエ変換の比

P_{e}(j\omega)=\frac{\mathcal{F}[y_{0}]}{\mathcal{F}[u_{0}]}

と表現できます。$\mathcal{F}$は離散フーリエ変換の関数です。この結果からわかるように、離散フーリエ変換さえできてしまえば、制御対象の周波数応答を導出することはそこまで難しくありません。離散フーリエ変換自体も後述のサンプルコードではMATLABの関数を使って簡単に計算できてしまいます。もちろん、Python等でも離散フーリエ変換の関数を使えば簡単に実装できます。以上が離散フーリエ変換による周波数応答推定の手順でした。

離散フーリエ変換の課題

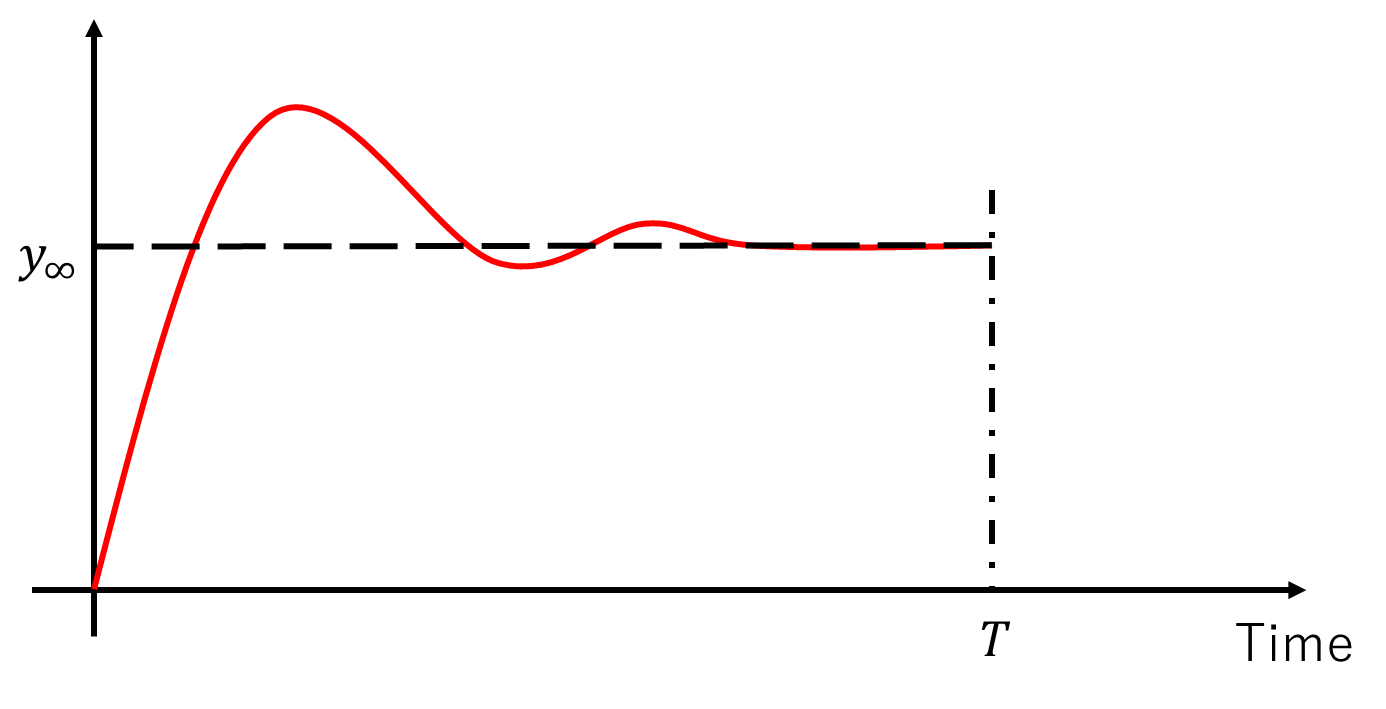
離散フーリエ変換による周波数応答推定は、仮定A.1とA.2を満たす入出力の時間信号が必要となります。問題設定で述べた「閉ループステップ応答データ」はこの仮定を満たすのでしょうか？まず、仮定A.1を満たすかどうか考えてみましょう。例えば、ステップ信号を目標値として印加した際のFig.2のような閉ループ応答の出力信号データを考えます。この信号は初期値が0、最終値(定常値)が$y_{\infty}$となっています。データ長は$T$としています。

　　　　　　　　　　　　　　　　Fig.2 閉ループステップ応答データの例

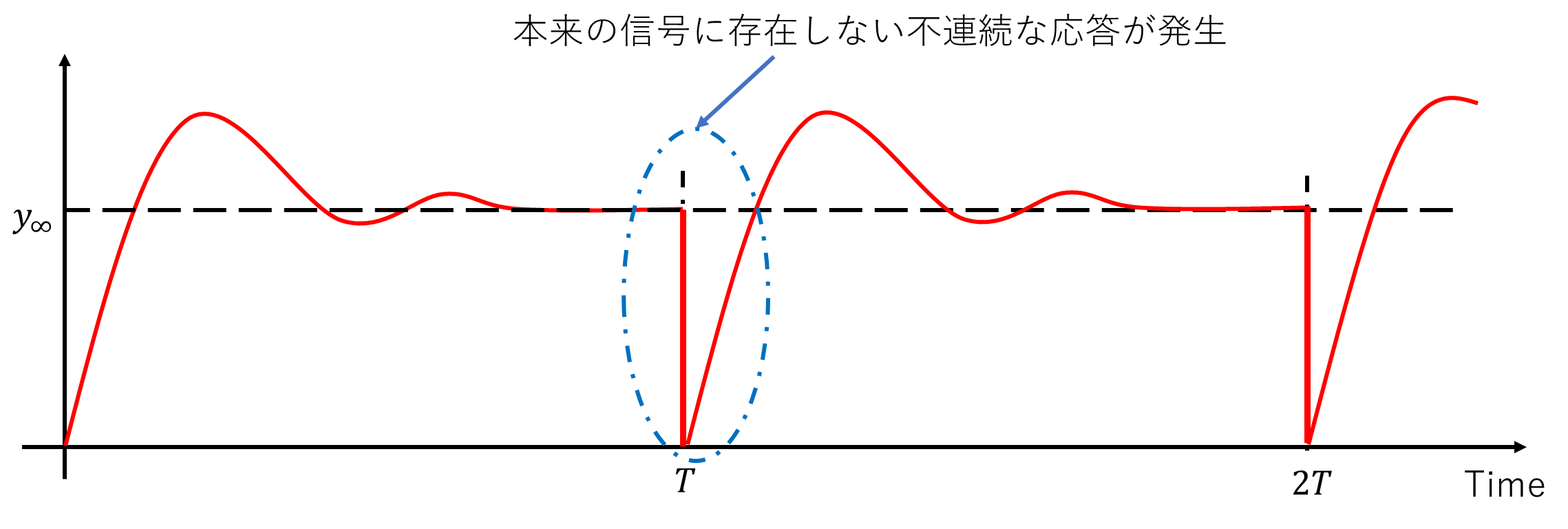
離散フーリエ変換のA.1の仮定とは、「時間信号がそのデータ長を基本周期とする周波数信号として捉えても問題ない」でした。なぜこのような仮定が必要になるのかというと、離散フーリエ変換は時間信号をそのまま周波数成分に変換しているわけではないからです。厳密には、「有限時間の時間信号を周期信号に変換し、その周期信号の周波数成分を算出している」が正しいです。つまり、Fig.2の時間信号に対して離散フーリエ変換の関数$\mathcal{F}$を施すということは、Fig.2を下記のFig.3の信号に直した上で周波数成分を得ることに相当します。Fig.3はFig.2の時間信号を一周期の信号とした際の周期信号となります。Fig.3を見ると、本来の信号に存在しない不連続な応答波形が生じていることがわかります。これは、Fig.2の初期値と最終値(定常値)が異なるためです。周期$T$の度に$y_{\infty}$から0に不連続な応答が生じてしまい、この高周波数成分が周波数応答の推定精度を悪化させてしまいます。以上の理由から、閉ループステップ応答はA.1の仮定を満たさないことがわかります。

　　　　　　　　　　　　　　　　Fig.3 離散フーリエ変換で扱われる周期信号

次に、A.2の仮定を満たすかどうかを確認しましょう。そもそも、絶対可積分とは何でしょうか？ここでは数学的な厳密性を抜きにして解説していきます。時間信号の関数を$f(t)$と定義します。$f(t)$が絶対可積分であれば、下記の式が成り立ちます。

\int_{-\infty}^{\infty} |f(t)| dt<\infty

Fig.2の時間信号の関数を$f(t)$とした際に、上記の式を満たすことができるのでしょうか？ 結論から言えば、Fig.2の信号を関数として考えると$f(\infty)=y_{\infty}$となってしまい、この関数を無限区間で積分すると値が発散してしまいます。したがって、上式を満たすことができないため、閉ループステップ応答データは絶対可積分な関数ではないということになります。ここまでの議論をまとめると、下記のようになります。

1.離散フーリエ変換では「時間信号がそのデータ長を基本周期とする周波数信号として捉えても問題ない」かつ「時間信号が絶対過積分である」を満たさなければ、適切な周波数成分への変換がなされない。

2.閉ループステップ応答データを周期信号として解釈すると、本来の信号に存在しない不連続な波形が現れてしまい、周波数応答の推定精度を悪化させてしまう。

3.閉ループステップ応答データは定常状態において、$f(\infty)=y_{\infty}$となってしまうことから絶対可積分な関数ではない。

結論として、閉ループステップ応答データの信号を離散フーリエ変換にて周波数成分に変換することはできないということになります。何らかの方法で入出力データに前処理を施し、離散フーリエ変換にて周波数応答を推定できるようにしなければなりません。

閉ループステップ応答データを用いた周波数応答推定

閉ループステップ応答データから周波数応答を導出する手法をご紹介します。前節の課題を解決する方法として、「入出力データに前処理を施す」ことが考えられます。言い換えると、「時間信号がそのデータ長を基本周期とする周波数信号として捉えても問題ない」かつ「時間信号が絶対過積分である」を満たすように入出力データを別の時間信号にあらかじめ変換するということです。いくつかの方法が提案されていますが、ここでは差分フィルタを用いる方法をご紹介します。

まず、差分フィルタの伝達関数$H$を

H=1-z^{-1}

定義します。このフィルタは現時刻の値と一サンプル時間前の値の差分を出力とするもっとも単純なフィルタです。獲得済みの入出力データ$y_{0}$と$u_{0}$に対して下記のように差分フィルタを施します。

y_{e}= H y_{0}

u_{e}= H u_{0}

この差分フィルタの出力$y_{e}$と$u_{e}$は定常値が0となるような関数となるため、絶対可積分とみなすことができます。さらに、初期値と定常値が両方とも0となるため、周期信号として解釈した際にもFig.3のような不連続な応答が生じません。この信号を用いることにより、制御対象の周波数応答を下記の式から計算できます。

P_{e}(j\omega)=\frac{\mathcal{F}[y_{e}]}{\mathcal{F}[u_{e}]}

ここまでの手順は下記のようにまとめることができます。

1.差分フィルタ$H$を定義する。

2.差分フィルタを施した出力$y_{e}$と$u_{e}$を計算する。

3.手順2で得られた信号データを用いて周波数応答を$P_{e}(j\omega)=\frac{\mathcal{F}[y_{e}]}{\mathcal{F}[u_{e}]}$と計算する。

本手順により、閉ループステップ応答データから周波数応答を計算できます。手順としては非常に簡単であり、ユーザーが設定すべき設計要素も存在しません。ただし、このアプローチは入出力データに含まれる高周波ノイズの悪影響を受けやすいという欠点があります。差分フィルタによる処理は前進差分の微分を施していることに相当します。もし入出力信号にノイズが含まれている場合、ノイズの影響が差分フィルタによって増幅してしまいます。このようなデータを用いて周波数応答を計算すると、ノイズの悪影響によって高周波数帯域の周波数応答の推定精度が劣化してしまうことがあります。本課題を解決する場合は差分フィルタではなく、バンドパスフィルタを用いて$y_{e}$と$u_{e}$を計算する必要があります。なお、大概のシステム同定手法では何らかの方法でノイズの影響を前処理しておくことが一般的のため、本手法固有の課題というわけないことにご注意ください。

Matlabによるデモ

それでは例題を通して、実際に周波数応答推定のデモをしてみましょう。簡単な例として次の対象に対する周波数応答推定問題を考えてみましょう。制御対象の伝達関数を

P=\frac{2}{(s+1)^{3}} e^{-0.15s}

と設定します。また、制御器を一般的なPID制御器：

C=K_{P}+\frac{K_{I}}{s}

としました。本例題では、PIDゲインの値は$K_{P}=1$、$K_{I}=0.25$と設定しました。今回は開ループ実験することができず、上記のPID制御器$C$を使った閉ループ実験でしか制御対象のデータを得ることができません。以上の問題設定のもと、閉ループステップ応答データから制御対象$P$の周波数応答を推定することを目指しましょう。

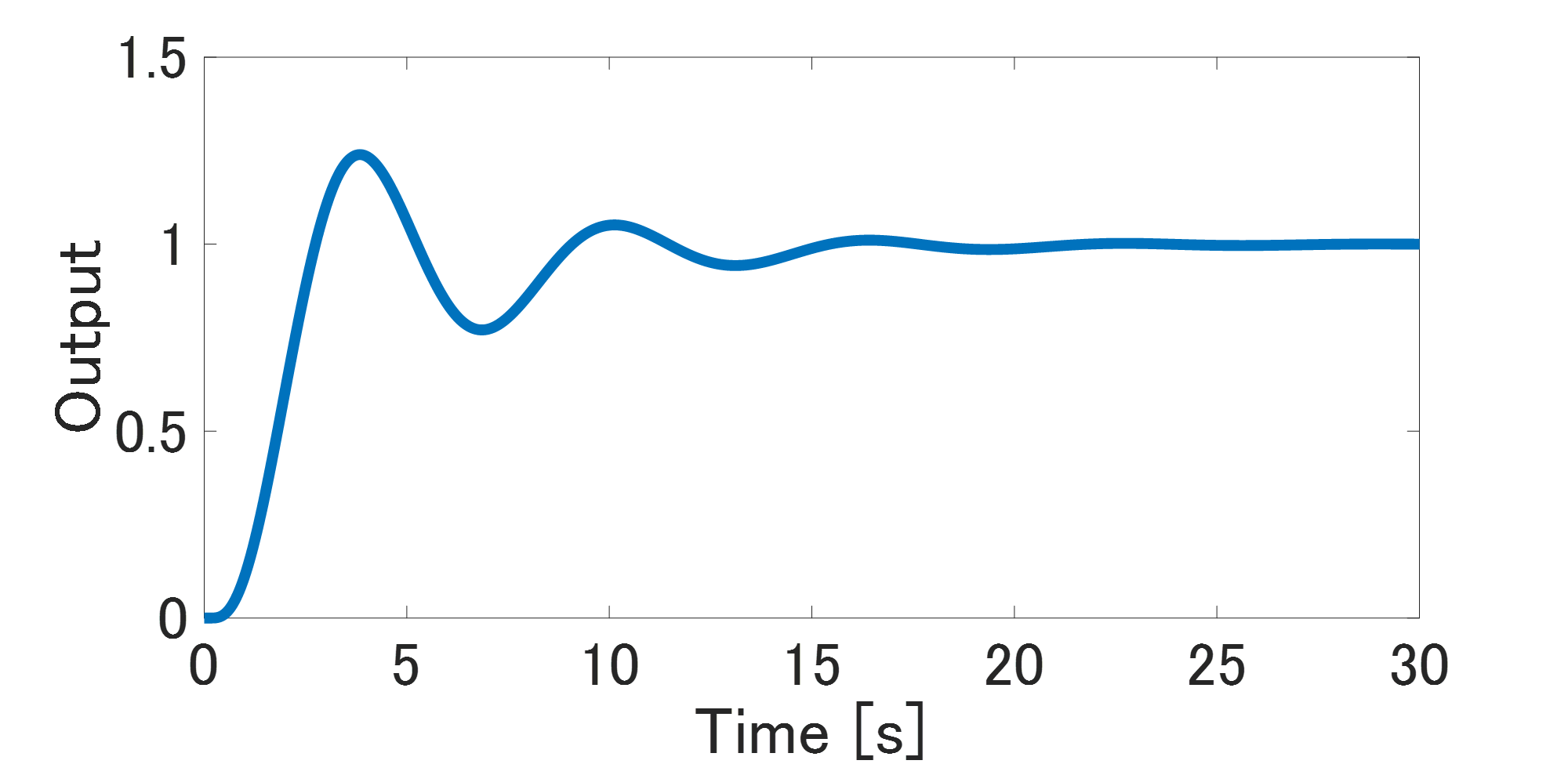
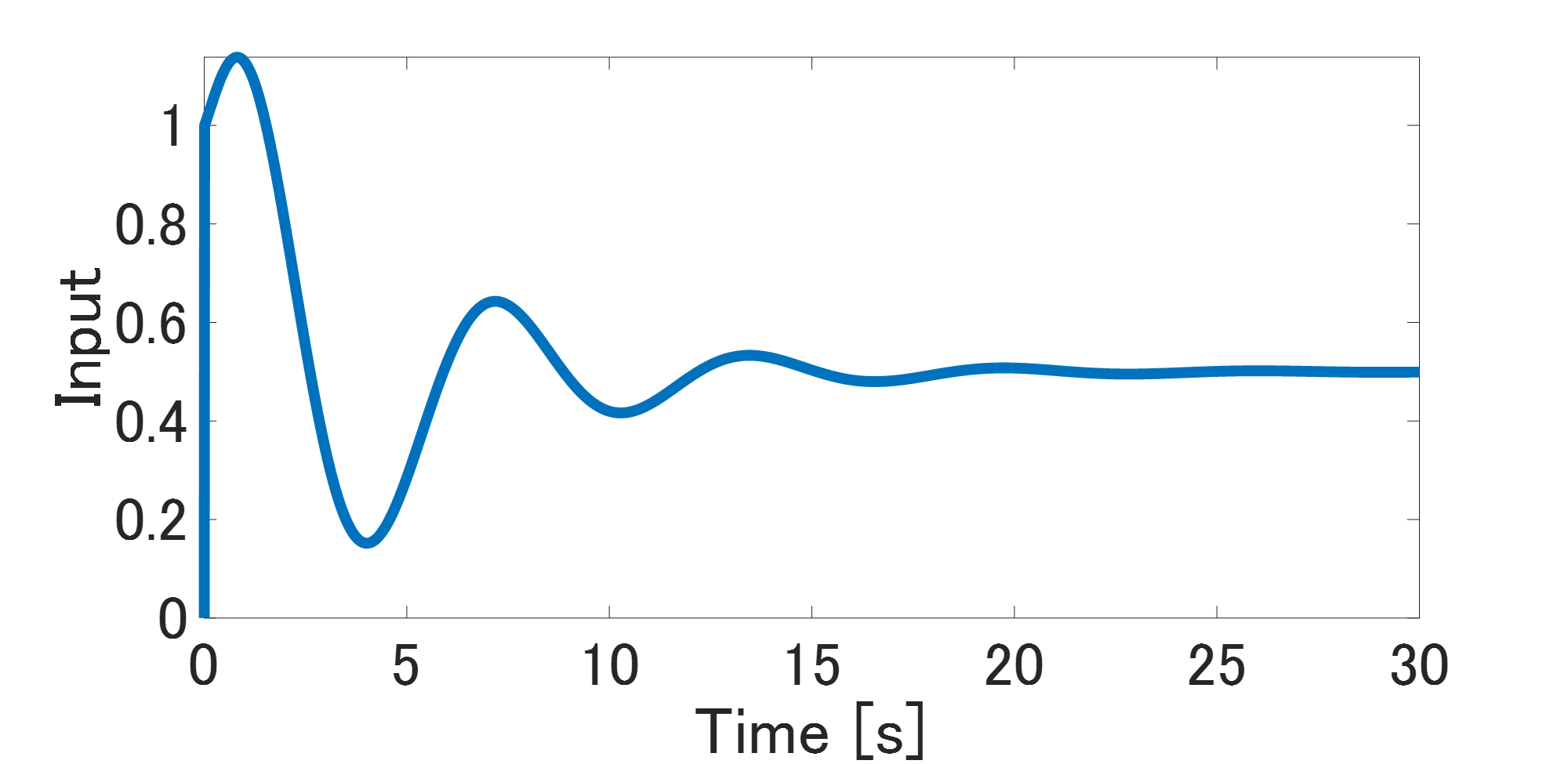
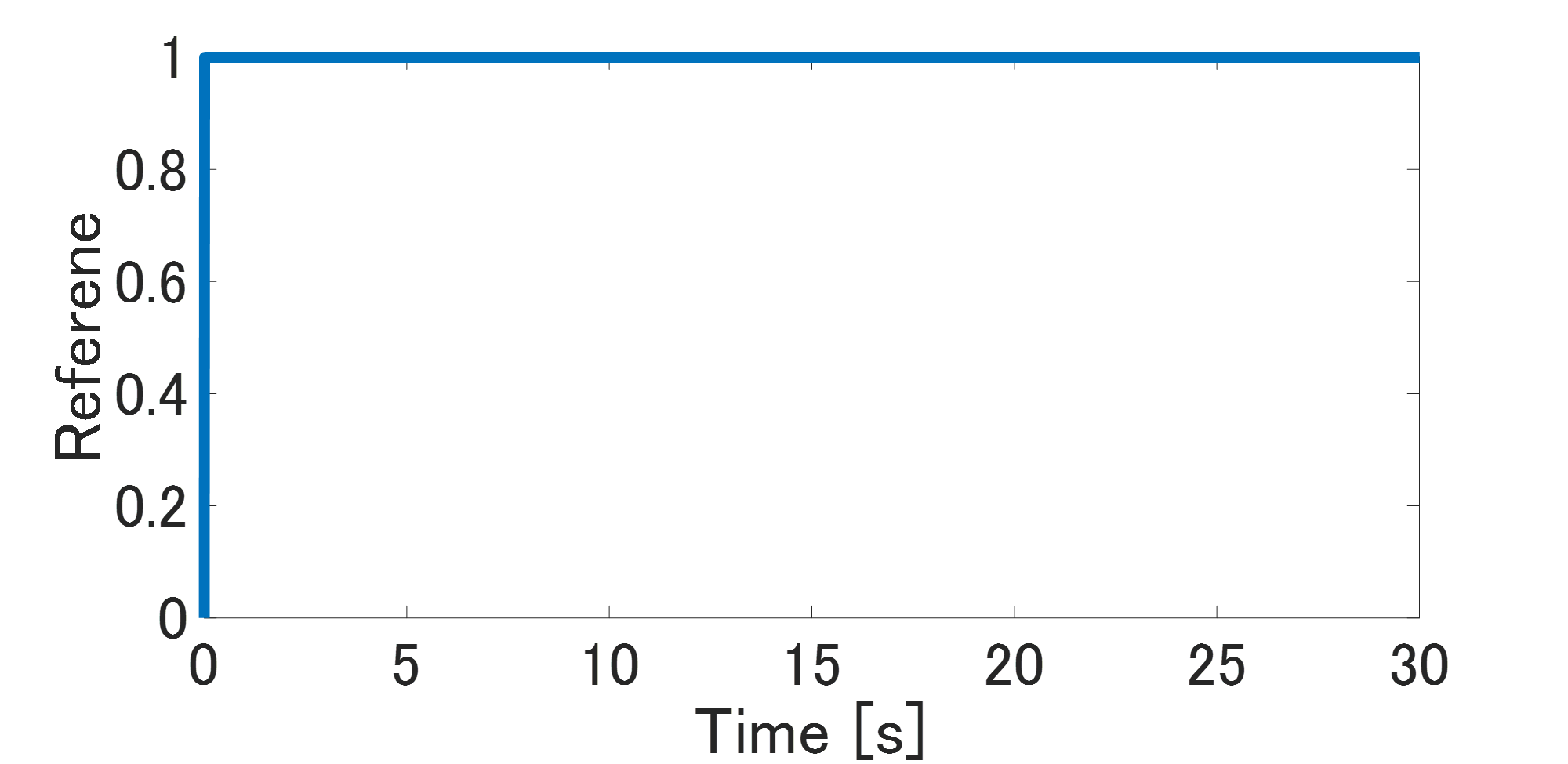
まず、閉ループ応答データを測定します。PID制御器を使った閉ループ実験にて、入出力応答を測定します。Fig.4とFig.5が実験時の閉ループ応答です。ここでは、Fig.6の単位ステップ信号を目標値としています。この時系列データを使って制御対象の周波数応答を離散フーリエ変換にて推定します。ここでは、Matlabのm-fileで作成したプログラムを用いて周波数応答を推定し、真値と推定値を比較してみます。

　　　　　　　　　　　　　　　　　　Fig.4 出力データ

　　　　　　　　　　　　　　　　　　Fig.5 入力データ

　　　　　　　　　　　　　　　　　　Fig.6 目標値

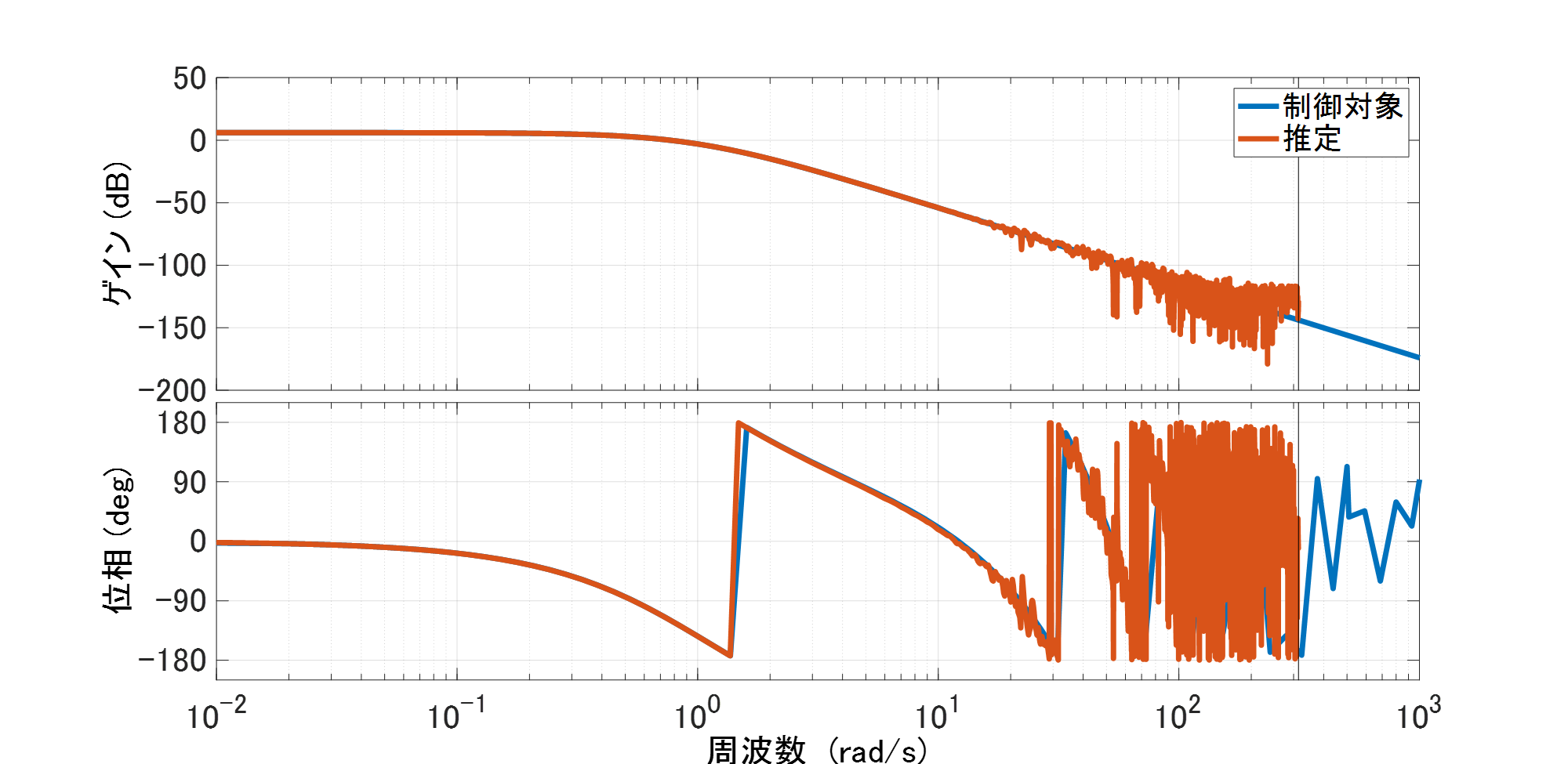
Fig.7が差分フィルタと離散フーリエ変換にて推定した周波数応答と真値の比較結果です。ほんの少し高周波数帯域で乖離が生じていますが、制御対象のロールオフ特性と一致していることがわかります。以上の結果から、閉ループステップ応答データから制御対象の周波数応答を推定できました。

　　　　　　　　　　　　　Fig.7 周波数応答(青：真値、赤：推定値)

おわりに

今回は、未知システムの周波数応答を閉ループステップ応答データから簡単な手順で推定する方法について解説しました。本記事で解説した手法はあくまで周波数応答推定の一手法でしかなく、他にも有望な手法は多数提案されています。しかしながら、本アプローチは入出力データに混入したノイズの影響がそこまで大きくなければ、制御対象の事前情報が余り得られない状況でも、ある程度の精度を有する周波数応答を推定できるという利点があります。もしご興味あれば、皆様の業務・研究でも活用してみてください。

サンプルコード

Matlabで作ったサンプルコードを記載しておきます。このプログラムを使うと、制御対象の周波数応答を計算できます。MATLAB(R2021a)とControl System Toolboxで動作確認しております。差分フィルタ自体はControl system Toolboxを使わなくても実装できるため、スクリプトを少し改造すればMATLABのみで運用することも可能です。

%% 初期実験データ生成
P=tf(2,[1,1])*tf([1],[1,1])*tf([1],[1,1],'InputDelay',0.15);%制御対象
C=tf(1,1)+tf([0.25],[1 0]);% PI制御器
t=(0:0.01:39)';% シミュレーション時間
r=ones(1,length(t));% 目標値
r(1)=0;

y=lsim(P*C/(1+P*C),r,t);%出力信号
u=lsim(C/(1+P*C),r,t);%入力信号

%% 差分フィルタを用いた周波数応答推定
df=tf([1 -1],[1 0],0.01);%差分フィルタ
ue=lsim(df,u,t);%差分フィルタ処理:入力
ye=lsim(df,y,t);%差分フィルタ処理:出力
Pe=fft(ye)./fft(ue);%離散フーリエ変換による周波数応答推定