はじめに
制御系設計成功の秘訣は「制御対象のモデリング」であることは多くの方が理解していることでしょう。運動方程式や回路方程式が既知であれば,物理原理からモデリングできるかもしれません。そうでなくとも,制御対象の次数情報が既知であれば,開ループ実験データを用いたパラメータ同定にてモデル獲得できるでしょう。同定モデルから周波数特性を導けば、古典制御に基づく安定性を保証可能な制御器を設計できます。
では,制御対象の次数が未知の場合は一体どうすればよいでしょうか?また,システム同定をするにしても,実験システムの都合上閉ループ実験データしか得られないことも多いと思います。対象によっては直接周波数応答を測定することも難しいでしょう。どのようにすれば,良好なモデルや周波数特性を得ることができるでしょうか?
本記事では,未知システムのモデルを実験データから簡単な手順で同定する方法について解説します。特に,ノンパラメトリックモデルの一つであるFIRフィルタに基づくモデリングアプローチについて解説してきます。
問題設定
まず,今回対象とするシステムを定義します。Fig.1のフィードバック制御系を考えます。制御対象を未知の次数を有する線形時不変システムとしています。今回は閉ループ実験にて,有限の入出力データ$u_{0}$と$y_{0}$が得られるとします。この実験データのデータ長は$N$とします。このデータを用いて制御対象$P$からノミナルモデル$P_{m}$を何らかの方法で導出することを目指します。ただし,実験データには観測ノイズ$d$が混ざっているため,同定モデルがノイズの影響を受けないようにしなければいけません。
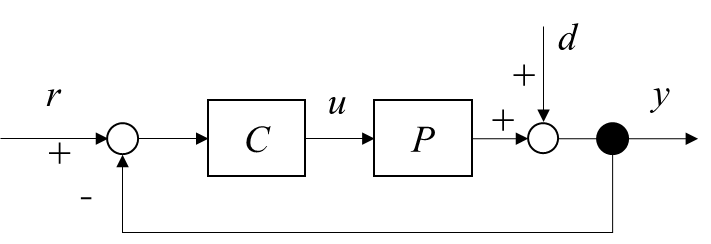
Fig.1 制御系のブロック線図
※なお,今回はあえてPE性に関する議論はせず,閉ループ実験データでも制御対象の特性が十分励起されているという前提のもと議論をすすめていきます。実際の閉ループ実験データにおける同定問題に関する踏み込んだ議論に興味のある方は,例えば下記の文献等を参考にしてみてください。
参考文献
1.松井義弘, 木村知彦, & 中野和司. (2011). 閉ループステップ応答データを用いた機械系の周波数応答推定. 電気学会論文誌 C (電子・情報・システム部門誌), 131(4), 751-757.
2.松井義弘, 綾野秀樹, 増田士朗, & 中野和司. (2019). 閉ループ応答データを用いた有限インパルス応答推定に基づく制御器調整法. 電気学会論文誌 C (電子・情報・システム部門誌), 139(8), 858-865.
3.松井義弘, 綾野秀樹, 増田士朗, & 中野和司. (2020). 閉ループデータから時間および周波数領域で推定した制御対象のインパルス応答の比較. 電気学会論文誌 C (電子・情報・システム部門誌), 140(3), 340-341.
モデリングアプローチ
本章では,ノンパラメトリックモデルアプローチにて制御対象をモデリングする方法について解説します。ここでは,インパルス応答の特性を利用することで制御対象$P$からノミナルモデル$P_{m}$を導出することを目指します。
インパルス応答推定に基づくモデリング
制御工学では,ステップ応答・インパルス応答・ランプ応答といった応答解析手法が非常に重要となります。このうちインパルス応答の特性として,「インパルス応答をラプラス変換することで伝達関数を導出できる」といったものがあります。何らかの方法でインパルス応答を獲得できれば,それをそのまま制御対象の伝達関数として扱えるわけです。この特性を利用したノンパラメトリックモデルがFIRフィルタです。FIRフィルタは有限区間のインパルス応答例を用いて
P_m (ρ)=\sum_{k=0}^{N}p(i)z^{-i}
と表現します。可調整パラメータ$ρ$は,制御対象のインパルス応答列$ρ=[p(0), p(1),….. p(N)]^T$です。初期実験データのデータ点数が$N$なので,FIRフィルタのタップ数も$N$となります。このモデルを活用することにより,有限区間のインパルス応答さえ導出できれば次数が未知の制御対象もモデリングが可能となるのです。
※ただし,FIRフィルタが制御対象の応答特性を模擬できるのは,データ点数が$N$となる区間のみです。それ以降は性能保証されないため,ご注意ください。
このアプローチで肝心な点は,「インパルス応答列$ρ=[p(0), p(1),….. p(N)]^T$をどのように算出するか?」といった点にあります。今回はインパルス入力を制御対象に印加できないため、別の手段を取る必要があります。もっとも簡単なアプローチは最小二乗法を利用することです。上記のFIRフィルタに初期実験で取得した初期制御入力$u_{0}$を印加することを考えましょう。FIRフィルタの特性として,FIRフィルタの出力を時間領域で表現すると,
\begin{aligned}
P_m(\rho) u_{0} &=\sum_{i=0}^N p(i) z^{-i} u_{0} \\
&=\left[\begin{array}{cccc}
u_{0}(0) & 0 & 0 & 0 \\
u_{0}(1) & u_{0}(0) & 0 & 0 \\
\vdots & \cdots & \ddots & \vdots \\
u_{0}(N) & \cdots & u_{0}(1) & u_{0}(0)
\end{array}\right] \rho \\
&=A \rho
\end{aligned}
と表現できることが知られています。$A$は正方行列:
\begin{aligned}
A =\left[\begin{array}{cccc}
u_{0}(0) & 0 & 0 & 0 \\
u_{0}(1) & u_{0}(0) & 0 & 0 \\
\vdots & \cdots & \ddots & \vdots \\
u_{0}(N) & \cdots & u_{0}(1) & u_{0}(0)
\end{array}\right] \\
\end{aligned}\in \mathbb{R}^{N+1 \times N+1}
となります。したがって,初期入力$u_{0}$を印加した際のFIRフィルタの出力が$y_{0}$と一致すれば,FIRフィルタと制御対象の応答特性が一致する(FIRフィルタの内包する$p$がインパルス応答の真値と一致する)ことになります。つまり,評価関数
J_{FIR}(\rho)=\left\|y_{0}-P_{m}(\rho) u_{0}\right\|^{2}
を最小化すればよいわけです。この評価関数に$P_m(\rho)u_{0}=A\rho$と$Y=y_{0}$の関係式を代入することにより,上記の評価関数を
J_{FIR}(\rho)=\left\|Y-A\rho\right\|^{2}
と等価変換できます。この評価関数の形に見覚えのある方もいるのではないでしょうか。そう,この評価関数はインパルス応答列に対して線形関数です。つまり,最小二乗法を適用することにより,インパルス応答例を評価関数の最適パラメータとして求めることができます。以上がインパルス応答推定に基づく制御対象のモデリング手法です。ここまでの手順は下記のようにまとめることできます。
1.初期実験データを取得。
2.データベクトルから構成される正方行列$A$を計算する。
3.初期出力データと正方行列$A$から最小二乗法にてインパルス応答を求める。
4.推定したインパルス応答列をFIRフィルタ$P_{m}$として導出する。
過学習抑制に向けた正則化最小二乗法適用
上記のアプローチを利用することでFIRフィルタのインパルス応答を推定できます。ただし、それは「初期実験データに含まれるノイズや外乱の影響が十分小さい」場合のみ限定されます。
システム同定に知見のある方であれば、過学習といった言葉を聞いたことがあるでしょう。FIRフィルタの次数は初期実験データのデータ点数となります。データ点数が1000点であれば、FIRフィルタの次数も1000点となってしまうのです。そのような高い次数の伝達関数のパラメータを最小二乗法で導出してしまうと、過学習によって汎化性が損なわれてしまいます。実験データにノイズが含まれていれば、本来再現すべきでないノイズの挙動も再現してしまい,望ましいモデルを得ることができなくなってしまいます。
そのような現象を回避する場合、通常の最小二乗法ではなく正則化最小二乗法を使います。色々な方法がありますが、もっとも簡単な手法がRidge回帰と呼ばれる回帰分析手法です。Ridge回帰では、通常の評価関数の代わりに下記の正則化項付きの評価関数
J_{p}(\rho)=J_{FIR}(\rho)+\lambda \sum_{i=0}^N p^{2}(i)
を最小化します。右辺の第二項がL2正則化項となっており、$\lambda$が正則化項の影響を決定する正則化係数です。この評価関数を最小化すると、本来の評価関数とインパルス応答列のL2ノルムの両方が小さくなるようなインパルス応答列が算出されます。言い換えると、インパルス応答列の中で本来の評価関数$J_{FIR}$の低減に寄与しない要素の値が小さくなります。本来再現すべきでないノイズの挙動も再現してしまうようなパラメータが計算されなくなるため、過学習を抑制できるのです。上記の評価関数の最適解は下記の式から掲載できます。
\rho^*=(A^TA+\lambda I)^{-1} A^T Y
以上がRidge回帰による最小二乗法です。ここまでの手順は下記のようにまとめることできます。
1.閉ループ実験データにて初期実験データを取得。
2.データベクトルから構成される正方行列$A$を計算する。
3.初期出力データと正方行列$A$から最小二乗法にてインパルス応答を$\rho^*=(A^TA+\lambda I)^{-1} A^T Y$と推定する。
4.推定したインパルス応答列をFIRフィルタ$P_{m}$として導出する。
Matlabによるデモ
それでは例題を通して,実際にシステム同定のデモをしてみましょう。簡単な例として次の対象に対するシステム同定問題を考えてみましょう。制御対象の伝達関数を
P=\frac{2}{(s+1)^{3}} e^{-0.15s}
と設定します。また,制御器を一般的なPID制御器:
C=K_{P}+\frac{K_{I}}{s}
としました。本例題では,PIDゲインの値は$K_{P}=1$,$K_{I}=0.25$と設定しました。今回は開ループ実験することができず,上記のPID制御器$C$を使った閉ループ実験でしか制御対象のデータを得ることができません。さらに、Fig.1のブロック線図で示したように、本制御系ではノイズ$d$がシステムに印加されています。以上の問題設定のもと,閉ループ応答データから制御対象$P$を同定することを目指しましょう。
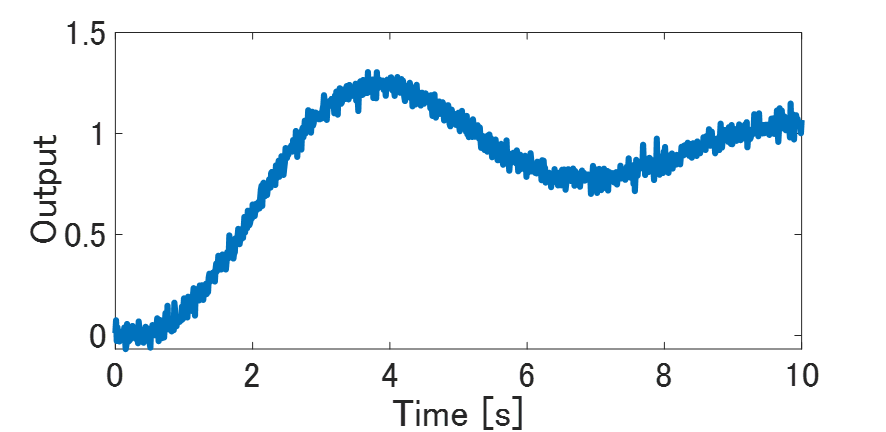
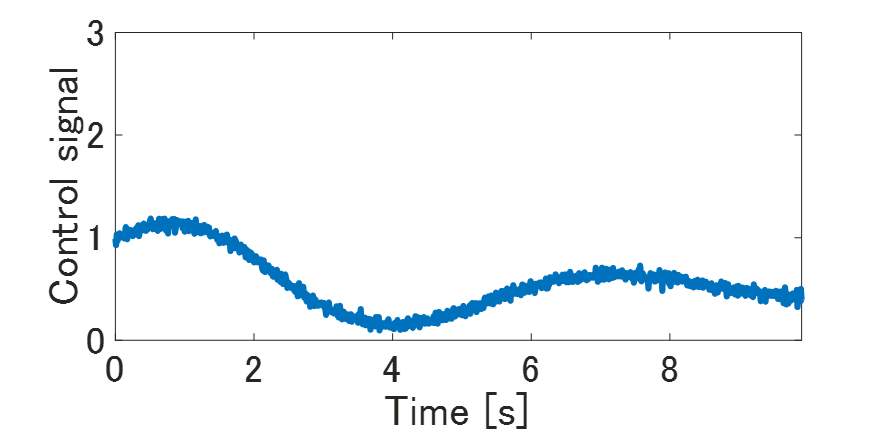
まず,閉ループ応答データを測定します。PID制御器を使った閉ループ実験にて,入出力応答を測定します。ここでは,$d$をホワイトノイズとして設定しました。Fig.2が実験時の閉ループ応答です。データ点数が$N=1000$となります。入出力データがノイズの影響を受けていることがわかります。このノイズまみれのデータを使って制御対象をモデリングしてみましょう。ここでは,Matlabのm-fileで作成したプログラムを用いてモデルを導出し,最小二乗法と正則化最小二乗法の二つの同定結果を比べてみます。正則化係数$λ$は$λ=1000$としておきました。
Fig.2 出力データ
Fig.3 入力データ
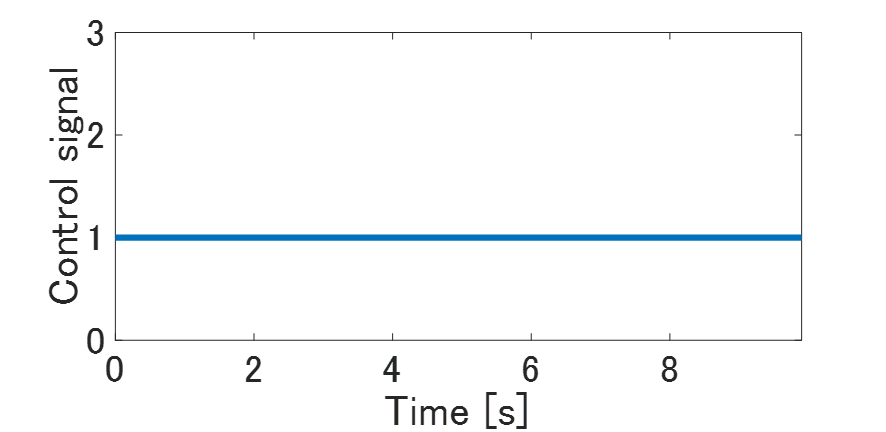
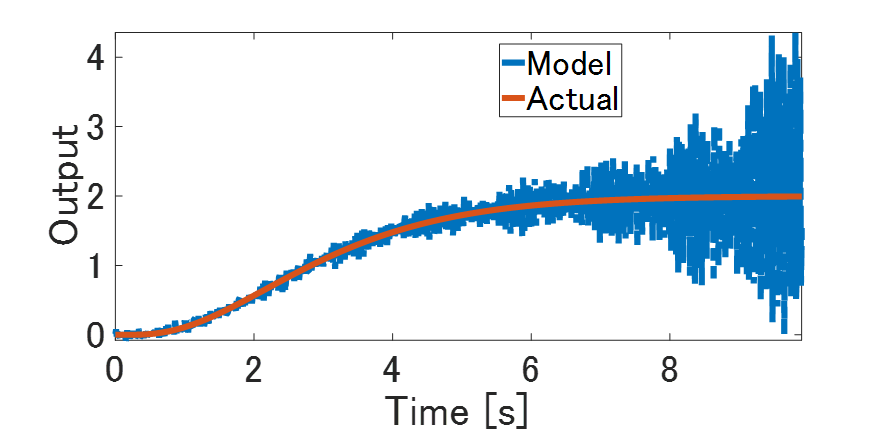
モデルの妥当性を確認するため,検証データとして振幅1のステップ入力を印加した開ループ応答と同定モデルの応答を比べてみます。まず、下記の結果が次数1000のFIRフィルタをデータから同定した結果です。残念ながら、同定モデルの応答と検証データの応答が乖離しています。やはり通常の最小二乗法では同定用データに対する過学習が生じてしまうようです。
Fig.4 テスト入力信号
Fig.5 テスト入力に対する応答(赤:真値、青:同定モデルの応答)
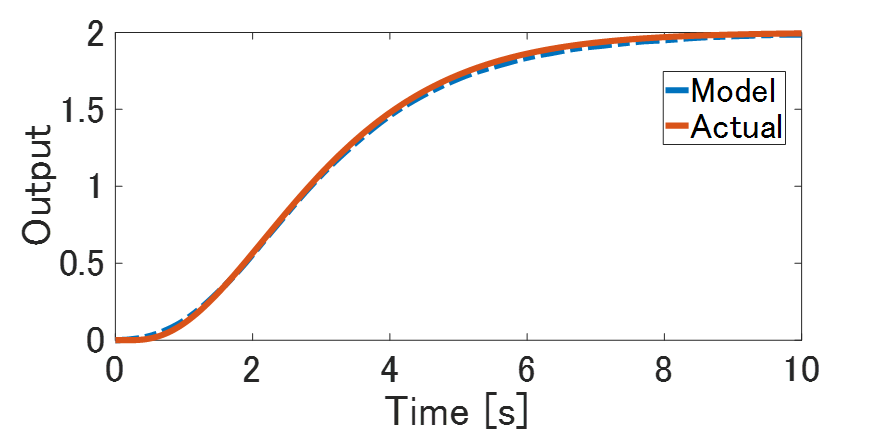
次に、正則化最小二乗法による同定モデルの妥当性を検証用を使って確認してみます。下記がモデルの応答と検証用データの比較結果です。こちらの結果では、モデルの応答と実験時の応答がおおむね一致しています。リッジ回帰による正則化によって過学習が抑制できていることがわかります。
Fig.6 テスト入力に対するFIRフィルタの応答(赤:真値、青:同定モデルの応答)
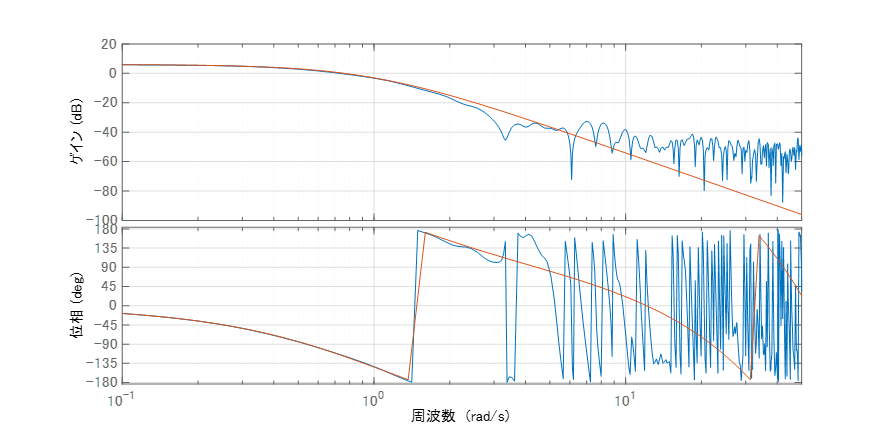
最後に、周波数特性の観点から同定モデルの妥当性を確認してみましょう。下記がリッジ回帰で同定したモデルと制御対象の周波数特性の比較結果です。正則化係数の調整が少し不十分なので高周波数帯域でやや乖離が生じていますが,制御対象のロールオフ特性とおおむね一致していることがわかります。以上の結果から,ノンパラメトリックなモデリングアプローチにて制御対象の数学モデルを得ることができました。
Fig.7 周波数応答(赤:真値、青:同定モデルの応答)
おわりに
今回は,未知システムのモデルを閉ループ実験データから簡単な手順で同定する方法について解説しました。ノイズが混じったデータを使っても,適切にモデル同定できることをご認識いただけたかと思います。本記事で解説した手法はあくまでモデリングアプローチの一つでしかなく,他にも有望な手法は多数提案されています。ただ,本記事の手法は制御対象の事前情報が余り得られない状況でも,ある程度高精度なモデリングを導出できるという利点があります。もしご興味あれば,皆様の業務・研究でも活用してみてください。
サンプルコード
Matlabで作ったサンプルコードを記載しておきます。このプログラムを使うと,最小二乗・Ridge回帰両方の手法でFIRフィルタを導出できます。
% yが出力の時系列データベクトル、uが出力の時系列データベクトル
nu=length(y);
A=ones(nu,length(y));
for i=1:nu
A(i,:)=lsim(tf([zeros(1,i-1) 1],1,0.01,'Variable','z^-1'),u,t);
end
A=A';
lambda = 1000;% 正則化係数
B=(A'*A+lambda*eye(nu))\A'*y;% リッジ回帰によるパラメータ算出
Bs = pinv(A)*y;% 最小二乗法によるパラメータ算出
% 最小二乗法によって導出したパラメータからFIRフィルタを算出
ttf=tf([0],1,0.01,'Variable','z^-1');
for i=1:nu
ttf=ttf+B(i)*tf([zeros(1,i-1) 1],1,0.01,'Variable','z^-1');
end
% リッジ回帰によって導出したパラメータからFIRフィルタを算出
ttf_FIR=tf([0],1,0.01,'Variable','z^-1');
for i=1:nu
ttf_FIR=ttf_FIR+Bs(i)*tf([zeros(1,i-1) 1],1,0.01,'Variable','z^-1');
end