機械学習と統計学、予測と因果など、これまでにもこうした違いについて何回か取り上げてきました。
実は言語学、自然言語の研究分野でもこうした違いに関しての論争があります。その中でも有名なのは、近代の言語学の父とも言われるノーム・チョムスキーと、AI分野の第一線の研究者でGoogleの研究部門のディレクターでもあるピーター・ノーヴィグの間でのものです。
そのことについて触れている「Predicting vs. Explaining」というおもしろい記事があったのでここで紹介します。
以下は一部の要約です。
チョムスキーは、言語というデータのなかにある法則性を説明することができないのであれば、それはサイエンスではないと主張します。
それに対して、ノーヴィグはそもそも言語とは説明できるほど単純なものではなく、逆にその複雑性を受け入れたモデルを作ったからこそ、近年の自然言語の分野で見られる飛躍的なイノベーションが可能になったのだと主張します。
確かに近年の言語認識、言語翻訳などの分野は、データとアルゴリズムを使って人間には解釈が不可能なモデルを作ることで飛躍的に発展してきました。
チョムスキーは、サイエンスがいつも果たそうとしてきた目的とは「理解する」ということで、「予測する」というのは、現在何が起きているのかに対するだいたいの推測に過ぎず、それでは物事の本質的な理解にはつながらないと言います。
つまり、サイエンスの目的とはシステムの仕組みを説明するための原則を発見することにこそあり、そのための正しいアプローチとはデータに勝手にドライブさせるのではなく、逆に理論によってデータを案内していくべきだと主張します。
注意深くデザインされた実験を通して関係のない余計なものを取り除いていくことでシステムの本質を学んでいくべきであり、これはガリレオ・ガリレイ以来のモダンサイエンスが歩んできた道なのだと言います。
「分析されることもないカオスのようなデータを処理しようとするだけでは、どこにもたどり着かない。そんなやり方ではガリレオでさえどこにもたどり着くことはなかっただろう。」
と、チョムスキーは言います。
しかし、そもそもこうした対立というのは、Leo Breimanによって書かれた"Statistical Modeling: The Two Cultures”の中で出てきた「2つの文化」の違いによるものではないでしょうか。
訳者注:ちなみにこのLeo Breimanはランダムフォレストの父とも言うべき人です。
その文化とは、「データモデリング文化」と「アルゴリズム文化」のことです。
データモデリング文化
自然というのはブラックボックスで、変数間の関係は確率的に捉えられるので、モデリングをする人の仕事はこうした前提となる関係性と最も合うモデルを見つけ出すこととなります。
アルゴリズム文化
ブラックボックスの中の関係性はそもそもシンプルなモデルで表現するには複雑すぎるので、モデリングをする人の仕事は、その中の変数間のほんとうの関係性というものを気にすることなしに、アルゴリズムを使ってインプットとなる変数からいかに最もよいアウトプットを推測できるかということになります。
ノーヴィグやBreimanは後者の「アルゴリズム文化」に属します。彼らは、言語のようなシステムは複雑すぎて、ランダムすぎて、さらに偶発的すぎるので、人間が理解できるほどの数のパラメーターを使って表現できるわけがないと主張します。
シンプルなモデルを作るというのは、現実世界からかけ離れたおとぎの世界に何らかのものを作り出そうとしているようなもので、それでは言語というものが何なのか、どう機能するのかという重要なことから離れていってしまうと主張します。
「私達のゴールは極端に素晴らしい理論を作ることにあるのだというふりはもう辞めるべきだ。代わりに、複雑性を尊重し、最も使いやすい味方、つまりこうしたことに効果的に使えるデータを使うべきなのだ。」
しかしどちらのグループにしろ、彼らは一つの点では同じ意見を持っています。それは大量のデータを機械学習のアルゴリズムにかけることで、それぞれの変数を全く理解しなくとも、よりよい予測結果を出すことができるという事実です。
予測能力と説明能力はよく混同されてしまいます。高い説明能力を持つモデルは高い予測能力を持つと仮定されます。
しかし、最高の予測能力を持つモデルを作るためのアプローチは、最高の説明能力を持つモデルを作るためのアプローチとは全く違うものなのです。モデルを作っていくときの決定はこの2つの異なるゴールの間でのトレードオフとなります。
柔軟性と説明性
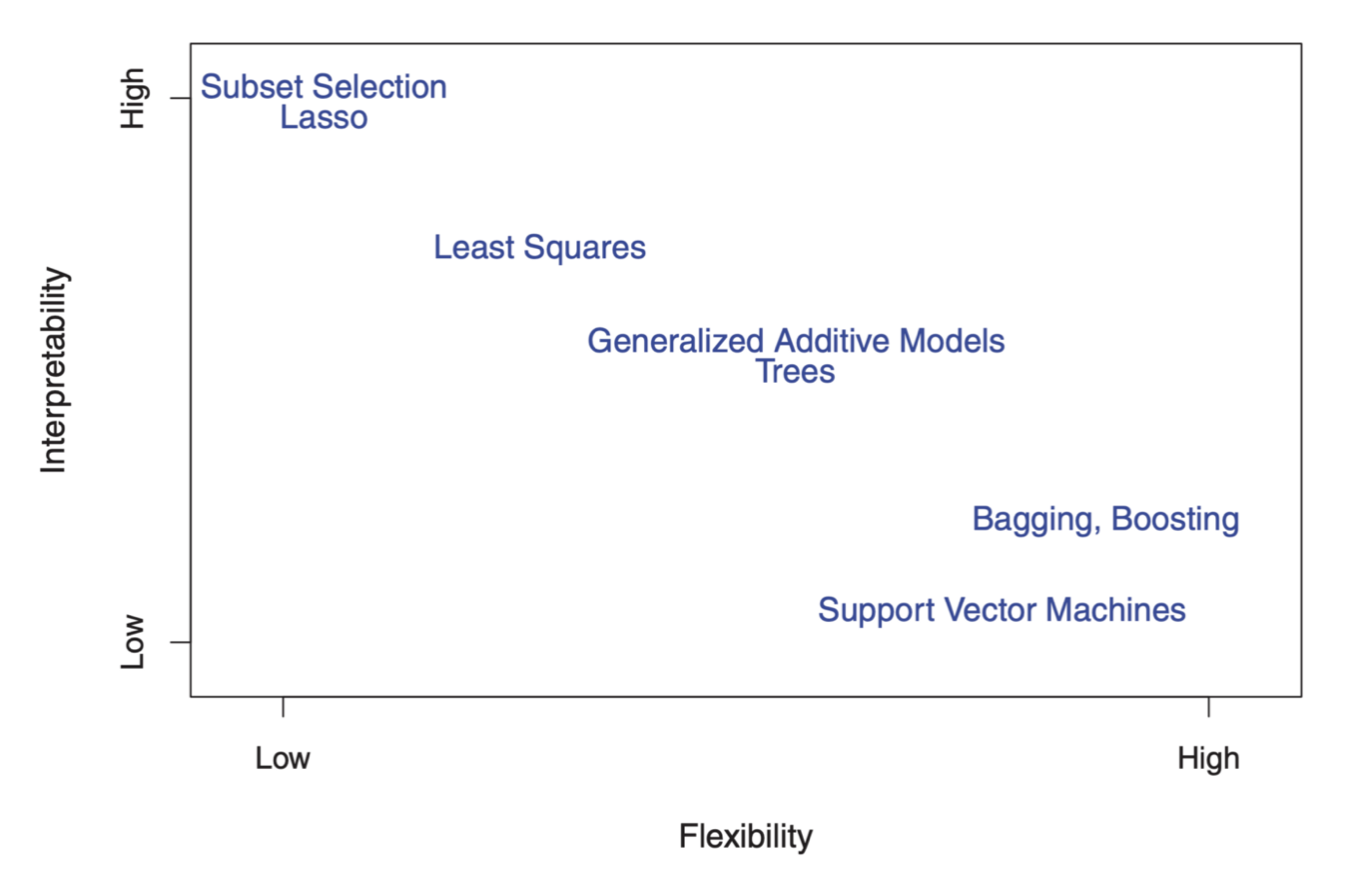
線形回帰やロジスティック回帰といった統計のモデルはもととなるデータへの仮定や制限が多く、さらに単調なパターンを捉えるというのが前提です。
それに対して特に機械学習系のモデルはあまり制限がなく、さらに単調でないパターンも捉えることができます。その点で、機械学習のモデルは柔軟で、逆に統計のモデルはあまり柔軟ではありません。
そうすると、現実世界のデータというのは、単調でないことが多いので、より柔軟性を持ったモデルのほうがデータにフィットしやすいということになり、そのことが予測精度を上げることになるのです。
しかしより柔軟性のあるモデルというのは一般的にはより複雑であり、より多くのパラメーターの調整を必要とし、さらにはデータの中にある変数がどのように結果に影響しているのかを理解するには複雑すぎるようになります。
それに対して、線形回帰のようなモデルは、予測精度という点からはいまいちかもしれませんが、それでもシンプルで人間にとっては解釈しやすいものなのです。
因果関係の発見と反事実的推論
因果推論は統計モデルのみによって行われることはありません。というのも、実はドメイン知識を必要とするからです。
変数同士の関係性に関する理論的な理解をもとに、推測された因果を正当化させる必要があるのです。それゆえ因果推論のためのデータ分析や統計モデルは理論的なモデルによって大きく導かれていくものなのです。
映画業界の例
映画スタジオは予測モデルを使って興行収入を予測することで、映画の金融的な成功(または失敗)がどうなるかを予想し、彼らの映画のポートフォリオのリスクとリターンを評価します。
しかしこうした予測モデルは映画市場の仕組みやダイナミクスを理解し、投資の判断をするための情報を提供するという観点からはあまり使い物になりません。
なぜなら、投資の判断が必要となる映画の制作の最初のステージでは、起きうるであろう結果の幅があまりにも大きく振れるため、最初のステージで手に入るようなデータを元にして作られる予測モデルの正確さは大きく損なわれます。
予測モデルの性能は、リリースが迫ってきたときにもっともよくなりますが、それまでには制作に関するたいていの意思決定はすでに終わっています。つまりこのことは、予測をしてもその結果をもとに特に起こせるアクションが何もないということを意味するのです。
それに対して、因果推論のモデルは、制作の初期段階であっても、制作に関する属性の違いがどのように結果に違いを与えるのかをスタジオの意思決定者が考慮するために役立ちます。こうした情報というのは制作に関する戦略を作るときには特に重要なものなのです。
以上、要訳終わり。
あとがき
最初の方にあった、チョムスキーとノーヴィグの両者の主張はどちらも理にかなっているような気がします。
サイエンスの目的とは、自然現象の説明、予測、そしてコントロールだと思いますが、その最初の一歩である説明ができないのであれば、失敗を繰り返しながら時を経て進化していくことができないのではないか、最適化はできるけど、もっと大きなブレイクスルーにつながらないのではないか、と思ってしまいます。
しかし、ノーヴィグが主張するように、この世の中は複雑なものなので、それを簡単に説明しようとした途端に現実からは離れていったものになってしまうというのも確かです。
しかしそれでも、そうした複雑な世界であるにも関わらず、最終的には「シンプル」な原則や計算式を導き出したことでサイエンスの世界での大きなブレイクスルーにつながり、その結果の上に特にこの400年ほどでの私達人類の急速な進化が可能であったというのも事実です。
こうした対立軸がある時というのは、どちらが正しく、どちらが間違っているというのではなく、どちらも正しく、どちらも間違っていると受け入れるほうがいいのではないかと思います。(ちょっと禅問答のようになってしまいますが。。。)
そこで、私達データ分析に関わるものは、統計も機械学習のどちらも普段から慣れておいて、いざとなったらいつでも使えるように自分の道具箱に入れておいて、場合によって使いやすいものを使いやすい組み合わせで使っていくのがいいのではないでしょうか。
結局、特にビジネス上のデータ分析に関わるものとしては、目的は分析の手法やツールの正しさの追求にあるのではなく、自分たちのビジネスの改善、または問題の解決にあるのです。そして、そこには完璧な答えなどというものはないのです。
そして、この答えがないというところがデータサイエンスの最も面白いところではないでしょうか。
データサイエンス・ブートキャンプ、11月開催!
次回のデータサイエンス・ブートキャンプは11月です!
ビジネスを成長させるためにはデータを使って因果関係に関する仮説を構築し、実験するというサイクルを効率的に回していく必要があります。そしてそのためには統計、機械学習を含むデータサイエンスの手法を習得する必要があります。
「データ・インフォームド」な意思決定を行いたい方、データサイエンスを1から体系的に学びたいという方はぜひ参加してみてください。
詳細はこちらのページにあります。