みなさん、「情報カスケード」という言葉、聞いたことありますか?
これは、みんな個人的には何かがおかしいと思っているにも関わらず、自分の属する集団が「正しい」と思っていることをいつまでも「正しい」と思い込んでしまうことになる仕組みのことです。
カスケードとは階段になっている滝のことで、直訳すると情報が上の方からどんどんと勢いを増して広まっていくということになります。問題はその情報が間違ったものだったとしても、それらはどんどんと広がっていくだけでなく、一度勢いをつけると止めるのが難しく、さらに、一度この情報カスケードによって作り上げられた世界に入ってしまうと、まるで「無限ループ」のようにそこからなかなか抜け出すことができなくなってしまうのです。その結果、一度出来上がってしまうと、いつまで経ってもその「間違い」を集団で信じ続けてしまうという、厄介な仕組みです。
こういう話をすると、「デマを信じる頭の悪い人達の話」、「陰謀論を信じる怪しい人達の話」と他人事のように思うかもしれませんが、実はこの仕組みは頭が悪い良い関係なく、誰でも簡単に飲み込まれてしまうものなのです。
それでは、この厄介な「情報カスケード」がどう出来上がるのか、そしてどう打ち破るのかについて、以下の資料を元に解説してみたいと思います。
- Networks, Crowds, and Markets: Reasoning about a Highly Connected World - Link
プライベート情報とパブリック情報
普段私達は様々な場面で意思決定を行いますね。
例えば、会社で新しいテクノロジーを採用するかどうか決める、新しいスタイルの服を買うかどうか決める、新しいレストランに行くかどうか決める、原発反対、賛成などある特定の政治的な立場を支持するかどうか決める、などです。
それでは、私達は一般的にどのように意思決定するのでしょうか?
理想的には、その対象について自分で独自に調査し、実際に自分の手で使ったり食べたりし、さらに他の様々な専門家から意見を聞き、それらを元に自分で最適だと思う答えを導き出せればいいのですが、実際にはそんなことはしませんね。
私達は毎日忙しく、さらにそうした決定を一日の間にいくつも行わなければいけませんし、さらにそうした決定を素早く行わなければ目の前にあるチャンスを見逃してしまう、なんてこともあります。
そこで、実際には他の人がすでに下した決定を参考にすることになります。あるレストランに行くかどうか決めたいのであれば、すでにそこに行って食事をした人の意見を聞いたり、オンラインでそうした人達のレビュー評価を見て決める、といったようにです。
実際にレストランに行った人はそこで料理を食べ、店員と話し、店の雰囲気を体感したわけですから、1次情報を持っています。これはその人にしかわからない情報なので、その人にとっての「プライベート」な情報と呼びましょう。
これとは別に、実際にレストランに行った人がオンラインなどでそのレストランを評価すると、その評価情報は他の人にも共有される情報となります。これを「パブリック」な情報と呼びましょう。これは例えある会員限定の空間でしか共有されていなかったとしても、1次情報を持っている人以外に広まった情報ということで「パブリック」情報と呼びます。
さて、あなたがこの「パブリック」情報を手にしたとき、意識するしないに関わらずこの「パブリック」情報を発信した人が得た1次情報、つまり「プライベート」情報を推測することになります。
その人がその店で食べたパスタがおいしいと行った場合、「おいしい」という感覚はあなたは直接体験したわけではないのでわかりませんが、それはあなたのいう「おいしい」という意味と同じだろうとか、またはこの人は何でもおいしいというので、そこまで特別においしいという意味ではないだろうなどと、推測するわけです。
つまり、あなたはその人が共有した「パブリック」情報を元にその人の「プライベート」情報を推測したことになります。あなたには、彼の「プライベート」情報を正確に知ることはできません。ただ推測することしかできないのです。これが「情報カスケード」を理解するための重要なキーとなります。
私達は多くの場合「パブリック」情報を元に「プライベート」情報を推測し、そこに可能であれば自分だけのもつ「プライベート」情報を加味し、意思決定を行っています。
そしてこのことが、集団の中での意思決定にとって大惨事となることがあります。
情報カスケードの実験
ここで、これまで話してきた「パブリック」情報を使って意思決定をすることに潜む問題を解説するために、Lisa R. Anderson と Charles A. Holtによって昔行われた実験の話をします。(リンク)
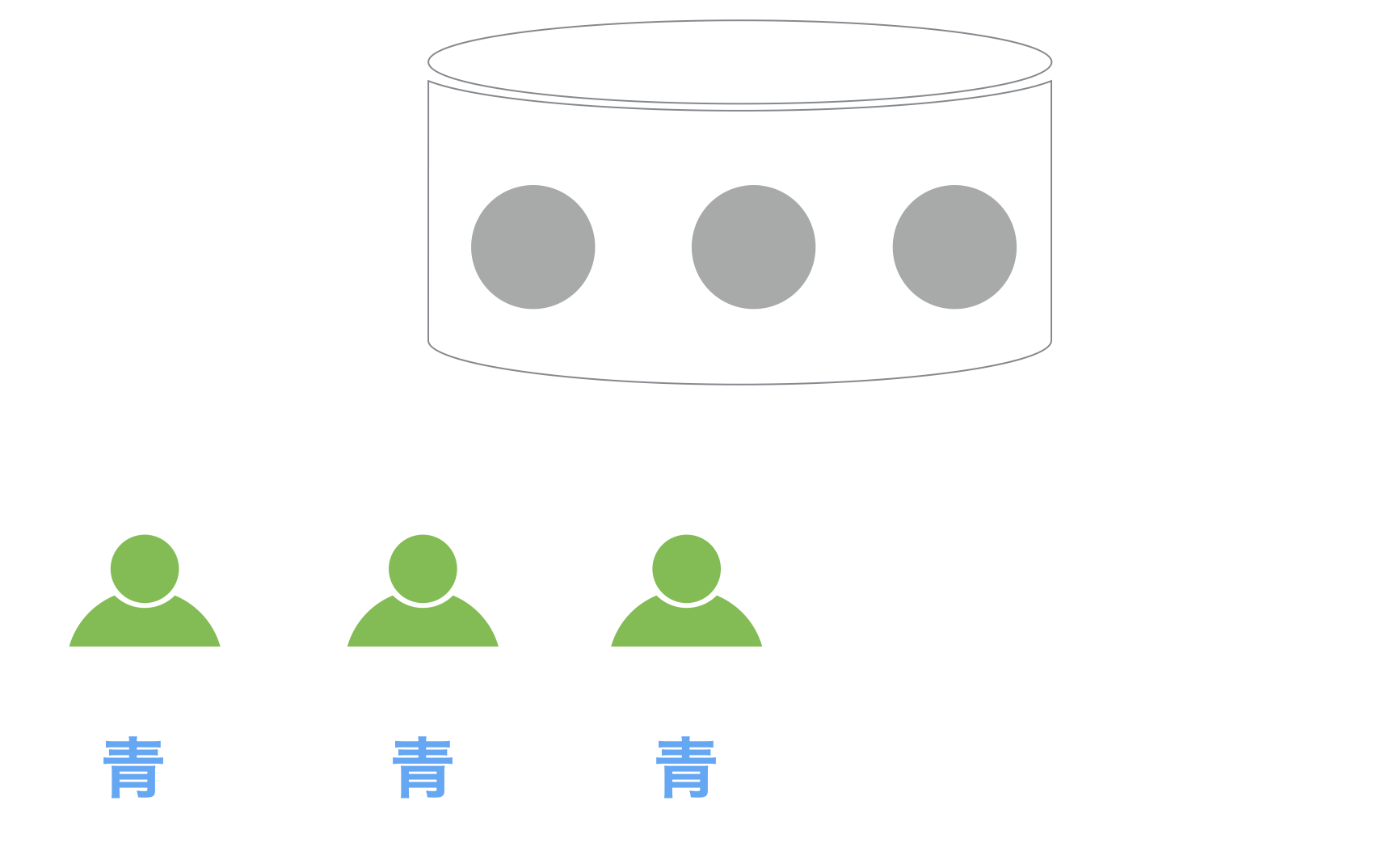
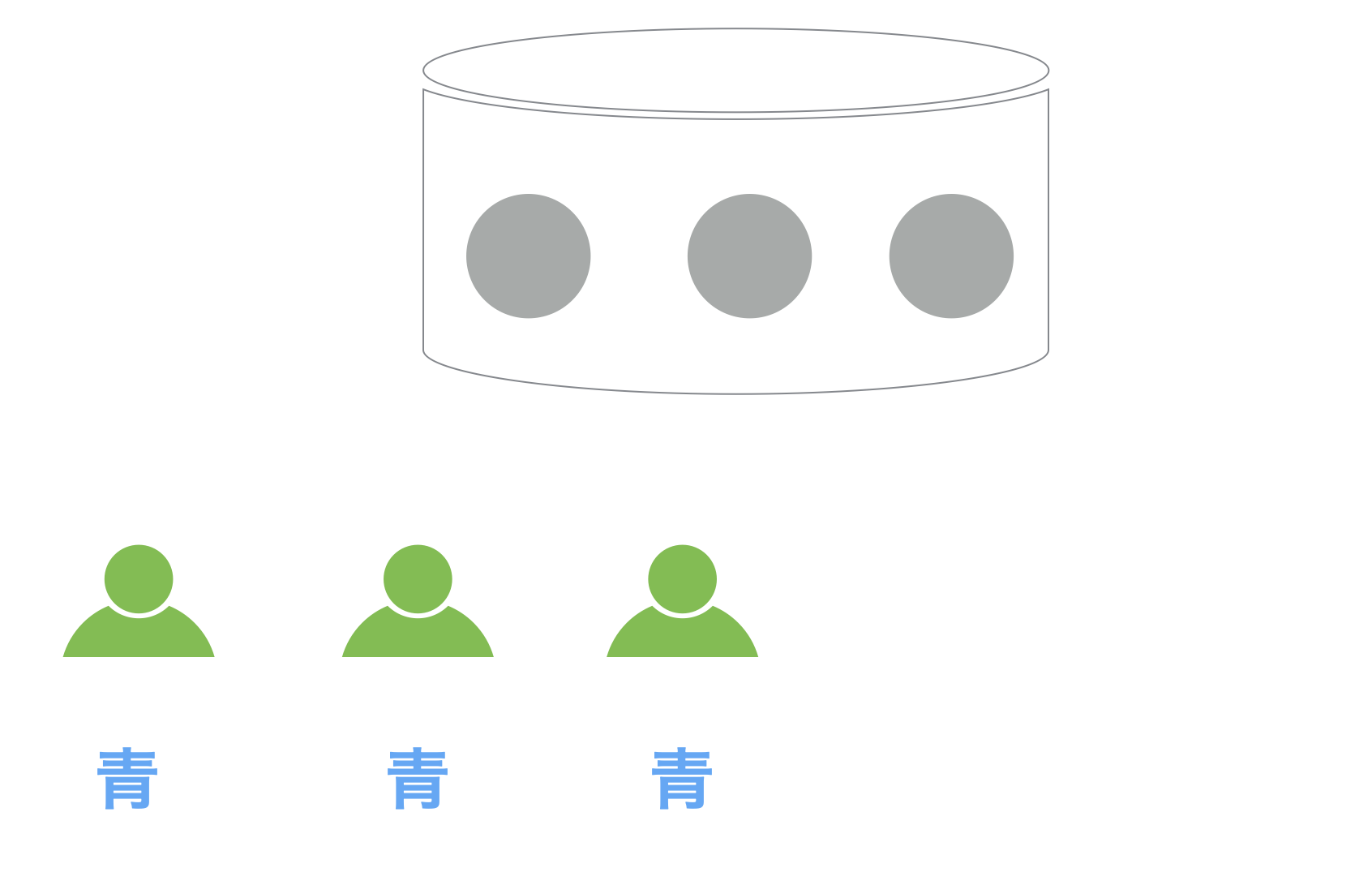
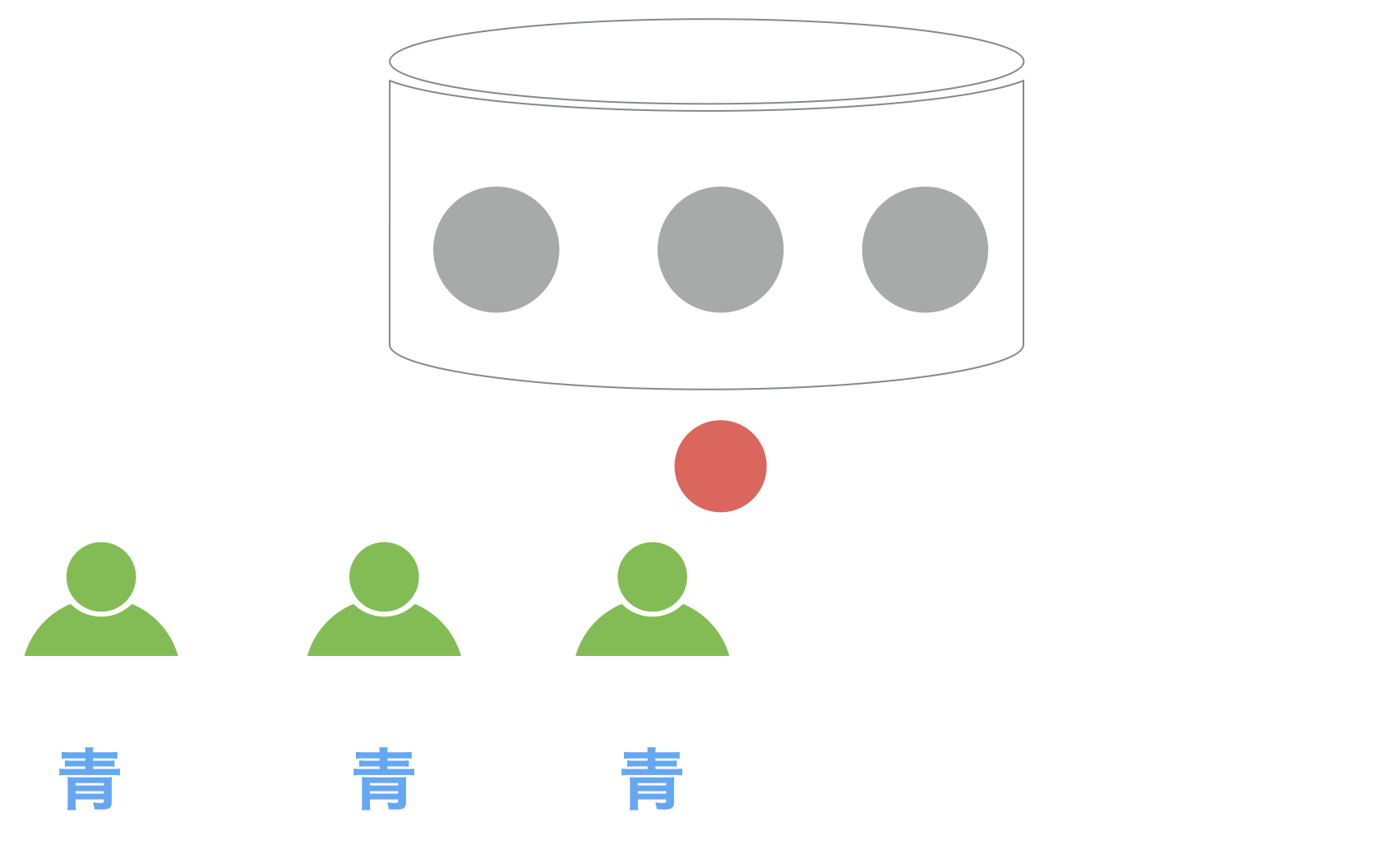
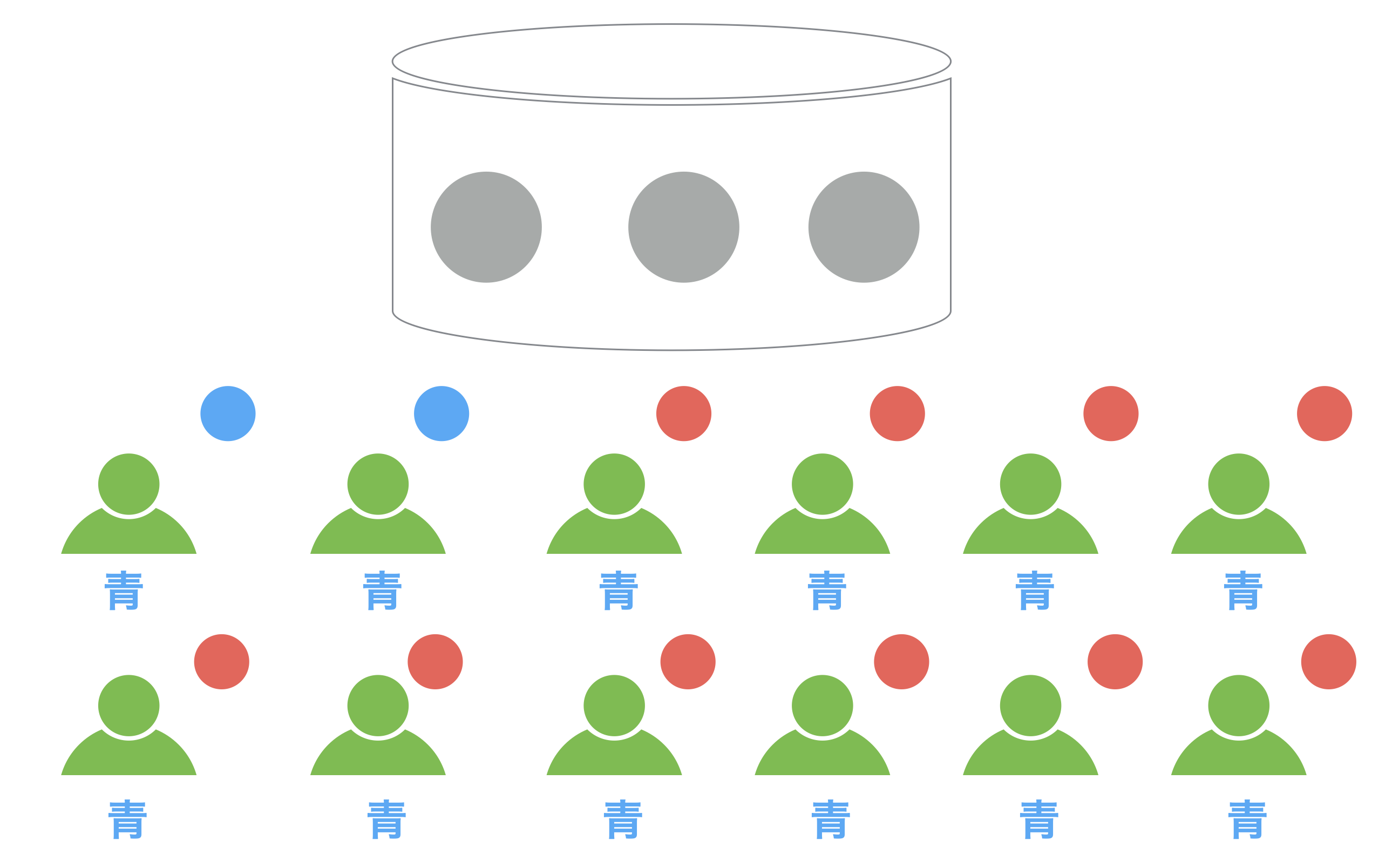
まず、ある容器の中に赤と青の3つのボールがあります。この容器は外からは中身が見えないようになっていて、赤が多いのか青が多いのかは参加してもらった人達には知らされていません。
100人の人達に集まってもらい、この容器の中のボールは赤か青のどちらが多数派かを当ててもらいます。赤が2つ入っていれば「赤が多数派」、青が2つ入っていれば「青が多数派」ということになります。
これを一度にみんなに答えてもらうのではなく、順番に行っていきます。
1人ずつ前に来てもらって、容器の中から他の人には見えないように1つだけボールを取り出し、色を確認した後ボールを容器に戻したあとで、容器の中は赤と青のどちらが多数派であるかを推測し、部屋にいる他の人達に発表してもらいます。
それでは、具体的に見ていってみましょう。
まずは最初の1人目です。
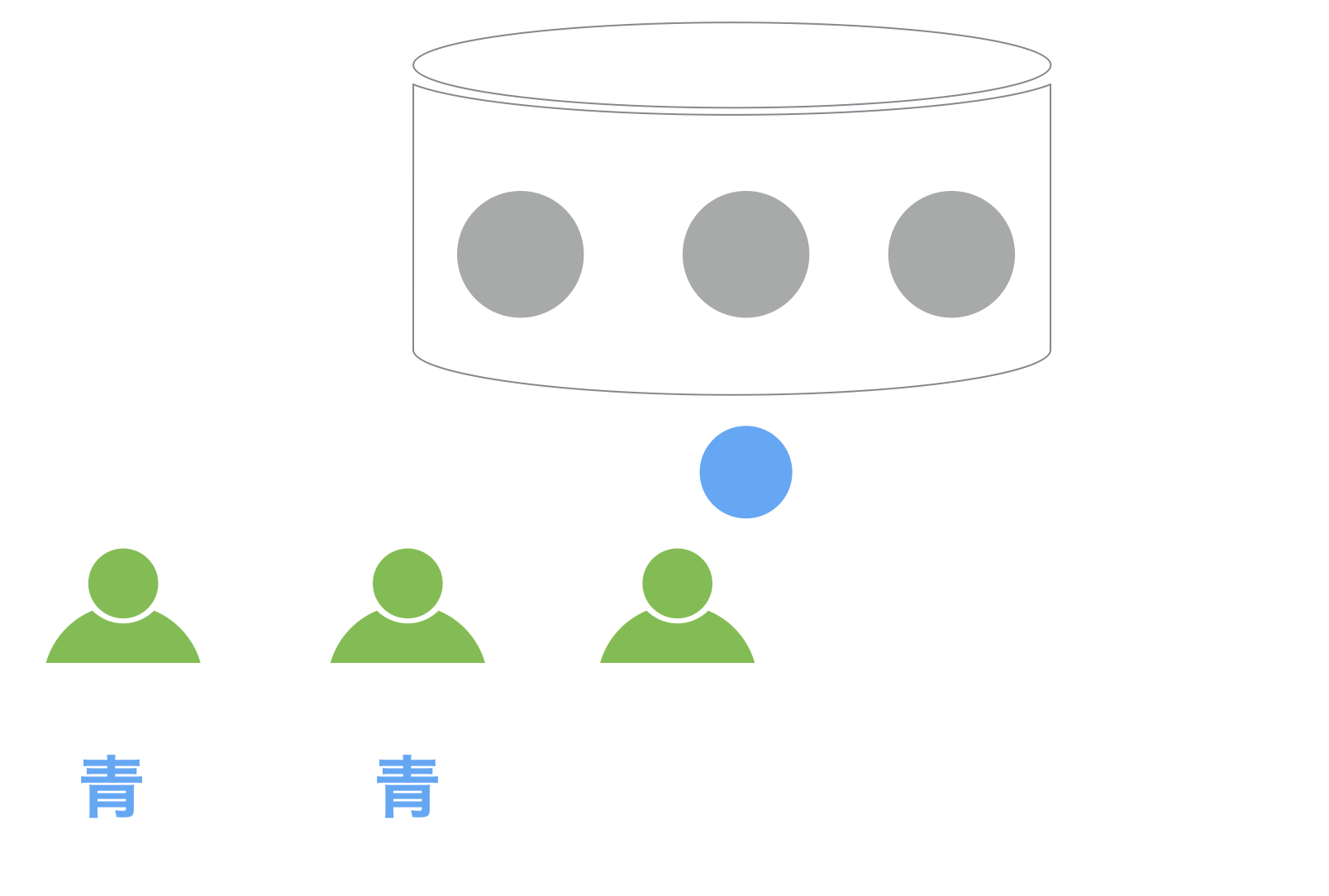
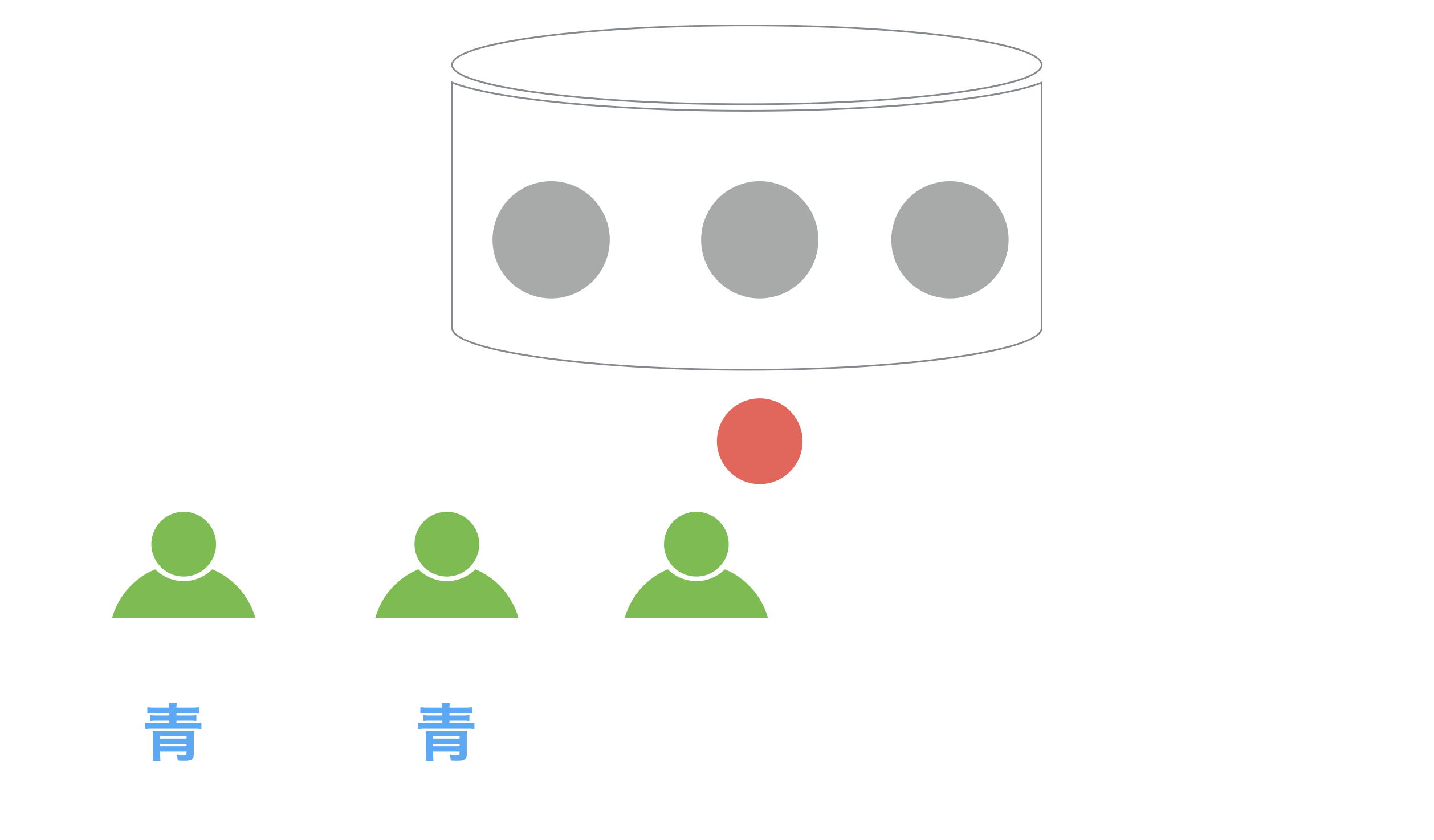
この人は青いボールを取り出しました。このボールを誰にも見られないように元の容器に戻した後、彼は青と赤のどちらが多数派だと意思決定するでしょうか?
これは確率論を使って数学的に証明することもできるのですが、この場合直感的に正しいと思う答えが最適な答えとなります。それは「青が多数派」ということです。(確率論による証明に興味のある方は元の論文を見てみてください。)
そしてこの実験ではみんなに自分が最適だと思う答えを正直に発表してもらうことになっているので、この人は「青が多数派」だと発表しました。
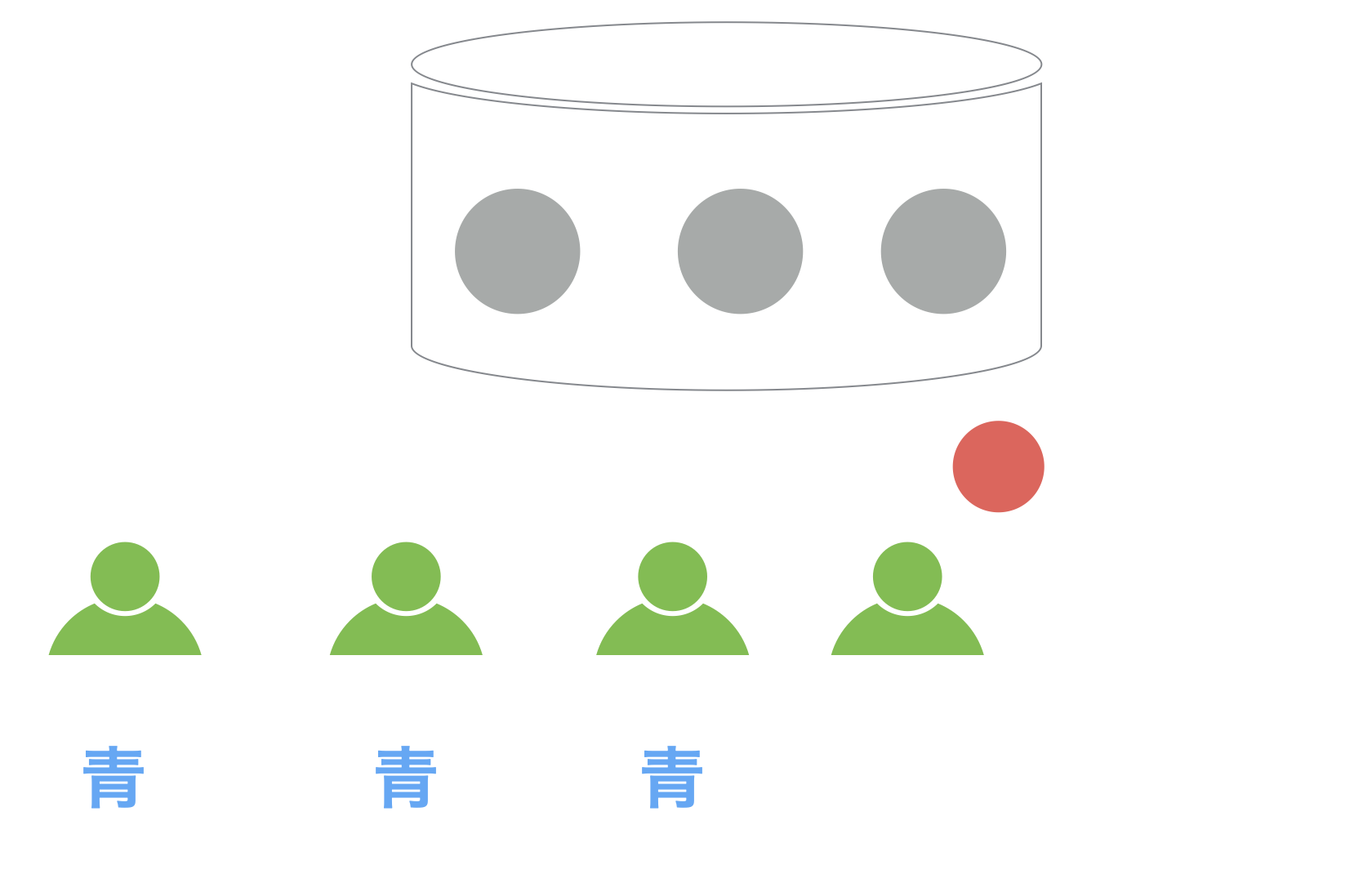
次に2人目に前に来てもらい、同じように容器からボールを他の人には見えないように取り出して色を確認してもらうと、青が出ました。
このとき、彼は青と赤のどちらが多数派だと発表するでしょうか?
このとき、この2人目は2つの「情報」を使って意思決定することになります。まずは、1人目が「青」と発表した「パブリック」情報です。この情報を元に1回目は「青」が実際に出たんだろうと推測します。次に、自分にだけ分かっている2回目に「青」が出たという「プライベート」情報です。
この2つの情報より、つまり2回「青が出た」という情報を元にこの容器からは青が出やすいと推測すると「青が多数派」が最適な答えとなります。
そこで2人目は「青が多数派」だと発表することになりました。
もちろん、ここで2人目に赤が出ることも考えられますが、その場合はタイとなるので、今回のように意思決定は単純ではありません。それでもこの後何人かにボールを取り出してもらうことを繰り返すと次第に同じような状況、つまりどちらかが多数派と判断しやすい状況になっていきます。
今回は重要な点にポイントに絞って話を続けたいので、たまたま最初の2人に青が出たと考えましょう。
もう一度確認しておきます。現在のところ2人の人が容器からボールを取り出し、2人とも「青が多数派だ」と発表しています。
それでは、次は3人目です。
この3人目にも同じくまた青が出ました。
この場合は、もうすでにあえて説明するまでもありませんね。この人は自信を持って「青が出た」と発表することでしょう。
さてここで問題です。
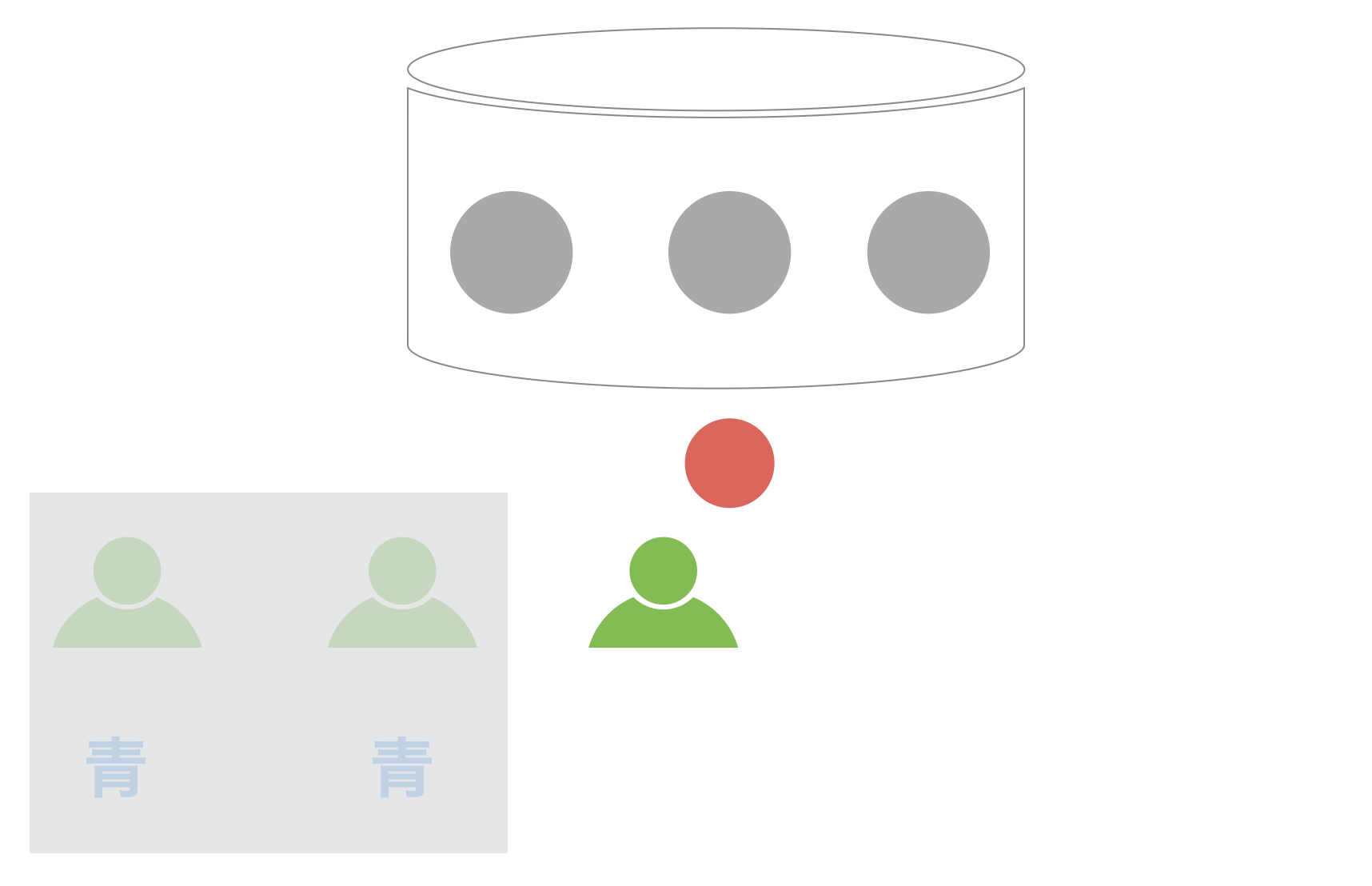
もし、この3人目に「青」でなく「赤」が出ていたならばどうでしょうか?
この人は「赤が多数派」と発表するでしょうか?それとも、「青が多数派」と発表するでしょうか?
確率的にはこの場合の最適な答えは、「青」となります。
というのも、もしすでに発表した前の2人の決定を正直で最適だと考えるのであれば、この時点では3回引いて2回青、1回赤が出たと推測することになります。そこで、確率的には青が多数派だと答えるほうが論理的で最適となります。
ところがここで思い出してほしいのは、この3人目の人はその前の2人の「プライベート」な情報は「わからない」のです。持っている情報は、自分の「プライベート」な情報と自分の前の2人の「パブリック」な情報です。
それでは、この3人目の人が前の2人の「パブリック」な情報をもっていなかった場合どうなるでしょうか?この場合、この人の中では彼が一番最初に容器からボールを取り出したのと同じということになります。
その場合、この人は「赤が出た」という情報のみによって判断しなければならないわけですから、この時点での確率的に最適な答えは「赤が多数派」と言うことになり、他の人達にそう発表するでしょう。
ところが、今回は彼の前の2人が「青が多数派」だとすでに発表してしまっていたので、彼は自分が見たものは赤であったのにも関わらず、「青が多数派」だと発表してしまうことになってしまったのです。
こうして「情報カスケード」の無限ループが始まります。
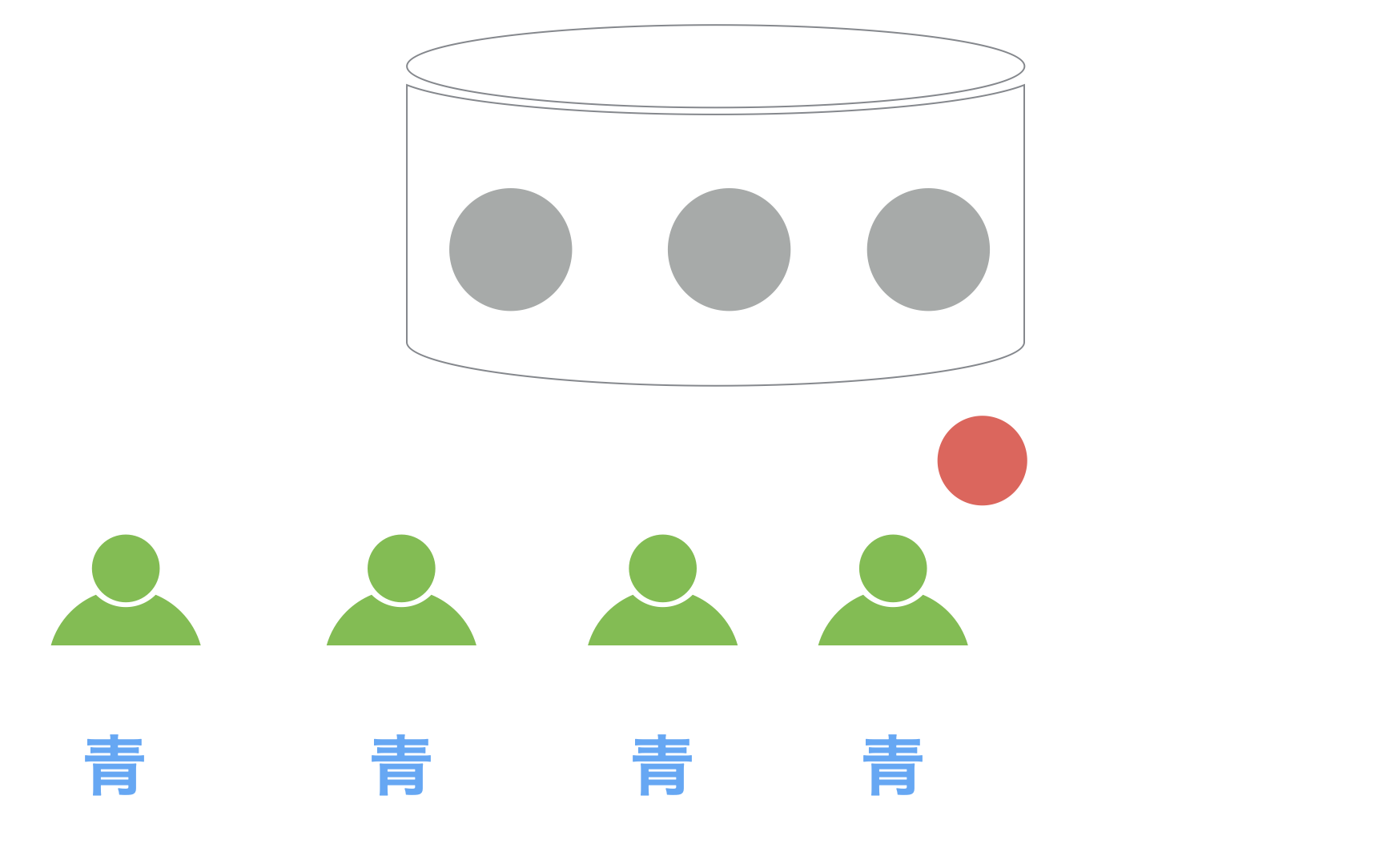
4人目を見てみましょう。
この人が容器からボールを取り出すと赤でした。
しかし3人目と同じように、この4人目の人も「青が多数派」だと発表することになります。というのも、すでに前の3人が「青が多数派」と発表しているので、あたかもすでに3回青が出ているのだろうと推測します。自分が引いた赤の1と合わせると、4回中3回青が出たのだから、青のほうが出やすいと考え、それなら容器の中は「青が多数派」だろうと考えるのは論理的であり、確率論的にも最適であります。
この後はもういちいち見るまでもありません。自分に青が出ればもちろん「青が多数派」だと発表するでしょうし、赤が出たとしても、4人目の論理と同じで「青が多数派」だと発表することになります。
そして、人数が増えれば増えるほど、例え自分の「プライベート」情報が「赤が出た」だったとしても、それまでの圧倒的なまでの「青が多数派」という「パブリック」情報によって、自分の「プライベート」情報を元に意思決定できなくなってしまうのです。
よく考えるとこれはおかしなことです。というのも実際には他の人達の「青が多数派」というのは「パブリック」情報で、ほんとうはどうだったのかという「プライベート」情報ではないわけです。
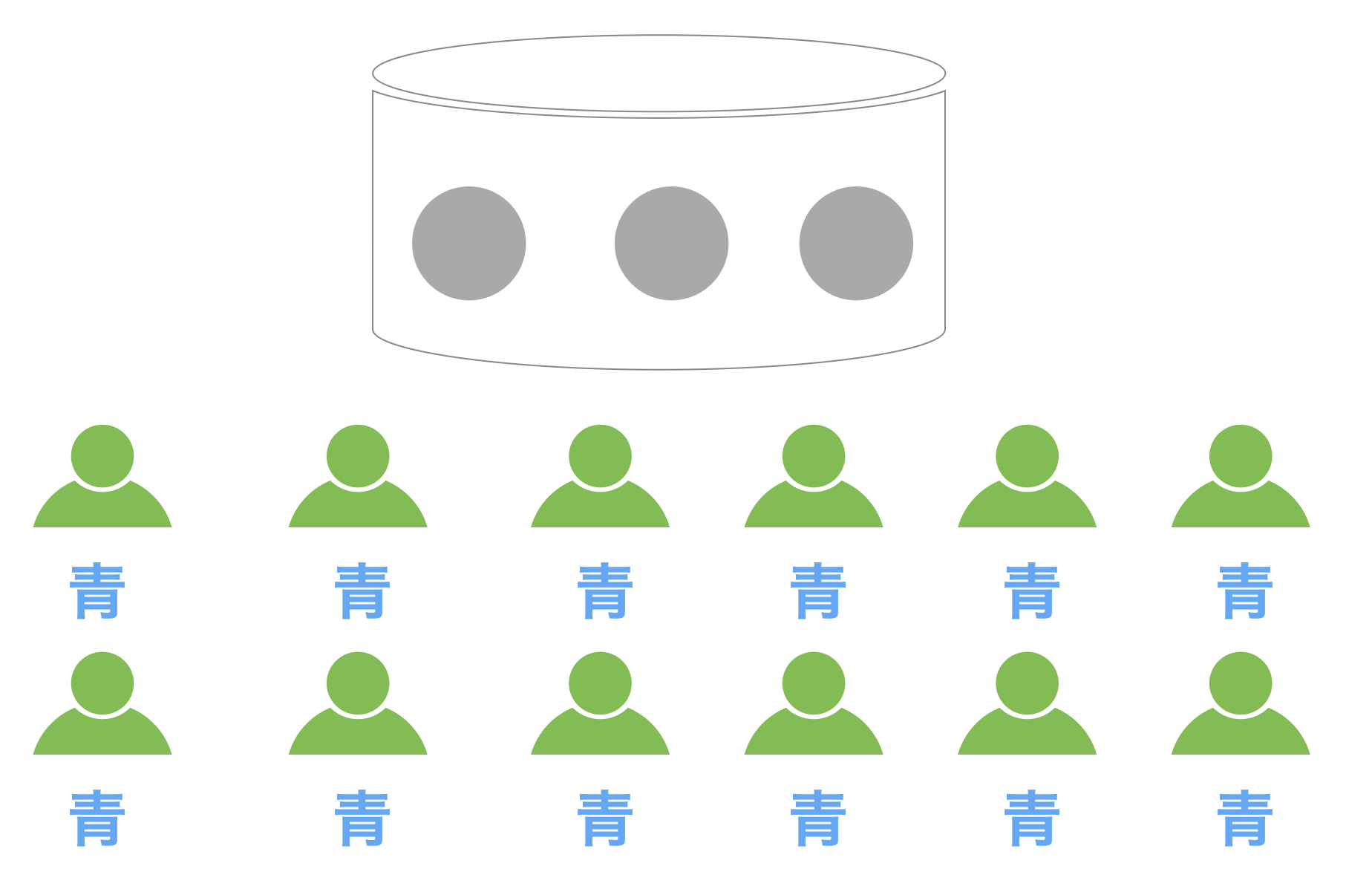
21人目の人がいて、仮にその人の前の20人中最初の2人を除く18人には全て赤が出ていたとしても、それは「プライベート」情報であって「パブリック」情報ではないため、この人から見るとほとんどの人に青が出たんだろういうことになり、「青が多数派」と推測するしかないのです。
こうして、実は容器の中は「赤が多数派」だった場合でも、もし、最初の2人が「青が多数派」だと発表してしまうと、この実験に参加した100人はみんなで間違ってしまうということになってしまうのです。
この結果だけを見ると、3人目以降の人は何も考えずにそれまでの人が下した決定をただ単に従っていくだけの、まるで羊飼いに飼いならされた自分で考えることができない羊であるかのようです。
しかし、ほんとにそうでしょうか?
簡単な情報操作
実は、それぞれの人はその時点その時点で利用可能な情報と確率論(数学)を使って最適な意思決定をしているのです。ある意味、スマートな意思決定を行ったとも言えます。
これが「情報カスケード(連続滝)」の1つ目の重要なポイントです。
つまり、みんなが論理的に最適な意思決定を下したにも関わらず、みんなで間違ってしまうことがあるということです。
さらにこうした状況は簡単に作れるのです。というのも今回はみんなに正直に答えてもらうという前提でしたが、現実世界でこのような状況があたっとき、最初の2人をコントロールすることができれば、その後の人達の答えを簡単に操ることができるということです。
確率論的なパラドックス
次に2つ目のポイントは確率論的なパラドックスです。
もし多数派が赤だった場合を考えてみましょう。
その場合、1人目が青である確率は1/3 (約33%)です。さらにその次の2人目も青である確率は、
1/3 x 1/3 = 1/9
となるので、1/9(約11%)となります。
つまり、こんなに低い確率でしか起こらないことでも、最初の2人が「青が多数派」だと発表してしまうことによって、その後何人も容器からボールを取り出し、そのうちの多くの人が赤を見たとしても、「赤が多数派」だという本来の正確な答えに近づくことができなくなってしまうのです。
これは確率論の世界でよく言われる、「データ量(今回の場合は参加者の数)が増えれば本来の答え、つまり確率論的に得られる答えに近づいていく」といういわゆる「大数の法則」とは相容れないものです。
すでに見たように、どんなに参加者の数が大きくなったとしても、最初の2人が青だと「間違って」意思決定してしまうと、そうした「パブリック」情報を持った後続の人達が「論理的に正しい」意思決定を行っている限り、いつまでたってもみんな間違い続けるだけでなく、間違いから余計に抜け出しにくくなってしまうのです。
無限ループを打ち破る方法
ところが、ここでいいニュースがあります。
一度はまると2度と抜け出すことができない「無限ループ」のように見えるこの仕掛け、実は打ち破る方法があるんです。
それが、この「情報カスケード」における最後の重要なポイントです。
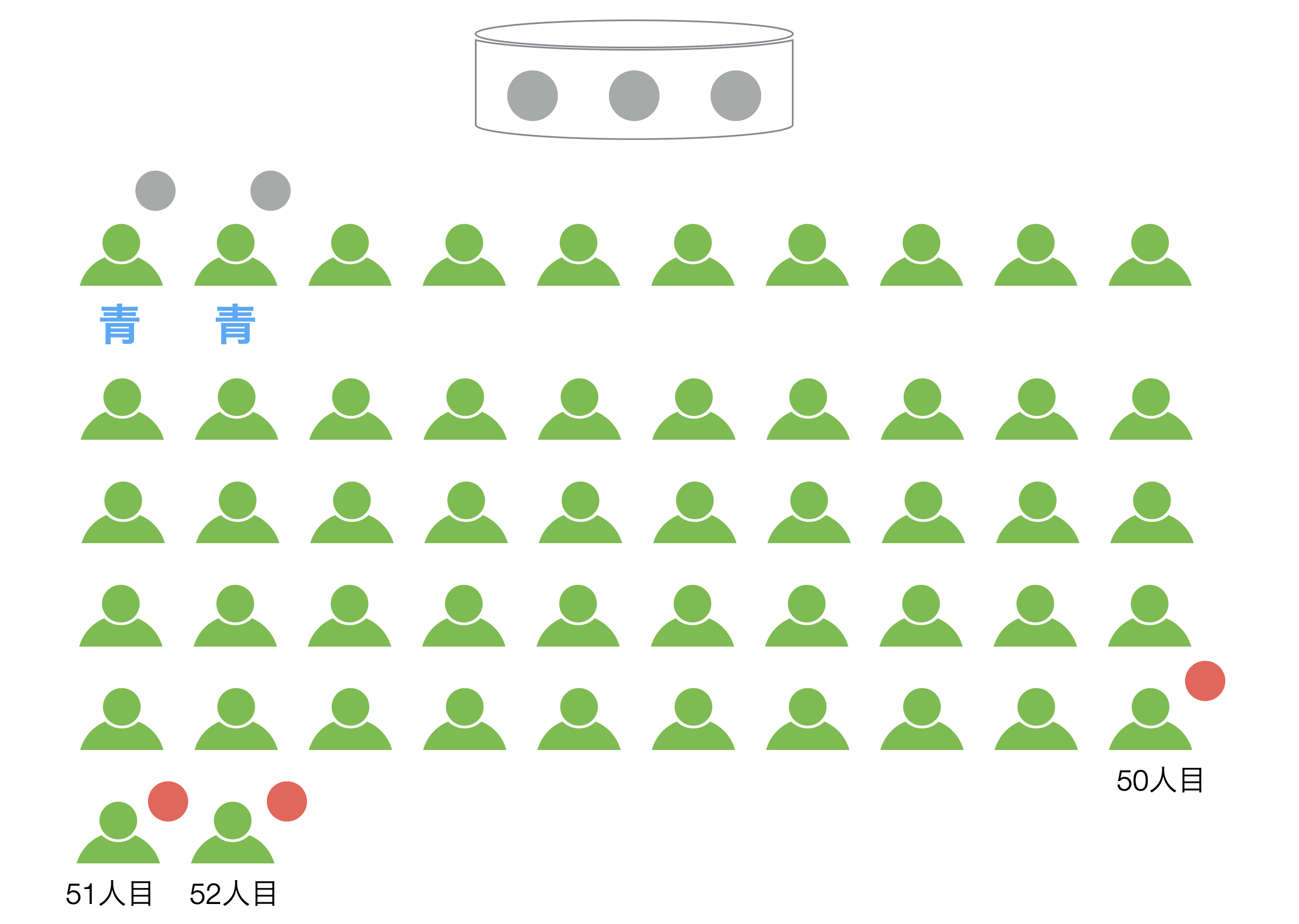
それは、ある途中で、例えば50人目の人が赤を引いたときに、自分には「赤が出た」ということをコソッと他の人に教えてしまうのです。
「コソッと」と書いたのは、上記の実験では自分の「プライベート」情報は他人には教えないと想定されているからです。
さらに、51人目の人も赤が出た場合、同じように自分には「赤が出た」ということをコソッと他の人に教えてしまうのです。
ここで、この50人目と51人目の人は例え自分に赤が出たとしても、上記で見たようにその時点で持っている「パブリック」情報によると「青が圧倒的に多数派」なわけですから、それまでの人たちと同様に「青が多数派」と発表するでしょう。
しかし、ここで次の52人目の人の意思決定に関して考えてみましょう。
まず、最初の2人より後の人達の「パブリック」情報は、自分に青が出ようが赤が出ようが「青が多数派」だと発表していることになるので当てにならない情報と言えます。しかし、最初の2人の「パブリック」情報にはその人達の「プライベート」情報が反映されていると考えることができるので、彼らの「パブリック」情報はクオリティの高い情報と言えます。
そして、直前の2人である50人目、51人目は「赤が出た」という「プライベート」情報を教えてくれたので、この情報はクオリティの高い情報と言えます。
そうすると、最初の2回青が出て(クオリティの高いパブリック情報)、直前の2回赤が出た(信頼できるプライベート情報)ということを52人目の人は知っているわけです。
そこで、この52人目の人が容器からボールを取り出し、赤が出たらどうでしょうか?
この時点で、この52人目の人にとってのクオリティの高い情報を元にすると、赤が出やすいということなり、そうすると最適な答えは「赤が多数派」となります。
ここで、これまでの「情報カスケード」が崩壊します。
もちろん、完全に崩壊するわけではありません。次の数人に青が立て続けに出た場合、やはり「青が多数派」だと決定する方向へ戻ることになるかもしれません。
しかし、もし容器の中は「赤が多数派」だとすると、実際には青が出続ける確率は低く、むしろ赤が出る確率の方が高いため、「崩壊」しやすくなります。
ここでのポイントは、一見無敵に見える「情報カスケード」も実はちょっとしたことで、例えば今回は50番目と51番目の人が他の人に「プライベート」情報を言いふらしてしまう、といったことで「崩壊」してしまう可能性を含んでいるということです。
復習:情報カスケードの3つの重要な点
もう一度この情報カスケードについての重要な3つの点をまとめます。
1. 「頭が良い」集団ほど羊になりやすい
それぞれの人達が下す意思決定は論理的には正しいものであったとしても、みんなで間違ってしまうことがある。そして、そうした状況はいとも簡単に作れてしまうのです。つまり、みんなが羊のように間違ったことでも従い続けてしまうのは、みんなの頭が悪いからではなく、むしろ頭が良い人のほうがより論理的に考えることができ、さらにより最適な答えを見つけることができるわけですから、より間違った情報でもずっと従い続けてしまうことになるのです。
2. 現実世界では「パブリック」情報を元に意思決定を行う
確率的には低いようなことでも、または起きていないことでも、最初の数人があることを「正しい」と発表してしまうと、その後何人の人がそれとは違うことを自分の目で見たり経験したりしたとしても、「パブリック」つまり一般的に広まっている認識を覆すことはできず、いつまで経っても真実(または正解)に近づいていくことができないのです。
「プライベート」な情報においては確率論が機能している、つまりより多くの人が参加すればするほど大数の法則が効いて、真の姿に近づいていくのですが、実際に私達が生きている世界では、私達は「プライベート」情報だけで意思決定をするわけで花ありません。多くの場合、「パブリック」情報をもとに、例えば「このレストランに行こう」といった意思決定を行っているのです。
正確には「パブリック」情報と「プライベート」情報の両方を使って意思決定を行うことになりますが、この違いを意識しながら意思決定を行うのは至難の業です。
3. 情報カスケードは強力だが脆くもある
この情報カスケードの罠を破るためには、一般的にこうだ、と認識されていたとしても、自分の目で確認し、それをどんなやり方であったとしても、他の人に伝えることが重要になります。
ソ連のような共産主義国家は、そうした国に住む人、またはそこに訪れ現地に住む庶民と政府の監視なしで交流したことのある人であれば、当時一般に言われていたような「楽園」でも「豊かで理想的な世界」でもないことはわかっていました。しかし、監視が行き渡り強度な言論統制が徹底されていた世界では「プライベート」な情報を「パブリック」に共有することができなかったので、いつまで経ってもみんながその「間違った」システムに従い続けることになってしまったのです。
そこに変化を与えたのは、例えば「収容所群島」などの著作を通して共産主義社会の現実を「パブリック」な世界に向けて描写したソルジェニーツィンや、徐々に増え始めた身の危険を犯してでも真実を語る人たちです。そうして、ソ連、または共産主義に支配されていた東ヨーロッパに住む多くの人達が自分の経験を元に「何かおかしい」と思うことが自分だけが持つ特有な認識というわけではなく、それが実は「多数派」なのだと認識し始めたのです。そうしてソ連や東ヨーロッパの共産主義国家は崩壊していくことになりました。(もちろん、他にも様々な要素があったと思いますが、情報、認識という点において大きな変化を共産主義国家内部の社会にもたらせたことは否定できない事実だと思います。)
あとがき
もちろん、「情報カスケード」は何も過去に起きたことや実験室での出来事だけにあてはまるわけではありません。
現在、今これを読んでいる間にも同じようなことがあなたの身の回りにも起きているのではないでしょうか。立ち止まって考えてみてください。
マスコミが「これが事実だ」と取り上げるニュースによって作り上げられた世界が自分の経験、認識している世界とかけ離れていることはないでしょうか。または自分の周りに起きていることだが、マスコミには一切出てこないので、自分の周りだけでたまたま起きていると思い込むようなことはないでしょうか。この3年の間のコロナに関連するマスコミの報道にはこの「情報カスケード」の例をたくさん見ることができます。
昔のように一日の限られた時間に触れる新聞やテレビだけでなく、今ではスマホに目を向ける時間が多くなりました。これは様々な情報に「リアルタイム」で目を通すことができるというメリットもありますが、逆にそこで目にする情報は全て「パブリック」情報で、その量は以前に比べ圧倒的に増えているのですから「情報カスケード」にハマりやすく、さらに抜け出しにくくなるというデメリットもあるのです。
そこで、「パブリック」な情報を鵜呑みにし、その洪水を毎日浴び続け、「情報量」が多いと思いこんでしまうのではなく、自分の「プライベート」情報を増やしていくようにしましょう。
例えば以下のように「プライベート」な情報を増やしていくことができます。
- 自分から外に出ていって様々な人と触れ合い、意見を交換する。
- 新しいことや趣味を始めるなど実際に自分で直接体験する時間を作る。
- ある政治家がこう言っていたというメディアの「切り取り」報道を鵜呑みにするのではなく、直接その人の発言を聞く、読む。
- メディアや政府が出してくる数字やチャートを鵜呑みにするのではなく、自分でデータを取得し、自分の目で見る、検証する。
そしてここが重要なポイントですが、自分が直接見た、聞いた、体験した、さらにデータを使ってわかったことは、隠すことなく、そして嘘をつくことなく他の人達にも積極的に伝えていきましょう。そうすることで、あたなは「問題」の一部になるのではなく、間違った「情報カスケード」を崩壊させる「解決」の一部となることができるのです。
情報は多くなるばかりです。他人の報告に頼るのではなく、より多くの人が自分の手でデータを元に現実世界を理解し、わかったことを自由に発信していけるような世界が早急に求められると思います。
以上。
データサイエンス・ブートキャンプ・トレーニング 1月&3月開催!
現在来年1月と3月のデータサイエンス・ブートキャンプへの参加を受付中です!
データサイエンス、統計の手法、データ分析を1から体系的に学ぶことで、ビジネスの現場で使える実践的なスキルを身につけたいという方は、ぜひこの機会に参加をご検討ください!
ビジネスのデータ分析だけでなく、日常生活やキャリア構築にも役立つデータリテラシー、そして「よりよい意思決定」をしていくために必要になるデータをもとにした科学的思考もいっしょに身につけていただけるトレーニングとなっております。(リンク)