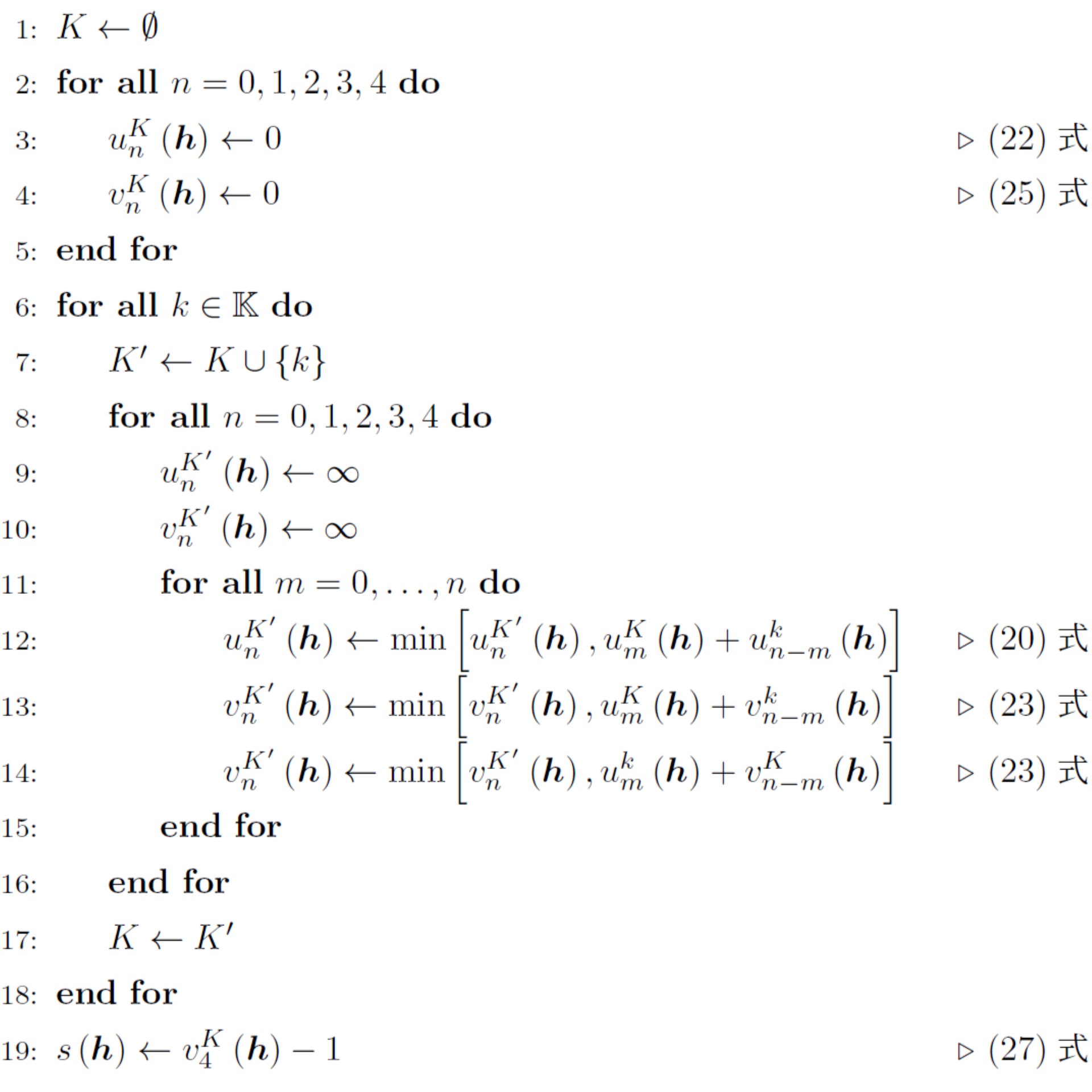はじめに
本記事では、麻雀で向聴数(シャンテン数)を計算するプログラムを作成するときに必要になる計算アルゴリズムについて解説します。以下の記事を参考にして、私なりに解釈したものを記述しています。内容が似ている部分がありますが、ご了承ください。ぜひ、以下の記事も閲覧してください。個人的な備忘録として本記事を投稿していますが、これを読んでいる皆様の理解の助けになれたら幸いです。
記号定義
| 記号 | 名称 | 説明 |
|---|---|---|
| $ \mathbb{N} $ | 自然数集合 | 0以上の整数の集合 |
| $ \mathbb{K} $ | 牌種類 | 4つの牌の種類 $ \left\{ \mathrm{m}, \mathrm{p}, \mathrm{s}, \mathrm{z} \right\} $ (それぞれ萬子, 筒子, 索子, 字牌を意味する。) |
| $ \mathbb{P} $ | 牌集合 | 34種類の牌の集合 $ \left\{ \mathrm{1\text{-}m}, \ldots, \mathrm{9\text{-}m}, \mathrm{1\text{-}p}, \ldots, \mathrm{9\text{-}p}, \mathrm{1\text{-}s}, \ldots, \mathrm{9\text{-}s}, \mathrm{1\text{-}z}, \ldots, \mathrm{7\text{-}z} \right\} $ |
| $ \mathbb{H} $ | 牌数ベクトル空間 | 取りうる牌数ベクトルの集合 $ \left( \mathbb{H} = { \left\{ 0, 1, 2, 3, 4 \right\} }^{34} \right) $ |
| $ \mathbb{W} $ | 和了形空間 | 牌数ベクトルの要素のうち、和了できる手牌であるものの集合 $ \left( \mathbb{W} \subset \mathbb{H} \right) $ |
| $ {P}^{k} $ | $ k $-部分牌集合 | 牌種類が$ k \in \mathbb{K} $である牌の集合 $ \left( P^k \subset \mathbb{P} \right) $ |
| $ {U}^{k}_{n} $ | $ k $ - $ n $面子集合 | 牌種類$ k \in \mathbb{K} $のみで構成する$ n \in \mathbb{N} $個の面子の組み合わせの集合(槓子は考慮しない)$ \left( {U}^{k}_{n} \subset \mathbb{H} \right) $ |
| $ {U}^{K}_{n} $ | $ K $ - $ n $面子集合 | 牌種類部分集合$ K \subseteq \mathbb{K} $に含まれている牌種類のみで構成する$ n \in \mathbb{N} $個の面子の組み合わせの集合(槓子は考慮しない)$ \left( {U}^{K}_{n} \subset \mathbb{H} \right) $ |
| $ {V}^{k}_{n} $ | $ k $ - $ n $面子1雀頭集合 | 牌種類$ k \in \mathbb{K} $のみで構成する$ n \in \mathbb{N} $個の面子と1個の雀頭の組み合わせの集合(槓子は考慮しない)$ \left( {V}^{k}_{n} \subset \mathbb{H} \right) $ |
| $ {V}^{K}_{n} $ | $ K $ - $ n $面子1雀頭集合 | 牌種類部分集合$ K \subseteq \mathbb{K} $に含まれている牌種類のみで構成する$ n \in \mathbb{N} $個の面子と1個の雀頭の組み合わせの集合(槓子は考慮しない)$ \left( {V}^{K}_{n} \subset \mathbb{H} \right) $ |
| $ r $ | 置換数関数 | ある牌数ベクトルを別の牌数ベクトルに置換するために必要な回数を求める関数 $ \left( r : \mathbb{H} \times \mathbb{H} \to \mathbb{N} \right) $ |
| $ s $ | 向聴数関数 | 手牌の向聴数を求める関数 $ \left( s : \mathbb{H} \to \mathbb{N} \cup \left\{ -1 \right\} \right) $ |
前提
和了形には、4面子1雀頭と七対子と十三么九の3種類がある。本記事で考慮する向聴数は、4面子1雀頭までの向聴数のみである。
距離
牌数ベクトル$ \boldsymbol{h} \in \mathbb{H} $の牌$ p \in \mathbb{P} $の牌数を$ h_p $とする。任意の$ p $に対して、$ h_p \geq h^\prime_p $にするために必要な最小の自摸回数を、距離$ d \left( \boldsymbol{h}, \boldsymbol{h}^\prime \right) $と定義する。ただし、自摸牌は自由に選択できるとする。
牌$ p $に対して、$ h_p \geq h_p^\prime $のときは、牌$ p $を自摸しなくて良い。牌$ p $に対して、$ h_p \lt h_p^\prime $のときは、$ h_p^\prime - h_p $個自摸する必要がある。したがって、距離関数$ d $は以下のように定義できる。
d \left( \boldsymbol{h}, {\boldsymbol{h}}^{\prime} \right) \stackrel{\mathrm{def}}{=} \sum_{p \in \mathbb{P}} \max \left( 0, h_{p}^{\prime} - h_{p} \right) \tag{1}
ここで定義する距離$ d $は、数学的な距離が満たす公理を一部満たしていない。距離の公理には、以下の4つがある。
- 非負性 : $ d \left( \boldsymbol{x}, \boldsymbol{y} \right) \geq 0$
- 同一律 : $ d \left( \boldsymbol{x}, \boldsymbol{y} \right) = 0 \iff \boldsymbol{x} = \boldsymbol{y} $
- 対称律 : $ d \left( \boldsymbol{x}, \boldsymbol{y} \right) = d \left( \boldsymbol{y}, \boldsymbol{x} \right) $
- 劣加法性 : $ d \left( \boldsymbol{x}, \boldsymbol{z} \right) \geq d \left( \boldsymbol{x}, \boldsymbol{y} \right) + d \left( \boldsymbol{y}, \boldsymbol{z} \right) $
しかし、定義する距離$ d $は以下のみを満たす。
- 非負性 : $ d \left( \boldsymbol{x}, \boldsymbol{y} \right) \geq 0$
- 同一律(緩和版) : $ d \left( \boldsymbol{x}, \boldsymbol{x} \right) = 0$
上記の条件を満たす場合は、「前距離(premetric)」と名称される。よって、定義した距離関数$ d $は、数学的には前距離関数であるが、ここでは単に距離関数と呼ぶことにする。
置換数
牌数ベクトル$ \boldsymbol{h} \in \mathbb{H} $の置換数$ r \left( \boldsymbol{h} \right) $を、任意の和了形$ \boldsymbol{w} \in \mathbb{W} $までの距離$ d \left( \boldsymbol{h}, \boldsymbol{w} \right) $の最小値と定義する。
r \left( \boldsymbol{h} \right) \stackrel{\mathrm{def}}{=} \min_{\boldsymbol{w} \in \mathbb{W}} d \left( \boldsymbol{h}, \boldsymbol{w} \right) \tag{2}
意味としては、任意の和了形$ \boldsymbol{w} $に対して、牌数ベクトル$ \boldsymbol{h} $の方が、$ \boldsymbol{w} $より個数が少ない牌を不足分だけ自摸する回数をそれぞれ求めて、その最小値を置換数としている。
向聴数
置換数は、和了形にするための必要な最小の自摸回数を表している。向聴数は、聴牌までに必要な自摸回数の最小値と麻雀では定義される。よって、牌数ベクトル$ \boldsymbol{h} \in \mathbb{H} $の向聴数$ s \left( \boldsymbol{h} \right) $を、置換数$ r \left( \boldsymbol{h} \right) $から1だけ引いた数と定義する。
s \left( \boldsymbol{h} \right) \stackrel{\mathrm{def}}{=} r \left( \boldsymbol{h} \right) - 1 \tag{3}
計算方針
麻雀の特性上、置換数と向聴数は牌種類ごとに分けて計算することができる。牌数ベクトル$ \boldsymbol{h} \in \mathbb{H} $において、牌種類が$ k \in \mathbb{K} $に対応する要素のみに着目する。牌数ベクトル$ \boldsymbol{h} $を、牌種類$ k $のみで構成する、0個から4個の面子の組み合わせ、または0個から4個の面子と1個の雀頭の組み合わせにするための必要な最小の自摸回数を$ {r}_{k} $とする。ただし、雀頭は1つの牌種のみに存在するとする。
このとき、置換数$ r \left( \boldsymbol{h} \right) $と向聴数 $ s \left( \boldsymbol{h} \right) $は以下のように表すことができる。
\begin{align}
r \left( \boldsymbol{h} \right) &= \sum_{k \in \mathbb{K}} {r}_{k} \tag{4} \\
s \left( \boldsymbol{h} \right) &= \sum_{k \in \mathbb{K}} {r}_{k} - 1 \tag{5}
\end{align}
置換数・向聴数の計算
計算方針で述べたように、置換数は牌種類ごとに分けて計算することを考慮する。牌種類が$ k \in \mathbb{K} $である牌の集合を、$ k $-部分牌集合$ {P}^{k} \subset \mathbb{P} $とする。このとき、牌数ベクトル$ \boldsymbol{h} \in \mathbb{H} $と牌種類$ k \in \mathbb{K} $に対して、$ \boldsymbol{h}^{k} \in \mathbb{H} $を以下を満たすように定義する。
h^{k}_{p} =
\left\{
\begin{array}{ll}
{h}_{p} & \left( p \in {P}^{k} \right) \\
0 & \left( p \notin {P}^{k} \right)
\end{array}
\right. \tag{6}
牌種類が$ k $に対応する要素は$ \boldsymbol{h} $での要素の値として、牌種類が$ k $以外に対応する要素を0としている。
このとき、置換数$ r \left( \boldsymbol{h} \right) $は以下のように表すことができる。
\begin{align}
r \left( \boldsymbol{h} \right)
&= \min_{\boldsymbol{w} \in \mathbb{W}} d \left( \boldsymbol{h}, \boldsymbol{w} \right) \\
&= \min_{\boldsymbol{w} \in \mathbb{W}} \sum_{k \in \mathbb{K}} d \left( \boldsymbol{h}^{k}, \boldsymbol{w}^{k} \right)
\end{align}
\tag{7}
牌種類が2個の場合
牌数ベクトル$ \boldsymbol{h}^{\left\{ k_1, k_2 \right\}} \in \mathbb{H} $は、2個の牌種類$ k_1, k_2 \in \mathbb{K} $のみで構成しているとする。
このとき、最も置換数が小さい和了形は必ず牌種類$ k_1, k_2 $のみで構成する。
ここで、牌種類$ k \in \mathbb{K} $のみで構成する$ n \in \mathbb{N} $個の面子の組み合わせを、$ k $ - $ n $面子集合$ U^k_n \subset \mathbb{H} $と定義する。そして、牌種類$ k $のみで構成する$ n $個の面子と1個の雀頭の組み合わせを、$ k $ - $ n $面子1雀頭集合$ V^k_n \subset \mathbb{H} $と定義する。ただし、$ U^k_n, V^k_n $において、槓子は考慮しない。例えば、$ U^\mathrm{m}_1, V^\mathrm{z}_2 $は以下のようになる。
\begin{array}{cc}
{U}^{\mathrm{m}}_{1} =
\left\{
\begin{array}{c}
\left( 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, \ldots, 0 \right) & \text{(1-mの刻子)} \\
\left( 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, \ldots, 0 \right) & \text{(2-mの刻子)} \\
\vdots & \vdots \\
\left( 0, 0, 0, 0, 0, 0, 0, 0, 3, 0, \ldots, 0 \right) & \text{(9-mの刻子)} \\
\left( 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, \ldots, 0 \right) & \text{(1-m, 2-m, 3-mの順子)} \\
\left( 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, \ldots, 0 \right) & \text{(2-m, 3-m, 4-mの順子)} \\
\vdots & \vdots \\
\left( 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, \ldots, 0 \right) & \text{(7-m, 8-m, 9-mの順子)} \\
\end{array}
\right\} \\
\\
{V}^{\mathrm{z}}_{2} =
\left\{
\begin{array}{cc}
\left( 0, \ldots, 0, 3, 3, 2, 0, 0, 0, 0 \right) & \text{(1-z, 2-zの刻子と3-zの雀頭)} \\
\left( 0, \ldots, 0, 3, 3, 0, 2, 0, 0, 0 \right) & \text{(1-z, 2-zの刻子と4-zの雀頭)} \\
\vdots & \vdots \\
\left( 0, \ldots, 0, 3, 3, 0, 0, 0, 0, 2 \right) & \text{(1-z, 2-zの刻子と7-zの雀頭)} \\
\left( 0, \ldots, 0, 2, 3, 3, 0, 0, 0, 0 \right) & \text{(2-z, 3-zの刻子と1-zの雀頭)} \\
\left( 0, \ldots, 0, 0, 3, 3, 2, 0, 0, 0 \right) & \text{(2-z, 3-zの刻子と4-zの雀頭)} \\
\vdots & \vdots \\
\left( 0, \ldots, 0, 0, 3, 3, 0, 0, 0, 2 \right) & \text{(2-z, 3-zの刻子と7-zの雀頭)} \\
\left( 0, \ldots, 0, 2, 0, 3, 3, 0, 0, 0 \right) & \text{(3-z, 4-zの刻子と1-zの雀頭)} \\
\vdots & \vdots \\
\left( 0, \ldots, 0, 0, 0, 0, 0, 2, 3, 3 \right) & \text{(6-z, 7-zの刻子と5-zの雀頭)} \\
\end{array}
\right\}
\end{array}
牌種類が$ k_1, k_2 $の2個の場合、和了形の集合$ W^{\left\{ k_1 k_2 \right\}} \subset \mathbb{W} $は以下のように表すことができる。
\begin{align}
{W}^{\left\{ k_1, k_2 \right\}}
&=
\left[ \bigcup_{n = 0}^{4} \left( {U}^{{k}_{1}}_{n} \times {V}^{{k}_{2}}_{4 - n} \right) \right] \cup
\left[ \bigcup_{n = 0}^{4} \left( {U}^{{k}_{2}}_{n} \times {V}^{{k}_{1}}_{4 - n} \right) \right] \\
&=
\left[
\bigcup_{n = 0}^{4} \left\{
\boldsymbol{u} + \boldsymbol{v} | \boldsymbol{u} \in {U}^{{k}_{1}}_{n}, \boldsymbol{v} \in {V}^{{k}_{2}}_{4 - n}
\right\}
\right] \cup
\left[
\bigcup_{n = 0}^{4} \left\{
\boldsymbol{u} + \boldsymbol{v} | \boldsymbol{u} \in {U}^{{k}_{2}}_{n}, \boldsymbol{v} \in {V}^{{k}_{1}}_{4 - n}
\right\}
\right]
\end{align}
\tag{8}
$ \left( 7 \right), \left( 8 \right) $式を用いると、牌種類が$ k_1, k_2 $の2個の場合の置換数$ r^{\left\{ k_1, k_2 \right\}} \left( \boldsymbol{h} \right) $は、以下のように表すことができる。
\begin{align}
{r}^{\left\{ {k_1}, {k}_{2} \right\}} \left( \boldsymbol{h}^{\left\{ {k_1}, {k}_{2} \right\}} \right)
&=
\min_{\boldsymbol{w} \in {W}^{\left\{ {k_1}, {k}_{2} \right\}}} \sum_{k \in \left\{ {k}_{1}, {k}_{2} \right\}} d \left( \boldsymbol{h}^{k}, \boldsymbol{w}^{k} \right) \\
&=
\min_{0 \leq n \leq 4} \left\{
\min \left[
\min_{\boldsymbol{w} \in {U}^{{k}_{1}}_{n} \times {V}^{{k}_{2}}_{4 - n}}
\sum_{k \in \left\{ {k}_{1}, {k}_{2} \right\}} d \left( \boldsymbol{h}^{k}, \boldsymbol{w}^{k} \right),
\min_{\boldsymbol{w} \in {U}^{{k}_{2}}_{n} \times {V}^{{k}_{1}}_{4 - n}}
\sum_{k \in \left\{ {k}_{1}, {k}_{2} \right\}} d \left( \boldsymbol{h}^{k}, \boldsymbol{w}^{k} \right)
\right]
\right\} \\
&=
\min_{0 \leq n \leq 4} \left\{
\min \left[
\min_{\boldsymbol{u} \in {U}^{{k}_{1}}_{n}, \boldsymbol{v} \in {V}^{{k}_{2}}_{4 - n}}
\sum_{k \in \left\{ {k}_{1}, {k}_{2} \right\}} d \left( \boldsymbol{h}^{k}, \boldsymbol{u} + \boldsymbol{v} \right),
\min_{\boldsymbol{u} \in {U}^{{k}_{2}}_{n}, \boldsymbol{v} \in {V}^{{k}_{1}}_{4 - n}}
\sum_{k \in \left\{ {k}_{1}, {k}_{2} \right\}} d \left( \boldsymbol{h}^{k}, \boldsymbol{u} + \boldsymbol{v} \right)
\right]
\right\}\\
&=
\min_{0 \leq n \leq 4} \left\{
\min \left[
\min_{\boldsymbol{u} \in {U}^{{k}_{1}}_{n}} d \left( \boldsymbol{h}^{{k}_{1}}, \boldsymbol{u} \right) +
\min_{\boldsymbol{v} \in {V}^{{k}_{2}}_{4 - n}} \left( \boldsymbol{h}^{{k}_{2}}, \boldsymbol{v} \right),
\min_{\boldsymbol{u} \in {U}^{{k}_{2}}_{n}} d \left( \boldsymbol{h}^{{k}_{2}}, \boldsymbol{u} \right) +
\min_{\boldsymbol{v} \in {V}^{{k}_{1}}_{4 - n}} \left( \boldsymbol{h}^{{k}_{1}}, \boldsymbol{v} \right)
\right]
\right\}
\end{align}
\tag{9}
ここで、部分置換数$ u^k_n \left( \boldsymbol{h}^{ \left\{ k_1, k_2 \right\} } \right), v^k_n \left( \boldsymbol{h}^{\left\{ k_1, k_2 \right\}} \right) $を以下のように定義する。
\begin{align}
u^k_n \left( \boldsymbol{h}^{\left\{ k_1, k_2 \right\}} \right) &\stackrel{\mathrm{def}}{=} \min_{\boldsymbol{u} \in U^k_n} d \left( \boldsymbol{h}^k, \boldsymbol{u} \right) \tag{10} \\
v^k_n \left( \boldsymbol{h}^{\left\{ k_1, k_2 \right\}} \right) &\stackrel{\mathrm{def}}{=} \min_{\boldsymbol{v} \in V^k_n} d \left( \boldsymbol{h}^k, \boldsymbol{v} \right) \tag{11}
\end{align}
$ \left( 9 \right), \left( 10 \right), \left( 11 \right) $式を用いると、牌種類が$ k_1, k_2 $の2個の場合の置換数$ {r}^{k_1, k_2} \left( \boldsymbol{h} \right) $は、以下のように表すことができる。
\begin{equation}
{r}^{\left\{ k_1, k_2 \right\}} \left( \boldsymbol{h}^{\left\{ k_1, k_2 \right\}} \right) =
\min_{0 \leq n \leq 4} \left\{
\min \left[
{u}^{{k}_{1}}_{n} \left( \boldsymbol{h}^{k_1} \right) + {v}^{{k}_{2}}_{4 - n} \left( \boldsymbol{h}^{{k}_{2}} \right),
{u}^{{k}_{2}}_{n} \left( \boldsymbol{h}^{k_2} \right) + {v}^{{k}_{1}}_{4 - n} \left( \boldsymbol{h}^{{k}_{1}} \right)
\right]
\right\}
\end{equation}
\tag{12}
部分置換数$ u^k_n \left( \boldsymbol{h}^k \right), v^k_n \left( \boldsymbol{h}^{k} \right) $を事前に計算して、その結果を保存することで、高速に置換数$ {r}^{k_1, k_2} \left( \boldsymbol{h}^{\left\{ k_1, k_2 \right\}} \right) $を計算することができる。
ここで、以下の関係が成り立つ。
\begin{align}
\boldsymbol{h}, \boldsymbol{h}^{\prime} \in \mathbb{H}, {k}_{1}, {k}_{2} \in \left\{ \mathrm{m}, \mathrm{p}, \mathrm{s} \right\}, n \in \mathbb{N}, \forall i, {h}_{i \text{-} {k}_{1}} = {h}^{\prime}_{i \text{-} {k}_{2}} \implies
{u}^{{k}_{1}}_{n} \left( \boldsymbol{h}^{{k}_{1}} \right) &= {u}^{{k}_{2}}_{n} \left( {\boldsymbol{h}^{\prime}}^{{k}_{2}} \right) \tag{13} \\
\boldsymbol{h}, \boldsymbol{h}^{\prime} \in \mathbb{H}, {k}_{1}, {k}_{2} \in \left\{ \mathrm{m}, \mathrm{p}, \mathrm{s} \right\}, n \in \mathbb{N}, \forall i, {h}_{i \text{-} {k}_{1}} = {h}^{\prime}_{i \text{-} {k}_{2}} \implies
{v}^{{k}_{1}}_{n} \left( \boldsymbol{h}^{{k}_{1}} \right) &= {v}^{{k}_{2}}_{n} \left( {\boldsymbol{h}^{\prime}}^{{k}_{2}} \right) \tag{14} \\
\end{align}
数牌において、すべての番号に対して、対応する牌の枚数同士が同じ場合は、部分置換数が同じであることを意味する。これより、部分置換数は数牌と字牌の2種類を求めるだけで良い。
牌種類が4個の場合
$ \left( 10 \right), \left( 11 \right) $式と同様にして、牌数ベクトル$ \boldsymbol{h} \in \mathbb{H} $と牌種類$ k \in \mathbb{K} $と面子数$ n \in \mathbb{N} $に対して、部分置換数$ u^k_n \left( \boldsymbol{h} \right), {v}^{k}_{n} \left( \boldsymbol{h} \right) $を以下のように定義する。
\begin{align}
{u}^{k}_{n} \left( \boldsymbol{h} \right) &\stackrel{\mathrm{def}}{=} \min_{\boldsymbol{u} \in {U}^{k}_{n}} d \left( \boldsymbol{h}^{k}, \boldsymbol{u} \right) \tag{15} \\
{v}^{k}_{n} \left( \boldsymbol{h} \right) &\stackrel{\mathrm{def}}{=} \min_{\boldsymbol{v} \in {V}^{k}_{n}} d \left( \boldsymbol{h}^{k}, \boldsymbol{v} \right) \tag{16}
\end{align}
牌種類部分集合$ K \subseteq \mathbb{K} $に含まれている牌種類のみで構成する$ n \in \mathbb{N} $個の面子の組み合わせの集合(槓子は考慮しない)を、$ K $ - $ n $面子集合$ U^K_n \subset \mathbb{H} $と定義する。
牌種類部分集合$ K $に含まれている牌種類のみで構成する$ n $個の面子と1個の雀頭の組み合わせの集合(槓子は考慮しない)を、$ K $ - $ n $面子1雀頭集合$ {V}^{K}_{n} \subset \mathbb{H} $と定義する。
また、牌数ベクトル$ \boldsymbol{h} $と牌種類部分集合$ K $に対して、$ \boldsymbol{h}^{K} \in \mathbb{H} $を以下を満たすように定義する。
\begin{equation}
\boldsymbol{h}^{K} = \sum_{k \in K} \boldsymbol{h}^{k}
\end{equation}
\tag{17}
牌種類部分集合$ K $に含まれている牌種類に対応する要素は$ \boldsymbol{h} $での要素の値として、それ以外の牌種類に対応する要素を0としている。
ここで、拡張部分置換数$ u^K_n \left( \boldsymbol{h} \right), {v}^{K}_{n} \left( \boldsymbol{h} \right) $を以下のように定義する。
\begin{align}
{u}^{K}_{n} \left( \boldsymbol{h} \right) &\stackrel{\mathrm{def}}{=} \min_{\boldsymbol{u} \in {U}^{K}_{n}} d \left( \boldsymbol{h}^{K}, \boldsymbol{u} \right) \tag{18} \\
{v}^{K}_{n} \left( \boldsymbol{h} \right) &\stackrel{\mathrm{def}}{=} \min_{\boldsymbol{v} \in {V}^{K}_{n}} d \left( \boldsymbol{h}^{K}, \boldsymbol{v} \right) \tag{19}
\end{align}
$ u^K_n \left( \boldsymbol{h} \right) $について考える。$ K $を$ K_1, K_2 \subseteq K \left( K_1 \cap K_2 = \emptyset, K_1 \cup K_2 = K \right) $に分ける。このとき、$K_1$に含まれる牌種類のみで$ 0 \leq m \leq n $個の面子と、$K_2$に含まれる牌種類のみで$ n - m $個の面子を作るという場合分けができる。
よって、$ u^K_n \left( \boldsymbol{h} \right) $は以下のように表すことができる。
\begin{equation}
{u}^{K}_{n} \left( \boldsymbol{h} \right) =
\min_{0 \leq m \leq n} \left[
{u}^{{K}_{1}}_{m} \left( \boldsymbol{h} \right) + {u}^{{K}_{2}}_{n - m} \left( \boldsymbol{h} \right)
\right] \tag{20}
\end{equation}
また、以下の関係が成り立つ。
\begin{align}
K &= \left\{ k \right\} &\implies
u^K_n \left( \boldsymbol{h} \right) &= {u}^{k}_{n} \left( \boldsymbol{h} \right) \tag{21} \\
K &= \emptyset &\implies
u^K_n \left( \boldsymbol{h} \right) &= 0 \tag{22}
\end{align}
$ K $の要素数が1の場合、その要素である牌種類$ k $における$ u^k_n \left( \boldsymbol{h} \right) $が$ u^K_n \left( \boldsymbol{h} \right) $と等しくなる。$ u^k_n \left( \boldsymbol{h} \right) $は事前に計算しているので既知である。$ K $の要素数が0の場合、面子を作ることができないので、$ u^K_n \left( \boldsymbol{h} \right) = 0$となる。
$ v^K_n \left( \boldsymbol{h} \right) $について考える。$ K $を$ K_1, K_2 \subseteq K \left( K_1 \cap K_2 = \emptyset, K_1 \cup K_2 = K \right) $に分ける。
このとき、雀頭の牌種類が$ K_1 $に含まれる場合と$ K_2 $に含まれる場合で分けることができる。
さらに、$ K $に含まれる牌種類のみで$ 0 \leq m \leq n $個の面子と、$ K_2 $に含まれる牌種類のみで$ n - m $個の面子を作るという場合分けができる。
よって、$ {v}^{K}_{n} \left( \boldsymbol{h} \right) $は以下のように表すことができる。
\begin{equation}
{v}^{K}_{n} \left( \boldsymbol{h} \right) =
\min_{0 \leq m \leq n} \left\{
\min \left[
{u}^{{K}_{1}}_{m} \left( \boldsymbol{h} \right) + {v}^{{K}_{2}}_{n - m} \left( \boldsymbol{h} \right),
{u}^{{K}_{2}}_{m} \left( \boldsymbol{h} \right) + {v}^{{K}_{1}}_{n - m} \left( \boldsymbol{h} \right)
\right]
\right\} \tag{23}
\end{equation}
また、以下の関係が成り立つ。
\begin{align}
K &= \left\{ k \right\} &\implies
{v}^{K}_{n} \left( \boldsymbol{h} \right) &= {v}^{k}_{n} \left( \boldsymbol{h} \right) \tag{24} \\
K &= \emptyset &\implies
{v}^{K}_{n} \left( \boldsymbol{h} \right) &= 0 \tag{25}
\end{align}
$ K $の要素数が1の場合、その要素である牌種類$ k $における$ v^k_n \left( \boldsymbol{h} \right) $が$ v^K_n \left( \boldsymbol{h} \right) $と等しくなる。$ v^k_n \left( \boldsymbol{h} \right) $は事前に計算しているので既知である。$ K $の要素数が0の場合、面子や雀頭を作ることができないので、$ v^K_n \left( \boldsymbol{h} \right) = 0$となる。
$ K $の要素数が0, 1のとき、$ u^K_n \left( \boldsymbol{h} \right), v^K_n \left( \boldsymbol{h} \right) $の値は既知なので、$ \left( 20 \right), \left( 23 \right) $式において$ K $の要素数を2, 3, 4のように1つずつ増やして計算していけば良い。
置換数$ r \left( \boldsymbol{h} \right) $は、拡張部分置換数の定義から以下のように表すことができる。
\begin{equation}
r \left( \boldsymbol{h} \right) = {v}^{\mathbb{K}}_{4} \left( \boldsymbol{h} \right) \tag{26}
\end{equation}
また、向聴数$ s \left( \boldsymbol{h} \right) $は、$ \left( 3 \right), \left( 26 \right) $式を用いると以下のように表すことができる。
\begin{equation}
s \left( \boldsymbol{h} \right) = {v}^{\mathbb{K}}_{4} \left( \boldsymbol{h} \right) - 1 \tag{27}
\end{equation}
アルゴリズム
向聴数を計算するためのアルゴリズムの擬似コードを以下に示す。
参考文献