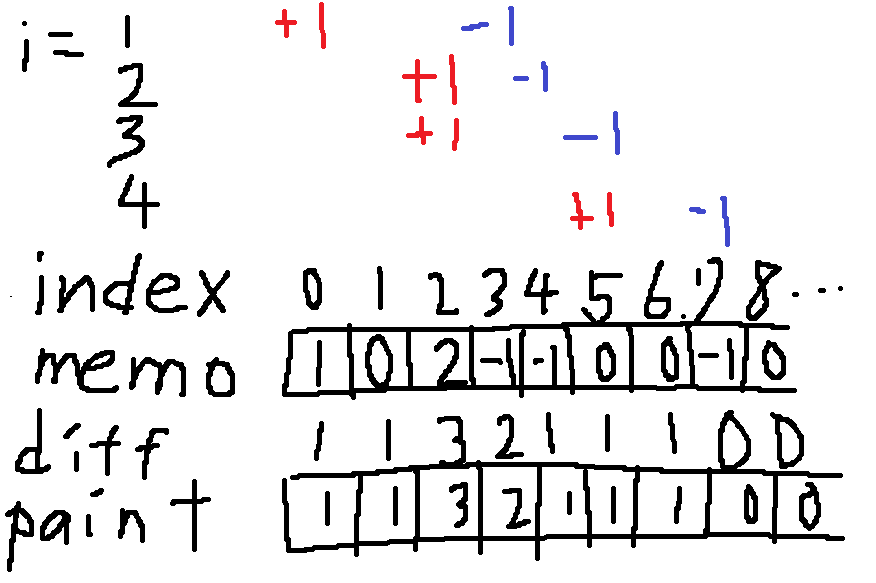読むとimos法が使えるようになる記事(1次元のみ)

はじめに

 こちらはimos法を初めて知るような初心者向けの記事となります。使いこなすまではいきませんが、簡単な1次元の問題を解けるぐらいまでは理解できるように作成しました。
imos法について図解と例題を交えて解説します。1次元のみの解説です。imos法に関しては既に分かりやすい記事が多数あったため(参考リンクへ)、正直私のアウトプット用になりますが、図解された方が分かりやすい、別の問題の例を見たいという方は是非ご一読ください。

目次

1. 用語解説
2. imos法とは
3. imos法の使用例(1次元)
4. まとめ
5. 参考リンク

1 用語解説

 簡単に用語の説明を載せておきます。これってなんだっけ？ってなった場合には戻ってきてください

• imos法(いもす法): 累積和を求める際に計算量を減らすことが出来る
• Atcoder: 競技プログラミングのサイトでいろんなアルゴリズムの問題が解ける
• AC: あるテストケースを実行した際の判定結果で正解を表す
• TLE: あるテストケースを実行した際の判定結果で実行時間超過を表す

2 imos法とは

 imos法とは、累積和などを求める際に、差分のみを記録して後から計算することによって、従来の手法より計算量を減らすことが出来る考え方です。高次元にも応用できるのが最大の特徴ですが、今回はAtcoderに出題される可能性のある1次元の話になります。imos法は

1 差分のみをメモしておく
2 メモを頼りに累積和を求める。

という2ステップで実装することが出来ます。

3 imos法の例題

imos法の例題として以下の問題を用います。こちらはAtCoderのかなり昔のC問題になります。問題見るのが手間でしたら要約を見てください。

問題

AtColor社は、0 から 1,000,000 まで 1,000,001 通りの濃さがある灰色の絵の具を販売することにしました。0 が最も黒く、1,000,000 が最も白い絵の具です。
　しかし、途方も無い数の濃さのバリエーションがある一方、消費者には細かい違いが分からないということが判明しました。これを知ったAtColor社は、売れない濃さの絵の具を生産するのはやめて、最も人気のある濃さの色の絵の具1つだけを販売することにしました。
　AtColor社は上記を達成するために、最も人気な絵の具がどのくらい売れるかをアンケート調査で調べることにしました。AtColor社がどの範囲の濃さの絵の具なら購入したいかというアンケートを消費者に対して行ったところ、「$a≦x≦b$を満たす濃さ$x$の絵の具ならば購入する」という形式の情報が$n$件得られました。
　あなたの仕事は、これらの情報から、最も多くの消費者に購入される濃さの絵の具について、その絵の具を購入する消費者の数を出力するプログラムを作ることです。

入力

$n$
$a_1$ $b_1$
$a_2$ $b_2$
…
$a_n$ $b_n$

制約

$1 ≦ n ≦ 100,000$
$0 ≦ a_i ≦ b_i ≦ 1,000,000$

問題の要約

• 最初の$n$がデータの個数
• $a_i$から$b_i$までを+1すること
• 全部処理し終わったら1番大きい数字を出力

3.1 imos法ではない解法(TLE)

 まず、最初にimos法ではない解法になります。これ以降このやり方を従来手法と呼びます。愚直にfor文で$a_i$から$b_i$までを加算することを$n$回行います。一応これで正しい答えは求まります。

Atcolor_TLE

import java.util.Scanner;

public class Atcolor_TLE {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int surveyNum = sc.nextInt();
        int[] paint = new int[1000001];
        int[] aNumbers = new int[surveyNum];
        int[] bNumbers = new int[surveyNum];

        //全てのaとbを取得
        for(int i = 0; i < surveyNum; i++) { 
            aNumbers[i] = sc.nextInt();
            bNumbers[i] = sc.nextInt();
        } 

        sc.close();
        
        //配列のaからbまで全部繰り返し足す
        for(int i = 0; i < surveyNum; i++) {
            for(int j = aNumbers[i]; j <= bNumbers[i]; j++) {
                paint[j]++;
            }
        }

        //結果の出力
        System.out.println(maxnumber(paint));
    }

    //int配列の中で一番大きい数字を返す関数
    public static int maxnumber(int[] numbers) {
        int max = 0;

        for(int i = 0; i < numbers.length; i++) {
            if (max < numbers[i]) {
                max = numbers[i];
            }
        }

        return max;
    }
}

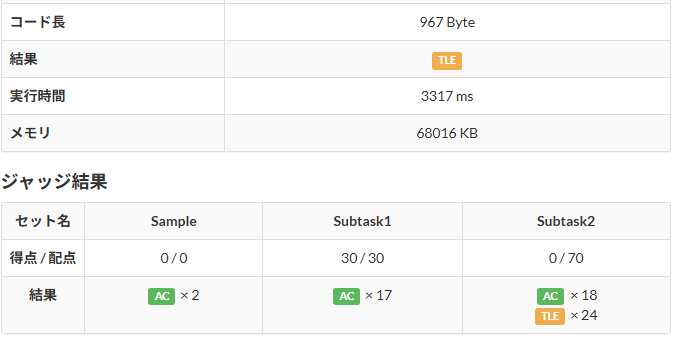
 従来手法では累積和を求める処理の部分で二重for文になってしまいます。このコードで提出した場合以下のような結果になります。

 テストケースのうち24個でTLE(実行時間超過)という結果になりました。このやり方で処理をした際に最悪のパターンを考えます。$n$は最大100,000回になり、$a_i$が0で、$b_i$が1,000,000だった時、for文を回す回数は 100,000 × 1,000,001回 になります実行時間超過してしまうのも納得です。

3.2 imos法を用いた解法

おまちかねのimos法を用いた解放になります。先にコードを見せてしまった方が早いと思います。

import java.util.Scanner;

public class Atcolor {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int surveyNum = sc.nextInt();
        int[] paint = new int[1000001];

        int a;
        int b;
        //メモのためのリストを用意しておく　※配列の大きさ+1になることに注意
        int[] memoList = new int[1000002];

        //手順1 差分のみをメモしておく
        for(int i = 0; i < surveyNum; i++) {
            a = sc.nextInt();
            b = sc.nextInt()+1;

            //開始位置では+1、終了位置では-1する
            memoList[a]++;
            memoList[b]--;
        } 

        sc.close();
        int diff = 0;

        //手順2　メモを頼りに累積和を求める
        for(int i = 0; i < paint.length; i++) {
            diff += memoList[i];
            paint[i] += diff;
        }

        //結果の出力
        System.out.println(maxnumber(paint));

    }

    //int配列の中で一番大きい数字を返す関数
    public static int maxnumber(int[] numbers) {
        int max = 0;

        for(int i = 0; i < numbers.length; i++) {
            if (max < numbers[i]) {
                max = numbers[i];
            }
        }

        return max;
    }
}

 ここでimos法の実装手順を思い出して頂きたいです。imos法は

1 差分のみをメモしておく
2 メモを頼りに累積和を求める

で実装することができました。コードにもコメントを記しておきましたが、最初のfor文で手順1の差分をメモを行います。そして、その後のfor文で手順2のメモを頼りに累積和を求めることを行います。この時メモする配列は、結果の配列のサイズ+1となることに注意してください。なぜこうなるのかというと、imos法でマイナスをする部分は+1した場所にしなければ、累積和を求める際に最後の値が誤った値になってしまうからです。例えば、$a_i$が0で$b_i$が1,000,000の時には結果の配列すべてに1が入るはずですが、マイナスをするindexに+1をしないと最後の値は0になってしまいます。

imos法の処理についてもう少し詳しく図解

 imos法のメモの部分と累積和を求める部分を入力例を用いて説明します。入力は以下になります。

入力

$n = 4$
$a_1 = 0, b_1 = 2$
$a_1 = 2, b_1 = 3$
$a_1 = 2, b_1 = 4$
$a_1 = 5, b_1 = 6$

まずメモを行いますのでint配列のmemoにそれぞれの差分をメモします。例えば$i = 1$のとき開始地点の$a_i$は0なのでindexの0のところに+1します。終了地点の$b_i$は2ですが、このまま2に代入すると、累積和を求める(結果の配列paintにdiffを足す)際にindex0,1にしか+1がされなくなってしまいます。今回では0,1,2の部分に+1したいので、終了地点は+1した場所にします。なので今回はindexが3のところに-1をします。このようにi=4まで、memo配列に書き込みます。
 その後memoの配列を頼りに、差分を表す変数diffにmemoの値を加算します。そのdiffを結果の配列paintに加算します。こうすることでfor文一回で、求めたかった配列である[1,1,3,2,1,1,1,0,…,0]を求めることができます。

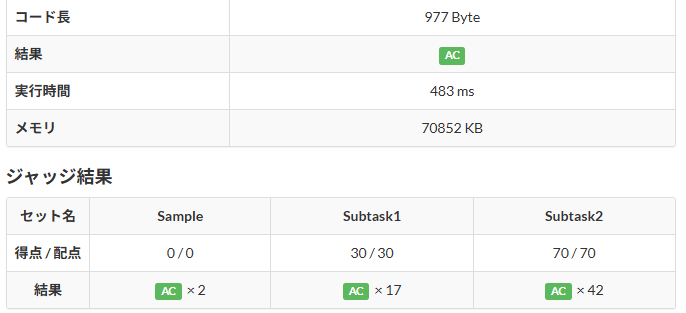
 従来の手法で最悪のパターンをこちらでも考えます。$n$は最大100,000回になり、$a_i$が0で、$b_i$が1,000,000だった時、for文を回すのはメモでデータの個数分である100,000回、累積和を求める際に配列のサイズである1,000,001回分行います。つまりimos法での最終的なfor文を回す回数は 100,000 + 1,000,001 になります。従来手法ではデータの個数と配列のサイズの積でしたが、imos法ではデータの個数と配列のサイズの和になります。これで、imos法がどれだけ、計算量を減らせているかが伝わったと思います。こちらでコードを提出すると全てACとなります。実行時間も483msとなり、従来手法が 3317msだったのを考えると、確かに短縮できています。

4 まとめ

 今回はimos法を初心者向けに紹介しました。最低限の1次元のimos法はこれで使えるようになると思います。まとめとして、覚えて欲しいことは以下のことになります。

• imos法は累積和を効率的に求めるアルゴリズムである
• imos法の実装手順
  1 差分のみをメモしておく
  2 メモを頼りに累積和を求める
• 計算量を積から和に減らすことが出来る

今後さらに知識を深めたらimos法の応用や2次元のimos法の解説も行っていきたいと思います。ここまでご一読いただき、ありがとうございました。

5 参考リンク

-いもす法の開発者様の解説 私では説明できない特殊な座標系への拡張や、多次数への拡張を解説してくれています。

-きりみんちゃん様の解説 私はこれで理解しました。とにかく分かりやすいです。