3種類の基底関数によるベイズ線形回帰の実装

はじめに

この記事は古川研究室 Workout_calendar 20日目の記事です。
本記事はベイズ線形回帰の実装をメインに行っています。理論式の方は途中計算を省いていますので、うまく計算したら次の式になるんだな程度にお考え下さい。詳しい式の導出は　最尤推定、MAP推定を用いたパラメトリック回帰(12日目の記事)にて説明します！

実装に必要なベイズ線形回帰の式

まずは、ベイズ線形回帰の予測分布の求め方を説明します。
ベイズ線形回帰は新しい観測値(測定値) $x_{new}$ を入力としたときに出力である推定値 $y_{new}$ の確率を関数のパラメータをデータセットから推定することで求めるものです。

まず、正規分布 $N(x|\mu,σ^2)$ の式は以下になります。
$σ^2=$ 分散$,$ $μ=$ 平均

N(x|\mu,σ^2)=\frac{\displaystyle1}{\displaystyle\sqrt{2π\sigma^2}}\exp\left\{-\frac{\displaystyle(x-μ)^2}{\displaystyle 2σ^2}\right\}

以上を踏まえた上で

X=\left\{(x_{1},y_{1}),(x_{2},y_{2})....(x_{n},y_{n})\right\}

$X$＝データセット
$w=$ パラメータ(ベクトルです)
$φ(x)=$ 基底関数(実装では$w,φ(x)$は10次元ベクトルとしてます)

このときの予測分布

$p(y_{new}|x_{new},X) =\underline{N(y_{new}|m^Tφ(x_{new}) ,β+φ(x_{new})^TSφ(x_{new}))}$
を求めていきます。$\beta$ と $φ(x)$はこちらで設定するので、事後分布の平均$m$と分散$S$を求めれば予測分布を求めることができます。
まず事後分布$p(w|X)$を求めます。事後分布$p(w|X)$はベイズの定理より

$p(w|X)=\frac{\displaystyle p(y|x,w)p(w)}{\displaystyle p(y|x)}$

となります。右辺の $p(y|x,w)$ は尤度で $p(w)$は事前分布です。また、どちらともガウス関数に従うと仮定します。予めこちらでパラメータ値を設定する必要があり、設定するパラメータは平均と分散です。計算の簡略化のため平均$μ=0$としてます。

$p(w)=N(w|μ,α^{-1}I)$
パラメーターはガウス関数(平均$μ=0$,分散$=α^{-1}I$)

ここでは$f(x)=w^Tφ(x)$
$p(X|w)=N(y_{n}|f(x_{n}),β^{-1})=\sqrt\frac{β}{2π}\exp\left[-\frac{β}{2}(w^Tφ(x_{n})-y_{n})^2\right]$

よって事後確率は次のようになります。

$p(w|X)\propto p(X|w)p(w)$
$=\left(p(y_{1}|x_{1},w)×…×p(y_{n}|x_{n},w)\right)×p(w)=\left({\displaystyle\prod_{n=1}^{N}p(y_{n}|x_{n},w)}\right)×p(w)$
$\ln p(w|X)=\displaystyle-\frac{1}{2}w^T(\beta\Phi^T\Phi+\alpha I)w+(\beta y^T\Phi)w+const$

ここで、事後確率は平均 $m$ 分散 $S$ の正規分布となるので

$p(w|X)=N(w|m,S)$
となります。対数をとると
$\ln p(w|X)=-\displaystyle\frac{1}{2}(w-m)^TS^{-1}(w-m)+const$

この式を先ほど求めた$\ln p(w|X)$ と係数を比較することで事後確率の平均と分散が求まります。

$S=(\beta \Phi^T\Phi+\alpha I)^{-1}$
$m=(\Phi^T\Phi+\lambda I)^{-1}\Phi^Ty$
$\lambda=\frac{\alpha}{\beta}$

以上により予測分布$\underline{N(y_{new}|m^Tφ(x_{new}) ,β+φ(x_{new})^TSφ(x_{new}))}$が求まります。

$p(y_{new}|x_{new},X) = \displaystyle\int p(y_{new}|x_{new},w)p(w|X)dw=\underline{N(y_{new}|m^Tφ(x_{new}) ,β+φ(x_{new})^TSφ(x_{new}))}$

Pythonで実装していきましょう！

ベイズ線形回帰をPythonで実装しました。実装には参考文献を大いに参考させて頂きました。
実装の流れは以下です。

予測する真の関数を定義
　　　　　↓
真の関数にノイズをのせて15個プロット
　　　　　↓
基底関数を定義（3種類）
　　　　　↓
　　計画行列の作製
　　　　　↓
事前分布のパラメーター設定
　　　　　↓
　　事後確率を計算
　　　　　↓
　　　　グラフ化

$p(y_{new}|x_{new})=\underline{N(y_{new}|m^Tφ(x_{new}) ,β+φ(x_{new})^TSφ(x_{new}))}$

目標は下線の正規分布を作って$(x_{new},y_{new})$として$x$軸の$0～1$の値と$y$軸の$－1.5～1.5$を代入することです。正規分布の分散と平均に含まれている変数は以下です。$\alpha$ と $\beta$ はハイパーパラメータなので事前にこちらで設定しておく必要があります。

$\Large平均:\large m^Tφ(x_{new})$

$φ(x):$基底関数
$m:$事後確率の平均
$m=(\Phi^T\Phi+\displaystyle\frac{α}{β}I)^{-1}\Phi y$
$α:$パラメータ $w$ の事前確率の分散の逆数
$\Phi=(φ(x_{1}),...φ(x_{n}))$

$\Large分散:\large β+φ(x_{new})^TSφ(x_{new})$

$β:$尤度の分散の逆数
$φ(x):$基底関数
$S:$事後確率の分散
$S=(β\Phi^T\Phi+αI)^{-1}$

これらの値を求めることで、グラフ化していきます。
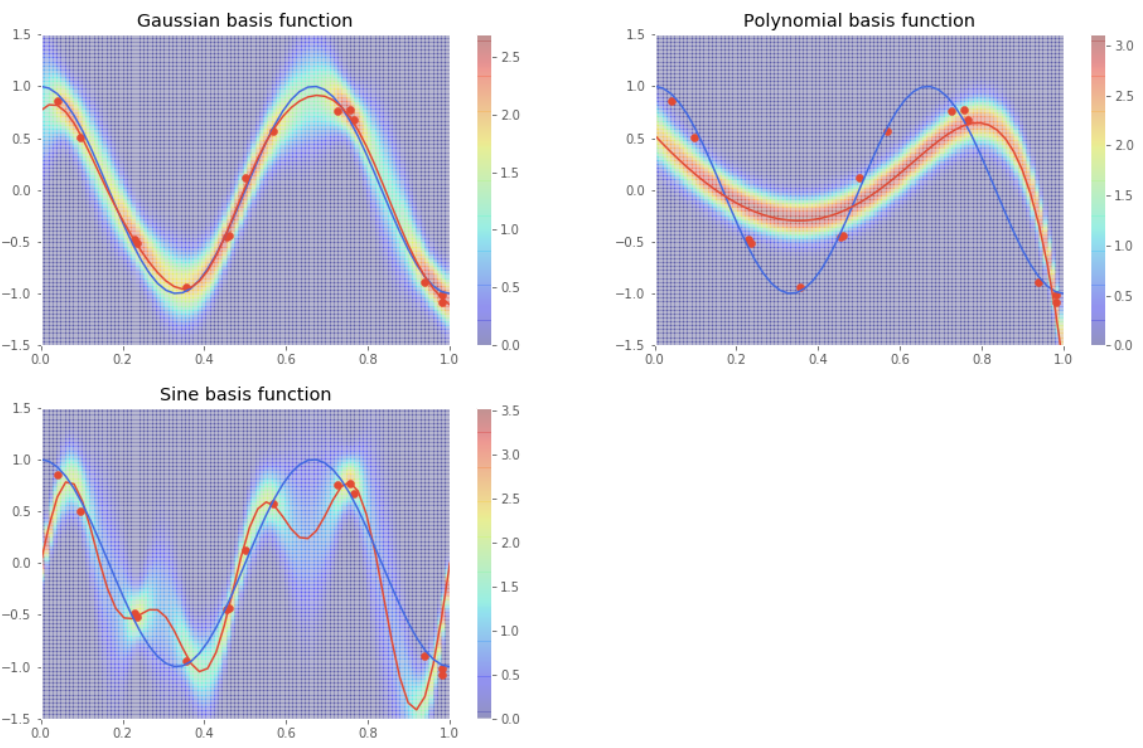
今回はガウス関数，sin関数，多項式を基底関数としてそれぞれグラフ化しました。実行結果を以下に示します。ガウス関数を基底関数に選んだ時が一番うまくフィッティング出来ています。またベイズ線形回帰では予測した結果の平均、分散がわかるので予測結果にどのくらい自信があるのかが分かります。線形回帰では得られないメリットです。

ここからpythonでのプログラムを示していきます。
まずは恒例のおまじないです。

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
plt.style.use("ggplot")

つぎにデータ点を作成します。
真の関数は $\cos(3\pi x)$ で、15個のデータ点にはノイズを加えています。

n = 15
X = np.random.uniform(0, 1, n)
T = np.cos(3 * np.pi * X) + np.random.normal(0, 0.1, n)

基底関数は3つ用意しました。(※$\theta$はパラメーターです。)
重みと基底はそれぞれ10個あります。

ガウス関数

y=\theta_{0}\exp\left\{-\frac{\displaystyle(x-μ_{0})^2}{\displaystyle 2σ^2}\right\}+\theta_{1}\exp\left\{-\frac{\displaystyle(x-μ_{1})^2}{\displaystyle 2σ^2}\right\}+...+\theta_{n}\exp\left\{-\frac{\displaystyle(x-μ_{2})^2}{\displaystyle 2σ^2}\right\}

sin関数
$y=\theta_{0}\sin(x\pi)+\theta_{1}\sin(2x\pi)+...+\theta_{n}\sin(nx\pi)$

多項式
$y=\theta_{0}+\theta_{1}x+\theta_{2}x^2+...+\theta_{n}x^n$

def phi(x):#基底関数:ガウス関数
    h = 0.1
    return np.exp(-(x - np.arange(0, 1, 0.1))**2/(2*h **2))
    
def phi2(x):#基底関数:sin関数
    m = 10
    return np.sin(x*np.pi*np.arange(0,m))
    
def phi3(x):#基底関数：多項式
    m = 10
    return x**np.arange(0,m)

計画行列を作ります。($\Phi$ のことです)
基底関数が3つあるので計画行列も3つ作ります。

Phi = np.array([phi(x) for x in X])    #ガウス関数の計画行列
Phi2 = np.array([phi2(x) for x in X])  #sin関数の計画行列
Phi3 = np.array([phi3(x) for x in X])  #多項式の計画行列

次にハイパーパラメータを設定します。
これはグラフ化した結果を見ながら、うまくいくように値を設定すればいいです。

M = 10         #基底の数
alpha = 0.01
beta = 9.0

事後分布の平均と分散です。

$m=(\Phi^T\Phi+\displaystyle\frac{α}{β}I)^{-1}\Phi y$
$S=(β\Phi^T\Phi+αI)^{-1}$

#平均
m = beta * S.dot(Phi.T).dot(T)     #ガウス関数の平均
m2 = beta * S2.dot(Phi2.T).dot(T)  #sin関数の平均
m3 = beta * S3.dot(Phi3.T).dot(T)  #多項式の平均

#分散
S = np.linalg.inv(alpha * np.eye(M) + beta * Phi.T.dot(Phi))    #ガウス関数の分散
S2 = np.linalg.inv(alpha * np.eye(M) + beta * Phi2.T.dot(Phi2)) #Sin関数の分散
S3 = np.linalg.inv(alpha * np.eye(M) + beta * Phi3.T.dot(Phi3)) #多項式の分散

では、予測分布を求めましょう。

$p(y_{new}|x_{new})=N(y_{new}|m^Tφ(x_{new}) ,β+φ(x_{new})^TSφ(x_{new}))$

def sigma(x):
    return 1.0/ beta + phi(x).dot(S).dot(phi(x))
def norm(x,y): #ガウス基底関数での予測関数
    return stats.norm(m.dot(phi(x)), sigma(x)).pdf(y)


def sigma2(x):
    return 1.0/ beta + phi2(x).dot(S2).dot(phi2(x))
def norm2(x,y): #sin基底関数での予測関数
    return stats.norm(m2.dot(phi2(x)), sigma2(x)).pdf(y)


def sigma3(x):
    return 1.0/ beta + phi3(x).dot(S3).dot(phi3(x))
def norm3(x,y): #多項式基底での予測関数
    return stats.norm(m3.dot(phi3(x)), sigma3(x)).pdf(y)

最後にグラフ化です。
グラフ化にはまずメッシュを作ります。

x_, y_ = np.meshgrid(np.linspace(0 ,1 ,100), np.linspace(-1.5, 1.5,80))

次にそれぞれの関数を出力していきます。

Z = np.vectorize(norm)(x_,y_)
Z2 = np.vectorize(norm2)(x_,y_)
Z3= np.vectorize(norm3)(x_,y_)
y = [m.dot(phi(x__)) for x__ in x]
y2 = [m2.dot(phi2(x__)) for x__ in x]
y3 = [m3.dot(phi3(x__)) for x__ in x]

plt.figure(figsize=(16, 10))

#ガウス基底関数
plt.subplot(2,2,1)
plt.xlim(0, 1)
plt.ylim(-1.5, 1.5)
plt.pcolor(x_, y_, Z,cmap='jet',alpha=0.2)
plt.colorbar()
plt.scatter(X, T)
plt.plot(np.linspace(0,1), np.cos(3 * np.pi * np.linspace(0,1)), c ="royalblue")
plt.plot(x, y)
plt.title("Gaussian basis function")

#多項式基底関数
plt.subplot(2,2,2)
plt.pcolor(x_, y_, Z3,cmap='jet',alpha=0.2)
plt.colorbar()
plt.xlim(0, 1)
plt.ylim(-1.5, 1.5)
#点のプロット
plt.scatter(X, T)
plt.plot(np.linspace(0,1), np.cos(3 * np.pi * np.linspace(0,1)), c ="royalblue")
#予測関数のプロット
plt.plot(x, y3)
plt.title("Polynomial basis function")


#sin基底関数
plt.subplot(2,2,3)
plt.pcolor(x_, y_, Z2,cmap='jet',alpha=0.2)
plt.colorbar()
plt.xlim(0, 1)
plt.ylim(-1.5, 1.5)
#点のプロット
plt.scatter(X, T)
#予測関数をプロット
plt.plot(x, y2)
plt.title("Sine basis function")


#真の関数プロット
plt.plot(np.linspace(0,1), np.cos(3 * np.pi * np.linspace(0,1)), c ="royalblue")
plt.show()
 
 
for m_ in m_list:
    x = np.linspace(0,1)
    y = [m_.dot(phi(x__)) for x__ in x]
    plt.plot(x, y, c = "r")
    plt.plot(np.linspace(0,1), np.cos(3 * np.pi * np.linspace(0,1)), c ="g")
    

plt.show()

最後に余談ですが、
3次元にプロットするとこうなります。$\cos$関数の山脈ができます。$x,y$軸は$\cos$関数の値を示しています。z軸は分散の逆数です。

3D表示にするには以下のプログラムを加えて下さい。

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter



fig = plt.figure()
ax = fig.gca(projection='3d')

surf = ax.plot_surface(y_, x_, Z2, cmap=cm.coolwarm,
                       linewidth=0, antialiased=False)

# Customize the z axis.
ax.set_zlim(0, 10)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))

# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)

plt.show()

おわりに

本記事では実装をメインに説明してきました。なかなか理論式だけを追っかけてみても、いまいち理解できないところや、ここの値は何を意味しているのかなどの疑問を解消するのは難しいです。私がそうでした。コードをいじってみることで理解を深めていければと思います！

参考文献
https://openbook4.me/sections/1563