はじめに
この記事は古川研究室 Workout_calendar 25日目の記事です。
特異値分解について理解を深める為に記事を書きました。文書の例を通してSVDで何ができるのか、何をやっているのかを示していきます!
特異値分解とは
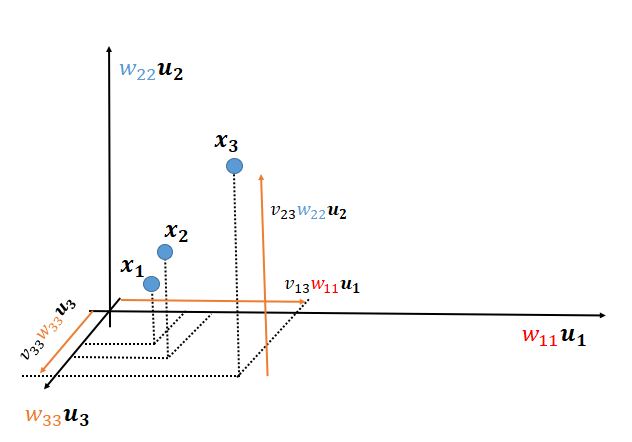
特異値分解とは任意の $m×n$ 行列 $A$ に対して $A=UΣV^T$ と表現できることです。つまり $A$ を $U,Σ,V^T$ の3つに分解できることを示しています。$U$と$V^T$は直交行列で$Σ$は対角行列です。イメージとしては下図のようになります。

しかし、これだけでは、え?何がすごいの?どこで使うの?そもそも何?といった疑問がでてくるので、本記事では文書解析を例にして、わかりやすく特異値分解を説明していきます。
特異値分解の例
ここではまず例として3×3の行列の特異値分解を使って特異値の役割及び特異値を削減することで何ができるのかを説明します。
2×3行列$A$の既に分解されている形を考えます。(色の付いている文字が特異値です$\color{red}{w_{11}}>\color{blue}{w_{22}}> \color{orange}{w_{33}}$とします)
A =
\left(
\begin{array}{c}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}\\
\end{array}
\right)
,U =
\left(
\begin{array}{c}
u_{11} & u_{12} & u_{13}\\
u_{21} & u_{22} & u_{23} \\
u_{31} & u_{32} & u_{33} \\
\end{array}
\right)
,Σ =
\left(
\begin{array}{c}
\color{red}{w_{11}} & 0& 0 \\
0 & \color{blue}{w_{22}}& 0 \\
0 & 0 & \color{orange}{w_{33}} \\
\end{array}
\right)
,V^T=
\left(
\begin{array}{c}
v_{11} & v_{12} & v_{13}\\
v_{21} & v_{22} & v_{23} \\
v_{31} & v_{32} & v_{33} \\
\end{array}
\right)
とおくと特異値分解は$A=UΣV^T$なので
A = UΣV^T=
\left(
\begin{array}{c}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}\\
\end{array}
\right)=
\left(
\begin{array}{c}
u_{11} & u_{12} & u_{13}\\
u_{21} & u_{22} & u_{23} \\
u_{31} & u_{32} & u_{33} \\
\end{array}
\right)
×
\left(
\begin{array}{c}
\color{red}{w_{11}} & 0& 0 \\
0 & \color{blue}{w_{22}}& 0 \\
0 & 0 & \color{orange}{w_{33}} \\
\end{array}
\right)
×
\left(
\begin{array}{c}
v_{11} & v_{12} & v_{13}\\
v_{21} & v_{22} & v_{23} \\
v_{31} & v_{32} & v_{33} \\
\end{array}
\right)
右辺を計算すると下式のようになるのですが、注目して欲しいのは特異値である$w_{11}$、$w_{22}$、$w_{33}$です。行列$A$の全ての要素に3つの特異値が含まれているのが分かります。よって特異値は行列$A$の各要素に与えている影響力と言えます。例えば$\color{blue}{w_{22}}=0$であれば$\color{blue}{w_{22}}$を含んでいる項が消滅して行列$A$の値に関与しないことが分かります。
A=UΣV^T=
\left(
\begin{array}{c}
\color{red}w_\color{red}{11}u_{11}v_{11}+\color{blue}w_\color{blue}{22}u_{12}v_{21}+\color{orange}w_\color{orange}{33}u_{13}v_{31} & \color{red}w_\color{red}{11}u_{11}v_{12}+\color{blue}w_\color{blue}{22}u_{12}v_{22}+\color{orange}w_\color{orange}{33}u_{13}v_{32}&\color{red}w_\color{red}{11}u_{11}v_{13}+\color{blue}w_\color{blue}{22}u_{12}v_{23}+\color{orange}w_\color{orange}{33}u_{13}v_{33}\\
\color{red}w_\color{red}{11}u_{21}v_{11}+\color{blue}w_\color{blue}{22}u_{22}v_{21}+\color{orange}w_\color{orange}{33}u_{23}v_{31} & \color{red}w_\color{red}{11}u_{21}v_{12}+\color{blue}w_\color{blue}{22}u_{22}v_{22}+\color{orange}w_\color{orange}{33}u_{22}v_{32}&\color{red}w_\color{red}{11}u_{21}v_{13}+\color{blue}w_\color{blue}{22}u_{22}v_{23}+\color{orange}w_\color{orange}{33}u_{23}v_{33}\\
\color{red}w_\color{red}{11}u_{31}v_{11}+\color{blue}w_\color{blue}{22}u_{32}v_{21}+\color{orange}w_\color{orange}{33}u_{33}v_{31} & \color{red}w_\color{red}{11}u_{31}v_{12}+\color{blue}w_\color{blue}{22}u_{32}v_{22}+\color{orange}w_\color{orange}{33}u_{32}v_{32}&\color{red}w_\color{red}{11}u_{31}v_{13}+\color{blue}w_\color{blue}{22}u_{32}v_{23}+\color{orange}w_\color{orange}{33}u_{33}v_{33}\\
\end{array}
\right)
ここで行列$A$を以下のようにします。
\boldsymbol x_{1}=
\left(
\begin{array}{c}
a_{11} \\
a_{21} \\
a_{31} \\
\end{array}
\right),
\boldsymbol x_{2}=
\left(
\begin{array}{c}
a_{12} \\
a_{22} \\
a_{32} \\
\end{array}
\right),
\boldsymbol x_{3}=
\left(
\begin{array}{c}
a_{13} \\
a_{23} \\
a_{33} \\
\end{array}
\right)
A=
\left(
\begin{array}{c}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}\\
\end{array}
\right)=
\left(
\begin{array}{c}
\boldsymbol x_{1}&\boldsymbol x_{2}&\boldsymbol x_{3}
\end{array}
\right)
次に$UΣV^T$を変形します。
\boldsymbol u_{1}=
\left(
\begin{array}{c}
u_{11} \\
u_{21} \\
u_{31} \\
\end{array}
\right),
\boldsymbol u_{2}=
\left(
\begin{array}{c}
u_{12} \\
u_{22} \\
u_{32} \\
\end{array}
\right),
\boldsymbol u_{3}=
\left(
\begin{array}{c}
u_{13} \\
u_{23} \\
u_{33} \\
\end{array}
\right)
とおくと
UΣV^T=
\left(
\begin{array}{c}
v_{11}\color{red}{w_{11}}\boldsymbol u_{1}+v_{21}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{31}\color{orange}{w_{33}}\boldsymbol u_{3}&v_{12}\color{red}{w_{11}}\boldsymbol u_{1}+v_{22}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{32}\color{orange}{w_{33}}\boldsymbol u_{3}&v_{13}\color{red}{w_{11}}\boldsymbol u_{1}+v_{23}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{33}\color{orange}{w_{33}}\boldsymbol u_{3}
\end{array}
\right)
$A=UΣV^T$より
\left(
\begin{array}{c}
\boldsymbol x_{1}&\boldsymbol x_{2}&\boldsymbol x_{3}
\end{array}
\right)=
\left(
\begin{array}{c}
v_{11}\color{red}{w_{11}}\boldsymbol u_{1}+v_{21}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{31}\color{orange}{w_{33}}\boldsymbol u_{3}&v_{12}\color{red}{w_{11}}\boldsymbol u_{1}+v_{22}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{32}\color{orange}{w_{33}}\boldsymbol u_{3}&v_{13}\color{red}{w_{11}}\boldsymbol u_{1}+v_{23}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{33}\color{orange}{w_{33}}\boldsymbol u_{3}
\end{array}
\right)
つまり
$\boldsymbol x_{1}=v_{11}\color{red}{w_{11}}\boldsymbol u_{1}+v_{21}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{31}\color{orange}{w_{33}}\boldsymbol u_{3}$
$\boldsymbol x_{2}=v_{12}\color{red}{w_{11}}\boldsymbol u_{1}+v_{22}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{32}\color{orange}{w_{33}}\boldsymbol u_{3}$
$\boldsymbol x_{3}=v_{13}\color{red}{w_{11}}\boldsymbol u_{1}+v_{23}\color{blue}{w_{22}}\boldsymbol u_{2}+v_{33}\color{orange}{w_{33}}\boldsymbol u_{3}$
となります。
$\boldsymbol x_{1}=v_{11}\underset{\large大きさ\small×\large方向}{\underline{\color{red}{w_{11}}\boldsymbol u_{1}}}+v_{21}\underline{\color{blue}{w_{22}}\boldsymbol u_{2}}+v_{31}\underline{\color{orange}{w_{33}}\boldsymbol u_{3}}$
ベクトル $\boldsymbol u$ は方向を示しており特異値$w_{11}$、$w_{22}$、$w_{33}$は $\boldsymbol u$ の大きさを示しているのがわかります。また、$\boldsymbol u$ は直交行列なので$\boldsymbol u_{1},\boldsymbol u_{2},\boldsymbol u_{3}$は直交しています。
$\boldsymbol x_{1},\boldsymbol x_{2},\boldsymbol x_{3}$をデータ点とみなすと特異値分解後のイメージは以下のようになります。特異値の大きさが違うので軸の長さも異なります。
特異値の大きさは$\color{red}{w_{11}}>\color{blue}{w_{22}}> \color{orange}{w_{33}}$となっています。
ここで1番小さい特異値を含んでいる軸 $\color{orange}{w_{33}}\boldsymbol u_{3}$ を削減してみます。$\color{orange}{w_{33}}=0$とすることで削減できます。以下に削減後の図を示します。
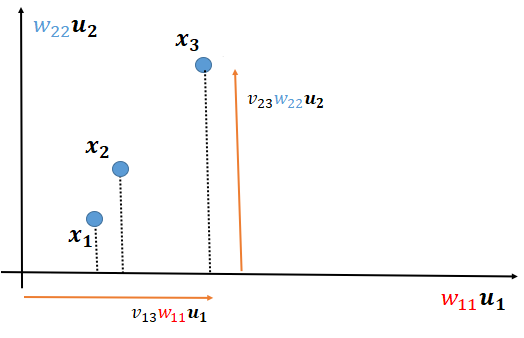
ここで注目してほしいのは $\boldsymbol x_{1},\boldsymbol x_{2},\boldsymbol x_{3}$ の位置関係です。$\color{orange}{w_{33}}\boldsymbol u_{3}$削減後も$\boldsymbol x_{1}$と$\boldsymbol x_{2}$の方が$\boldsymbol x_{2}$と$\boldsymbol x_{3}$よりも近いという特徴を保っています。このように影響力の小さい特異値を削減することで出来るだけデータの特徴を保ったまま近似することができます。
特異値分解による文書解析
ここでは、4つの文を特異値分解することで特異値分解によって何ができるのか説明していきます。
以下のような4つの文を考える。
文1:I write a letter
文2:I write a birthday card
文3:I go to school
文4:I went to school
私たち人間であれば、goとwentはほぼ同じ意味の単語であるとか、文1と文2は何となく同じだなぁ、というのがわかります。特異値分解を用いると、この似てるという感じを数字で表現することができます。つまり、コンピューターがこの文章や単語は似ていると判断できるようになります。それではこれらの文を特異値分解していきます。
4つの文はそのままだと計算できないので、以下のように行列で表現します。行列での表現方法は他にもありますが、今回は文書を単語の出現頻度で表現しています。
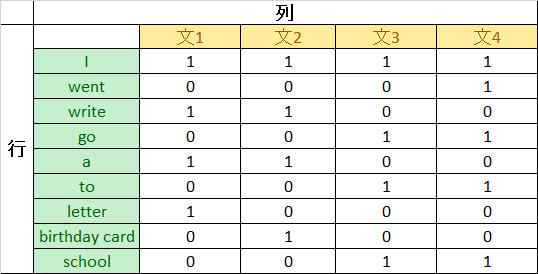
この行列は各文にそれぞれどの単語があるのかを示しています。例えば、birthday card は文2に出てくるので、2列目の8行目に1を入れています。これを行列Aとして数式で表現すると以下のようになります。
A =
\left(
\begin{array}{c}
1 & 1 & 1 &1 \\
0 & 0 & 0 & 1 \\
1 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
1 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
\end{array}
\right)
行列Aはただの数字に見えますが、行が単語、列が文を表していることを意識していてください。この行列Aを特異値分解すると以下のように$U$の行が単語、$V^T$の列が文を表しています。
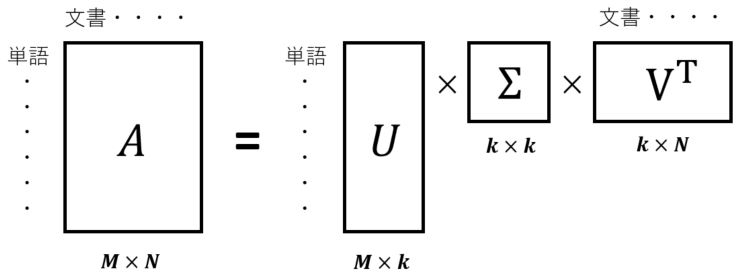
では実際に行列$A$を特異値分解してみます。以下に特異値分解の結果を示しています。
A =
\left(
\begin{array}{c}
1 & 1 & 1 &1 \\
0 & 0 & 0 & 1 \\
1 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
1 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
\end{array}
\right)
=
\left(
\begin{array}{c}
-0.6667 & 0.0000 & 0.0000 & 0.0966\\
-0.1667 & -0.2236 & 0.0621 & -0.9633\\
-0.3333 & 0.4472 & 0.0000 & -0.0426\\
-0.1667 & -0.2236 & 0.0000 & 0.1392\\
-0.3333 & 0.4472 & 0.0000 & -0.0426\\
-0.3333 & -0.4472 & 0.0000 & 0.1392\\
-0.1667 & 0.2236 & -0.7071 & -0.0213\\
-0.1667 & 0.2236 & 0.7071 & -0.0213\\
-0.3333 & -0.4472 & 0.0000 & 0.1392\\
\end{array}
\right)
×
\left(
\begin{array}{c}
3.1470 & 0.0000 & 0.0000 & 0.0000 \\
0.0000 & 2.372 & 0.0000 & 0.0000 \\
0.0000 & 0.0000 & 1.0000 & 0.0000\\
0.0000 & 0.0000 & 0.0000 & \color{red}{0.6828}\\
\end{array}
\right)
×
\left(
\begin{array}{c}
-0.4007 & -0.4007 & -0.5509 & -0.6127\\
0.5824 & 0.5824 & -0.3602 & -0.4380\\
-0.7071 & 0.7071 & 0.0000 & 0.0000\\
-0.0145 & -0.0145 & 0.7529 & -0.6578\\
\end{array}
\right)
数字が多くて分かりにくいですが$A = UΣV^T$の形になっています。
ここで注目して欲しいのは特異値です。真ん中の行列$\Sigma$の部分です。
4つの特異値は先ほども説明したように行列$A$の全ての要素に影響を与えています。
ここで4つの特異値のうち一番値が小さい特異値(赤色の数字)を削減してみます。
特異値削減後の行列を$A'$とすると$UΣV^T$の部分は以下のようになります。
A' =
\left(
\begin{array}{c}
-0.6667 & 0.0000 & 0.0000 \\
-0.1667 & -0.2236 & 0.0621 \\
-0.3333 & 0.4472 & 0.0000 \\
-0.1667 & -0.2236 & 0.0000 \\
-0.3333 & 0.4472 & 0.0000 \\
-0.3333 & -0.4472 & 0.0000 \\
-0.1667 & 0.2236 & -0.7044 \\
-0.1667 & 0.2236 & 0.7044 \\
-0.3333 & -0.4472 & 0.0000 \\
\end{array}
\right)
×
\left(
\begin{array}{c}
3.1470 & 0.0000 & 0.0000 \\
0.0000 & 2.2361 & 0.0000 \\
0.0000 & 0.0000 & 1.0000 \\
\end{array}
\right)
×
\left(
\begin{array}{c}
-0.5000 & -0.5000 & -0.5000 & -0.5000\\
0.5000 & 0.5000 & -0.5000 & -0.5000\\
-0.7044 & 0.7044 & 0.0621 & 0.0621\\
\end{array}
\right)
$A'$を計算すると以下の右側式のようになります。
特異値分解前の行列$A$と比較すると値が変化している部分があります。
A =
\begin{array}{c}
I\\
\color{red}{went}\\
write\\
\color{red}{go}\\
a\\
to\\
\color{blue}{letter}\\
\color{blue}{birthday card}\\
school\\
\end{array}
\left(
\begin{array}{c}
1 & 1 & 1 &1 \\
\color{red}0 & \color{red}0 & \color{red}0 & \color{red}1\\
1 & 1 & 0 & 0\\
\color{red}0 & \color{red}0 & \color{red}1 & \color{red}0\\
1 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
\color{blue}1 & \color{blue}0 & \color{blue}0 & \color{blue}0\\
\color{blue}0 & \color{blue}1 & \color{blue}0 & \color{blue}0\\
0 & 0 & 1 & 1\\
\end{array}
\right)
A'=
\left(
\begin{array}{c}
1.000 & 1.000 & 1.000 &1.000 \\
\color{red}{0.044} & \color{red}{-0.044} & \color{red}{0.496} & \color{red}{0.504} \\
1.000 & 1.000 & 0.000 & 0.000\\
\color{red}{-0.044} & \color{red}{0.044} & \color{red}{0.504}& \color{red}{0.496}\\
1.000 & 1.000 & 0.000 & 0.000\\
0.000 & 0.000 & 1.000 & 1.000\\
\color{blue}{0.996} & \color{blue}{0.004} & \color{blue}{-0.044} & \color{blue}{0.044}\\
\color{blue}{0.004} & \color{blue}{0.996} & \color{blue}{0.044} & \color{blue}{-0.044}\\
0.000 & 0.000 & 1.000 & 1.000\\
\end{array}
\right)
(上式の赤色と青色の文字と数字は後程使うので意識していて下さい)
ここで単語の類似度を計算してみます。計算対象はwentとgo、letterとbirthdaycardです。この単語2組がどれほど似ているのか計算します。
今回類似度計算にはコサイン類似度を用います。詳細は省略しますが、$\cos$類似度は以下の式になります。
\vec{a}=(a_{1},a_{2},...,a_{n})
\vec{b}= (b_{1},b_{2},...,b_{n})
ベクトル $\vec{a},\vec{b}$ のコサイン類似度式は以下です。
\cos(\vec{a},\vec{b})=\displaystyle\frac{a_{1}b_{1}+...+a_{n}b_{n}}{\sqrt{{a_{1}^{2}+...+a_{n}^{2}}}\sqrt{{b_{1}^{2}+...+b_{n}^{2}}}}
コサイン類似度は0~1の値をとり、1に近づくほど2つベクトルが似ていることを示しています。
ではさっそくコサイン類似度を計算してみます。wentとgo、letterとbirthdaycardの単語の類似度を計算します。もちろん単語そのものでは計算できないので、単語のベクトルを取り出します。4つの単語のベクトルを取り出すと以下のようになります。ちょうどwent,goは赤のラインのベクトルを取り出し、letterとbirthdaycardは青色のベクトルを取り出しています。以下では分かりやすいように、単語にベクトル記号を付けています。
特異値分解前
\left\{
\begin{aligned}
&\vec{went} = (0 0 0 1) \vec{go}= (0 0 1 0)\\
&\vec{letter} = (1 0 0 0) \vec{birthdaycard}= (0 1 0 0)\\
\end{aligned}
\right.
ではコサイン類似度を計算します。
\cos類似度
\left\{
\begin{aligned}
&\cos(\vec{went},\vec{go})=0\\
&\cos(\vec{letter},\vec{birthdaycard})=0\\
\end{aligned}
\right.
結果は2つともコサイン類似度0になります。よってこの2つの単語組は全く似ていないということです。次に特異値を1つ消した行列のコサイン類似度を計算します。行列$A'$から取り出します。
特異値削減後
\left\{
\begin{aligned}
&\vec{went} = (0.044 -0.044 0.496 0.504) \vec{go}= (-0.044 0.044 0.504 0.496)\\
&\vec{letter} = (0.996 0.004 -0.044 0.044) \vec{birthdaycard}= (0.004 0.996 0.044 -0.044)\\
\end{aligned}
\right.
\cos類似度
\left\{
\begin{aligned}
&\cos(\vec{went},\vec{go})=0.9845\\
&\cos(\vec{letter},\vec{birthdaycard})=0.0041\\
\end{aligned}
\right.
wentとgoのコサイン類似度が1に近い値になっています。つまり、特異値を1つ削ることで、wentとgoがほぼ同じ意味の単語とみなすことができました。letterとbirthdaycardのコサイン類似度も0から0.0041に変化し、類似度が少し近づいたことが分かります。
ではさらに特異値を削減してみます。削減後の行列を$A''$とします。
A''=
\left(
\begin{array}{c}
-0.6667 & 0.0000 & \\
-0.1667 & -0.2236 & \\
-0.3333 & 0.4472 & \\
-0.1667 & -0.2236 & \\
-0.3333 & 0.4472 & \\
-0.3333 & -0.4472 & \\
-0.1667 & 0.2236 & \\
-0.1667 & 0.2236 & \\
-0.3333 & -0.4472 & \\
\end{array}
\right)
×
\left(
\begin{array}{c}
3.1470 & 0.0000 \\
0.0000 & 2.2361 \\
\end{array}
\right)
×
\left(
\begin{array}{c}
-0.5000 & -0.5000 & -0.5000 & -0.5000\\
0.5000 & 0.5000 & -0.5000 & -0.5000\\
\end{array}
\right)
行列$A''$を計算すると以下になります。
A’’=
\begin{array}{c}
I\\
\color{red}{went}\\
write\\
\color{red}{go}\\
a\\
to\\
\color{blue}{letter}\\
\color{blue}{birthday card}\\
school\\
\end{array}
\left(
\begin{array}{c}
1 & 1 & 1 &1 \\
\color{red}0 & \color{red}0 & \color{red}{0.5} & \color{red}{0.5}\\
1 & 1 & 0 & 0\\
\color{red}0 & \color{red}0 & \color{red}{0.5} & \color{red}{0.5}\\
1 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
\color{blue}{0.5} & \color{blue}{0.5} & \color{blue}0 & \color{blue}0\\
\color{blue}{0.5} & \color{blue}{0.5} & \color{blue}0 & \color{blue}0\\
0 & 0 & 1 & 1\\
\end{array}
\right)
goとwent、letterとbirthdaycardが同じ値のベクトルになっています。
コサイン類似度はこのようになります。
$\cos(\vec{went},\vec{go})=0.9999...$
$\cos(\vec{letter},\vec{birthdaycard})=0.9999...$
このように特異値を削減することによって、goとwent、letterとbirthdaycardが同じ単語とみなすことができました。
これは行列$A$に与える影響力の小さい特異値を削減することで、似たような意味の単語を1つのベクトルに集約していると言えます。例えば、「サッカー」や「野球」といった単語はスポーツという広い意味をもっているものに集約されます。行列$A''$は単語の比較だけでなく文の比較も可能です。以下の式のように列で比較すると文1と文2、文3と文4が同じものになっています。これは4つの文を2つに分類できたと言えます。特異値分解の応用例としてLSI(Latent Semantic Indexing)があるのですが、LSIでは文書の単語を解析し、その文書を複数のカテゴリに分類することができます。
文1 文2 文3 文4
\left(
\begin{array}{c}
\color{LimeGreen}1 & \color{LimeGreen}1 & \color{orange}1 &\color{Orange}1 \\
\color{LimeGreen}0 & \color{LimeGreen}0 & \color{orange}{0.5} &\color{orange}{0.5}\\
\color{LimeGreen}1 & \color{LimeGreen}1 & \color{orange}0 & \color{orange}0\\
\color{LimeGreen}0 & \color{LimeGreen}0 & \color{orange}{0.5} & \color{orange}{0.5}\\
\color{LimeGreen}1 & \color{LimeGreen}1 &\color{orange} 0 & \color{orange}0\\
\color{LimeGreen}0 & \color{LimeGreen}0 & \color{orange}1 & \color{orange}1\\
\color{LimeGreen}{0.5} & \color{LimeGreen}{0.5} & \color{orange}0 & \color{orange}0\\
\color{LimeGreen}{0.5} & \color{LimeGreen}{0.5} & \color{orange}0 & \color{orange}0\\
\color{LimeGreen}0 & \color{LimeGreen}0 & \color{orange}1 & \color{orange}1\\
\end{array}
\right)
特異値分解計算方法
ここでは特異値分解の計算方法を説明していきます。
$A=UΣV^T$の$U,Σ,V^T$の求め方を示していきます。
目標としては以下を埋める感じです。
$U=$
$V=$
$Σ=$
まず$A^T=VΣU^T$となります。下図を見ると明らかです。

ここで
$AA^T=(UΣV^T)(VΣU^T)=UΣ^2U^T$
$A^TA=(VΣU^T)(UΣV^T)=VΣ^2V^T$
また、$AA^T=A'$ $,$ $Σ^2=Λ$とおくと
$AA^T=A'=UΛU^T$
ここで固有値について考えます。
正方行列$A$ スカラー$λ$ ベクトル$\vec{x}$(0ベクトル以外)に対して以下が成り立つとき
$A\vec{x}=λ\vec{x}$
このとき$\vec{x}$を$A$の固有ベクトルという。($λ$を$A$の固有値という)
ここで
Λ =
\left(
\begin{array}{c}
λ_{1}&&\\
&λ_{2}&&\\
&&&\ddots\\
\end{array}
\right)
$U=(\vec{x_{1}} \vec{x_{2}} \vec{x_{3}} ・・・)$
と置くと $A\vec{x}=λ\vec{x}$ は
$AU=UΛ$
となり、左から$U^{-1}$をかけて
$A=UΛU^{-1}$
となります。また、特異値分解での$U$は直行行列なので、$U^T=U^{-1}$となります。
$A=UΛU^{-1}=UΛU^T$
ここで$\vec{x}$を$A$の固有ベクトルというのでした。$\vec{x}=U$なので、$U$は$A$の固有ベクトルなのです。
では、話を戻します。
$AA^T=A'=UΛU^T$
より、$A'$の固有ベクトルを求めると$U$が求まります。同じように$V$は$A^TA$の固有ベクトルを求めることで分かります。また、$Λ$は$A'$の固有値です。
以上から特異値分解$A=UΣV^T$は
$U=AA^T$の固有ベクトル
$V=A^TA$の固有ベクトル
$Σ=AA^T$の固有値の平方($A^TA$の固有値でも可)
以上を計算することで求まります。よってプログラムで特異値分解をする場合は上の計算をすれば求まります。
参考文献
pythonで特異値分解(SVD)を理解する
https://ohke.hateblo.jp/entry/2017/12/14/230500