Python + Tkinter - 統計的な調査に要する標本サイズを算出するアプリ

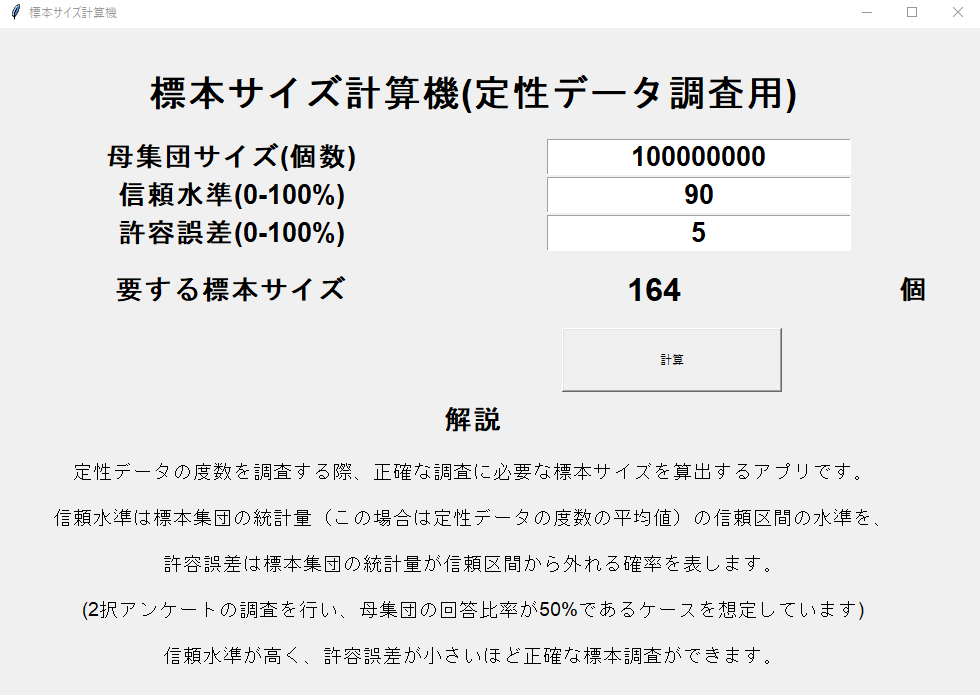
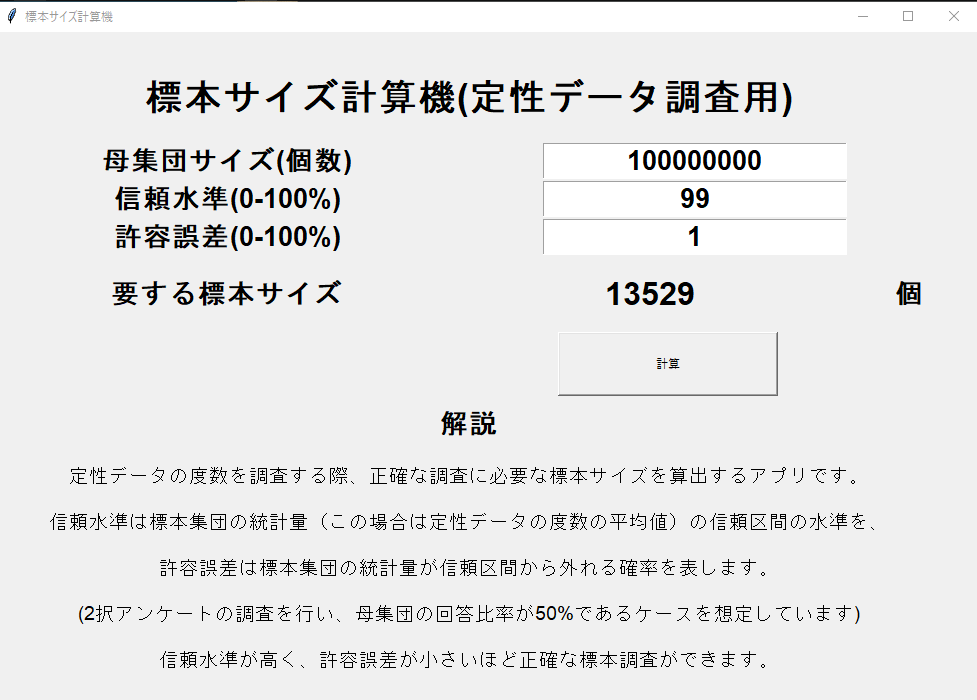
Tkinter学習の一環で統計的な調査に必要なサンプル数を算出するアプリを作ってみました。「統計WEB」の母比率の区間推定における必要なサンプルサイズの解説ページを参考に制作しました。

コード

from tkinter import *
from tkinter import font
from scipy.stats import norm

#ウィンドウのタイトル+サイズ
window = Tk()
window.title("標本サイズ計算機")
window.minsize(width=600, height=450)
window.config(padx=50, pady=20)

myfont = font.Font(family='Helvetica', size=20, weight='bold')
myfont_result = font.Font(family='Helvetica', size=24, weight='bold')
myfont_h1 = font.Font(family='Helvetica', size=28, weight='bold')
myfont_p = font.Font(family='Helvetica', size=14, weight='normal')

def calculate_samplesize():
    n_value = float(n_input.get())
    z_value = float(float(z_input.get()) / 100)
    e_value = float(float(e_input.get()) / 100)

    #母集団の回答比率が50%である場合の標準誤差
    std_value = 0.25
    #標準正規分布のz値の累積分布関数の逆値を求める
    z_invert = float(norm.ppf(z_value, 0, 1))

    print(z_invert)

    samplesize = ((z_invert**2) * std_value / (e_value**2)) / 1 + ((z_invert**2) * std_value / (e_value * n_value))
    samplesize = int(samplesize)

    print(samplesize)

    s_result_label.config(text=f"{samplesize}")


#タイトル
title_label = Label(text="標本サイズ計算機(定性データ調査用)", font=myfont_h1)
title_label.grid(column=0, row=0, columnspan=3, pady=20)

#母集団サイズを入力
n_label = Label(text="母集団サイズ(個数)", font=myfont,padx=10)
n_label.grid(column=0, row=1)

n_input = Entry(width=20, font=myfont, justify=CENTER)
n_input.grid(column=2, row=1)


#信頼水準を入力
z_label = Label(text="信頼水準(0-100%)", font=myfont,padx=10)
z_label.grid(column=0, row=2)

z_input = Entry(width=20, font=myfont, justify=CENTER)
z_input.grid(column=2, row=2)


#許容誤差を入力
e_label = Label(text="許容誤差(0-100%)", font=myfont,padx=10)
e_label.grid(column=0, row=3)

e_input = Entry(width=20, font=myfont, justify=CENTER)
e_input.grid(column=2, row=3)

#標本サイズへの換算値
s_label = Label(text="要する標本サイズ", font=myfont)
s_label .grid(column=0, row=4)

s_result_label = Label(text="0",font=myfont_result)
s_result_label.grid(column=1, row=4,columnspan=2)

s_label = Label(text="個", font=myfont, pady=20)
s_label.grid(column=3, row=4)

#ボタンで算出
calculate_button = Button(text="計算",command=calculate_samplesize, width=30, height=3, pady=5)
calculate_button.grid(column=1, row=5, columnspan=3)

p1_label = Label(text="解説", font=myfont, pady=10)
p1_label.grid(column=0, row=6, columnspan=3)

p2_label = Label(text="定性データの度数を調査する際、正確な調査に必要な標本サイズを算出するアプリです。", font=myfont_p, pady=10)
p2_label.grid(column=0, row=7, columnspan=3)

p3_label = Label(text="信頼水準は標本集団の統計量（この場合は定性データの度数の平均値）の信頼区間の水準を、", font=myfont_p, pady=10)
p3_label.grid(column=0, row=8, columnspan=3)

p4_label = Label(text="許容誤差は標本集団の統計量が信頼区間から外れる確率を表します。", font=myfont_p, pady=10)
p4_label.grid(column=0, row=9, columnspan=3)

p4_label = Label(text="(2択アンケートの調査を行い、母集団の回答比率が50%であるケースを想定しています)", font=myfont_p, pady=10)
p4_label.grid(column=0, row=10, columnspan=3)

p4_label = Label(text="信頼水準が高く、許容誤差が小さいほど正確な標本調査ができます。", font=myfont_p, pady=10)
p4_label.grid(column=0, row=11, columnspan=3)

#定性データの度数を調査する際、正確な調査に必要な標本サイズを算出するアプリです。
#信頼水準は標本集団の統計量（この場合は定性データの度数の平均値）の信頼区間の水準を、
#許容誤差は標本集団の統計量が信頼区間から外れる確率を表します。
#(2択アンケートの調査を行い、母集団の回答比率が50%であるケースを想定しています)

#メインループを実行
window.mainloop()

要する標本サイズを実際に計算してみると、許容誤差が5%ほどの場合は標本サイズが100-10000程で正確な調査ができることが分かります。信頼水準を99%、許容誤差が1%以下となるとそれ以上に標本数を増やす必要があります。