Matlabを使った倒立2輪ロボットの安定化
Self-Balancing Robotの制御を実装するため,文献「倒立二輪ロボット(モータ1軸)の安定化と走行制御」をMatlabでなぞってみました.
プログラムへの落とし込み
文献内「2.倒立二輪ロボットの概略とモデリング」と同じパラメータを使い,「3.倒立二輪ロボットの安定化」にある状態方程式をプログラムにします.
ここで,下記のように2点の修正を行いました.
1.ゲインa[Nm/A]についての表記がありませんでしたので,結果の逆算から
a = トルク定数Kt × ギヤ比i × 減速機効率75%
とする事にしました.
2.また,状態方程式のまとめ部分を下記のように修正します.
\begin{equation}
\frac{d}{dt}
\begin{bmatrix}
θ\\
φ\\
\dot{θ}\\
\dot{φ}
\end{bmatrix}
=
\begin{bmatrix}
0_{2×2} &I_{2×2} \\
-α^{-1}γ &-α^{-1}β\\
\end{bmatrix}
\begin{bmatrix}
θ\\
φ\\
\dot{θ}\\
\dot{φ}
\end{bmatrix}
+
\begin{bmatrix}
0_{2×2}\\
-α^{-1}δ
\end{bmatrix}
u
\end{equation}
ここで,この式にまとめる際にδuは移項されないため-αとならず,
また,0マトリクスはδのベクトルに合わせる必要があるため,2×2ではなく,
\begin{equation}
\frac{d}{dt}
\begin{bmatrix}
θ\\
φ\\
\dot{θ}\\
\dot{φ}
\end{bmatrix}
=
\begin{bmatrix}
0_{2×2} &I_{2×2} \\
-α^{-1}γ &-α^{-1}β\\
\end{bmatrix}
\begin{bmatrix}
θ\\
φ\\
\dot{θ}\\
\dot{φ}
\end{bmatrix}
+
\begin{bmatrix}
0_{2×1}\\
α^{-1}δ
\end{bmatrix}
u
\end{equation}
となります.
プログラム
これらをMatlabプログラムに表すと下記のようになります.
(このプログラムを実行するには,ControlSystemToolboxが必要です.)
m=0.686 %kg
M=0.0605 %kg
Jp=0.00316 %kg m^2
Jt= 0.00000535 %kg m^2
Jm=0.00000013 %kg m^2
l=0.148 %m
r=0.02 %m
c=0.0001 %kgm^2/s
K = 0.00279 %Nm/A
i = 30
a = K * i * 0.75
g=9.81 %m/s^2
alpha11 = (M+m)*r^2 + m*l*r + Jt + i*Jm
alpha12 = (M+m)*r^2 + Jt + i^2*Jm
alpha21 = (M+m)*r^2 + 2*m*l*r + m*l^2 + Jp + Jt + Jm
alpha22 = (M+m)*r^2 + m*l*r + Jt + i*Jm
alpha=[alpha11,alpha12;alpha21,alpha22]
beta = [0,c;0,0]
gamma = [0,0;-m*g*l,0]
delta = [a;0]
I = eye(2)
O22 = zeros(2)
O21 = zeros(2,1)
A = [O22,I;-(alpha^-1)*gamma,-(alpha^-1)*beta]
B = [O21;(alpha^-1)*delta]
Q = [1,0,0,0;0,1,0,0;0,0,1,0;0,0,0,1]
R=500
[K,S,e] = lqr(A,B,Q,R)
実行結果
上記のプログラムを実行した結果
K =
-11.7357 -0.0447 -1.4987 -0.0638
S =
1.0e+03 *
3.9639 0.0335 0.5610 0.0415
0.0335 0.0014 0.0051 0.0005
0.5610 0.0051 0.0815 0.0063
0.0415 0.0005 0.0063 0.0006
e =
-19.3440
-7.9842
-4.4475
-1.0114
となりました.文献内では
K= [-11.7400 -0.0447 -1.4994 -0.0638]
に対して
K= [-11.7357 -0.0447 -1.4987 -0.0638]
と誤差がある結果になりました.
おそらくaやgなど明記されていないパラメータの誤差だと考えられます.
制御シミュレーション
ここで得られたゲインKを用いて,
u(t)=-Kx(t)
となるように実行する事で,ロボットが倒立できるはずです.
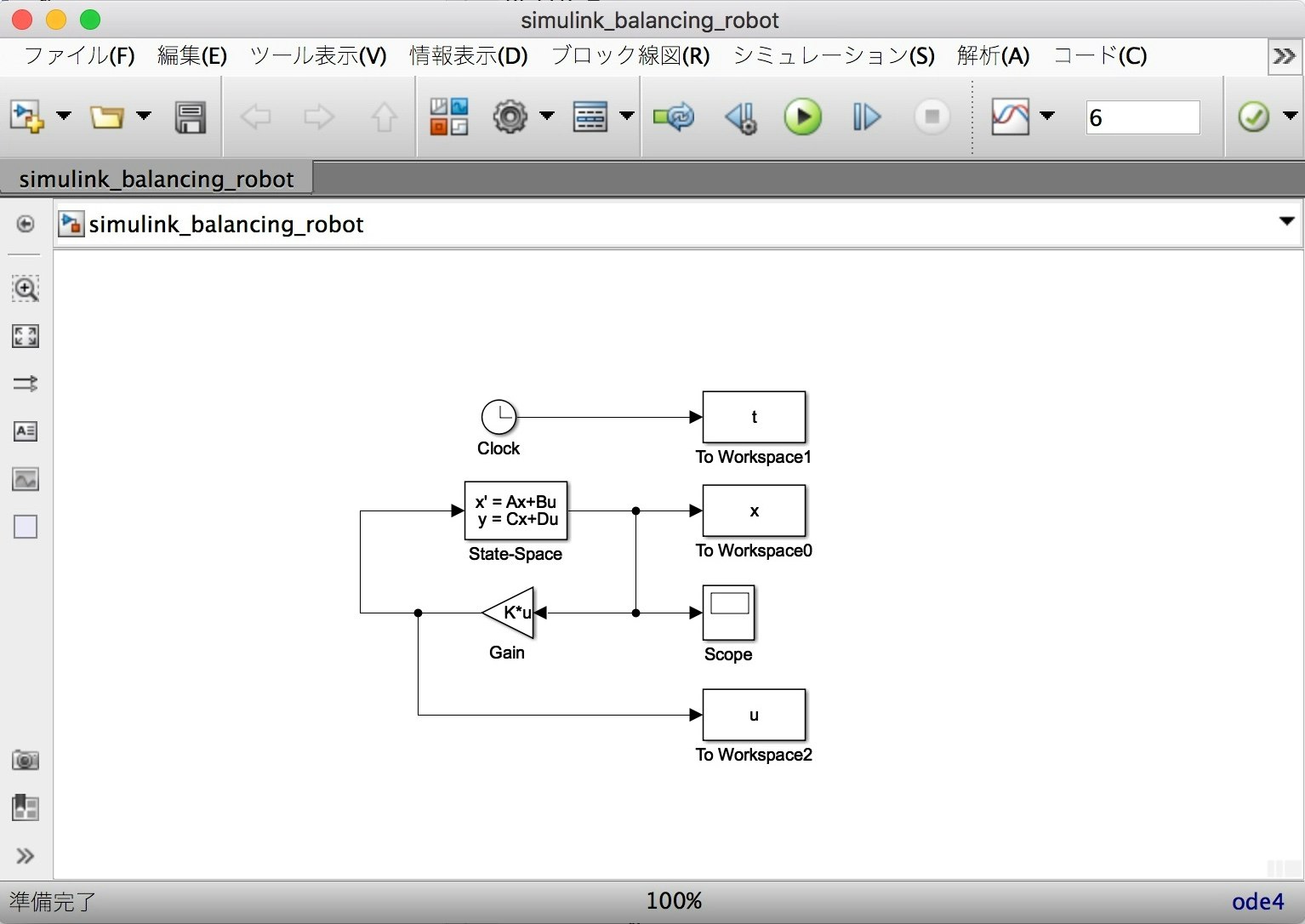
これをsimulinkモデルで記述し,シミュレーションを実行します.
前かがみ5°の位置にした状態でスタートするように,初期値を
x0 = [5*pi/180;0;0;0]
としました.
それぞれのモデル内は下記の図のように設定します.シミュレーション時間は6sです.
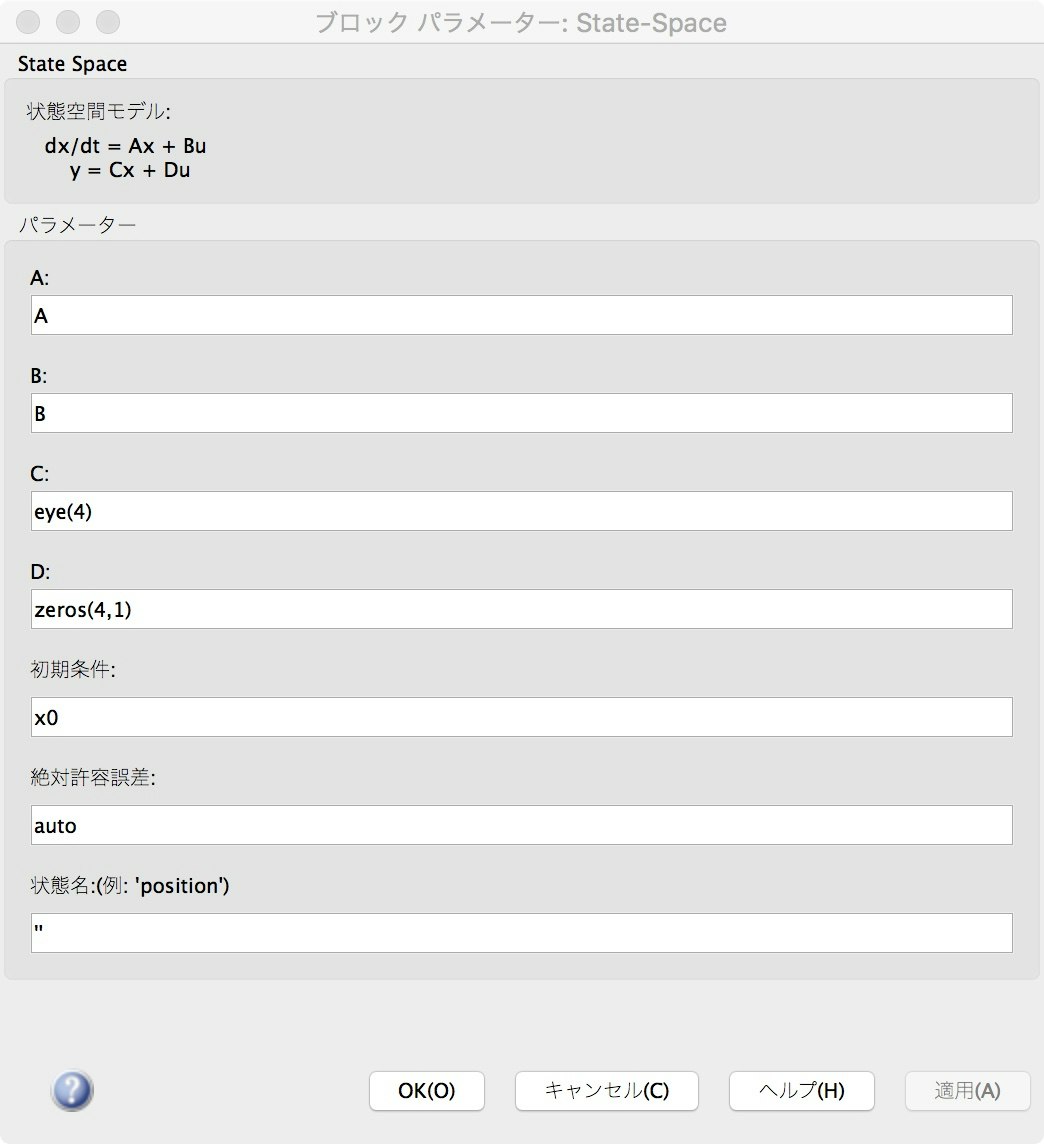
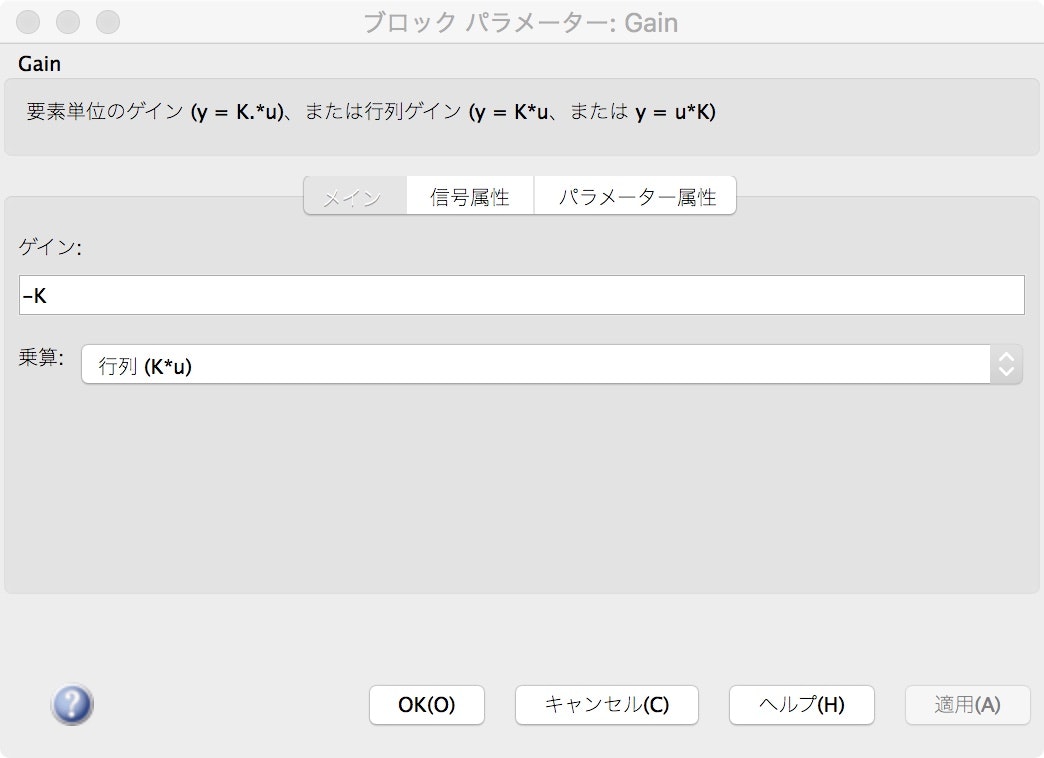
ここで再生ボタンで実行する事で,t,x,uが変数として結果が出力されます.
これらをグラフで出力した結果が下記になります.
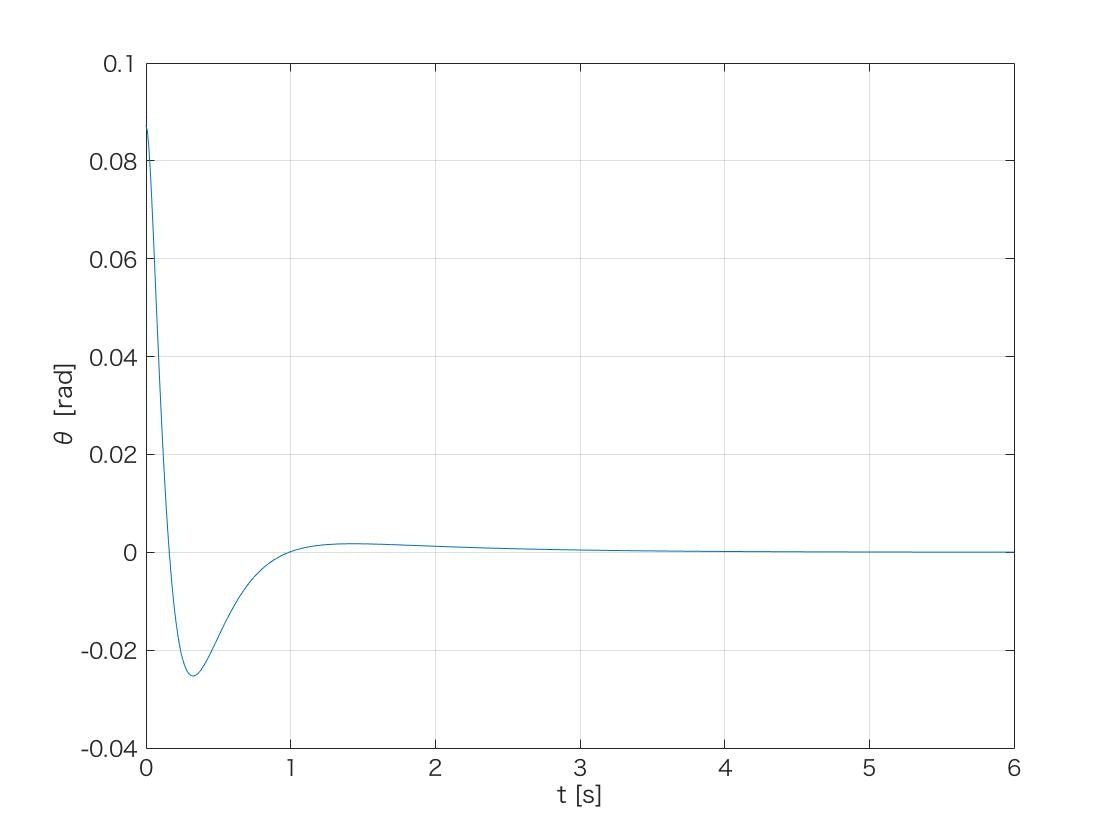
ロボットの姿勢θは,一度反対方向に倒れてから3sほどで直立になっています.
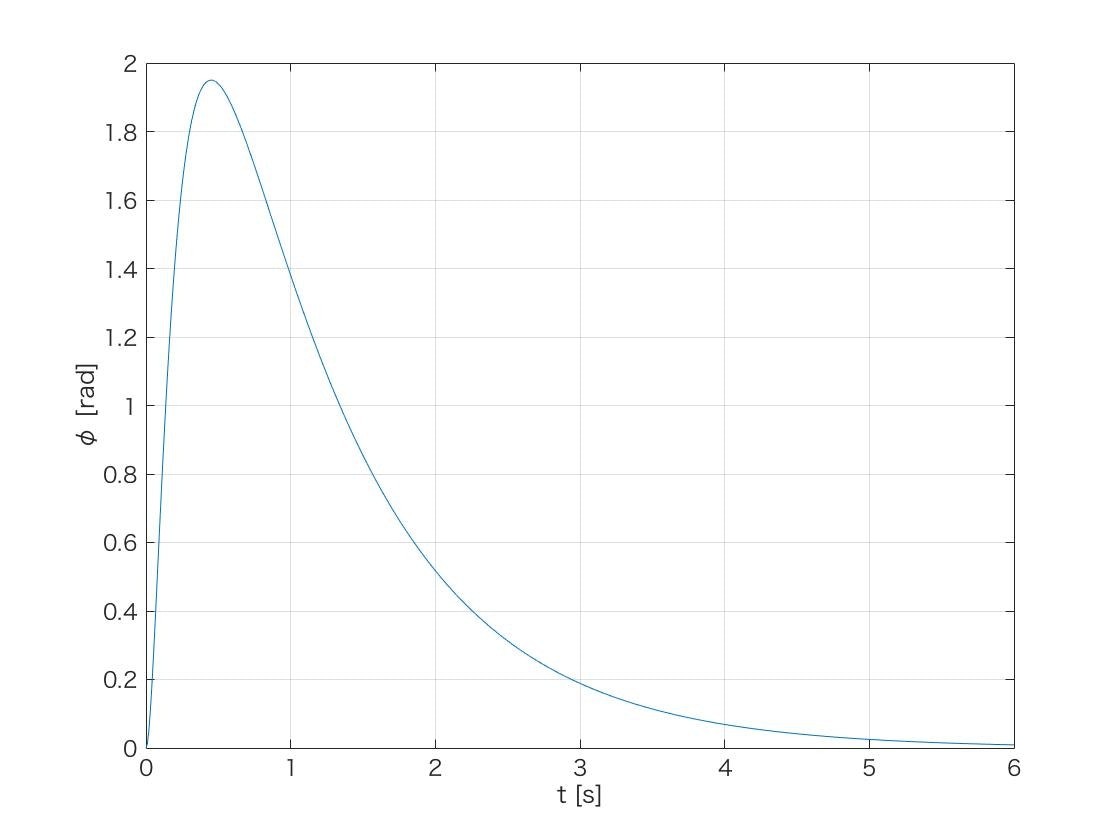
タイヤの角度は,6sほどかけてゆっくり初期位置に戻っています.
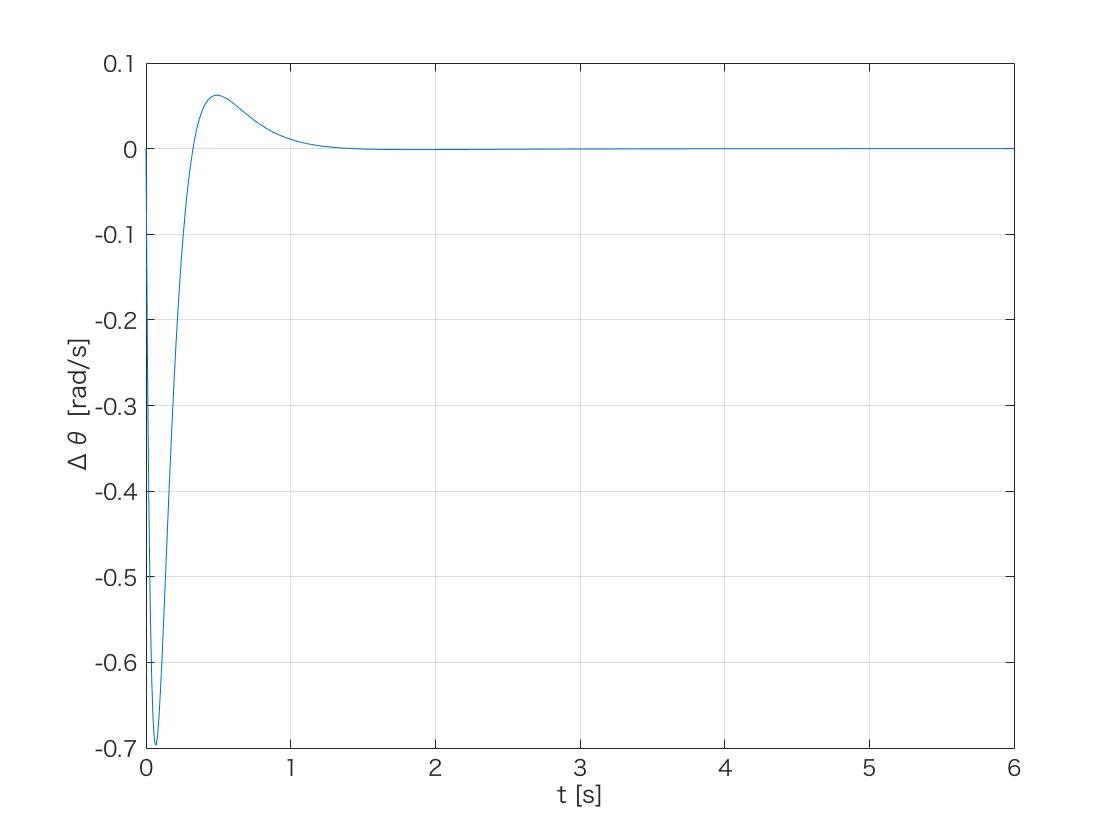
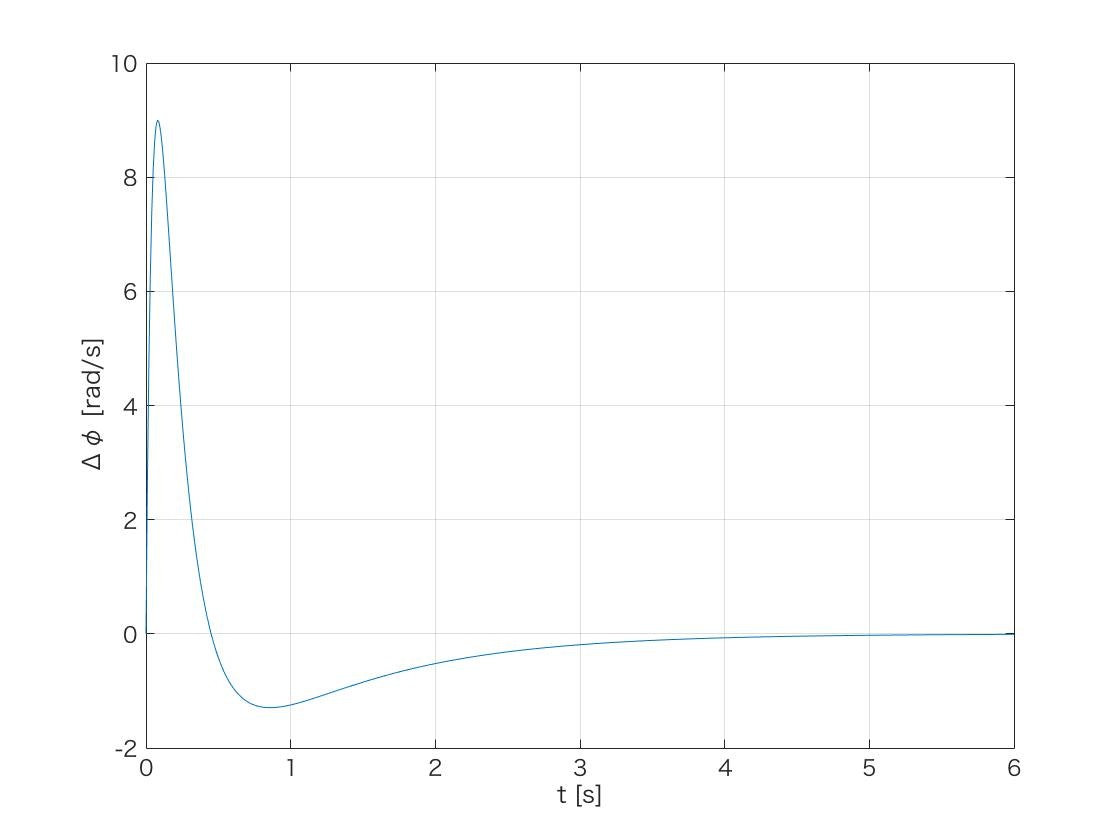
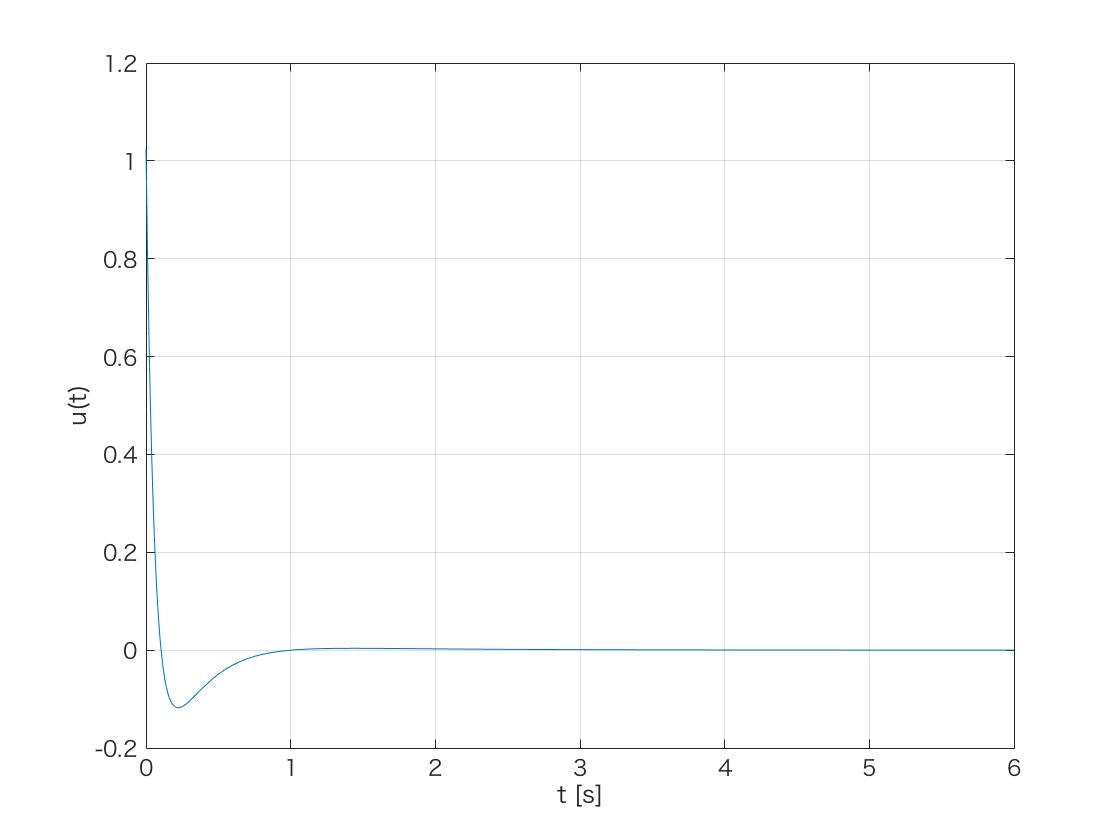
もっと早く収束させるためには,文献の通り重み行列Qを変更する事で,ゲインを高くし応答性を上げれらます.
ただし,必要なu(t)が大きくなっていきますので,モータの限界出力を超えない範囲で考える必要があるようです.
まとめ
これで倒立2輪の一通りの計算過程がわかりましたので,そのうち実機で試してみたいと思います.