はじめに
条件さえ揃えば、普通のカメラ(RGBカメラ)でも、長さを測れるのでは?という素朴な疑問が生じたので調べてみた。
具体的には、
【条件】3辺の長さが分かっている三角形がある
↓
【測定】その3点が張る平面上にある点間の距離が分かる。
先に、結果を知りたい方は、こちらをクリック!
条件
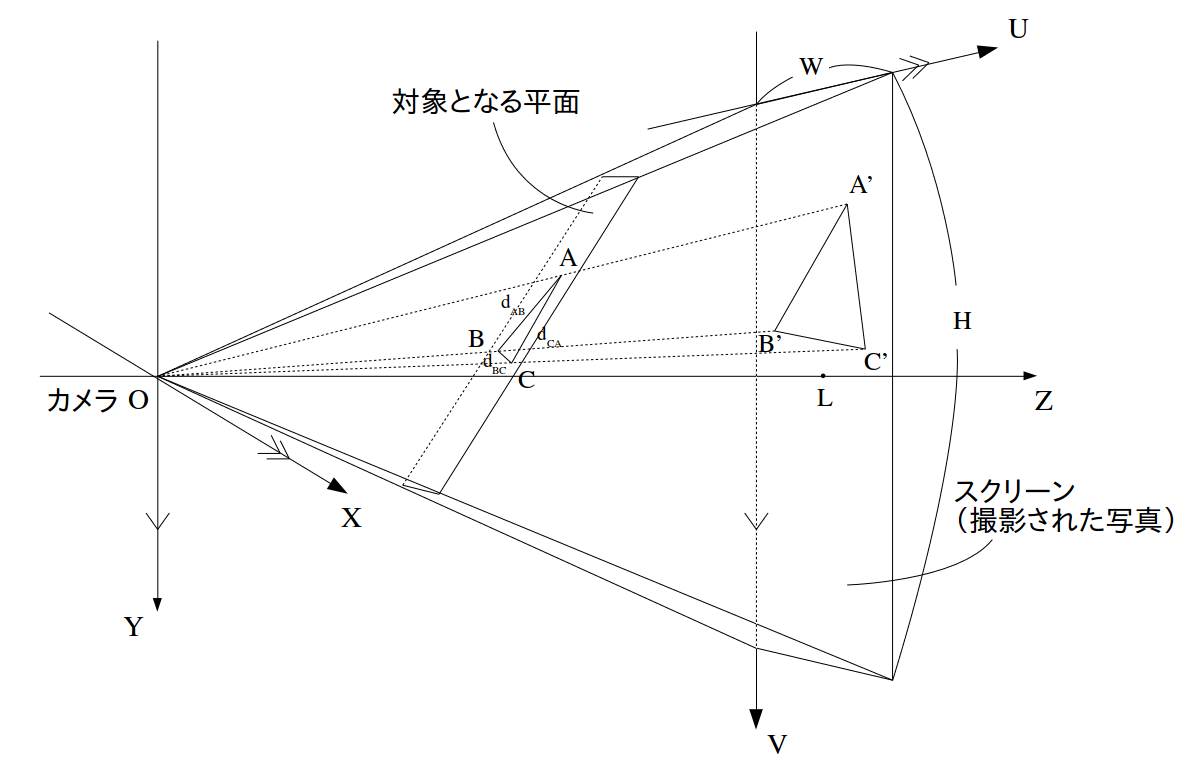
- スクリーン(写真)の高さ: $\rm{H}$
- スクリーン(写真)の幅: $\rm{W}$
- 垂直画角: $\rm\theta_{v}$(カメラのスペック要確認)
- 水平画角: $\rm\theta_{h}$(カメラのスペック要確認)
- スクリーンまでの距離: $\rm L$ ($ = \frac{\rm H}{2 \tan \frac{\theta_{v}}{2}} = \frac{\rm W}{2 \tan \frac{\theta_{h}}{2}}$)
- $\rm{A}$の写真上の座標: $(\rm U_A, \rm V_A)$ ➔ 3次元座標: $A'=(\rm U_A - \frac{W}{2}, \rm V_A - \frac{H}{2}, L)$
- $\rm{B}$の写真上の座標: $(\rm U_B, \rm V_B)$ ➔ 3次元座標: $B'=(\rm U_B - \frac{W}{2}, \rm V_B - \frac{H}{2}, L)$
- $\rm{C}$の写真上の座標: $(\rm U_C, \rm V_C)$ ➔ 3次元座標: $C'=(\rm U_C - \frac{W}{2}, \rm V_C - \frac{H}{2}, L)$
3点 A,B,C の3次元座標を求める
3辺の長さが分かっているので、以下の条件を与える。
\begin{equation}
\left\{
\begin{aligned}
\bigr| \vec{AB} \bigl| & = d_{AB} \\
\bigr| \vec{BC} \bigl| & = d_{BC} \\
\bigr| \vec{CA} \bigl| & = d_{CA}
\end{aligned}
\right.
\end{equation}
ただし、
\begin{equation}
\begin{aligned}
&\vec{OA} = k \cdot \vec{e_A} \\
&\vec{OB} = l \cdot \vec{e_B} \\
&\vec{OC} = m \cdot \vec{e_C} \\
\vec{e_A} = \frac{\vec{OA'}}{\bigl|\vec{OA'}\bigr|},\,\,&
\vec{e_B} = \frac{\vec{OB'}}{\bigl|\vec{OB'}\bigr|},\,\,
\vec{e_C} = \frac{\vec{OC'}}{\bigl|\vec{OC'}\bigr|} \\
&k, l, m > 0
\end{aligned}
\end{equation}
これらを解くと、
\begin{equation}
\begin{aligned}
&\left\{
\begin{aligned}
\bigr| \vec{AB} \bigl| & = d_{AB} \\
\bigr| \vec{BC} \bigl| & = d_{BC} \\
\bigr| \vec{CA} \bigl| & = d_{CA}
\end{aligned}
\right.
\\
\Longleftrightarrow
&\left\{
\begin{aligned}
\bigr| \vec{AB} \bigl|^2 & = d_{AB}^2 \\
\bigr| \vec{BC} \bigl|^2 & = d_{BC}^2 \\
\bigr| \vec{CA} \bigl|^2 & = d_{CA}^2
\end{aligned}
\right.
\\
\Longleftrightarrow
&\left\{
\begin{aligned}
k^2 - &2\,kl\,\vec{OA}\cdot\vec{OB} + l^2 = d_{AB}^2 \\
l^2 - &2\,lm\,\vec{OB}\cdot\vec{OC} + m^2 = d_{BC}^2 \\
m^2 - &2\,mk\,\vec{OC}\cdot\vec{OA} + k^2 = d_{CA}^2 \\
\end{aligned}
\right.
\\
\Longleftrightarrow
&\left\{
\begin{aligned}
k^2 - &2\,kl\,\cos{\theta_{AB}} + l^2 = d_{AB}^2 \\
l^2 - &2\,lm\,cos{\theta_{BC}} + m^2 = d_{BC}^2 \\
m^2 - &2\,mk\,cos{\theta_{CA}} + k^2 = d_{CA}^2
\end{aligned}
\right.
\end{aligned}
\end{equation}
ただし、
\cos{\theta_{AB}} = \vec{e}_{A} \cdot \vec{e}_{B} \\
\cos{\theta_{BC}} = \vec{e}_{B} \cdot \vec{e}_{C} \\
\cos{\theta_{CA}} = \vec{e}_{C} \cdot \vec{e}_{A}
さらに整理すると、
\begin{equation}
\left\{
\begin{aligned}
k &= l \cos{\theta_{AB}} \pm \sqrt {d_{AB}^2 - l^2 \sin^2{\theta_{AB}}} \\
m &= l \cos{\theta_{BC}} \pm \sqrt {d_{BC}^2 - l^2 \sin^2{\theta_{BC}}} \\
2l^2-2kl\cos{\theta_{AB}}-&2lm\cos{\theta_{BC}}+2mk\cos{\theta_{CA}}-(d_{AB}^2 + d_{BC}^2 + d_{CA}^2) = 0 \\
0 & < l < \frac{d_{AB}}{\sin{\theta_{AB}}} \\
0 & < l < \frac{d_{BC}}{\sin{\theta_{BC}}}
\end{aligned}
\right. \tag{1}
\end{equation}
と書ける。
以上の条件を同時に満たす $(k,l,m)$ の組み合わせを見つける。
ここで、次のような関数 $f(l)$ を定義する。
f(l) = 2l^2-2k(l)l\cos{\theta_{AB}}-2lm(l)\cos{\theta_{BC}}+2m(l)k(l)\cos{\theta_{CA}}-(d_{AB}^2 + d_{BC}^2 + d_{CA}^2) \\
\begin{aligned}
\text{Subjected to} \,\,\,\, k(l) &= l \cos{\theta_{AB}} \pm \sqrt {d_{AB}^2 - l^2 \sin^2{\theta_{AB}}} \\
m(l) &= l \cos{\theta_{BC}} \pm \sqrt {d_{BC}^2 - l^2 \sin^2{\theta_{BC}}} \\
0 & < l < \min\Bigl\{\frac{d_{AB}}{\sin{\theta_{AB}}},\, \frac{d_{BC}}{\sin{\theta_{BC}}} \Bigr\}
\end{aligned}
$f(l) = 0$ を満たすような $l$ を求めたあと、(1)より、$k,m$ を求めれば、 $A,B,C$ それぞれの3次元空間の位置を求めることができる。
結果
左側から撮影
左の図は、ある一辺の長さを基準にして、他辺の長さを測った結果。(差分=推定値ー手採寸の値)
右の図は、本記事で提案した手法で計算した結果。数%の誤差(絶対寸法だと数ミリ程度)の精度を出せた...!!!


右側から撮影
左の図は、ある一辺の長さを基準にして、他辺の長さを測った結果。(差分=推定値ー手採寸の値)
右の図は、本記事で提案した手法で計算した結果。こちらも数%の誤差(絶対寸法だと数ミリ程度)の精度を出せた...!!!


まとめ
斜めから撮影した写真でも、ほぼ正確に寸法を推定できることが分かった!!
おわりに
ヒトやモノをデータ化&解析してみたい、という方。
3D技術と深層学習を組み合わせて、何か面白いサービスを作ってみたい!、という方。
弊社では一緒に働いてくれる仲間を大募集しています。
ご興味がある方は下記リンクから是非ご応募ください!
https://about.sapeet.com/recruit/