はじめに
量子化学計算(Psi4)の結果を加えることで、分子の物性予測を行う機械学習の機能向上を検討しました。
主な流れ
1.量子化学計算ソフトウェアであるPsi4による波動関数(wavefunction)の計算
2.wavefunctionからエネルギーなどの分子の物性に関する値を抽出し、およびSDFファイルへの出力
3.Fingerprintと上記の2で計算したパラメータを特徴量とした機械学習ライブラリのscikit-learnによる予測モデルの構築
4.Fingerprintのみの結果と3の結果の比較と評価
5.pytorchを使ったグラフニューラルネットワーク(GNN)での実装
6.まとめ・感想
1.wavefunctionの計算
1.1 学習データの準備
今回は学習データとしては分子が遺伝子に突然変異を引き起こす力を調べた結果であるAmes試験データと水溶性に関するデータを利用しました。
1.2 データの整理
元データからwavefunctionを計算する前に、データの整理を行いました。
元のデータセットからID, smiles, activityのデータ(水溶性に関するデータでは、溶解度をクラス分けしたデータ)を取り出し、csv形式で出力させました。
その際に、こちらのサイトを参考にしてRDKitによりsmilesからMolオブジェクトを生成可能か判定し、生成できない分子は削除しました。
# smilesからrdKitのMolオブジェクトの構築
PandasTools.AddMoleculeColumnToFrame(frame=df, smilesCol = 'smiles')
# 読み込めない分子を削除
df['MOL'] = df.ROMol.map(lambda x: False if x == None else True)
del_index = df[df.MOL == False].index
edited_df = df.drop(del_index)
詳しくはソース(Ames, Solubility)を見てください。
wavefunctionの計算
今回wavefunctionの計算はPsi4を用いて行いました。
まず、上記のように整理したデータのcsvファイルから、IDとsmilesを読み込みました。
そして、読み込んだsmilesからMolオブジェクトを生成し、三次元構造への起こし上げ、水素の付加を経て、wavefunctionを計算するためのインプットデータを作成しました。(こちらのサイトを参考にしました。)
# smilesから三次元構造を作る→雑に構造最適化
mol = Chem.MolFromSmiles(smile) #Molオブジェクトの生成
mol = Chem.AddHs(mol) #水素付加
params = ETKDGv3()
params.randomseed = 1
EmbedMolecule(mol, params) #三次元に拡張
# MMFF(Merck Molecular Force Fieldで構造最適化
MMFFOptimizeMolecule(mol)
conf = mol.GetConformer()
# プラスとマイナスの数を数える
plus = smile.count('+')
minus = smile.count('-')
# 電荷の計算
charge = plus - minus + 0
# Psi4に入力可能な形式に変換
#電荷とスピン多重度の設定
mol_input = str(charge) + " 1"
print(str(i+1) + ": " + mol_input + ": "+ smile)
# 各々の原子の座標をXYZで記述
for atom in mol.GetAtoms():
mol_input += "\n" + atom.GetSymbol() + " " + str(conf.GetAtomPosition(atom.GetIdx()).x)\
+ " " + str(conf.GetAtomPosition(atom.GetIdx()).y)\
+ " " + str(conf.GetAtomPosition(atom.GetIdx()).z)
molecule = psi4.geometry(mol_input)
こうして、作成したインプットデータをこちらのサイトを参考にしてタイムアウトを設定した関数に渡して、wavefunctionを計算しました。
@timeout(timeout_sec)
def opt(level, molecule):
energy, wave_function = psi4.optimize(level, molecule=molecule, return_wfn=True)
return energy, wave_function
計算手法及び既定関数はHF/STO-3Gを用いました。
level = "HF/sto-3g"
こうして計算されたwavefunctionは後の計算で用いやすいようにファイル名にIDを加えて.npyファイルとして出力しました。
# wavefunctionの書き出し
wave_function.to_file("../WaveFunctions/Ames/{}_Ames_wavefunction".format(ID))
詳しくはソース(Ames, Solubility)を見てください。
2.wavefunctionからSDFファイルへ
次に、計算されたwavefunctionやsmilesデータから様々な分子情報を取り出し、それらを分子プロパティ及び原子プロパティとして分子に組み込みSDFファイルにまとめ学習に必要なデータとして出力しました。
2.1 量子計算結果の取り出し
分子情報はRDKit及びPsi4により取り出しました。
分子に関しては体積、エネルギー、HOMO・LUMO準位、HOMO・LUMOギャップ、MULLIKEN電荷・Löwdin電荷の平均と分散、双極子モーメント、原子数、分子量、密度の13プロパティ、
原子に関してはMULLIKEN電荷、Löwdin電荷、原子の質量、原子の座標、原子記号の5プロパティを出力させました。
※以降これらの計算結果をまとめて量子計算結果と言います。
RDKitを使って、smilesから三次元へたたき起こしたMolオブジェクトから体積を計算し、取り出しました。
"""rdkit"""
rdmol = Chem.AddHs(Chem.MolFromSmiles(smile)) #rdkitのmolオブジェクトの生成
AllChem.EmbedMolecule(rdmol)
vol = AllChem.ComputeMolVolume(rdmol) #体積の計算
mol_features.append(vol)
mol_features_name.append('Volume')
体積、密度以外のデータはPsi4を用いてwavefunctionから計算しました。
"""psi4"""
#energy
energy = wf.energy() #total energyの獲得
mol_features.append(energy)
mol_features_name.append('Energy')
#homo/lumo
LUMO_idx = wf.nalpha()
HOMO_idx = LUMO_idx - 1
homo =wf.epsilon_a_subset("AO", "ALL").np[HOMO_idx] #HOMO準位の獲得
lumo = wf.epsilon_a_subset("AO", "ALL").np[LUMO_idx] #LUMO準位の獲得
mol_features.append(homo)
mol_features_name.append('HOMO')
mol_features.append(lumo)
mol_features_name.append('LUMO')
HLgap = lumo - homo
mol_features.append(HLgap)
mol_features_name.append('HLgap')
#MULLIKEN電荷
psi4.oeprop(wf, "MULLIKEN_CHARGES")
Mcharges = np.array(wf.atomic_point_charges())
mol_features.append(np.average(Mcharges))
mol_features_name.append('Mcharge_ave')
mol_features.append(np.var(Mcharges))
mol_features_name.append('Mcharge_var')
atom_features.append(Mcharges.tolist())
atom_features_name.append('Mcharges')
#Löwdin電荷
psi4.oeprop(wf, "LOWDIN_CHARGES")
Lcharges = np.array(wf.atomic_point_charges())
mol_features.append(np.average(Lcharges))
mol_features_name.append('Lcharge_ave')
mol_features.append(np.var(Lcharges))
mol_features_name.append('Lcharge_var')
atom_features.append(Lcharges.tolist())
atom_features_name.append('Lcharges')
#dipole
dipole_x, dipole_y, dipole_z = wf.variable('SCF DIPOLE X'), wf.variable('SCF DIPOLE Y'), wf.variable('SCF DIPOLE Z')
dipole_moment = np.sqrt(dipole_x ** 2 + dipole_y ** 2 + dipole_z ** 2)
mol_features.append(dipole_moment)
mol_features_name.append('dipole')
#atomごとの取り扱い
mol = wf.molecule() #molオブジェクトの生成
atom_num = mol.natom() #atom数
mol_features.append(atom_num)
mol_features_name.append('Atom_num')
#mass
atom_mass_list = []
x_dem_list = []
y_dem_list = []
z_dem_list = []
symbol_list = []
for n in range(atom_num):
mass = mol.mass(n)
atom_mass_list.append(mass)
xyz = mol.xyz(n) #XYZ座標の獲得
x_dem_list.append(xyz[0]) #X座標の獲得
y_dem_list.append(xyz[1]) #Y座標の獲得
z_dem_list.append(xyz[2]) #Z座標の獲得
symbol_list.append(mol.symbol(n)) #元素記号の獲得
atom_features.append(atom_mass_list)
atom_features_name.append('Mass')
mol_mass = sum(atom_mass_list)
mol_features.append(mol_mass)
mol_features_name.append('Mass')
atom_features.append(x_dem_list)
atom_features_name.append('X_dem')
atom_features.append(y_dem_list)
atom_features_name.append('Y_dem')
atom_features.append(z_dem_list)
atom_features_name.append('Z_dem')
atom_features.append(symbol_list)
atom_features_name.append('Symbol')
最後に、体積と分子量の結果から密度を計算しました。
#density
dens = mol_mass/vol
mol_features.append(dens)
mol_features_name.append('Density')
2.2 SDF化
こうして得られた計算結果をこちらを参考にし、SDFファイルへとまとめました。
SDF化する際に必要となるそれぞれの分子の原子座標はPsi4により構造最適化された座標を用いようとしたのですが、Molオブジェクトの形式が異なるため、RDKitにりSDFに組み込むことができず、今回はRDKitによりsmilesから三次元へたたき起こしたMolオブジェクトの座標を用いました。
また、学習に必要な答えとなるデータ(Ames試験データではActivity、水溶性に関するデータでは溶解度をクラス分けしたデータ)も組み込みました。
詳しいコードはソース(Ames, Solubility)を見てください。
3.機械学習モデルの構築
今回は上記のようにして用意した量子計算結果とRDKitによって計算されるFingerprintを用いて決定木、ランダムフォレスト(RF)、グラフニューラルネットワーク(GNN)の3つの手法により、学習を行いました。
決定木とRFでは分子プロパティデータのみを用い、GNNではそれに加え原子ごとのプロパティデータも用いました。
3.1 決定木
まずは量子計算結果などが入っているSDFファイルを読み込みました。
# SDFファイルの読み込み
mol_list = Chem.SDMolSupplier("../../ForMolPredict/SDF_files/Ames/Ames_AllMol.sdf",removeHs=False)
mol_num = len(mol_list)
print("there are {} molecules".format(mol_num))
その後、量子計算後のデータの取り出しとFingerprintの計算を行い、それぞれ、Fingerprintのみのデータセット、量子計算結果のみのデータセット、それらを合わせたデータセットに分けました。
Fingerprintについては166個に分類された部分構造その分子がもっているかを0(もっていない)と1(もっている)であらわすMACCS keysを用いました。
# データの抽出
act_list = [mol.GetDoubleProp('Activity') for mol in mol_list]
mol_props = ['Volume', 'Energy', 'HOMO', 'LUMO', 'HLgap', 'Mcharge_ave', 'Mcharge_var', 'Lcharge_ave', 'Lcharge_var', 'dipole', 'Atom_num', 'Mass', 'Density']
maccskeys = []
calc_list = []
for mol in mol_list:
maccskey = [float(x) for x in AllChem.GetMACCSKeysFingerprint(mol)]
maccskeys.append(maccskey)
mol_data = [mol.GetDoubleProp(prop) for prop in mol_props]
calc_list.append(mol_data)
maccs_df = pd.DataFrame(maccskeys)
Calc_df = pd.DataFrame(calc_list, columns=mol_props)
FC_df = pd.concat([Calc_df, maccs_df], axis=1 )
また、量子計算結果は様々な値をもっているためそれらを0-1の範囲に規格化しなおしたデータも用意しました。(規格化した量子計算結果)
# データの規格化
def rescaling(features):
norm_features = []
max_value = max(features)
min_value = min(features)
for feature in features:
norm_feature = (feature - min_value)/(max_value - min_value)
norm_features.append(norm_feature)
return norm_features
resc_list = []
for prop_name, prop_data in Calc_df.iteritems():
resc_list.append(rescaling(prop_data))
rescCalc_df = pd.DataFrame(resc_list, index=mol_props)
rescCalc_df = rescCalc_df.T
rescFC_df = pd.concat([rescCalc_df, maccs_df], axis=1 )
こうして用意した各分子ごとのデータの数はこのようになりました。
print('number of Fingerprint:',len(maccs_df.columns))
print('number of Calclation Data:', len(Calc_df.columns))
print('number of All Data:', len(FC_df.columns))
print('number of Rescaled Calclation Data:', len(rescCalc_df.columns))
print('number of Rescaled All Data:', len(rescFC_df.columns))
Ames試験データでは
number of Fingerprint: 167
number of Calclation Data: 13
number of All Data: 180
number of Rescaled Calclation Data: 13
number of Rescaled All Data: 180
水溶性に関するデータは
number of Fingerprint: 167
number of Calclation Data: 13
number of All Data: 180
number of Rescaled Calclation Data: 13
number of Rescaled All Data: 180
また、それぞれの答え(0か1)を持つ分子の数はそれぞれこのようになりました。
print('number of 0.0: ',act_list.count(0.0))
print('number of 1.0: ',act_list.count(1.0))
Ames試験データでは
number of 0.0: 2808
number of 1.0: 3326
水溶性に関するデータでは((A) lowを0それ(B) medium,(C) highを1とした)
number of 0.0: 484
number of 1.0: 730
その後これらのデータを学習用データとテスト用データに分け、scikit-learnのDecisionTreeClassifierを用いて決定木に組み込み学習させました。
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(maccs_df, act_list, random_state= 0)
tree = DecisionTreeClassifier(random_state= 0)
tree.fit(x_train, y_train)
詳しくはソース(Ames, Solubility)を見てください。
3.2 ランダムフォレスト(RF)
RFでは決定木と同様にSDFファイルからの量子計算結果を取りだし、Fingerprintの計算、量子計算結果の規格化を行い、学習用のデータセットを作りました。
その後、これらのデータセットをscikit-learnのRandomForestClassifierを用いてランダムフォレストを実装し、学習させました。
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(FP_df, act_list, random_state=0)#test_size=0.25(default)
forest = RandomForestClassifier(max_depth=100, n_estimators=500, random_state=0)
forest.fit(X_train, y_train)
詳しくはソース(Ames, Solubility)を見てください。
4.物性予測モデルの評価
決定木及びRFで学習した結果をFingerprintのみの場合、量子計算結果のみの場合(規格化前と規格化後それぞれ)、それらを組み合わせた場合に分け、混同行列により評価しました。
4.1 評価方法
テストデータの評価値(y_pred)を計算し、
y_pred = tree.predict(x_test) #決定木
y_pred = forest.predict(X_test) #RF
下の関数を使って混同行列、正解率、適合率、再現率を計算表示させ評価しました。
def evaluation(y_test, y_pred):
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score
import seaborn as sns
matrix_fp = confusion_matrix(y_test, y_pred)
sns.heatmap(matrix_fp, square=True, annot=True, cbar=False, fmt='d', cmap='GnBu')
print('Accuracy(正解率): {:.3f}'.format(accuracy_score(y_test, y_pred)))
print('Precision(適合率): {:.3f}'.format(precision_score(y_test, y_pred)))
print('Recall(再現率): {:.3f}'.format(recall_score(y_test, y_pred)))
特徴量に対してはその重要度(importance)を計算し、上位20項目を見ることで評価しました。
# Feature Importance
fti = tree.feature_importances_
fti_df = pd.DataFrame(fti, columns = ['importance'])
# sort
fti_df = fti_df.sort_values("importance", ascending=False)
また、決定木に関しては木の深さ(max_depth)を、RFについては決定木の数(n_estimators)を変化させ、正解率に対してプロットし、その変化を評価しました。
## 決定木の深さ
accs_train = []
accs_test = []
deep = 40
depth = range(1,deep)
for i in depth:
tree2 = DecisionTreeClassifier(max_depth=i, random_state=0)
tree2.fit(x_train, y_train)
acc_train = tree2.score(x_train, y_train)
acc_test = tree2.score(x_test, y_test)
accs_train.append(acc_train)
accs_test.append(acc_test)
# 木の数
tree_num = range(1,500)
training_acc1 = []
test_acc1 =[]
for N in tree_num:
nforest1 = RandomForestClassifier(max_depth=100, n_estimators=N, random_state=0)
nforest1.fit(X_train, y_train)
training_acc1.append(nforest1.score(X_train, y_train))
test_acc1.append(nforest1.score(X_test, y_test))
4.2 評価1(決定木)
決定木を用いた際の学習の結果は以下のようになりました。
混同行列による評価
Ames試験データでは量子計算結果のみの場合ではFingerprintのみの結果に劣るものの、二つのデータを合わせると学習の効率が若干上がりました。
Ames試験データ

一方、水溶性に関するデータでは量子計算結果のみの結果だけでもFingerprintのみの結果よりも良い結果を示し、二つのデータを組み合わせることで更なる向上が見られました。
水溶性に関するデータ

特徴量に関する評価と決定木
学習に用いた特徴量をその重要度順に示し、決定木の一部をここに示します。
重要度のグラフでは、Aems試験データと水溶性に関するデータのどちらでも量子計算結果の重要度が高くなっていることが分かります。また決定木からも量子計算結果によりしっかりと分類がされていることが分かります。
Ames試験データ

決定木の詳細に関してはソース(Ames, Solubility)をご覧ください。
決定木の深さに関する評価
Ames試験データでも水溶性に関するデータでも量子計算結果を加えことにより、やや学習の効率が上がっていることが分かりました。

4.3 評価2(ランダムフォレスト)
RFによる学習の結果は以下のようになりました。
混同行列による評価
決定木における結果と同じくAmes試験データでは量子計算結果のみの場合よりFingerprintのみの方が良い学習を示しましたが、この二つを組み合わせることにより学習の向上が見られました。
Ames試験データ

水溶性に関するデータでも決定木の結果と同様に量子計算結果のみでもFingerprintのみの結果よりも良い学習をし、二つを組み合わせることで更なる学習の向上を見ることができました。
水溶性に関するデータ

特徴量に関する評価
特徴量に関する評価は重要度の値は小さくなっているものの、決定木の時と同様に量子計算結果の重要度が上がっていることが見て取れます。(Fingerprintの結果はその番号により示されています。)
Ames試験データ
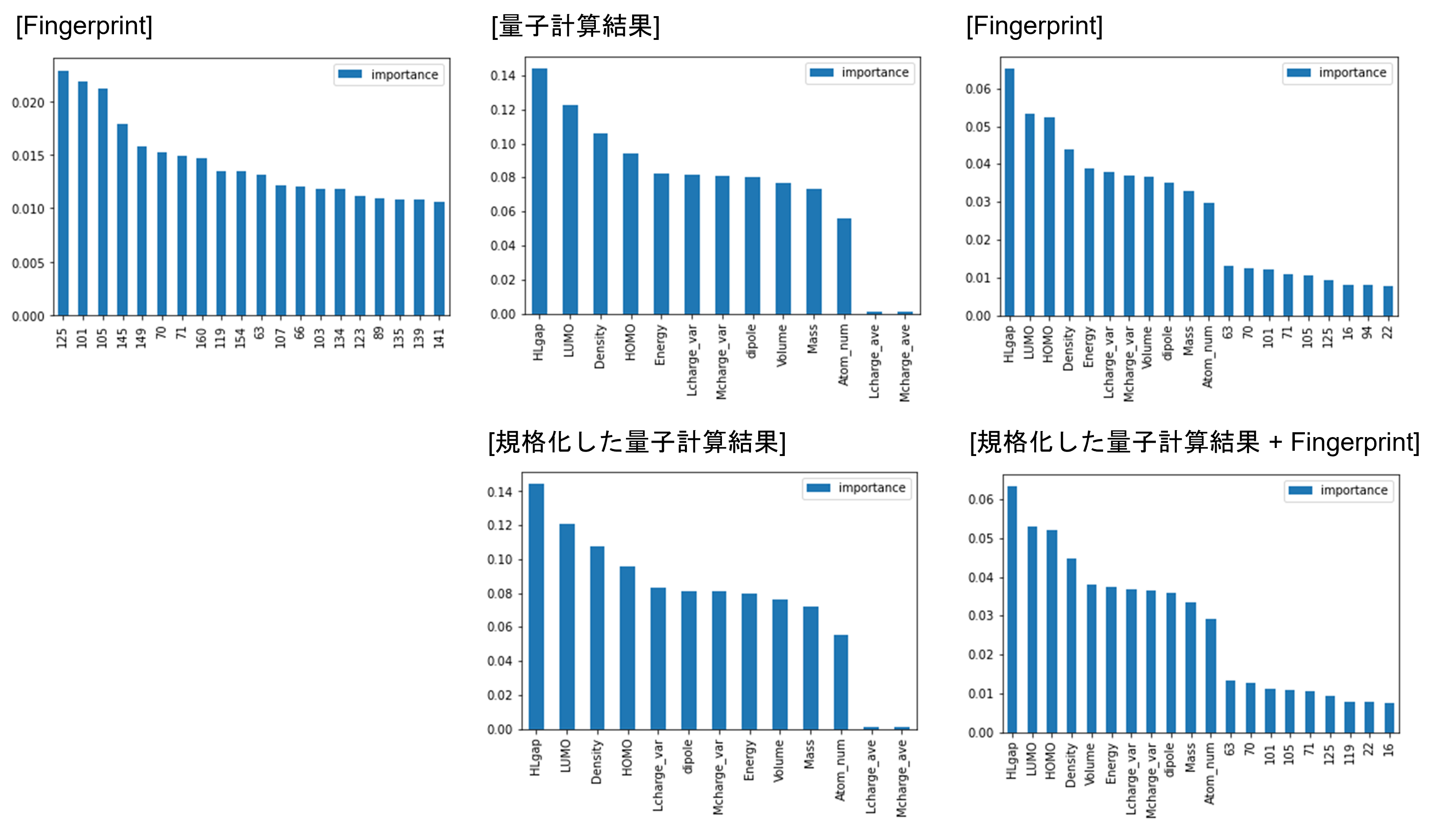
木の数に対する評価
Ames試験データでは量子計算結果のみの場合ではtestの正解率はFingerprintのみの場合と比べると低い値を示していますが、trainの正解率は上がっていることが分かります。
また、これら二つを組み合わせることで、testの正解率が若干向上し、trainの正解率も向上することがわかりました。
水溶性に関するデータでは量子計算結果を加えることでtest、trainともに正解率が向上し、計算データのみの結果でも正解率が向上していました。

5.グラフニューラルネットワーク(GNN)での実装
今回作成したSDFファイルから分子情報や量子計算結果を取り出し、pytorchを使ったGNNでも予測モデルの学習データに加えることで物性の予測性能が上がるかどうかを検証してみました。
5.1 量子計算結果の組み込み
GNNでは分子に関するデータだけではなく、原子に関するデータも組み込みました。
(量子計算結果の詳細についてはこのページの2.1節を参照してください。)
※原子ごとにデータを作っているため、分子に関するデータはその分子に含まれるすべての原子が同じ値を持っているものとして扱いました。
def get_WF_results(mol):
mol_props = ['Volume', 'Energy', 'HOMO', 'LUMO', 'HLgap', 'Mcharge_ave', 'Mcharge_var', 'Lcharge_ave', 'Lcharge_var', 'dipole', 'Atom_num', 'Mass', 'Density']
atom_props = ['Mcharges', 'Lcharges', 'Mass', 'X_dem', 'Y_dem', 'Z_dem']
mol_datalist = []
WF_results = []
for mol_prop in mol_props:
mol_datalist.append(mol.GetDoubleProp(mol_prop))
for atom in mol.GetAtoms():
atom_data = []
for atom_prop in atom_props:
atom_data.append(atom.GetDoubleProp(atom_prop))
molatom_data = mol_datalist + atom_data
WF_results.append(molatom_data)
return np.array(WF_results, dtype=np.float32)
詳しくはソース(Ames, Solubility)を見てください。
5.2 結果
Epochを100まで学習させた結果を示します。
Ames試験データではwavefunction(WF)から計算したデータ(量子計算結果)を加えてないものではEpoch40あたりからValidation lossが増え始め、過学習となっていました。
test lossは過去に計算されたベストのモデルを用いて計算されているため、過学習になり始めてからは一定の値を示しました。量子計算結果を加えたものはvalidation lossも少しずつ下がっており過学習にはなっていませんが、結果としては計算データを加えてないものの方が良いモデルを作れていたという結果になりました。
水溶性に関するデータでも量子計算結果を加えて加えてないものの結果はEpoch60あたりから過学習になってしまっており、量子計算結果を加えたものはその後も過学習にはなりませんでした。Ames試験データの結果では量子計算結果を加えない方が良いモデルを作れるという結果になりましたが、水溶性に関するデータでは量子計算結果を加えた方がTest lossが小さくなっておりより良いモデルを作ることができました。

※凡例の後ろに(WF)を付けているものが量子計算結果を加えた結果になります。
6.まとめ・感想
今回は量子化学計算ソフトウェアであるPsi4を用いてwavefunctionを計算し、そこから軌道準位や電荷分布などのより高度なパラメータ(量子計算結果)を分子の物性予測モデルに組み込むことで、そのモデルの機能が向上するか検討してみました。
決定木やRFの結果では量子計算結果を加えることにより予測の向上が見られました。
特徴量の評価ではAmes試験データではHOMO・LUMOギャップの値が高い重要度を示す一方、水溶性に関するデータでは体積、質量、電荷の分散の値が高い重要度を示しており、これは直感的にも水溶性に関係ありそうなパラメータなので、その特徴量の重要度が高くなっているのはとても興味深いと思いました。(Ames試験データの結果については遺伝子の突然変異を引き起こすにはどのパラメータが効いてきそうか直感的にわからないので、言及は避けておきます。)
GNNの結果では量子計算結果を加えても思ったよりモデルの精度は上がらず、機械学習の難しさを体験しました。
(この記事は研究室インターンで取り組みました:https://kojima-r.github.io/kojima/)

