この記事は東大航空宇宙2023 Advent Calendar 2022の16日目の記事です。2023年4月進学予定者の現B2の学生が面白い記事を書いてますので、他の記事も是非読んでみてください。
我々航空宇宙工学科の2年生は、未だあまり専門的な話はやらずに基礎を固める座学の授業を受けることが多いです。
さて、ある日熱力学の授業にて、ファンデルワールス方程式に従う気体の断熱変化に伴って、
\left(p+\frac{a}{v^2}\right)(v-b)^{\frac{R}{C_v}+1} = \mathrm{const.}
となる、という話がありました。私はその導出・数式を見て、特に疑問を抱くこともなくそうなのかあと思っていました。ところが、その日の帰り道、9日目の記事を書いてくれたyasyas0124さんに教員の説明が誤っているのではないかと教えてもらいました。$C_v$は$T$の関数であるからこれではいけないのではないか、というのです。確かに導出をもう一度眺めてみると、$C_v$が$T$の関数であると考えるとその導出がうまくいかない部分が存在していました。そこでこの問題について調べてみることにしました。以下、様々な小文字の示量変数は工学っぽくkgベースとします。したがって気体定数$R$もkgベースです。それからこの記事は全くプログラムメインではないです。しかしグラフ化の際にpythonを使っているので、それで許していただけると幸いです。また、この内容が正しい保証はありません。ご容赦願います。
問題の整理
とりあえず私の復習も兼ねて、問題を整理しておきたいと思います。
理想気体では、分子間力、分子の大きさを無視し、状態方程式は
pv = RT
となります。一方実在気体では分子間力、分子の大きさを無視できません。そこで、ファンデルワールス方程式では、実在気体の状態方程式を以下のようにして近似します。
(p+\frac{a}{v^2})(v-b) = RT
ここで$a, b$はその気体ごとに定まる定数です。それぞれ分子間力、分子の大きさを補正する目的で付け加えられています。
さて、この方程式に従う気体が断熱変化を起こすとき、授業では以下のように定数が見出されました。まずは一般的に$du$がどう書けるかを求めておきます。熱力学第一法則より
du = \delta q_{in} - pdv
となります。これを変形していきます。
\begin{align}
du &= \delta q_{in} - pdv\\
&= T ds - pdv\\
&= T \left\{ \left( \frac{\partial s}{\partial T} \right)_v dT + \left( \frac{\partial s}{\partial v} \right)_T dv \right\} - pdv\\
\end{align}
ここで$dT$の項に注目すると、ここは$T\delta s$が$v$一定とした時の$\delta q_{in}$にあたることから、定積比熱$C_v$にあたります。さらにMaxwellの関係式より$\left( \frac{\partial s}{\partial v} \right)_T = \left( \frac{\partial p}{\partial T} \right)_v$です。したがって
\begin{align}
du &= C_v dT + \left\{ T \left( \frac{\partial p}{\partial T} \right)_v - p \right\}dv
\end{align}
となります。ここでファンデルワールス方程式に従う気体の断熱変化の話に戻ります。ここで求めた$du$の式を用いて、断熱ですから、熱力学第一法則から
\begin{align}
0 &= \delta q_{in} \\
&= du + pdv\\
&= C_v dT + T\left( \frac{\partial p}{\partial T} \right)_v dv
\end{align}
となります。今回扱っている気体はファンデルワールス状態方程式に従いますので、$T\left( \frac{\partial p}{\partial T} \right)_v = \frac{RT}{v-b}$となります。これを代入して適当に割り算すると、
C_v \frac{dT}{T} + R \frac{dv}{v-b} = 0
となります。これを両辺積分して
C_v \ln \frac{T}{T_0} + R \ln \frac{v-b}{v_0-b} = \mathrm{const.}
となります。これをもう少し変形すると
\left(p+\frac{a}{v^2}\right)(v-b)^{\frac{R}{C_v}+1} = \mathrm{const.}
となります......というのが授業内容でした。ところがもし$C_v$が$T$の関数であれば、このひとつ前の積分のところがおかしいです。この積分は$C_v$が定数でないと成立しません。
Cvが変数とするとどうなるか
まず$C_v$が本当に変数なのかどうか、インターネット上で検索をかけてみたら、以下の表が引っかかりました。
https://takun-physics.net/wp-content/uploads/2019/10/1-2.png
実際に$T$に依存するようです。以下、この表をもとに計算していきます。ここで$C_v$を2次で以下のように近似することを考えます。
C_v(T) = C + AT + BT^2
このとき、上の導出における積分のところは
\left(C+AT+BT^2\right) \frac{dT}{T} + R \frac{dv}{v-b} = 0\\
\therefore C \frac{dT}{T} + R\frac{dv}{v-b} = -(A+BT)dT\\
\therefore C \ln \frac{T}{T_0} + R \ln \frac{v-b}{v_0-b} = -AT - \frac{1}{2} B T^2
となります。もう少し変形すると、Dたちを適当な定数として
T (v-b)^{\frac{R}{C}} = D_1 e^{-\frac{A}{C}T-\frac{B}{2C} T^2}\\
\therefore \left(p+\frac{a}{v^2}\right)(v-b)^{\frac{R}{C}+1} = D_2 e^{-\frac{A}{C}T-\frac{B}{2C} T^2}
となります。
差を可視化する
さて、冒頭での式とここで求められた式はどの程度異なるのでしょうか。ここでpythonを用いて数値計算の卵を行います。ここでは、とりあえずの例として空気を対象に扱うことにします。まず空気の$C_v$の表をkgベースに書き換え、scipyのoptimizeライブラリを用いてフィッティングを行います。結果がこちらです。

数値は以下のようになりました。
A =0.0002205469158670386\\ B = -4.061725152853897 \times 10^{-8}\\ C = 0.7077386304572676
次に、これを用いてpV線図を描いていきます。ここが案外大変でした。私の書いた汚いプログラムをお見せするのは憚られるので方針だけ書いておきます。ファンデルワールス方程式のa, b, cはwikipediaの値を用いました。それから特徴的なp, v, Tの値としてこれもwikipedia記載の臨界定数を用いました。この臨界状態から断熱に変化した時の線を描くことを目的に据えます。ここで、$T$を指定したときに$v$や$p$を求める関数を、$C_v$が一定である場合、$C_v$が$T$による場合、それぞれの式に対して作り、そこから求められた$p, V$をグラフ化しました。さて、このようにして作ったプログラムにより計算された結果によると、$T$=100〜200Kで変化させたときのグラフは以下のようになりました。青いグラフが冒頭に紹介した$C_v$が一定であると考えているであろう式によるもの、オレンジのグラフが今回作成した式によるものです。

あまり変化がないように見えます。と、ここまでをyasyas0124さんに報告したところ、温度の範囲を大きくした方が良いのではないかというアドバイスをいただき、$T$=100〜2000で変化させたときのグラフを描いてみると......
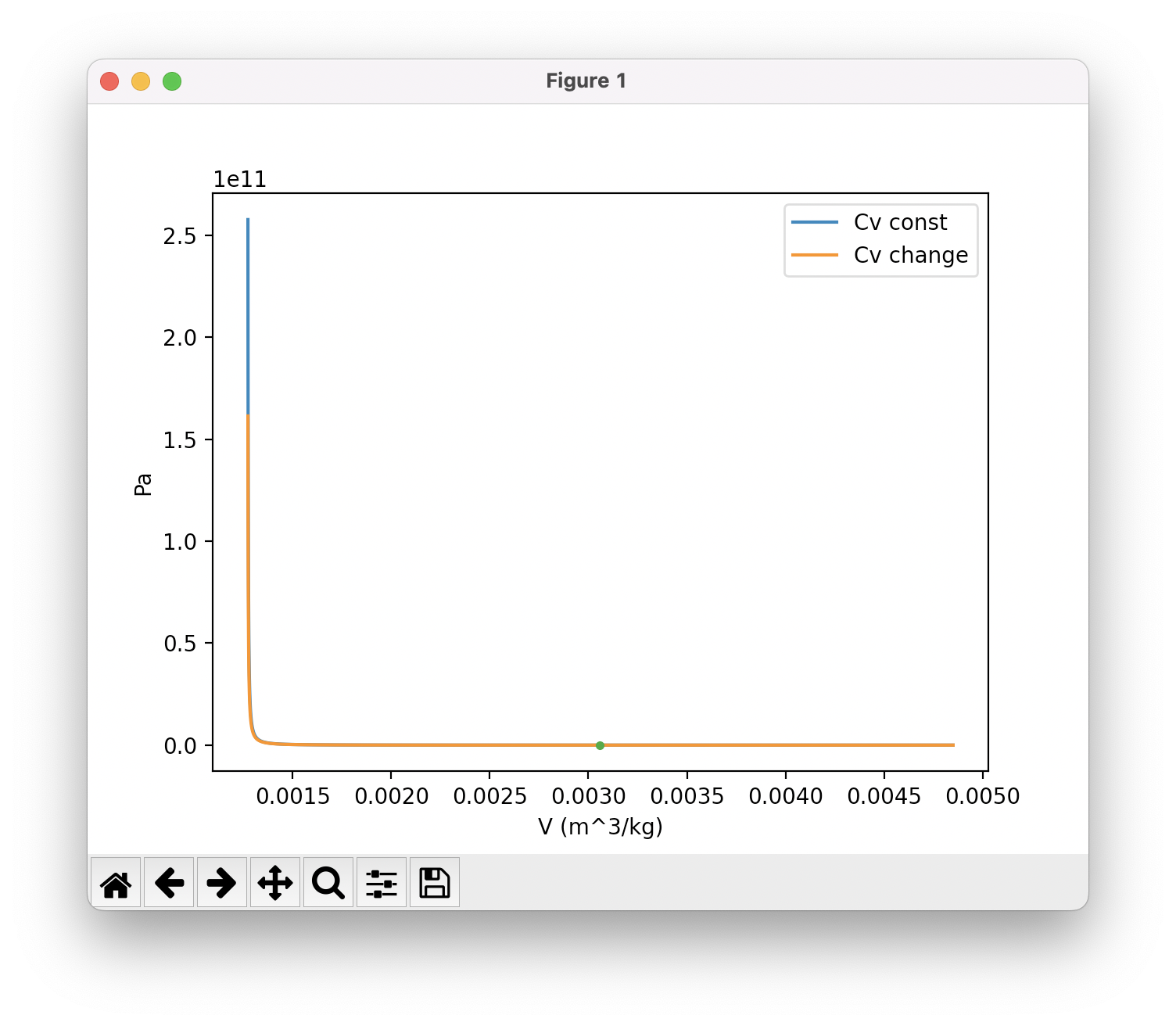
とこのように、何か差が出ていそうです。このままではよくわからないので$T$=1500〜2000のところだけプロットしてみると、以下のようになりました。

どうやらここまで温度を大きく変化させると$p$で見て1.5倍くらいの差は出ているようです。一方$v$で見るとあまり違いがなさそうです。
結論
もし今回導いた式が正しいとすると、温度が100Kくらいしか変わらない状況ではあまり変化が見られないものの、数1000Kも変わる状況では圧力に関してある程度の差が見られるようです。このような状況があり得るのかというと、まさにロケットエンジンの中では燃料は数10Kであるのに燃焼室では数1000Kにするようであるので、そのような状況を扱うときには注意するべきかもしれません。しかし実際のところファンデルワールス方程式は精度が出ないため、あまり実際の技術計算には使われていないらしいです。また、この方法の改善案として、$C_v$の温度による変化の理論を学び(統計力学関連っぽい雰囲気がします)近似せずにきちんと積分することが考えられます。今回はあまり時間がなかったので、そこまでは行いませんでした。