はじめに
みなさんは*"フィッシャーの正確確率検定"と"カイ2乗検定"*という言葉を聞いて, どちらの方がより正確そうだと思いますか?
答えは, 「2者は比較できない」です。
しかし, 生物統計ではこの2者のどちらかを使うかがしばしば問題になり, 「カイ2乗検定が役に立たないシチュエーションでは, フィッシャーの正確確率検定をつかう」と教えられます1。何故でしょうか。
今回は, 両検定の概要(数理的にふみこんだ話はしませんが)とモンテカルロシミュレーションの MATLAB コード, シュミレーションの結果を共有できればと思います。
フィッシャーの正確確率検定とは
フィッシャーの正確確率検定2 (Fisher's exact test) は一つの基準間の独立性の検定の方法です。
基準間の独立性の検定とは, 例えば, 2 つの基準
- エビフライは尻尾まで食べる(基準A)
- 鮭は皮まで食べる(基準B)
を考えた時に, 「エビフライの尻尾を食べる人, 鮭も皮まで食べる説」を検討するために用いられる手法です。もし基準 A と基準 B が独立と言えれば, 「エビフライの尻尾を食べることと, 鮭の皮を食べることは関係ない」と言えるわけです。
話が独立性の検定中心になってしまいました。
フィッシャーの正確確率検定は上記のような例で, 超幾何分布を前提3とした p 値を与えます。
例えば, 下表のように集計されたとします。
| エビの尻尾食べる | エビの尻尾食べない | 列マージン | |
|---|---|---|---|
| 鮭の皮食べる | $a_{11} = 10$ | $a_{12} = 13$ | $a_{11}+a_{12} = 23$ |
| 鮭の皮食べない | $a_{21} = 15$ | $a_{22} = 7$ | $a_{21}+a_{22} = 22$ |
| 行マージン | $a_{11}+a_{21} = 25$ | $a_{12}+a_{22} = 20$ | $a_{11}+a_{12}+a_{21}+a_{22} = 45$ |
フィッシャーの正確確率検定は上の例の, 行マージンと列マージンを固定した場合の超幾何分布 を前提にした, 二つの基準は独立だという帰無仮説 $H_0$ の検定を行います。この検定の $p$ 値は, 「二つの基準は独立だという帰無仮説 $H_0$ の下で, 今回の集計値より極端な例は $p$ の確率でしか起こらないよ」という意味を持ちます。
「今回の集計値より極端な例」とは超幾何分布の元で確率の少ない例を指します。例えば, 下の場合とか。こんな集計がでたら, 「エビフライの尻尾を食べる人, 鮭も皮まで食べる説」は確かに有力そう。
| エビの尻尾食べる | エビの尻尾食べない | 列マージン | |
|---|---|---|---|
| 鮭の皮食べる | $a_{11} = 23$ | $a_{12} = 0$ | $a_{11}+a_{12} = 23$ |
| 鮭の皮食べない | $a_{21} = 2$ | $a_{22} = 20$ | $a_{21}+a_{22} = 22$ |
| 行マージン | $a_{11}+a_{21} = 25$ | $a_{12}+a_{22} = 20$ | $a_{11}+a_{12}+a_{21}+a_{22} = 45$ |
カイ 2 乗検定とは
カイ 2 乗検定 (Chi-squared test)も, 目的や p 値の含意自体は変わりませんが, 想定するモデルが異なります。これは多項分布の以下の値がサンプルサイズが増えるとカイ二乗分布に従うことをその論拠としています。
$$\sum_{i,j} O_{ij} = \frac{(a_{ij}-\hat{a_{ij}})^2}{\hat{a_{ij}}} \sim \chi^2(\nu)$$
ただし, $\nu$ は自由度で, 独立性の検定の場合は $(列数-1)*(行数-1)$になります。
モンテカルロシュミレーション
以上の議論を踏まえ, 両検定を比較してみます。上に「両者は比較できない」と書いていますが, まぁものは試し。
まずはテキトーな値からやってみる
まず, 集計結果から帰無仮説の統計モデルを設定します。この時, 集計結果がよく各基準の多項分布のパラメタを推測できていると仮定しています。
%% INPUT %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
agg = [1 4 ;4 2]; % aggregated result
n_sample = 1000; % sampling based on null hypothesis
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% MODELING %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[n_row, n_col] = size(agg);
sz_sample = sum(agg,'all');
% model based on null hypothesis
mrgn_r = normalize(sum(agg,1),'norm',1);
mrgn_c = normalize(sum(agg,2),'norm',1);
pd_r = makedist('Multinomial',mrgn_r);
pd_c = makedist('Multinomial',mrgn_c);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
これで帰無仮説 $H_0$ に基づいた多項分布を生成できました。帰無仮説では, 2 つの基準は独立, つまり 2 つの多項分布の掛け合わせが想定するモデルになります。
それでは, ここから n_sample4 のサンプル数だけ帰無仮説の下でサンプリングしていきます。
%% SAMPLING %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% prepare for parfor loop
p_chi2 = zeros(1,n_sample);
p_fisher = zeros(1,n_sample);
df = (n_row-1)*(n_col-1);
parfor i = 1:n_sample
sample_table = zeros(n_row,n_col);
chi2_table = zeros(n_row,n_col);
r = random(pd_r,1,sz_sample);
c = random(pd_c,1,sz_sample);
% aggregate in cross table
for j = 1:sz_sample
sample_table(c(j),r(j)) = sample_table(c(j),r(j)) + 1;
end
sample_mrgn_r = repmat(sum(sample_table,1),[2,1]);
sample_mrgn_c = repmat(sum(sample_table,2),[1,2]);
expected_table = (sample_mrgn_c*sample_mrgn_r)/2/sz_sample;
% calculate chi2
for k = 1:n_row
for l = 1:n_col
if expected_table(k,l) ==0
continue % count chi2 as 0, because 0^2/0 ~ 0
else
chi2_table(k,l) = (sample_table(k,l)-expected_table(k,l))^2/expected_table(k,l);
end
end
end
p_chi2(i) = chi2cdf(sum(chi2_table,'all'),df,"upper");
[~,p_fisher(i)] = fishertest(sample_table);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
上のカイ 2 乗分布の $p$ 値の計算は, 本当は crosstab で簡潔に済ませたかったのですが, コクランのルールに引っかかるような小さいサンプルサイズ (<20) の場合, ある基準のクラスがそもそも発生しない可能性もあるので, 工夫が必要でした。
それぞれの $p$ 値が求まったので, その経験的累積分布関数とその 95%CI を ecdf を用いてプロットしていきます。カイ 2 乗分布は赤で, フィッシャーの正確確率検定は緑で書きます。範囲は, 検定の時に問題になるような, $[0, 0.1]$ の範囲で見ることにします。
%%%%%% PLOT %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% plot empirical cumulative distributions
hold off
[chi2_f, chi2_x, chi2_flo, chi2_fup] = ecdf(p_chi2);
plot(chi2_x,chi2_f,'red');
hold on
plot(chi2_x, chi2_flo,':red');
plot(chi2_x, chi2_fup,':red');
[fisher_f, fisher_x, fisher_flo, fisher_fup] = ecdf(p_fisher);
plot(fisher_x, fisher_f,'green');
plot(fisher_x, fisher_flo,':green');
plot(fisher_x,fisher_fup,':green');
% plot F(x) = x for reference
x = 0:0.001:1;
Fx = 0:0.001:1;
plot(x,Fx,'--k');
title(['Empirilcal CDF ; agg = ',mat2str(agg),' ; number of samples = ',num2str(n_sample)]);
xlim([0 .1]);
ylim([0 .1]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
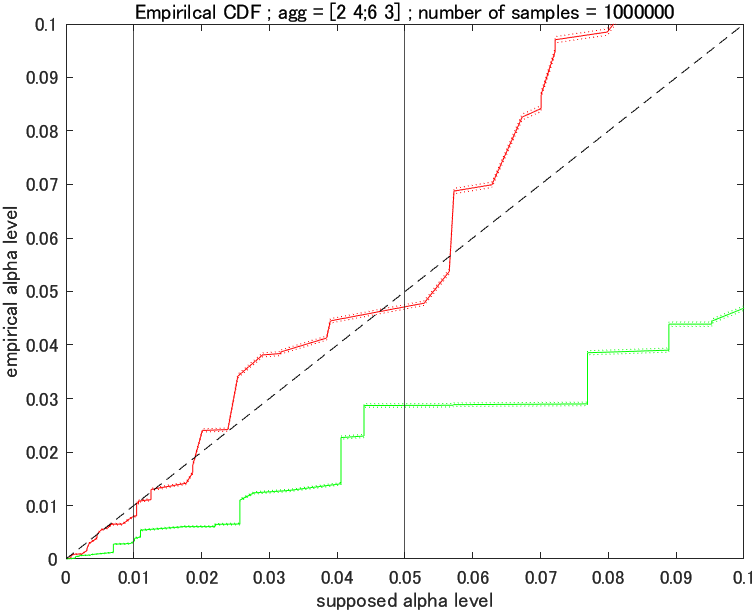
結果は下図のようになりました。図の読み方は, x 軸が検定の時に設定した優位水準, y 軸が経験的に得られた優位水準です。つまり, 「優位水準 $x$ で検定していたつもりだったが, シミュレーションしてみると実際は $y$ の優位水準で検定しているっぽい」という読み方です。
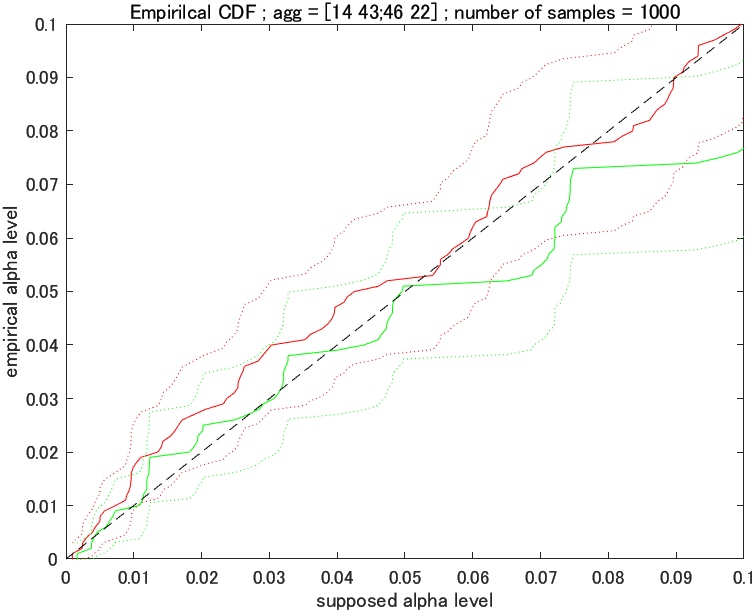
実線の部分だけを見ると, カイ二乗検定の方が優位水準が高く, フィッシャーの正確確率検定の方が優位水準の低い保守的な検定のように見えますが, こんなに信頼区間が大きいと何とも言えなさそう。サンプル数を増やしてみましょう。
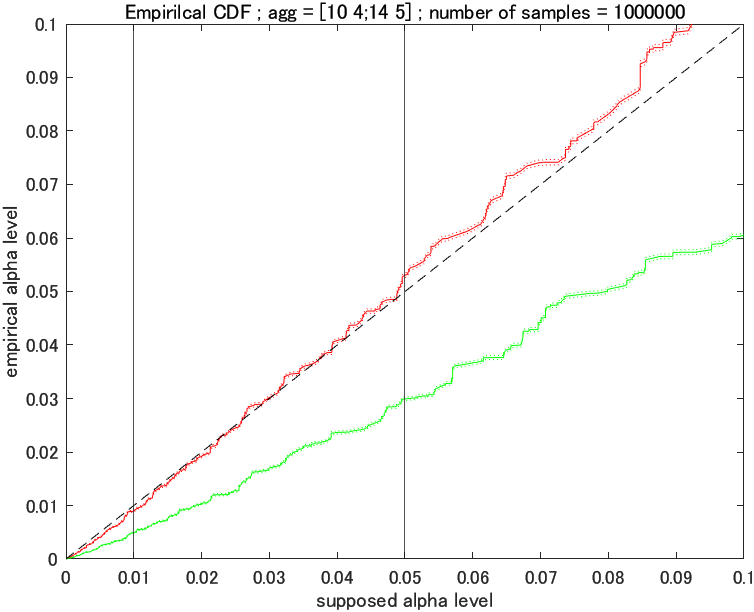
サンプル数を増やしてみる : 1,000,000 5
ついでに, 設定している優位水準が 5%, 1% の時の補助線もたしときました。
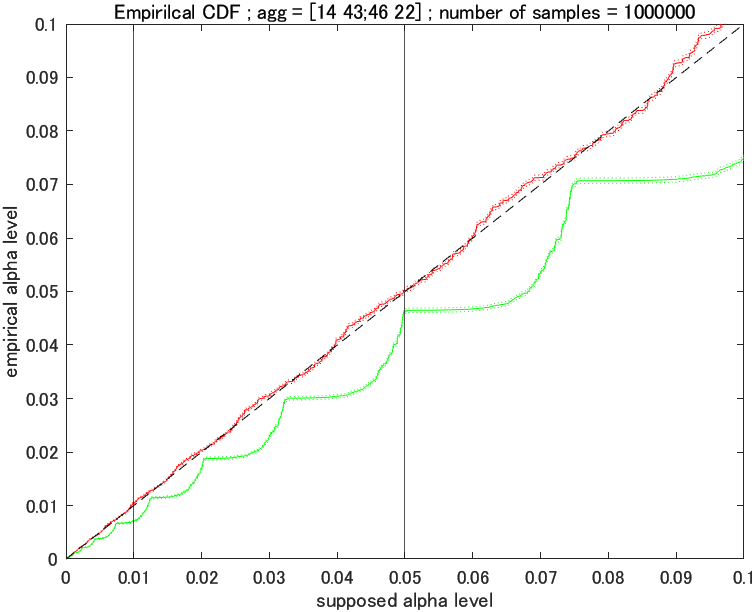
オーバーキル感。調子に乗ってサンプルサイズをとり過ぎたかも (95%CI がもはや見えない)。
集計が $[14, 43; 46, 22]$ のような, サンプルサイズがある程度あるような場合ではカイ二乗検定を使うよう教えられますが, なるほどその通りと言えそうですね。(たまにそのような状況でもフィッシャーの正確確率検定を最善としている生物系の文献を見かけるんですが, それは違うと私は思います。その理由は最後に書きます。)
コクランのルール (Cochran`s Rule) に抵触してみるぜ!
コクランのルールとは, コクラン先生(1958)が「こういう場合以外はカイ二乗検定はあかんで」とする条件のことです。リンク先のページはその背景についてよく説明してくれています。
要約すると, 以下の通りです。
- 自由度が 1 より大きい場合
- 5 未満のセルの数が 1/5 未満6の割合で, 期待度数に 0 がない場合はカイ二乗検定でも OK。(I)
- 2x2 表の場合 (自由度 1)
- サンプルサイズが 20 未満 (II) か,
- サンプルサイズが 20 以上 40 未満かつ最も少ない期待度数が 5 未満の時(III)はフィッシャーの正確確率検定を使う。
- サンプルサイズが 40 以上(IV)の場合は連続補正をしたカイ二乗検定を使え。
コクランのルール (I) に抵触
下の表みたいな場合を考えてシュミレーションしてみます。
| あ | い | う | 列マージン | |
|---|---|---|---|---|
| ア | 12 | 3 | 5 | 20 |
| イ | 4 | 3 | 4 | 11 |
| 行マージン | 16 | 6 | 9 | 31 |
... これはまたやります( MATLAB の fishertest が 2x2 行列までしかサポートしてなかったので)。
コクランのルール (II) に抵触
コクランのルール (III) に抵触
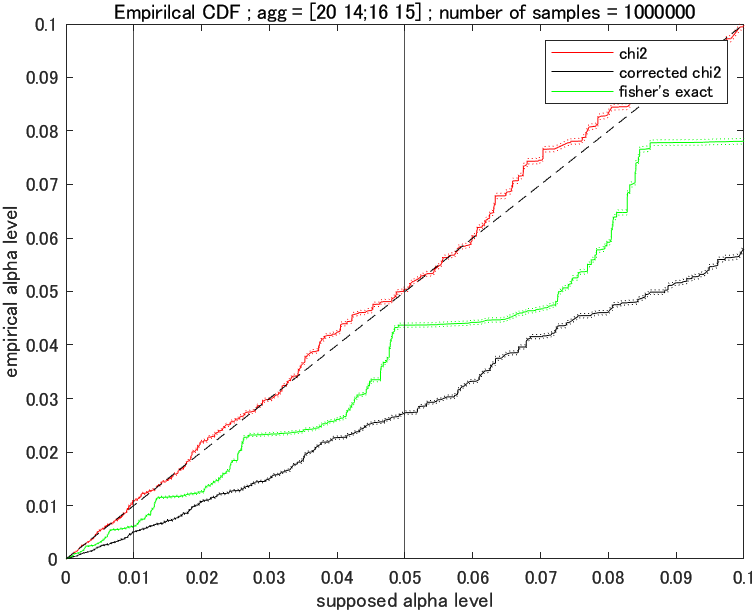
コクランのルール (IV) に抵触
連続補正とは, 下のように離散値である集計値を, 連続型分布であるカイ二乗分布に近づけてみる試みです。(n = サンプルサイズ)
$$\chi_{0}^{2} = \frac {n(|O_{11}O_{22} - O_{12}O_{21}| - n/2)^{2}}
{a_{1\cdot}a_{2\cdot}a_{\cdot1}a_{\cdot2}}$$
コード上では上の値を計算することになります。
chi2 = sz_sample*(det(sample_table)-sz_sample/2)/prod(sample_mrgn_r)*prod(sample_mrgn_c)
流石に 3 本になるので凡例を追加してプロットします。
あれ?フィッシャーの正確確率検定よりもひどいですが?実は, この3 つの関数の関係, とても面白いので $[0,1]$ の範囲まで拡大してみてましょう。
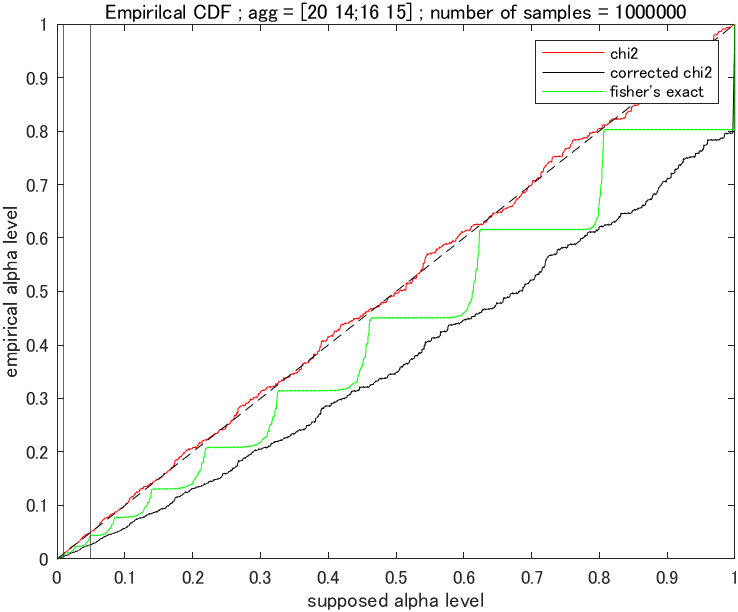
なんと, フィッシャーの正確確率検定が補正ありと補正なしのカイ二乗検定にかわいく収まる形になっています。これを見ると, 「ああ, コクラン先生の『補正ありのカイ二乗を使え』っていうのは, 簡単にシュミレーションできなった時代に『サンプルサイズ 40 以上はフィッシャーの正確確率検定は大変だから, 補正ありのカイ二乗検定でフィッシャーの正確確率検定を近似しちゃっていいよ』ってことを言いたかったんだなぁ」と悟るわけです。
なぜフィッシャーの正確確率検定はしばしば正確でないのか。
答えを言うと, しばしば想定しているモデルが誤っているから。
フィッシャーの正確確率検定は, もともと広く行われる実験を想定したものではありません。
フィッシャーの正確確率検定は, フィッシャー先生が行った Lady tasting tea という実験(勝負?)で用いられたことをその発端とします。この実験は, 「ミルクティーのミルクと紅茶, どっちを先に入れるかで味違くね?」というものを検証するために行われたもので, 被験者は 4 杯のミルク先入れミルクティー, 4 杯の紅茶先入れミルクティー合計 8 つを与えられ, どちらかの味のする 4 杯を当てるというものです。この実験の特徴は, ミルクティーの全数が 8 つと少なく, かつ被検者がそれぞれのミルクティーの数が 4 つと知っている点にあります。表にするの以下のような形です。
| ミルク先入れ | 紅茶先入れ | 列マージン | |
|---|---|---|---|
| 「ミルク先入れ?」 | ? | ? | 4 |
| 「紅茶先入れ?」 | ? | ? | 4 |
| 行マージン | 4 | 4 | 8 |
そう, 上にも書きましたが, フィッシャーの正確確率検定は行マージンと列マージンを固定したモデルを想定しているんですね。
このような実験, そうあるものでしょうか?(反語)
とは言え, 例は考えれば挙げることができます。
とある実験計画で, 「趣味が同じ男女のほうが魅かれあう説」という説を検証しようとした時, 実験計画を, 「男女50人ずつ, 半数はテニスが好き, 半数はサッカー好きであるように人を集め, 一定の自由時間後(全員が)ペアになってもらう」とすると, 以下のような図式が成立します。
| サッカー | テニス | 列マージン | |
|---|---|---|---|
| サッカー | ? | ? | 25 |
| テニス | ? | ? | 25 |
| 行マージン | 25 | 25 | 50 |
このような実験計画をすれば, うまくフィッシャーの正確確率検定の想定するモデルと合致することになります。しかし, 気を付けなければいけないのは 5 % の優位水準は, その再現性を列マージン, 横マージンを全く同じにした場合のものとしているという点です。つまり, 「帰無仮説が正しいとしたら, 100 回とも男女50人ずつ, 半数はテニスが好き, 半数はサッカー好きであるように人を集め実験場合, 今回の実験より極端な結果が起こるのは 5% 以下だよ」と言っているのであって, 集める人数や比率が異なる場合での再現性は保証しないというわけです。
「こんな実験どこにあるんだよ...7」というのが正常な感覚ではないでしょうか。やろうと思えばできますが。
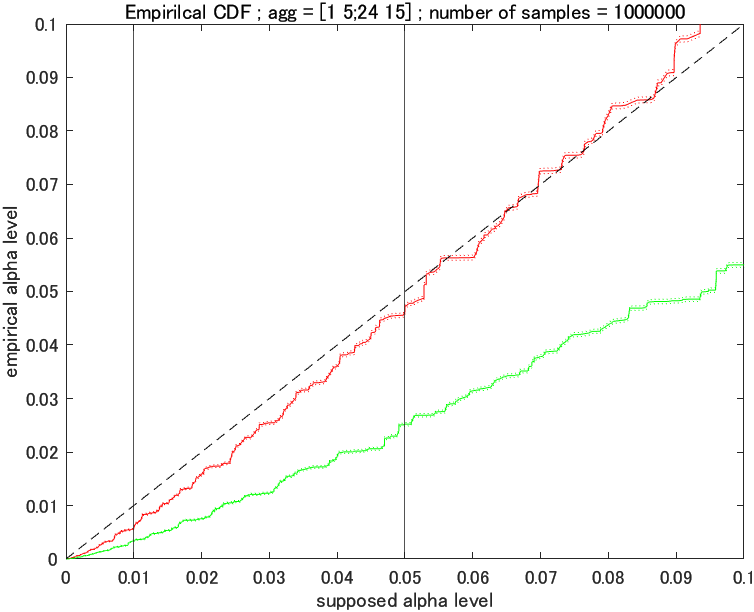
性格が悪いようではありますが, カイ二乗検定よりフィッシャーの正確確率検定を推してそうなページの1例 8での例を取り上げてみても, これはフィッシャーの正確確率検定が想定するモデルではありませんし, 結果も下図の通り,カイ二乗検定のほうがより正確な検定ができているように思われます。「フィッシャーの正確確率検定で優位水準 5% で検定しようと思ってたら, (カイ二乗検定は 4.5% くらいなのに対して, )実は 3 % でやっちゃってました(テヘペロ)」みたいな事態が起こっているわけです。
「フィッシャーの正確確率検定の方が保守的」はもうやめにしませんか?
上のような例を踏まえた上でもフィッシャーの正確確率検定を推奨する方がいますが, これは「フィッシャーの正確確率検定の方が, 下手に帰無仮説を棄却しない, つまり保守的な結果になっている」ことが主な理由です。しかし, これは
- アルファレベル 5% という設定は慣習によるものに過ぎないこと
- たとえ帰無仮説を棄却しても, それは「帰無仮説をモデリングする際のすべての仮定に確率的になんらかの誤りがありそう9」と示唆するだけであること
を考えれば非合理的かと思われます。つまり, 1. に対しては, **「じゃあ最初っから優位水準 3 % とかにしとけばよくね?」という穴, 2. に対しては「別に帰無仮説を棄却したところで, 統計的な検問をクリアしたってだけで, 科学的な一定の性質が肯定されたわけではなくね?」**という穴があるわけです。
上のように各科学の分野で結論に飛びつくことを恐れる姿勢はわかりますが, それは 2. のように統計の威力を過大評価しているだけではないかと思われます。例えば, 生物屋さんはあくまで生物の科学的な機構を発見することが目的であり, 保守的な統計ほどそれを強く証明してくれそうという気持ちはわかりますが, 一方で統計屋さんは優位水準 5% と言われたらなるべくそれに近しいモデルを利用するのが目的となるわけです。
※上の私のような意見は多少過激かもしれません。よく検討してくれている論文 もあるので, そちらも処方しておきます。
じゃあどうすればいいのか
**シミュレーションをすればいいのです。上のような方法を使って。**実験結果を上のようなコードに打ち込んで, 近い分布でシミュレーションし, よりよく近似できているほうを用いればいいのではないでしょうか。
コクランのルールの濫用も, そのルールが当時の技術的な限界からの回避策として提示された背景を鑑みると, 現在やるべきことはシュミレーション技術の民衆化かと思われます。
なので, 上の私が書き散らしたようなコードも気が向いたときに整理して再掲しておきます。MATLAB しか使えないような人がこれを機にシミュレーションを日常化してくれればいいなとか思ったり。(シミュレーションはパソコンの身丈にあった回数を...!)
-
現に, 私も学校の実験でそう教わりました。 ↩
-
日本語版の wiki は誤解を導きそうなので, オススメしません。 ↩
-
ここの前提が誤解を生んだ諸悪の根元だと言え, 逆に言えばめっちゃ重要な部分です。 ↩
-
gpuArray を用いたものも気が向いたら追加しようかと思います。(GeForce RTX 2080 Ti を使ってあげたい) ↩
-
8 ワーカーで 30 秒弱といった程度です。(プロセッサは Inter(R) Core(TM) i9-9900KS CPU @ 4.00GHz 4.00GHz) ↩
-
具体的な数値は指定されていないが, 例示として 1/5 が挙げられている。コクラン先生は感覚でものを語っちゃう人だったのかも。 ↩
-
筆者は大学で「アルコールの分解酵素の遺伝子の遺伝型と, アルコールパッチテストの結果との独立性の検定」の場合に推奨されました。この場合どっちのマージンも固定されてない例になります。 ↩
-
この方自体の医療に関する知見は超一流なので, オススメです。ただ, 該当の記事にだけ?ポイントがあっただけということです。 ↩
-
p 値の解釈に自信がない方は, The ASA Statement on p-Values: Context, Process, and Purpose を強くお勧めします。 ↩