はじめに
今回は, 和訳版の出ていなかった下のドキュメンテーションを和訳しながら実行していきます。(私の小言の方が多いかも。あまり逐語訳する気持ちはありません。)
https://jp.mathworks.com/help/parallel-computing/examples/plot-during-parameter-sweep-with-parfeval.html
事例:ローレンツ系
今回は以下の常微分方程式で表されるローレンツ系でのパラメタスイープを実行します。$\sigma,\rho,\beta$ はその系のパラメタを示します。
\begin{align}
\frac{\mathrm{d}}{\mathrm{d}t}x &= \sigma(y-z) \\
\frac{\mathrm{d}}{\mathrm{d}t}y &= x(\sigma - z) -y \\
\frac{\mathrm{d}}{\mathrm{d}t}z &= xy - \beta x
\end{align}
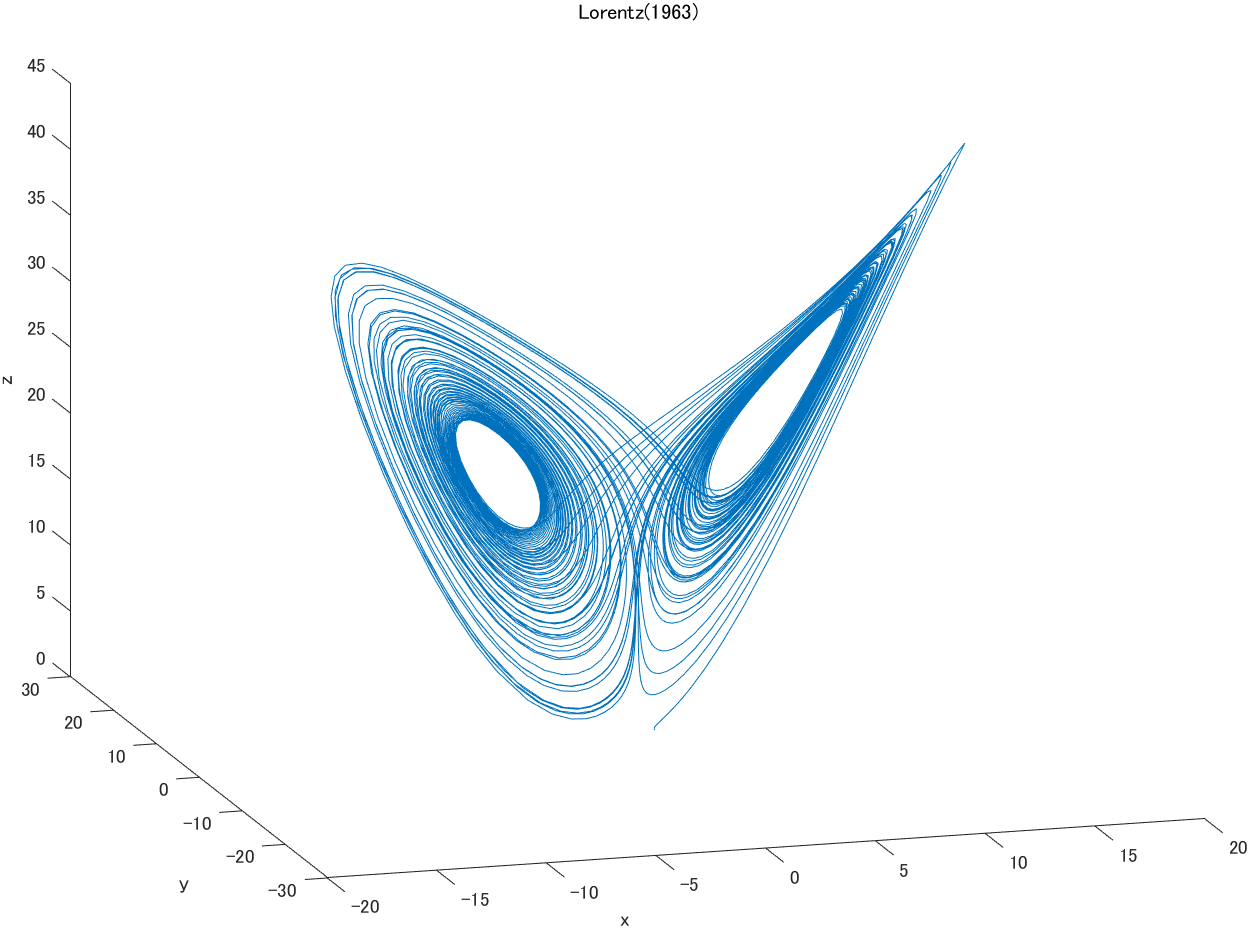
折角なので, Loretz(1963)1が想定した系を実装してみます。ソルバーは ode45 を使用しました。(普段から ode45 でやってみて, 良さげだったらヨシ!みたいにやってます。ここらへん勉強不足...)a の各行が上の数式の $x,y,z$ に対応しています。
sigma = 10;
beta = 8/3;
rho = 24.74;
f = @(t,a) [sigma*(-a(1) + a(2)); a(1)*(rho - a(3)) - a(2); a(1)*a(2) - beta*a(3) ];
[t,a] = ode45(f,[0 100],[1 1 1]); % [x0 y0 z0] = [1 1 1]
plot3(a(:,1),a(:,2),a(:,3))
xlabel('x'); ylabel('y'); zlabel('z')
title('Lorentz(1963)')
所望の図が得られました。
パラメタスイープを実行してみる
それでは,パラメタスイープ用の関数を作ってみます。パラメタのインデックス幅,パラメタ,キューを入力引数とし,最終到達点の z 座標を result に格納します。インデックス幅を指定する意味は後ほど。
function results = parameterSweep(first,last,sigma,rho,beta,Q)
results = zeros(last-first,1);
for ii = first:last-1
lorenzSystem = @(t,a) [sigma(ii)*(a(2) - a(1)); a(1)*(rho(ii) - a(3)) - a(2); a(1)*a(2) - beta*a(3)];
[t,a] = ode45(lorenzSystem,[0 100],[1 1 1]);
result = a(end,3); % z 座標を返す。
send(Q,[ii,result]); % キュー (DataQueue Object) を用いて,ワーカーからクライアントに結果を送る。
results(ii-first+1) = result;
end
end
パラメタスイープを実行する前に,座標軸も設定しておきましょう。今回は $\sigma, \rho$ を変化させてみて,どのような変化が起きるかを可視化してみます。
gridSize = 40;
sigma = linspace(5, 45, gridSize);
rho = linspace(50, 100, gridSize);
beta = 8/3;
[rho,sigma] = meshgrid(rho,sigma);
figure('Visible',true);
surface = surf(rho,sigma,NaN(size(sigma))); % z 座標を NaN にしておく。
xlabel('\rho','Interpreter','Tex'); ylabel('\sigma','Interpreter','Tex')
座標軸の設定ができたので,この上にプロットしていきます。まずは,parallel pool を起動し,DataQueue Object を作成します。
parpool; % parallel pool 起動
Q = parallel.pool.DataQueue
afterEach(Q,@(data) updatePlot(surface,data));
updatePlot 関数は以下の通りです。
function updatePlot(surface,data)
surface.ZData(data(1)) = data(2); % 上で NaN にしていた z 座標に代入する。
drawnow('limitrate'); % 更新のレートを 20 frames /sec にする。
end
上の createParameter 関数でインデックス幅をしていましたが,これはワーカーにロードするパラメタを分割するためです。parfeval はワーカーへのロードを分割した方が効率よく動作します。分割の目安に関しては,ドキュメンテーションでは「一つのタスクが,ジョブスケジューリングによるオーバーヘッドよりも十分大きい計算時間を費やすサイズ」で,「タスク数が,すべてのワーカーに割り当てられるだけある」と説明されています。(めっちゃ意訳してますが,分散処理のお決まりですね。)
ということで,$\sigma, \rho$ を以下のように分割し,パラメタスイープを実行します。
step = 100;
partitions = [1:step:numel(sigma), numel(sigma)+1];
f = parallel.FevalFuture; % ここ仕様変更(R2019b 時点)があったみたいで,公式から変更していますが,ただの事前割り当てです。
for ii = 1:numel(partitions)-1
f(ii) = parfeval(@parameterSweep,1,partitions(ii),partitions(ii+1),sigma,rho,beta,Q);
end
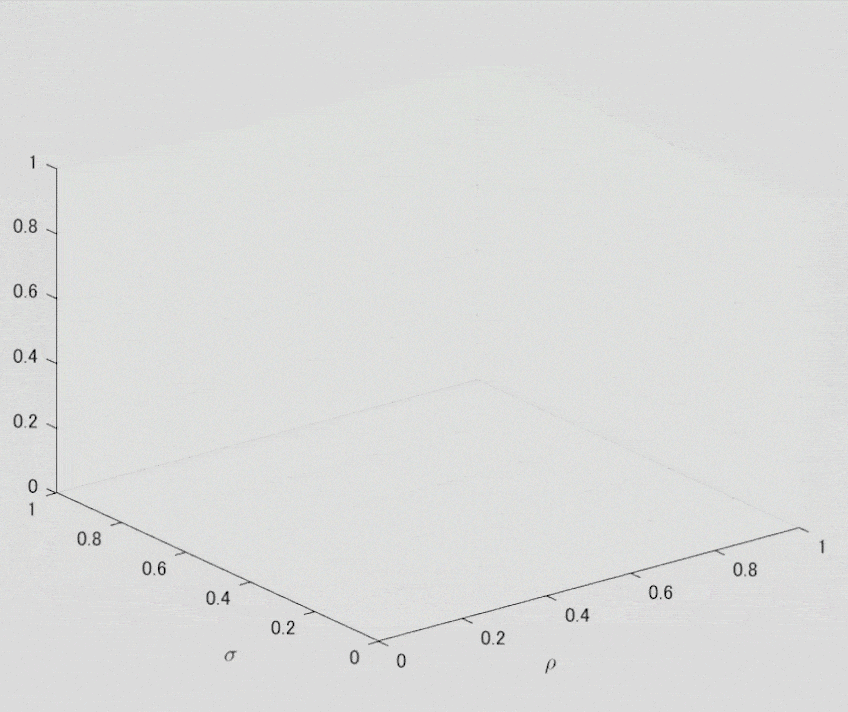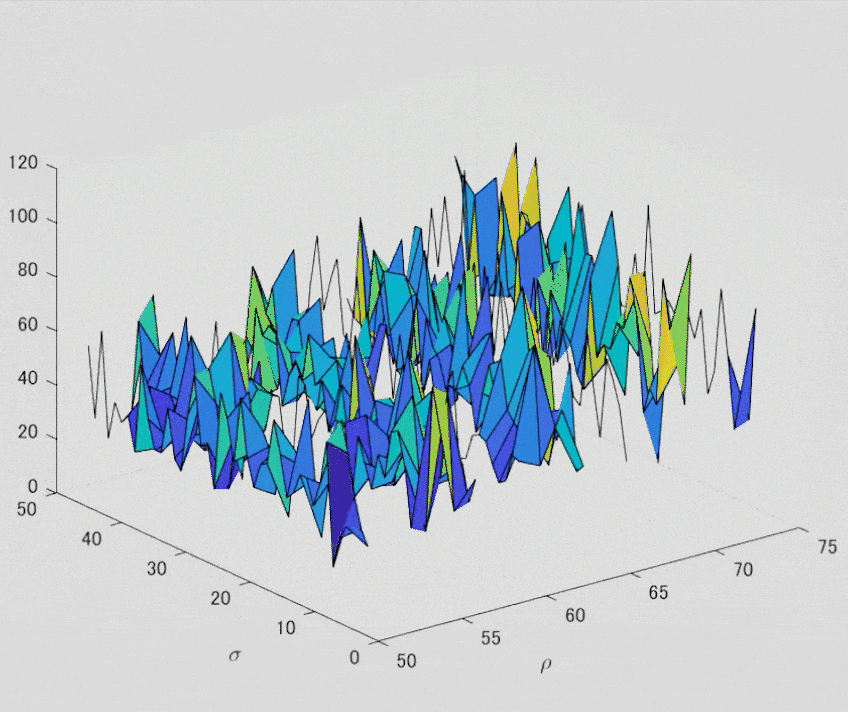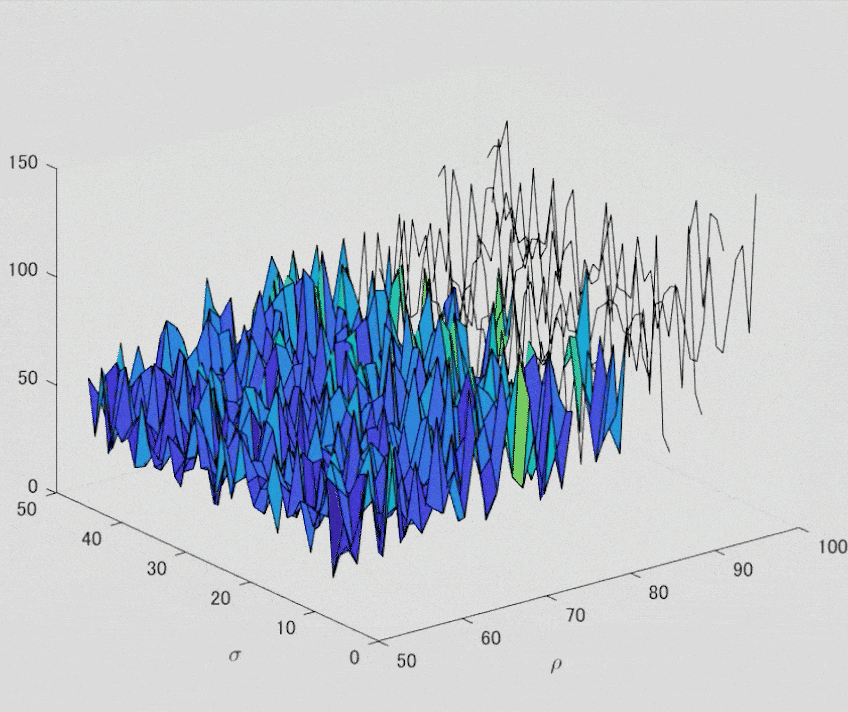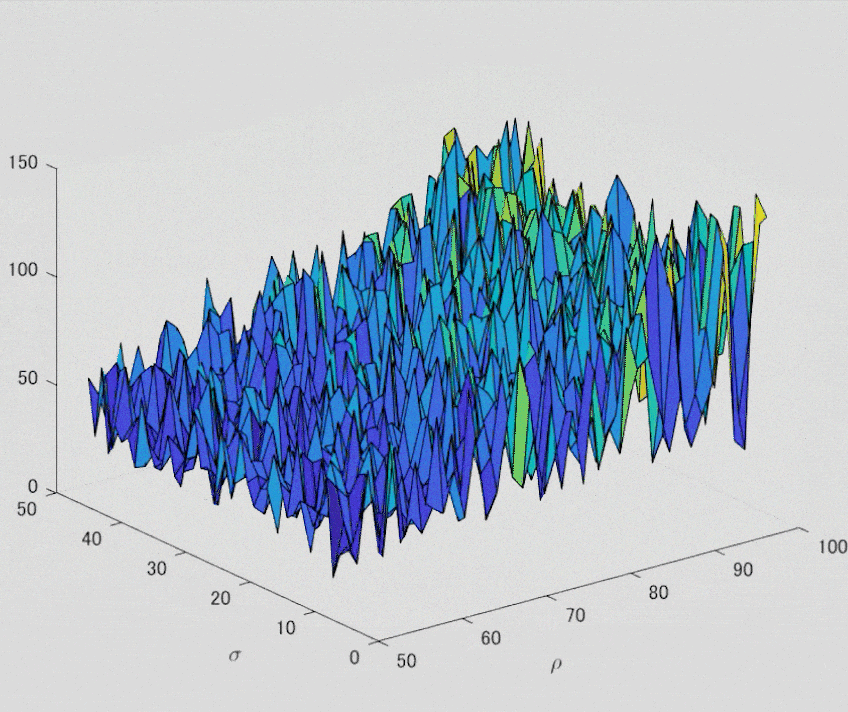
出力できました。ワーカー数 8 で実行しています。よく見ると, 4x2=8 ずつプロットが進んでいるのがわかりますね。(MATLAB でプロットを gif で出力する技を身に着けてないので,キャプチャ(苦笑))
wait(f); を入力すれば,f のタイマーが実行を終えるまでコマンドをブロックできるので,上の parfeval の結果に依存するようなコマンドのエラーを予防できます。
results = reshape(fetchOutputs(f),gridSize,[]);
contourf(rho,sigma,results)
xlabel('\rho','Interpreter','Tex')
ylabel('\sigma','Interpreter','Tex')
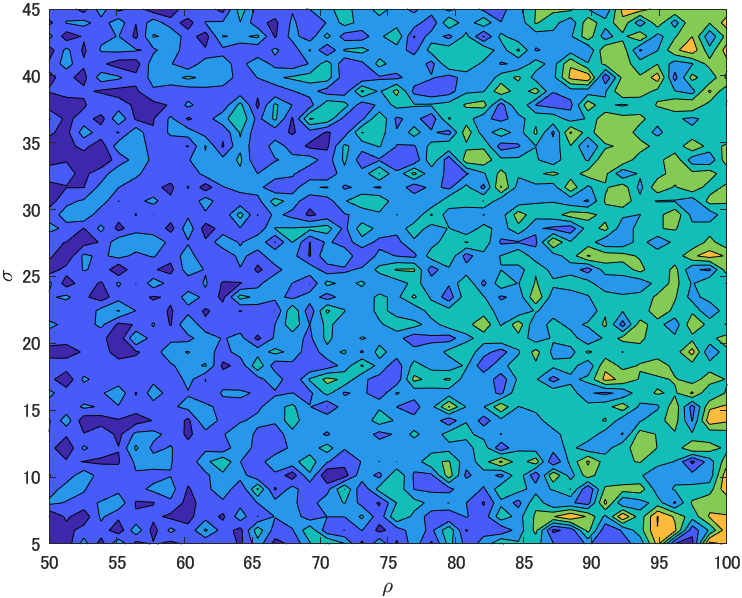
まあこれが何を示唆するかさっぱりなんですけどね。「やっぱカオスだねぇ,初期条件動かしたわけではないけど」ってことでいいのかな。 このドキュメンテーションが和訳されない理由がなんとなくわかる気がする。
まとめ
parfeval は事前に入力引数を分割してあげるとよいぞ。
-
E. N. Lorenz, “Deterministic Nonperiodic Flow,” Journal of Atmospheric Sciences, Vol. 20, No. 2, 1963, pp. 130-141. ↩