タイトルに興味を示していただきありがとうございます。
初めての記事のため読みづらいところがあると思いますが、ぜひ最後まで読んでいただきますと、ブラックジャックのルールや完璧にプレーイングするPythonプログラムの内容について理解していただけると思います。ちなみにPythonを学び始めてあまりたっていないのでクラスのところでとんちんかんなことを言ってる可能性があるので、その場合は指摘をお願いします。
20万円すった話と結論
では早速結論から申し上げたいと思います。ブラックジャックにおけるチートシートであるベーシックストラテジー(後述)通りの完璧なプレーイングをしても最後には必ず全持ち金が消え去ります。(縦:所持金 横:プレー回数)
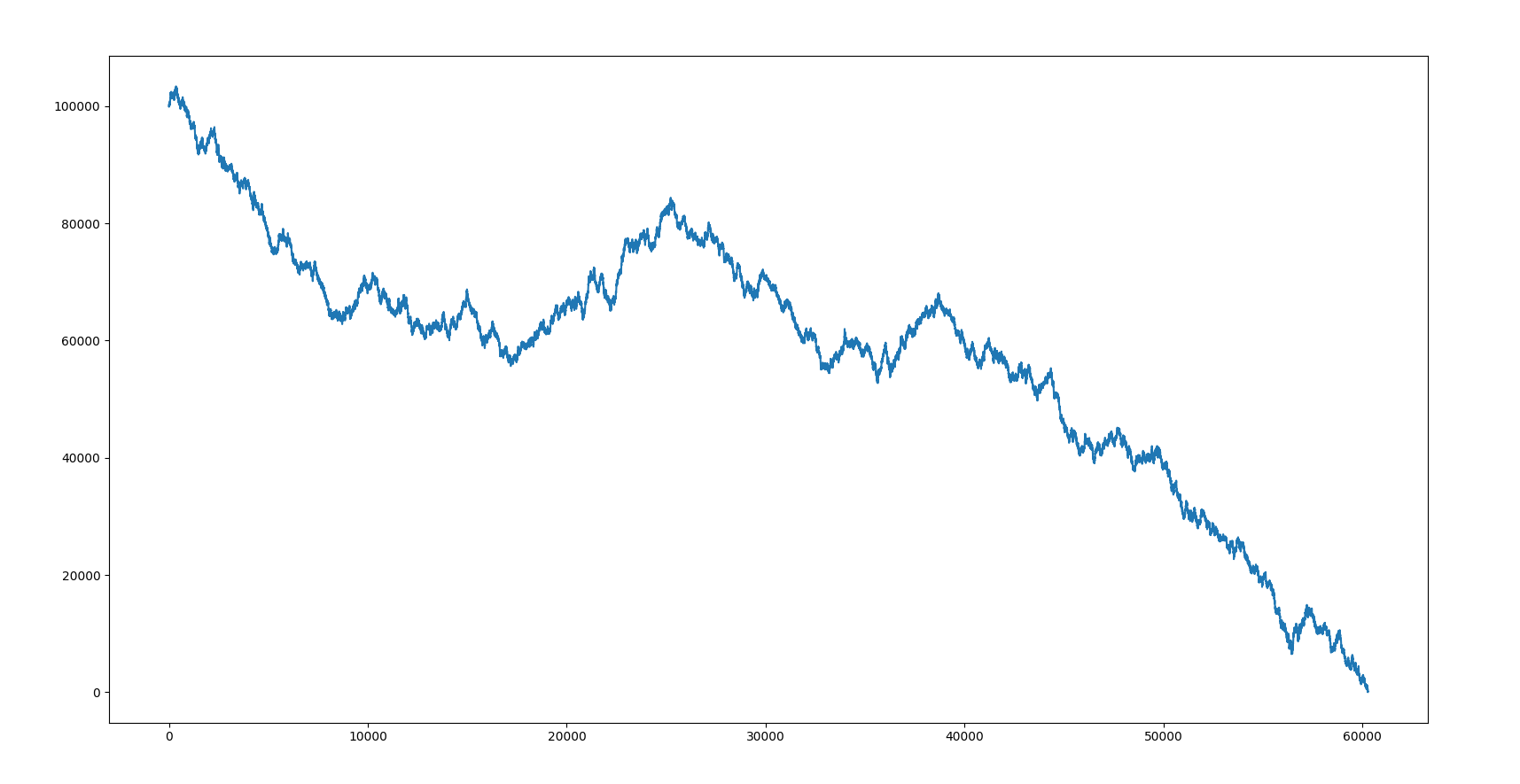
ギャンブルで一攫千金なんて甘い話は本当に存在しないらしいです。しかし著者がこれに気づくまでには結構時間がかかりました。。。
といいますのも実際にマカオやシンガポールのリアルなカジノを訪れて、毎回10万円の計30万円ほど利益を出していたからです。儲かっているのでは!と思われるかもしれませんが、調子に乗っていざ本場のラスベガスのカジノにて、よりハイベットで回していたところ3時間で50万の全軍事金を溶かしてしまいました。
今でも放心状態でカジノを出て、あれだけ輝いていたネオン灯がくすんでしまった景色を思い出せます。またその後のご飯は全部サブウェイに格下げしたのも苦い思い出です。
その後、2年間ほどギャンブルからは手を引いて堅実な生活をしていましたが、先日ふとラスベガスの完敗がたまたまとんでもなく運が悪かったのか、それともブラックジャックの仕組み的にいつかは絶対に負けることが決まっていたのかが気になりだしました。そこでPythonの脱初心者の意味合いを含めて、CUIベースのブラックジャックのゲームとベーシックストラテジーを完璧にプレーイングするプログラムを実装して検証してみました。
ブラックジャックのルールと完璧なプレーシングの意味
ブラックジャックのルールを全部詳細に説明しますと、それだけで違う記事が書けてしまうので簡潔にまとめてみました。ルール分かってるよって人はこの章中の完璧なプレーイング説明までとばしてください。
まず大原則としてこれだけを理解しておければいいことは、
・自分に配られたカードの目の合計が21以下でディーラーより大きければ勝ったことになり、掛け金分が上乗せされて戻ってきます。しかし21を超えてしまったらバースト扱いで掛け金が全没収されます。
・ディーラーは合計が17以上になるまでは絶対にカードを引き続けなければいけません。もしディーラーがプレイヤーより21に近ければ掛け金を全部没収することができます。しかしディーラー側も21を超えてしまったらバースト扱いになり、今度はプレイヤーの掛け金が倍になって払い戻されます。
・10以上の絵札カードはすべて値の10として扱い、エースは1か11扱いすることができます。2~9はそのままです。
・もしプレイヤーが最初に配られた2枚がエースと10以上のカードの場合、合計が21のためブラックジャックになり、掛け金分の1.5倍上乗せされ返ってきます
たったこれだけです。
ゲームの進行としましては、まず掛け金をかけたら、プレイヤーとディーラー互いに2枚配られます。しかしディーラーは1枚表のもう1枚は裏状態のため、ディーラーの正確な合計が分かりません。そこで常に先手のプレイヤーはディーラーの唯一表になっている1枚から推測して、スタンド(これ以上カードをいらない合図)をするまで以下の行動をとり続けないといけません(プレイヤーターン)。
・ヒット
もう1枚カードを引きたい
・(最初の2枚状態の時のみ)サレンダー
自分の最初の2枚が弱すぎるから降参する。だから掛け金を半分返して
・(最初の2枚状態の時のみ)ダブルダウン
どんなカードが来てもいいから1枚しか引かない。その代わり掛け金を倍にしてくれ
・(最初の2枚が同じ数字の時のみ)スプリット
それぞれに掛け金分を乗せるから、2枚を分割して独立した手として扱いたい。
そしてプレイヤーターンの間に合計が21を超えてしまった場合は、ディーラーがどんなに弱い手でも負け扱いになり掛け金ボッシュートです。
もしプレイヤーが21を超える前にスタンドした場合、ディーラーターンに入れ替わります。ここでは機械的にディーラーは17以上になるまでカードを引き続けます。もしここで21を超えたらプレイヤーの勝ちです。しかし17以上21以下の場合はプレイヤーとの目の合計勝負になり、21に近いほうが勝ちます。もし引き分けの場合は掛け金がそのまま返ってきます。これを1ゲームとして、プレイヤーが飽きるか軍資金が全部溶けるまで回していきます。もちろん連続スプリットやインシュランスといった細かいルールはまだありますが詳細を知りたい方はぜひ自分で調べてみてください。
次に軽く完璧なプレーイングについて解説していきます。先ほどのルールを読むと、じゃあ自分は21になるべく近づくようにカードを引いていけばいいのかと考えるかもしれませんがそれは場面によっては間違いです。なぜなら改めてディーラーターンの説明を読みますと、機械的に絶対17以上になるまで引き続けないといけないからです。つまりディーラーの合計が21を超えて自滅(バースト)するようにプレイヤーは立ち回ればいいのです。
確率の話になりますが、もしディーラーの2枚の合計が16だった場合、次に引いてくるカードが5以下になる確率はいくつでしょうか?トランプ1デッキ(52枚)の中には5以下のカードが20枚あります。つまり20/52=5/13です。逆に言えばディーラーがバーストする確率(5より大きいカード)は8/13になります。そこで自分の初期2枚合計が12、ディーラーが唯一表になっているのが6の場面を考えます(裏になっているカードは常に10と考えます、つまりディーラーの合計は16と仮定します)。自分が4/13の確率で先に行動して自滅するよりはスタンドして、ディーラーに8/13の確率でバーストしてもらったほうが確率的にいい動きであるといえます。このように自分が21に近くなくても、スタンドをしてディーラーに自滅してもらうのがブラックジャックにおいて最善手である場面がいくつか存在し、決まるとこの上なく気持ちいいです。
そして自分の合計とディーラーの表になっている目に応じて行うべき最善手を記したチートシートであるベーシックストラテジーチャートというものが存在します[1]。
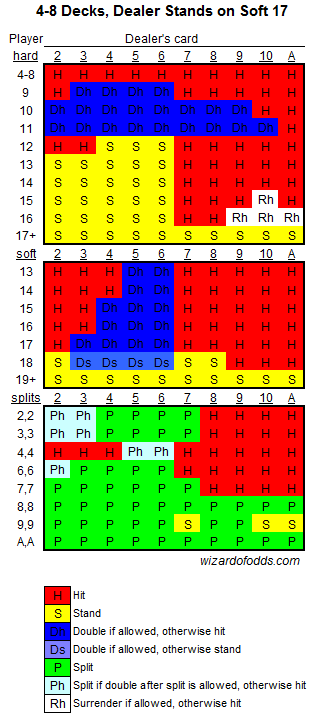
これを完全に暗記することでブラックジャックの中級者に仲間入りしたと言い張ることができます。しかし今回の記事においてベーシックストラテジーチャートの動きを完璧なプレーイングと呼ぶことにしておりますが、実際はさらにもう1段階複雑なカウンティングという技術があります。そのためブラックジャック上級者からすると完璧なプレーイングじゃないとツッコミたくなると思いますが我慢してください。だって実装が大変なうえカジノ側に見つかると出禁を食らうからモチベーションが出ませんでした。
コードの内容と結果
Qiitaを読んでいる層が、今更脱初心者のために書いた自分のコードから学ぶことは多分皆無だと思いますのでこちらには全コード載せませんし、解説もしません。興味がある方は自分のGithubを覗いてただければと思います(https://github.com/kkodio21/blackjack-game) 。
とりあえず苦労をしたところをいくつか挙げていきます。
オブジェクトを使用するかどうか
脱初心者のためにも、若干複雑と感じているクラスを使用してプレイヤーやディーラーの手を管理したいと意気込んでコーディングを考えていました。しかし途中でブラックジャックの性質上、配られる手をインスタンス化してもすぐ次のゲームではまた新しい手が配られるため恩恵がないと判断し、結局2次元配列を使用して進めていくことにしました。本当に脱初心者できているのかいまだによくわかっていないです。
エースの扱い
ブラックジャックにおいてはエースは状況に応じて1か11扱いすることできます。つまり自分の2枚の手札がエースと7の場合は手札合計を8か18と扱うことが来ます。もしここでディーラーの表が10の場合、基本的には引くべきですがもしここで3枚目に8を引いた場合は26ではなく、エースを1のほうで扱い合計16で進めていきます。そしてこの状況に応じてエースの値を変えなければいけないという処理が難しく、最終的には最初にエースは値の11として、引いてくるデッキに保存しました。そしてもしエースを持っている状態で21を超えてしまったら自分の手に-10を追加することでうまく実行できるようにしました。そのためプレイヤーの手を表示した場合に、実際のブラックジャックではあり得ない-10という値が出てきてしまいますが、遊ぶ目的ではなく検証のためいいのではとこの方法で実装しました。もちろん使いづらいですがブラックジャックをCUI状態で遊べます。
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
連続スプリット
ブラックジャックではたまに連続で同じ数字が来ることがあります。そして数字によっては連続でスプリットをするべき場面があります。例えば2枚とも8だった場合は絶対にスプリットを選ぶべきですが、もし独立した手にまた8が来てしまったらさらにスプリットをして、保有している手を3つにするといった場面が発生することがあります。著者も一度連続でエースが4回来て、連続スプリットで自分の目の前に4つの手があったときはパニクりました。なんせ最初の掛け金の4倍をかけたことになり、勝てば一攫千金、負ければ大損をしてしまうからです。結果はご想像にお任せします。
こちらも最初どのように実装するべきか悩みましたが、2次元配列に新しくその数字を要素として追加し、元の配列ではその数字を消せばいいだけでした。
if地獄
ゲームをしっかり実装できたところで、次は上の図のベーシックストラテジーチャートの動きをなぞるコードを書く必要性がありました。これは特段複雑ではなかったのですが、色ごとにif statementを書く必要性があり、ただただ条件分けを書いていくのが単調でつらかったです。
if sum(selfcards[a])==11 or sum(selfcards[a])==10 and oppcards[0]<10:#double up
pickself(selfcards,a)
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
selfcards[a].append("up") # if last is up dont hit
elif sum(selfcards[a])==9 and (oppcards[0]<7 and oppcards[0]>2):
pickself(selfcards, a)
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
selfcards[a].append("up") # if last is up dont hit
elif (selfcards[a][0]==11 and selfcards[a][1]==6 or selfcards[a][0]==6 and selfcards[a][1]==11)\
and (oppcards[0]<7 and oppcards[0]>2):
pickself(selfcards, a)
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
selfcards[a].append("up") # if last is up dont hit
elif (selfcards[a][0]==11 and selfcards[a][1]==8 or selfcards[a][0]==8 and selfcards[a][1]==11)\
and oppcards[0]==6:
pickself(selfcards, a)
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
selfcards[a].append("up") # if last is up dont hit
elif (selfcards[a][0] == 11 and selfcards[a][1] == 7 or selfcards[a][0] == 7 and selfcards[a][1] == 11) \
and oppcards[0] < 7:
pickself(selfcards, a)
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
selfcards[a].append("up") # if last is up dont hit
elif (selfcards[a][0]==11 and (selfcards[a][1]==5 or selfcards[a][1]==4) or (selfcards[a][0]==5 or selfcards[a][1]==4)\
and selfcards[a][1]==11) and (oppcards[0]<7 and oppcards[0]>3):
pickself(selfcards, a)
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
selfcards[a].append("up") # if last is up dont hit
elif (selfcards[a][0] == 11 and (selfcards[a][1] == 3 or selfcards[a][1] == 2) or (selfcards[a][0] == 3 or selfcards[a][1] == 2)\
and selfcards[a][1] == 11) and (oppcards[0] < 7 and oppcards[0] > 4):
pickself(selfcards, a)
if 11 in selfcards[a] and sum(selfcards[a]) > 21:
selfcards[a].append(-10)
selfcards[a].append("up") # if last is up dont hit
else:
selfcards[a].append(0)
こんな感じでだいたい12時間ぐらいかけて、コーディングを終えました。そしてついにブラックジャックで完璧なプレーイングをしたら儲かるのか検証をする時が来ました。最初の持ち金は100000で毎回の掛け金を100にして実行しました。するとターミナルにこのような文字が目まぐるしく表れました。
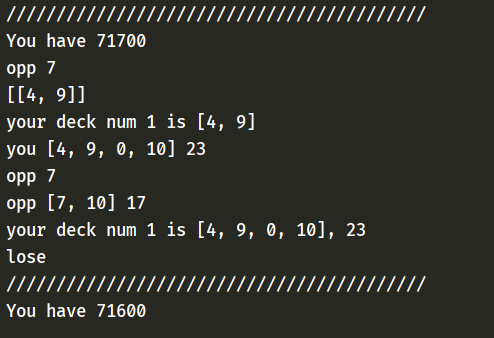
色々表示されていますが重要なのは You have 71600。 うーん確実に最初の100000から減っている。。。 その後何度かリセットして実行してみましたが、最終的にすべてが所持金0になってしまいました。そこでMathplotlibを使用して、減り具合や何回目のプレー回数で0になるか検証してみたところ以下のグラフのようになりました。(縦:所持金 横:プレー回数)
1

これらのグラフから主に2つのことが読み取れるかと思います。1つはブラックジャックは遊べば遊ぶほど損をすることです。今回の検証内容でもあった完璧なプレーイングの元ブラックジャックで儲けることができるに対しては完全にノーですね。持ち金の1000分の1を賭け続けても30000~60000手らへんで所持金が0になります。
2つ目は必ずどこかで所持金が一時的に増えるタイミングがあることです。この一時的に増えるが重要で、たまたまそこの数回で儲かり続ける流れが来ただけで、長い視点で見ると最終的には損をします。特に1つ目のグラフの20000手らへんからの上昇は目を見張るところがあります。実際に私もこのような上昇が最初の時にたまたま来ていただけで、このグラフの結果と同じように最終的には所持金が0になっています。さすがにハイリスクで回していたとはいえ200手ぐらいで全ロスしているので運が悪いほうではあると思いますが。
考察
ここまで読んでいただきありがとうございました。最後になぜブラックジャックが(データでは否定してしまいましたが)魅力的で世界中に愛されているギャンブルかについて軽く考察していきます。
それはズバリ人間は愚かで微妙な変化には気づかないからです。何を言ってんだと思うかもしれませんが、データがそれを体現しています。まずブラックジャックは1プレーするのに平均1分ほどかかるかといわれています。つまり持ち金の100分の1をかけ続けたとしても、全部溶かすのに約5000手、つまり80時間ほどかかります。おそらく連続でこの時間を遊ぶ人はいないと思います。そこで仮に2時間遊ぶとして持ち金は1/40=2.5%しか減らないのです。この2.5%は感覚的には認知しづらい値かと思います。特にカジノではたまに動く大金のせいで一種の興奮状態になっており、2.5%の損は気にしなくなってしまいます。また金銭感覚が鈍るようわざとチップを使用しているので余計に損を認知しにくくしてます。うってつけにたまに大勝ちする要素があれば、これはブラックジャックに魅力を感じて依存症になる人が出てきてもおかしくないかと思います。損は感じず、儲けは印象に残ります。人は愚かですね。
以上からブラックジャックはベーシックストラテジーチャート通りの完璧なプレーイングをしても決して儲かることがなく、おそらく自分は今後リアルマネーで遊ぶことはないかと思います。
最近ポーカーをリアルマネーでやりたい欲が出てきてるのは秘密ですが。
KODIO
参考文献
[1] 4-Deck to 8-Deck Blackjack Strategy, https://wizardofodds.com/games/blackjack/strategy/4-decks/

