はじめに
この記事は、JavaScriptの学習をする中で気になったNumber.EPSILONについての解説を記載しています。
MDNの内容をもとに、筆者が自分なりに理解した内容を記載します。
Number.EPSILONとは
JavaScriptにおけるNumberオブジェクトの静的プロパティであり、MDNでは以下のように記載されています。
Number.EPSILON プロパティは、1 と 1 より大きな最小の浮動小数点数の差を表します。
値
$2^{-52}$、またはおよそ 2.2204460492503130808472633361816E-16。
解説
Number.EPSILON は、1 と数値形式で表現できる次に大きな数値との差です。これは、倍精度浮動小数点数形式では仮数部を 52 ビットでしか表現できず、最低ビットは $2^{-52}$ で表されるためです。
上記より、Number.EPSILONはとても小さい値であることがわかります。
1E-16
= $1×10^{-16}$
= $\frac{1}{10,000,000,000,000,000}$
= 1京分の1
なぜこの数値なのか
Number.EPSILONは「1 と 1 より大きな最小の浮動小数点数の差」を表すそうですが、なぜ$2^{-52}$なのでしょうか。
仮数部を 52 ビットでしか表現できず
この辺りにヒントはありそうですが、この$2^{-52}$という値についてもう少し深堀りしたいと思います。
JavaScriptの数値 (Number) 型
MDNのJavaScript標準組み込みオブジェクト-Numberのページでは、以下の説明文が記載されています。
数値のエンコーディング
JavaScript の数値 (Number) 型は IEEE 754 の倍精度 64ビットバイナリー形式であり、 Java や C# の double のようなものです。つまり、小数値を表しますが、格納される数値の大きさと精度には制限があります。とても簡単に説明すると、IEEE 754 の倍精度数は、3 つの部分を表すのに 64 ビットを使用します。
- 1 ビットの符号(sign, 正の数または負の数)
- 11 ビットの指数部(exponent, -1022 から 1023)
- 52 ビットの仮数部(mantissa, 0 と 1 の間の数値を表す)
仮数部(significand とも呼ばれる)は、実際の値を表す部分(有効数字)です。指数は、仮数を乗じるべき 2 のべき乗です。科学的記数法として考えると、次のようになります。
Number = $(−1)^{sign}⋅(1+mantissa)⋅2^{exponent}$

図1:Wikipediaより引用
もう少し理解しやすくするために考えてみます。
浮動小数点数0.375
最初に、浮動小数点数の0.375をIEEE 754 の倍精度 64ビットバイナリー形式で表すとどうなるか考えてみます。
まず、0.375を2進数に変換します。
0.375=0.011_2
10進数小数の2進数変換方法の解説は省略します。
次に、$0.011_2$を正規化します。
$0.011_2$の整数部が1になるように正規化すると次のようになります。
0.011_2
= 1.1 × 2^{-2}
上記より、「Number = $(−1)^{sign}⋅(1+mantissa)⋅2^{exponent}$」に当てはめると次のように表せます。
1.1 × 2^{-2} = (−1)^{0}⋅(1+0.1)⋅2^{-2}
ここでポイントなのが指数部(exponent)です。
MDNでは詳しく記載されていませんが、IEEE 754では、ビット列で表した場合の実際の指数部の値に対して、バイアス値の「1023」を足すことで、ビット列で表した際に指数部が常に正の数となるように定められています。1
つまり、上記の数式には、2の指数部に1023があらかじめ足されていると考えられるため、
以下のようにも表すことができます。
(−1)^{0}⋅(1+0.1)⋅2^{-2} = (−1)^{0}⋅(1+0.1)⋅2^{1021-1023}
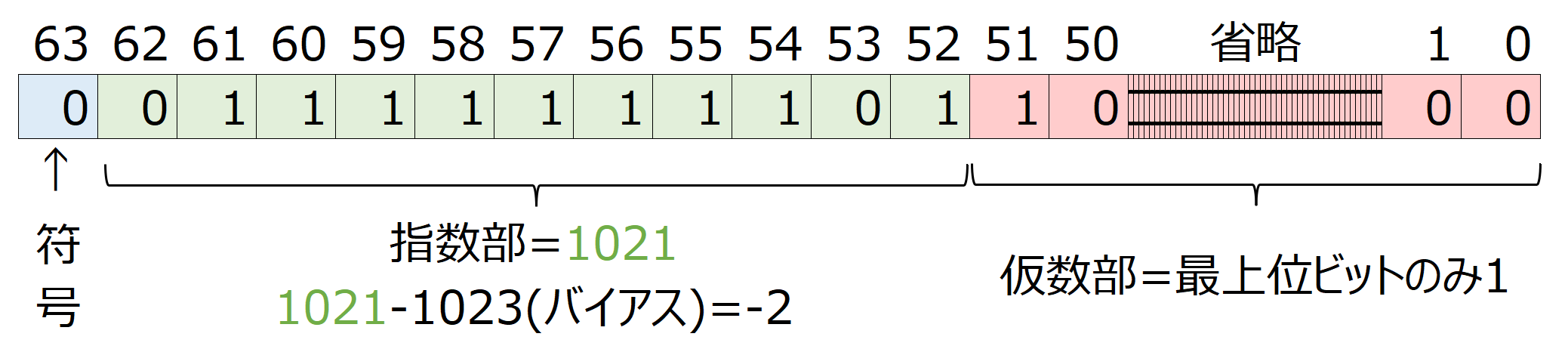
以上から、浮動小数点数の0.375をIEEE 754 の倍精度 64ビットバイナリー形式のビット列で表すと以下のようになります。
整数の1
次に、整数の1をIEEE 754 の倍精度 64ビットバイナリー形式で表すとどうなるか考えてみます。
「Number = $(−1)^{sign}⋅(1+mantissa)⋅2^{exponent}$」に当てはめると、1は次のように表せます。
1 = (−1)^{0}⋅(1+0)⋅2^{0}
指数部には1023のバイアスがかかっているため、以下のようにも表せます。
1 = (−1)^{0}⋅(1+0)⋅2^{(1023-1023)}
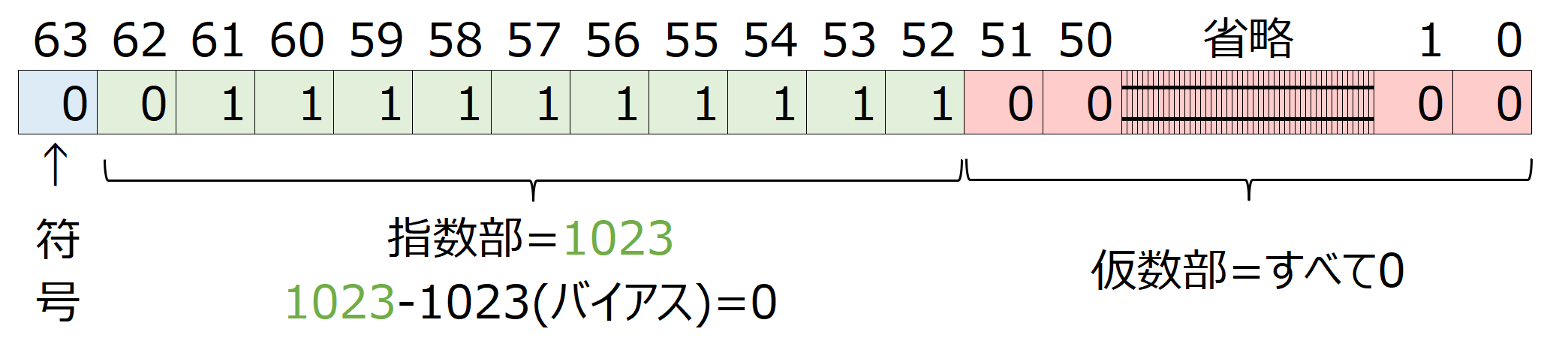
上記より、整数1をIEEE 754 の倍精度 64ビットバイナリー形式のビット列で表すと以下のようになります。
このとき、仮数部の0は52ビットがすべて0、つまり、0が52個分並んでいると考えることができます。
1=(−1)^{0}⋅(1+0.0000000000000000000000000000000000000000000000000000)⋅2^{(1023-1023)}
1 より大きな最小の浮動小数点数
では、上記をもとに、1 より大きな最小の浮動小数点数をIEEE 754 の倍精度 64ビットバイナリー形式で表すとどうなるか考えてみます。
- 符号
- 1より大きくないといけないため、正の数である必要があります。つまり符号のビットの値は0です。
- 指数部
- 指数部が1大きくなると、$2^{(1024-1023)}$=$2^{1}$=2となり、数式全体で1の2倍=2以上になってしまいます。よって、指数部は増減なしの0のままである必要があります。
残ったのは仮数部です。
仮数部は52ビットで表されているため、「1 より大きな最小の浮動小数点数」を表そうとすると最下位ビットを1増やせばよさそうです。
(−1)^{0}⋅(1+0.0000000000000000000000000000000000000000000000000001)⋅2^{(1023-1023)}
これをビット列で表すと次のようになります。
1 と 1 より大きな最小の浮動小数点数の差
今まで求めた結果より、
1 と 1 より大きな最小の浮動小数点数の差は、IEEE 754 の倍精度 64ビットバイナリー形式のビット列で表した際の仮数部の差「0.0000...(中略)...0001」ということが分かります。
0.0000...(中略)...0001を正規化すると次のようになります。
0.0000000000000000000000000000000000000000000000000001=1 × 2^{-52} = 2^{-52}
これがNumber.EPSILONの正体です。
「1 と 1 より大きな最小の浮動小数点数の差」のことを計算機イプシロンと呼び、Number.EPSILONの名前の由来はここから来ているようです。
Number.EPSILONは何のために存在するのか
MDNでは、JavaScript上の演算において0.1 + 0.2 は 0.3 と正確に等しくならないことが紹介されており、演算結果が 1 程度の大きさであれば、通常 Number.EPSILON 定数がエラーに対する妥当な閾値となると記載されています。
console.log(0.1 + 0.2); // 0.30000000000000004 console.log(0.1 + 0.2 === 0.3); // false
function equal(x, y) { return Math.abs(x - y) < Number.EPSILON; } const x = 0.2; const y = 0.3; const z = 0.1; console.log(equal(x + z, y)); // true
理解を深める上で以下の記事が非常にわかりやすく参考になりましたのでご紹介します。
また、JavaScript上の演算結果では、確かに0.1 + 0.2 ≠ 0.3であることが確認できました。
console.log(0.1 + 0.2); // 0.30000000000000004
console.log(0.1 + 0.2 === 0.3); // false

図2:筆者のGoogle Chrome(バージョン: 131.0.6778.109)の開発者ツールより
まとめ
- JavaScriptにおける
Number.EPSILONの値は$2^{-52}$(およそ 2.2204460492503130808472633361816E-16) - $2^{-52}$となる理由は、JavaScriptの数値 (Number) 型は IEEE 754 の倍精度 64ビットバイナリー形式であるため