【NeurIPS 2024 Spotlight 論文】Acoustic Volume Rendering (AVR)を読んで動かしてみた

はじめに

NeurIPS 2024 Spotlightに採択された論文「Acoustic Volume Rendering for Neural Impulse Response Fields」の解説を行います。

本論文のテーマは「音響インパルス応答（IR: Impulse Response）生成」です。インパルス応答とは、ある位置の音源から放たれた瞬間的な音（インパルス）が、別の位置のマイクにどのように届くかを記録したもので、反射や回折、吸収といった空間音響特性を反映します。IRと任意の音声信号を畳み込むことで、場所による音の聞こえ方の違いをリアルに再現することができます。音響IRは、例えば、VR空間での音響環境構築、補聴器製作時の音響シミュレーション、ロボットの音環境認識やナビゲーション機能開発に利用されています。

従来のIRを求める方法として、物理シミュレーションによって構築する手法や、深層学習ベースで直接予測する手法が提案されてきました。特にNeurIPS 2022に採択されたNeural Acoustic Fields (NAF)、INRASなどは、NeRF（Neural Radiance Fields）に着想を得て、ニューラルネットワークを用いて「空間上のIR分布」を構築する代表的な研究です。

しかし、これらの手法には

• 位相成分の精度が低く、波形の整合性に欠ける
• 音波の伝播特性（遅延・減衰など）が明示的に扱われていない

といった課題が残されていました。

本論文では、こうした問題に対処するために、NeRFでも使用されているVolume Renderingの枠組みを音響に応用し、時間遅延や方向性、エネルギー減衰を考慮した新しい手法「Acoustic Volume Rendering (AVR)」を提案しています。

さらに、既存の音響シミュレーション環境では到達時間や位相に大きな誤差があることを指摘し、より高精度なIR生成を可能にする物理ベースの音響シミュレータ「AcoustiX」も併せて提案しています。

本記事では、AVRやAcoustiXの理論、従来手法との違い、実験結果を解説するとともに、実際に自分で動かしてみた結果を載せています。

目次

• 1. AVRとは何か？
  • 1.1 従来手法の課題
  • 1.2 AVRの理論
  • 1.3 AVRの損失関数
• 2. AcoustiXとは何か？
  • 2.1 従来手法の課題
  • 2.2 AcoustiXのベースエンジン: Sionna ray tracing
  • 2.3 AcoustiXによる拡張
• 3. 実験と評価
  • 3.1 実データセットでの生成IR精度
  • 3.2 シミュレーションデータセットでの生成IR精度
  • 3.3 音響場及び波形の可視化
  • 3.4 ゼロショットのバイノーラル音響生成
• 4. 公式ソースコードで実験してみた

1. AVRとは何か？

1.1 従来手法の課題

近年、深層学習による音響インパルス応答（IR）生成として、NeRFに着想を得たNAFやINRASといった手法が注目されています。
これらの手法は、ニューラルネットワークを用いて、音源及びマイクの座標・周波数・時刻からIRを直接予測しており、古典的な補間手法と比べて高精度なIR生成ができることを示しました。

しかし、音波の物理的性質である時間遅延や位相整合性、減衰を明示的に扱わないため、位相が正確に再現されず、また、学習データに過剰に適合してしまうことで、音響場全体の整合性が損なわれる、という課題がありました。

---

1.2 AVRの理論

本論文で提案された Acoustic Volume Rendering（AVR） は、上記の課題を解決するために、NeRFのVolume Renderingの枠組みを音響信号に応用した手法です。AVRでは、ニューラルネットワークで空間内の密度場と信号場をモデリングし、物理的整合性を保ちながらIRを生成します。

まず、AVRでは、マイクを中心とした球面から放射状のレイ（ray）を考え、レイ上で観測される音響信号をニューラルネットワークでモデリングします。

$$
F_Θ : (p, \omega, p_e, \omega_e) \rightarrow (\sigma, s(t)) \tag{3}
$$

• $p$: レイ上の空間中の点
• $\omega$: マイクから点$p$の方向
• $p_e$: 音源位置
• $\omega_e$: 音源の向き
• $\sigma$: 音響密度
• $s(t)$: 点 $p$ から方向マイク方向に向かって放射される音響信号

次に、遅延を考慮しながら、同じレイ上の各点での音響信号を足し合わせることで、以下のように方向 $\omega$ からマイク位置 $p$ に届く信号 $h_\omega(t)$を計算します。

$$
h_\omega(t) = \frac{1}{tv} \int_{u_n}^{u_f} L(u) \sigma(p(u)) s\left(t - \frac{u}{v}; p(u), \omega\right) du \tag{4}
$$

$$
L(u) = \exp\left( -\int_{u_n}^{u} \sigma(p(x)) dx \right)
$$

• $p(u) = p + u \cdot \omega$: レイ上の点
• $v$: 音速
• $u$: レイ上でのマイクからの距離
• $u_n$: $u$の最小値
• $u_f$: $u$の最大値
• $\frac{1}{tv}$: 距離によるエネルギー減衰項
• $L(u)$: 透過率

最後に、球面から放射状に考えた全レイからの音響信号を足し合わせ、最終的なインパルス応答 $h(t)$ を得ます。足し合わせる際、$G(\omega)$によってマイクの指向性を考慮します。

$$
h(t) = \int_{\Omega} G(\omega) h_\omega(t) d\omega \tag{5}
$$

• $G(\omega)$: マイクの指向性（ゲインパターン）
• $\Omega$: 球面全体

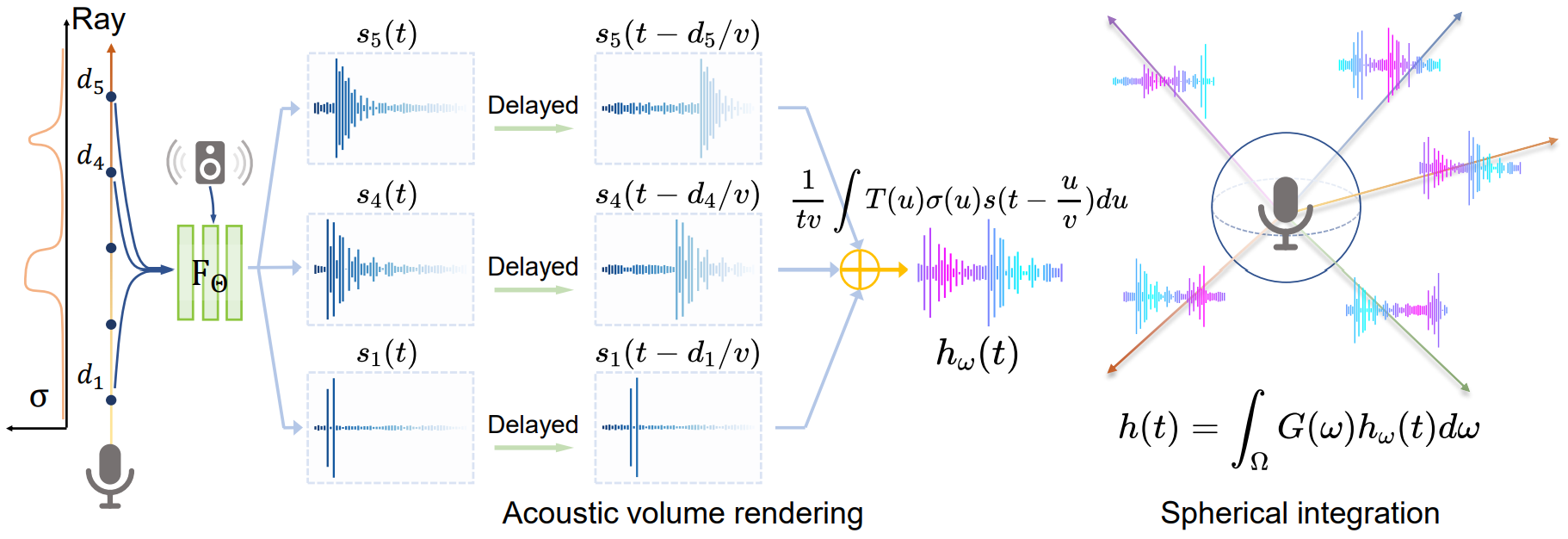
このようにAVRでは、Volume Renderingの考え方を用いることで、物理法則（遅延・減衰・方向性）を考慮して、IR生成を行っています。上記の流れを図で表すと以下（論文 Figure 3）のようになっています。

なお、実装では式(3)のニューラルネットワークの計算後、FFTして周波数領域にした後、式(4)(5)の積分計算を行っています。

具体的には、以下のようになります。

$$
H_\omega(f) = \frac{1}{tv} \sum_{u_n}^{u_f} \sigma(p(u)) S(f; p(u), \omega) \cdot e^{-j 2\pi f \frac{u}{v}} \tag{4'}
$$

• $S(f; p(u), \omega)$: 点 $p(u)$ における信号の周波数表現
• $e^{-j 2\pi f \frac{u}{v}}$: 時間遅延 $\frac{u}{v}$ に対応する位相シフト

$$
H(f) = \sum_{i=1}^{N_{\text{rays}}} G(\omega_i) H_{\omega_i}(f)\tag{5'}
$$

$$
N_{\text{rays}} = N_\theta \times N_\phi \times N_r
$$

• $N_\theta$: 方位角のサンプリング数
• $N_\phi$: 仰角のサンプリング数
• $N_r$: 距離のサンプリング数

---

1.3 AVRの損失関数

AVRでは、時間領域と周波数領域の両方で損失関数を定義し、学習を行っています。

特に周波数領域では、時間領域に比べて変化が滑らかであるため、微小なずれに対して損失値が過度に敏感になりにくく、学習が安定しやすいという利点があります。
そのため、AVRでは周波数領域での損失を重視しています。

---

記号の定義

• $h[n]$: 時間領域における生成インパルス応答
• $h^*[n]$: 時間領域における正解インパルス応答
• $H[f]$: 周波数領域における生成インパルス応答
• $H^*[f]$: 周波数領域における正解インパルス応答
• $|H|$: 複素スペクトルの振幅
• $\angle H$: 複素スペクトルの位相

---

損失関数に含まれる項

名称	定義式	説明
time domain loss	$ L_{\text{time}} = | h - h^* |_1 $	音声波形のずれを表す
energy loss	$L_{\text{energy}} = \frac{1}{2T} \sum_{i=1}^{2T} | D_E(\tilde{R}_Q)_i - D_E(R_Q)_i |_1$ $\cdot 1[D_E(R_Q)_i \ne 0]$	エネルギー減衰特性のずれを表す
spectral loss	$ L_{\text{spec}} = | \text{Re}(H) - \text{Re}(H^*) |_1$ $+ | \text{Im}(H) - \text{Im}(H^*) |_1 $	複素スペクトルのずれを表す
magnitude loss	$ L_{\text{amp}} = | |H| - |H^*| |_1 $	複素スペクトルの振幅のずれを表す
phase loss	$ L_{\text{phase}} = | \cos(\angle H) - \cos(\angle H^*) |_1$ $+ | \sin(\angle H) - \sin(\angle H^*) |_1 $	複素スペクトルの位相のずれを表す
multi-resolution STFT loss	$ L_{\text{aux}}(G) = \frac{1}{M} \sum_{m=1}^{M} L^{(m)}_s(G) $	複数解像度での周波数構造のずれを表す

---

補足説明

• multi-resolution STFT loss
  Parallel WaveGAN で提案された損失関数で、音声波形の周波数構造を複数解像度で学習させます。
  様々なSTFTのパラメータ（FFT size、window size、frame shift）でそれぞれのSTFT lossを計算し、平均を取ることで求められます。
  複数解像度でのSTFT損失を合算することで、全体的な周波数構造と局所的な周波数構造をまとめて学習させ、音声波形に戻した際に妥当な形になるよう促進しています。

  $$
  L_{\text{aux}}(G) = \frac{1}{M} \sum_{m=1}^{M} L^{(m)}_s(G)
  $$

  • $M$: STFTパラメータのパターン数
  • $L^{(m)}_s$: STFT loss

  L_s(G) = \mathbb{E}_{z \sim p(z),\ x \sim p_{\text{data}}} \left[ L_{\text{sc}}(x, \hat{x}) + L_{\text{mag}}(x, \hat{x}) \right]
  

  • $\hat{x} = G(z)$: 生成波形
  • $x$: 正解波形
  • $L_{\text{sc}}$: spectral convergence loss
  • $L_{\text{mag}}$: log STFT magnitude loss

  $$
  L_{\text{sc}}(x, \hat{x}) = \frac{ | | \text{STFT}(x) | - | \text{STFT}(\hat{x}) | |_F }{ | | \text{STFT}(x) | |_F }
  $$

  $$
  L_{\text{mag}}(x, \hat{x}) = \frac{1}{N} \left| \log |\text{STFT}(x)| - \log |\text{STFT}(\hat{x})| \right|_1
  $$

  • $N$: STFTスペクトルの要素数

• energy loss
  FEW-SHOTRIR で提案された損失関数で、インパルス応答の時間的なエネルギー減衰特性を学習させます。
  波形の時間的な減衰や包絡線の形状を最適化するための損失です。

  STFTのスペクトログラムを周波数方向に加算して全帯域のエネルギー包絡線を取得し、Schroederの後方積分によりエネルギー減衰曲線を求めます。そして、減衰曲線の差を評価します。

  L_{\text{energy}} = \frac{1}{2T} \sum_{i=1}^{2T} \left\| D_{\mathcal{E}}(\tilde{R}_Q)_i - D_{\mathcal{E}}(R_Q)_i \right\|_1 \cdot \mathbb{1}[D_{\mathcal{E}}(R_Q)_i \ne 0]
  

  • $\tilde{R}_Q$：生成STFTスペクトログラム
  • $R_Q$：正解STFTスペクトログラム
  • $D_{\mathcal{E}}(\cdot)$：Schroeder積分により得られるエネルギー減衰曲線
  • $T$：時間方向のウィンドウ数

---

全体の損失関数

最終的な損失関数は、各損失項を重み付きで線形結合した以下の形となります：

$$
L_{\text{total}} = L_{\text{spec}} + \lambda_{\text{amp}} L_{\text{amp}} + \lambda_{\text{phase}} L_{\text{phase}} + \lambda_{\text{time}} L_{\text{time}} + \lambda_{\text{stft}} L_{\text{stft}} + \lambda_{\text{energy}} L_{\text{energy}} \tag{13}
$$

---

このように、AVRでは様々な観点からふくすうの損失を設計し、物理整合性のある高精度なIR生成を実現しています。

2. AcoustiXとは何か？

2.1 従来手法の課題

IRを深層学習する際の学習データとして、実データセットとシミュレーションデータセットがあります。しかし、十分な規模・多様性を持った実データセットは限られており、代表的なものに MeshRIR や Real Acoustic Fields (RAF) がある程度です。

そのため、多くの研究では SoundSpaces などのシミュレータによって生成されたデータセットが主に利用されています。

しかし、SoundSpacesなどの既存シミュレータでは、IRの位相や到達時間の誤差が大きく、実世界の音響特性を正確に反映できていませんでした。
そこで、電波のシミュレータであるSionna ray tracingを音波に拡張し、位相や到達時間の正確性を向上させたシミュレータAcoustiXを本論文で提案しています。

上記の図（論文 Figure 2）は、SoundSpacesとAcoustiXにおける到達時間の誤差を比較したものです。特に、スピーカーとマイクの距離が短い場合、SoundSpacesでは到達時間の誤差が顕著であるのに対し、AcoustiXは一貫して正確な時間を再現しています。

2.2 AcoustiXのベースエンジン: Sionna ray tracing

AcoustiXでは、音波の伝播経路を精密にシミュレーションするために、電波向けに開発された ray tracing シミュレータ Sionna ray tracing をベースエンジンとして使用しています。

Sionna ray tracingは、NVIDIAによって開発されたオープンソースの電波伝搬・通信系シミュレータです。次世代通信（6Gなど）のためのチャネルモデリングやエンドツーエンドの最適化を目的としており、以下のような特徴があります。

• GPUによる高速化：大規模・高精度なレイトレーシングを高速に実行可能
• TensorFlowを用いた微分可能なシミュレータ：送受信機の位置や向き、材質特性など、多くのパラメータに対する勾配を取得でき、最適化可能
  • 送信アンテナの向きを最適化して特定領域の受信電力を最大化
  • チャネル応答（CIR）とシミュレーション結果の誤差をもとに、反射面の材質パラメータ（導電率・誘電率）を推定
• 高精度な3Dシーン構築：Mitsuba 3 を用いて、3Dシーン内の構造・材質・ジオメトリなどを詳細かつ精緻に定義可能

2.3 AcoustiXによる拡張

AcoustiXでは、反射係数や拡散設定などの音響的パラメータを、電波シミュレータである Sionna ray tracing に適合するよう変換・調整してシミュレーションに使用しています。

Sionna ray tracing からは1本ずつのレイの情報（遅延時間、方向、複素振幅など）を受け取り、AcoustiX側で音響的な補正処理を行った上で、最終的にそれらを合成してIRを構成します。

具体的に行っている音響的な補正処理は以下の通りです。

• 遅延時間の考慮
  経路長に応じた遅延の反映

• 距離・反射に基づく減衰補正
  伝播距離や反射係数に応じたエネルギーのスケーリング

• 音源・マイクの指向性の考慮
  入射方向とデバイスの向きに応じたゲインの適用

このように、AcoustiXでは Sionna ray tracing をレイトレーシング用のシミュレータとして利用し、各レイに対して遅延や減衰といった音響特性を考慮して合成を行うことで、現実に即した高精度なIR生成を実現しています。

3. 実験と評価

3.1 実データセットでの生成IR精度

実環境で収録されたIRデータセットを用いてAVRを学習し、既存手法と比較して評価を行いました。使用した実データセットは以下の2種類です。各データセットのIRは0.1秒に切り詰め、90%を学習用、10%を評価用に用いました。

• MeshRIR：直方体空間におけるモノラルIRを収録。スピーカーは固定で、サンプリングレートは24kHz。
• Real Acoustic Fields (RAF)：オフィス環境（家具あり／なし）で収録されたモノラルIR。スピーカーは指向性あり、サンプリングレートは16kHz。

以下の指標でAVRと従来手法（NAF, INRAS, AAC, Opus）を比較しました。

• Phase：周波数領域における位相誤差
• Amp.：周波数領域における振幅誤差
• Env.：時間領域における包絡線誤差（%）
• T60：残響時間（ピークから60DB下がる時間）の誤差（%）
• C50：明瞭度（Clarity）の誤差（dB）
• EDT：Early Decay Time（ピークから10DB下がる時間） の誤差（ms）

AVRはほぼすべてのデータセット及び指標で従来手法を上回り、特に位相誤差において顕著な改善を示しました。
ランダムな位相を割り当てたときの位相誤差が1.62であることを考慮すると、AVRのみが位相情報を学習できていることがわかります。

---

3.2 シミュレーションデータセットでの生成IR精度

AcoustiXを用いて生成したシミュレーションデータでもAVRを学習し、同様に既存手法と比較して評価を行いました。シミュレーション環境として、以下の3つのシーンを用いました。

• 2D Room：中央に壁を1枚設けた、簡易的な長方形の空間
• 3D Room Avonia / Montreal：iGibsonデータセットに含まれる複雑な室内空間

各部屋には無指向性スピーカー1台を設置し、マイクはランダムに配置しました。IRは16kHzでサンプリングされ、長さは0.1秒に切り詰めました。データは90%を学習用、10%を評価用に使用しました。

AVRはほぼすべてのシーン及び指標で既存手法を上回りました。

3.3 音響場及び波形の可視化

音響場の可視化

以下の図は、MeshRIR及びシミュレーション環境における音響場の空間的な振幅・位相分布を可視化したものです。

従来手法（NAF, INRAS）は音源からの音声伝播パターンが捉えられておらず、空間全体での整合性が取れていません。
一方、AVRは空間全体で分布を正確に再現できています。

---

時間波形の可視化

以下は、モデルが予測した時間領域IRと正解のIRを比較した図です。

従来手法では、波形の全体的な減衰傾向は再現されているものの、ピークの位置などの詳細な形状をうまく捉えられていないことがわかります。
一方、AVRは正解に近い波形形状を再現できていることが確認できます。

3.4 ゼロショットのバイノーラル音響生成

AVRはモノラルな音響生成手法ですが、疑似的にバイノーラルの音響生成を行い、被験者によって音響の自然さを評価しました。
MeshRIRのシーンにおいて、リスナーから3メートル離れた位置に音源を設置し、左右の耳の位置（20cm間隔）でそれぞれインパルス応答生成する計算を行いました。リスナーが頭を左右に振る状況を想定し、AVR、NAF、INRASの各手法で生成されたバイノーラル音響を比較しました。

7名のユーザーに対して、音の聞こえ方と頭の動きの一致度を5段階で評価してもらった結果は以下のとおりです。

• AVR：4.71
• INRAS：1.86
• NAF：1.42

AVRは、インパルス応答の位相を正確に予測できるため、自然なバイノーラル音声を表現できたと考えられます。

4. 公式ソースコードで実験してみた

GitHub公式ソースコードを用いて、MeshRIRでAVRの学習及び推論を行いました。
ハイパーパラメータは論文記載の値を使用し、記載されていないパラメータについてはGitHubに記載されているデフォルト値を使用しました。
学習データ数は3572、テストデータ数は397です。
実験はシードを変えて5回行い、各指標計算時には平均と標準偏差を計算しました。

ABCI 3.0での実験手順

1. AVRリポジトリのクローン

git clone https://github.com/penn-waves-lab/AVR

2. 仮想環境と依存パッケージのインストール

ABCIのドキュメントを参考にvenvでPython仮想環境を作成し、AVRのREADMEに従って必要なパッケージをインストールします。

※ AVRのREADMEに記載してあるだけでは必要なパッケージが不足しており、最終的に以下のパッケージをインストールしました。

requirements.txt

torch
numpy
scipy
matplotlib
librosa
auraloss
pyyaml
tqdm
tensorboard
wheel

python -m venv ~/env
source ~/env/bin/activate
pip install -r requirements.txt

なお、tiny-cuda-nnはGPU環境でビルドする必要があるため、以下のようにインタラクティブジョブでGPUノードにログインしてインストールを行います。

# GPUノードにログイン
qsub -I -P grpname -q rt_HG -l select=1

# 仮想環境を有効化し、インストール
source ~/env/bin/activate
pip install git+https://github.com/NVlabs/tiny-cuda-nn/#subdirectory=bindings/torch

※ CUDA関連のビルドエラーが発生する場合は、CUDAバージョンを変更し、対応するようにPyTorchバージョンも調整してください。

3. MeshRIRデータセットの準備

AVRのREADMEに従い、MeshRIR S1-3969 datasetをダウンロード後、学習データとテストデータに分割します。

4. ハイパーパラメータの設定

AVR/config_files/avr_meshrir.yml を編集して、ハイパーパラメータ（例：合計ステップ数、各損失関数の重み、学習率など）を調整します。

5. バッチジョブスクリプトの作成と実行

ABCIのドキュメントを参考にして、以下のような学習用シェルスクリプト run_avr.sh を作成し、qsub run_avr.sh で学習ジョブを投入します。

run_avr.sh

#!/bin/bash
#PBS -q rt_HG
#PBS -l select=1
#PBS -l walltime=48:00:00
#PBS -P grpname
#PBS -N avr_meshrir
#PBS -o avr_meshrir_output.log
#PBS -e avr_meshrir_error.log

cd ~
source /etc/profile.d/modules.sh
module load cuda/11.8

source ~/env/bin/activate

python ~/AVR/avr_runner.py \
    --config ~/AVR/config_files/avr_meshrir.yml \
    --dataset_dir ~/MeshRIR

qsub run_avr.sh

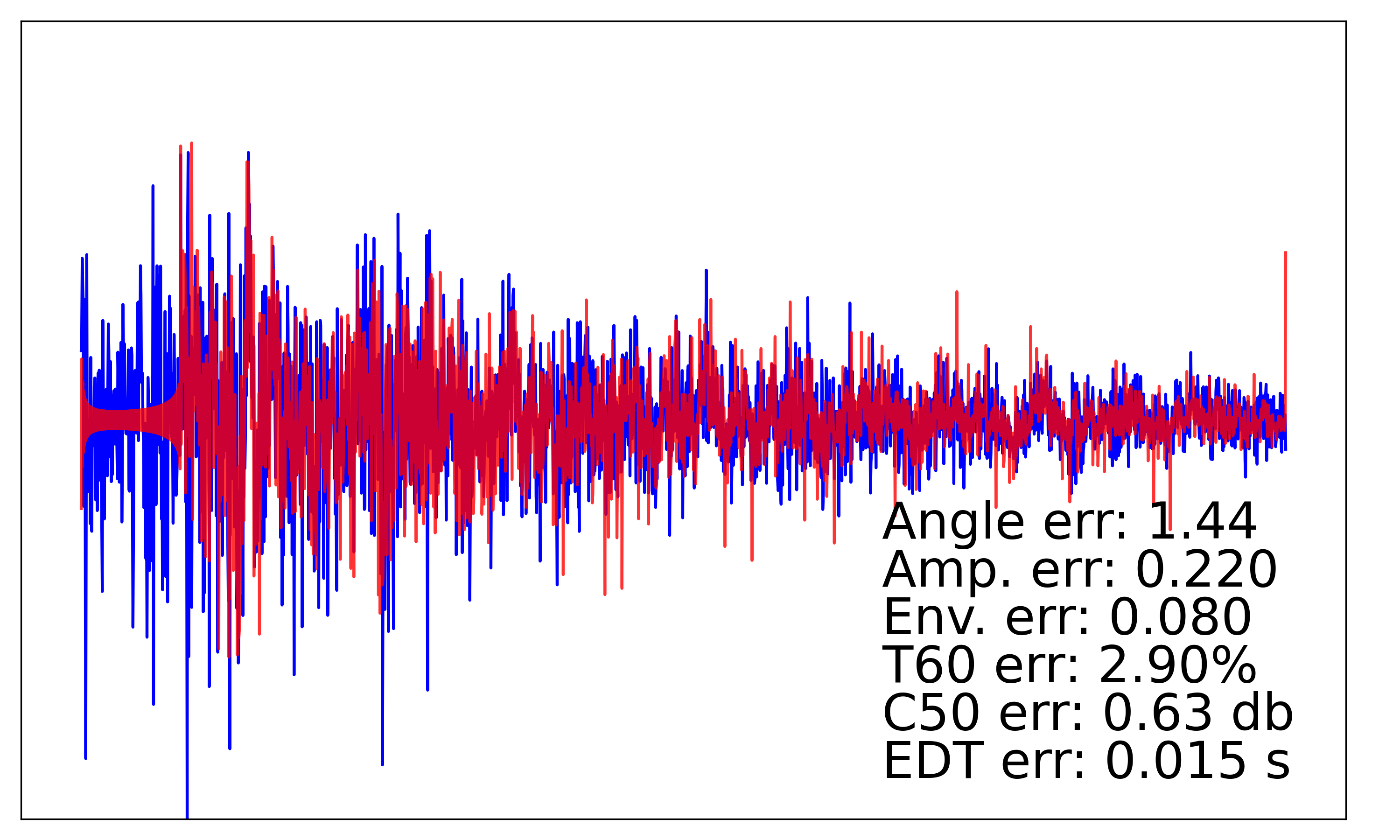
学習後にテストデータで生成波形を計算すると、以下のような図になりました。
青色が正解波形、赤色が生成波形を表しています。

また、各種指標での定量評価は、以下のようになりました。「実験結果(論文再現)」が今回の結果で、値が低い方が良い評価です。
振幅や残響時の誤差は論文で報告されている値より向上していますが、位相や包絡線の誤差は悪化していることがわかります。

比較対象	Phase	Amp.	Env. (%)	T60 (%)	C50 (dB)	EDT (ms)
論文値	0.85	0.54	1.15	3.9	0.92	35.1
実験結果 (論文再現)	1.44 ± 0.01	0.23 ± 0.00	7.95 ± 0.06	3.89 ± 1.37	0.54 ± 0.06	13.57 ± 1.54
実験結果 (GitHub)	1.29	0.15	7.67	2.9	0.38	8.6

これは、論文に未記載のハイパーパラメータが今回の実験と一致しないことによるものと考えられます。
試しに、全てのパラメータでGitHubに記載されているデフォルト値を使用した場合、上記の「実験結果(GitHub)」に記載した結果となりました。位相やEDTの誤差が大きく変わっていることがわかります。

これらの結果から、学習結果はハイパーパラメータの値に大きく影響されることがわかりました。
しかし、位相の学習がほとんできていなかったNAFと比較すると、AVRでは位相の学習が一定程度可能であると言えます。

おわりに

NeurIPS 2024 Spotlight に採択された「Acoustic Volume Rendering for Neural Impulse Response Fields」について、理論や手法、実験結果を整理しながら解説しました。

従来手法では難しかった 位相成分の学習 を、AVRは物理的な整合性を持つ構造によって可能にしています。加えて、モノラル音声のみで学習したにも関わらず、ゼロショットでのバイノーラル音響生成でも評価が高く、多チャンネル音響への応用も期待できます。

また、AVRと同時に提案されたAcoustiXを用いることで、特に位相成分について、IR生成における学習データの品質向上が期待できます。

(この記事は研究室インターンで取り組みました：https://kojima-r.github.io/kojima/)