「人流シミュレーションのパラメータ推定手法」の論文の実装(非公式)

はじめに

論文「人流シミュレーションのパラメータ推定手法」をPythonで実装しました。
実装したコードはgithubに載せています。
パッケージとして内容を実行することも可能です。
実装コードすべてを解説すると長くなるので、ここでは実装の概要とパッケージとしての利用法を解説します。(githubのREADME.mdにも同様の内容が書いてあります。)

• 追記(2021/2/17)
  Google Colaboratoryでの実行例(実装の概要の1～3番を実行)を公開しました。
  リンクはこちら

実装の概要

1. Social Force Model (SFM)を用いた人流モデルの実装
2. 全部のパラメータの最適化と目的関数の違いによる結果の評価
3. 個別のパラメータごとの最適化と目的関数の違いによる結果の評価
4. 2.の結果を踏まえた、全部のパラメータの最適化モデルの実装
5. 3.の結果を踏まえた、個別のパラメータごとの最適化モデルの実装

なお、4.と5.は基本的には実際の人流データに適用するものですが、この実装をした筆者自身は実際の人流データを用いたパラメータ推定は行っていません。(論文では行われています)

論文からの変更点

1. 人流シミュレーションにおいて遷移パラメータ(論文参照)を目的地ごとに決めるのではなく人ごとに正規分布で決定した。
2. パラメータ推定方法の評価において、ヒートマップの作り方はGridのみを用い、Voronoiは使わなかった。また、ヒートマップのGridの目の粗さに関しても評価せず、固定した。
3. パラメータ推定において、論文通りの推定法に加え、1種類のパラメータのみを推定して他のパラメータを固定する推定方法も実装した。(3. 個別のパラメータごとの最適化と目的関数の違いによる結果の評価と5.個別のパラメータごとの最適化モデルの実装に該当)

パッケージとしての利用

実行に必要なパッケージ

• numpy (version 1.19.2)
• matplotlib (version 3.3.2)
• optuna (version 2.4.0)

1. SFMを用いた人流モデル

1. 引数を指定

   people_num: シミュレーションする人数。

   v_arg: 人の速さに関連する2つの要素を持つリスト型の変数。1つ目の要素は平均の速さ、2つ目の要素は速さの標準偏差を表す。

   repul_h: 人の間の反発力に関連する2つの要素を持つリスト型の変数。
   (詳細:人流シミュレーションのパラメータ推定手法
   3.人流シミュレーションモデル 3.1 Social Force Model)

   repul_m: 人と壁の間の反発力に関連する2つの要素を持つリスト型の変数。
   (詳細:人流シミュレーションのパラメータ推定手法
   3.人流シミュレーションモデル 3.1 Social Force Model)

   target: 形が(N,2)のリスト型の変数。Nは目的地の数。2次元目の要素は目的地のxy座標を表す。最後の目的地は出口と見なされる。

   R: 人(粒子として表される)の半径

   min_p: 目的地にいる人が次の目的地に移動する確率の最小値。この確率の逆数が目的地での滞在時間の期待値として使われる。

   p_arg: 目的地にいる人が次の目的地に移動する確率を決定する2次元のリスト型の変数。1次元目の要素数は目的地の数から1を引いた数の因数。
   2次元目の1つ目の要素は確率の平均、2つ目の要素は標準偏差となる。この確率の逆数が目的地に滞在する時間の期待値として使われる。
   なお、1次元目の要素数が目的地の数から1引いた数より小さいとき、numpyのようにブロードキャストしてしようされる。

   wall_x: 壁のx座標(左端は0であり右端がこの変数により決定される)

   wall_y: 壁のy座標(下端は0であり上端がこの変数により決定される)

   in_target_d: 人と目的地の間の距離がこの変数より小さければ、その人は目的地に到着したと見なす。)

   dt: 人の状態(位置、速さなど)を更新するときに利用する微小時間の大きさ

   disrupt_point: 経過時間がこの変数を超えたらシミュレーションを停止する。(シミュレーション1/dt回で経過時間の1単位となる)

   save_format: シミュレーション結果を保存する形式を指定する。現在は"heat_map"だけしか使えない。"None"であれば結果を保存しない。

   save_params: 結果を保存するのに使う変数。"heat_map"であれば2つの要素を持ったリスト型の変数が必要で、1つ目の要素はヒートマップの行数と列数を指定するタプル、2つ目の要素は保存する頻度を指定する変数。頻度の単位は"disrupt_point"と同じ。

   people_num = 30
   v_arg = [6,2]
   repul_h = [5,5]
   repul_m = [2,2]
   target = [[60,240],[120,150],[90,60],[240,40],[200,120],[170,70],[150,0]]
   R = 3
   min_p = 0.1
   p_arg = [[0.5,0.1]]
   wall_x = 300
   wall_y = 300
   in_target_d = 3
   dt = 0.1
   save_format = "heat_map"
   save_params = [(30,30),1]
   

2. シミュレーションするインスタンスを生成

   import people_flow
   model = people_flow.simulation.people_flow(people_num,v_arg,repul_h,repul_m,target,R,min_p,p_arg,wall_x,wall_y,in_target_d,dt,save_format=save_format,save_params=save_params)
   

3. シミュレーションを実行(結果のヒートマップを得る)

   maps = model.simulate()
   

   実行中、シミュレーション状況がmatplotlibにより描画される。
   

2. 全部のパラメータの最適化と目的関数の違いによる結果の評価

SSD, SAD, KL, ZNCCの各目的関数を用いて全部のパラメータ最適化を行い、パラメータごとに最もよい結果となった目的関数を出力する。
(目的関数の詳細：人流シミュレーションのパラメータ推定手法 5.各処理の組み合わせの評価 5.1評価方法の全体像 表1)

1. 引数を指定

   maps: 3次元numpy.ndarray。パラメータ推定する人流データを表現するヒートマップ(各時刻においてGridの中にいる人数を表す)。
   people_num, target, R, min_p, wall_x, wall_y, in_target_d, dt, save_params: 人流シミュレーションに使う変数。1. SFMを用いた人流モデル参照

   v_range: (2,2)の形であるリスト型の変数。人の速さの平均と標準偏差を推定するとき、それぞれがとりうる値の範囲を表す。

   repul_h_range: (2,2)の形であるリスト型の変数。人の間の反発力に関する2つのパラメータを推定するとき、それぞれがとりうる値の範囲を表す。

   repul_m_range: (2,2)の形であるリスト型の変数。人と壁の間の反発力に関する2つのパラメータを推定するとき、それぞれがとりうる値の範囲を表す。

   p_range: (2,2)の形であるリスト型の変数。次の目的地に移動する確率の平均と標準偏差を推定するとき、それぞれがとりうる値の範囲を表す。
   なお、パラメータ推定では、次の目的地に移動する確率はどの目的地においても等しいものとして計算する。

   n_trials: 推定したパラメータを最適化する回数

   people_num = 30
   v_arg = [6,2]
   repul_h = [5,5]
   repul_m = [2,2]
   target = [[60,240],[120,150],[90,60],[240,40],[200,120],[170,70],[150,0]]
   R = 3
   min_p = 0.1
   p_arg = [[0.5,0.1]]
   wall_x = 300
   wall_y = 300
   in_target_d = 3
   dt = 0.1
   save_params = [(30,30),1]
   
   v_range = [[3,8],[0.5,3]]
   repul_h_range = [[2,8],[2,8]]
   repul_m_range = [[2,8],[2,8]]
   p_range = [[0.1,1],[0.01,0.5]]
   n_trials = 10
   

2. 評価するインスタンスを生成

   assessment = people_flow.assessment_framework.assess_framework(maps, people_num, v_arg, repul_h, repul_m, target, R, min_p, p_arg, wall_x, wall_y, in_target_d, dt, 
             save_params, v_range, repul_h_range, repul_m_range, p_range, n_trials)
   

3. すべての目的関数を用いてパラメータ推定を実行

   assessment.whole_opt()
   

4. 最高の目的関数の組み合わせを求める

   best_combination = assessment.assess()
   

5. パラメータ推定結果を正解と比較してグラフ化

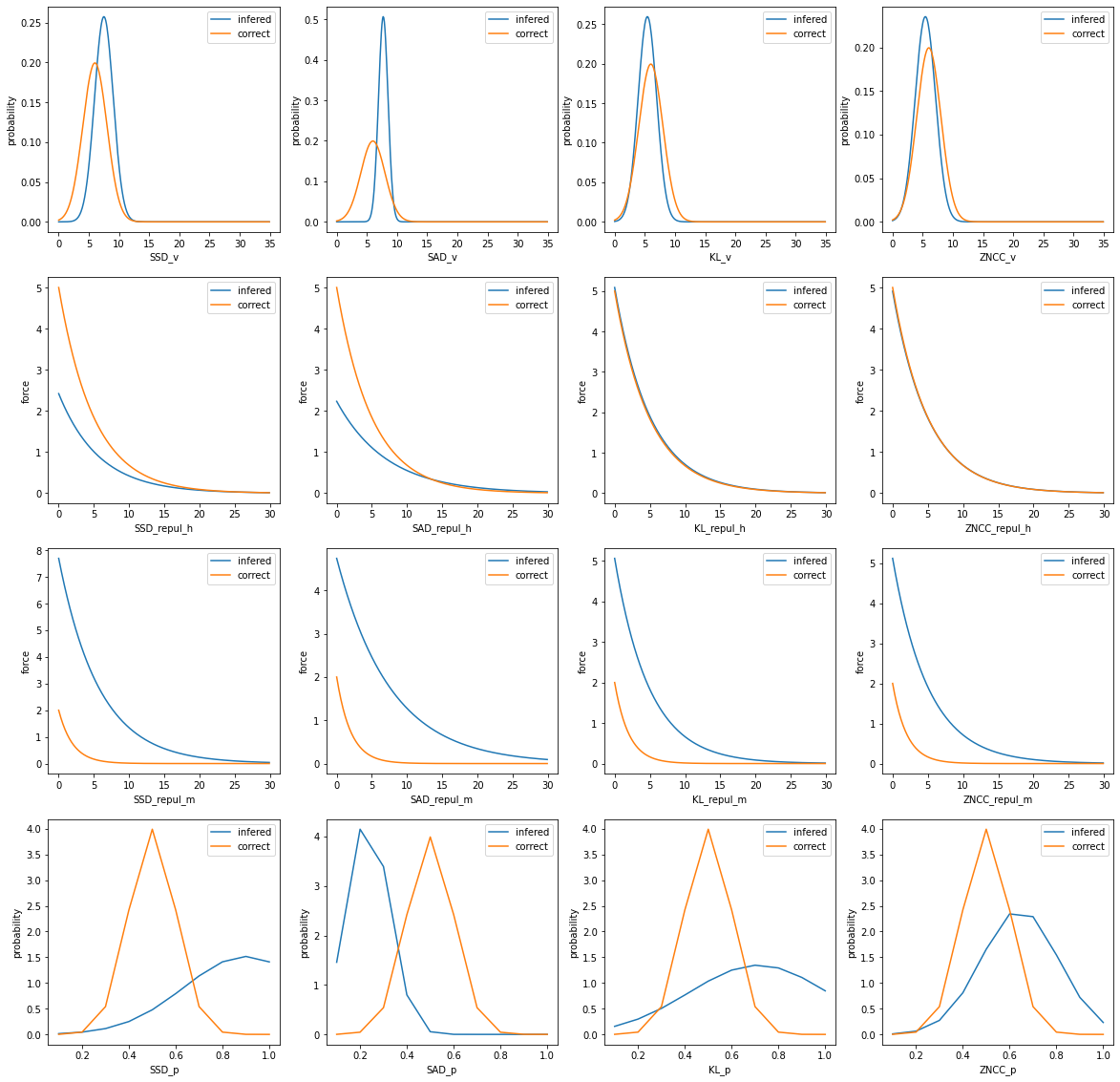
   assessment.assess_paint()
   

   1行目は人々の速さの正規分布をグラフ化したものであり、横軸は速さ、縦軸は確率密度を表す。
   2行目は人々の間の反発力の関数をグラフ化したものであり、横軸は人の間の距離、縦軸は力の大きさを表す。
   3行目は人と壁の間の反発力の関数をグラフ化したものであり、横軸は人と壁の間の距離、縦軸は力の大きさを表す。
   4行目は次の目的地に移動する確率をグラフ化したものであり、横軸は次の目的地に移動する確率、縦軸は確率密度を表す。
   また、各列は目的関数ごとの結果を表している。
   

3. 個別のパラメータごとの最適化と目的関数の違いによる結果の評価

SSD, SAD, KL, ZNCCの各目的関数を用いて個別のパラメータごとの最適化を行い、パラメータごとに最もよい結果となった目的関数を出力する。
(目的関数の詳細：人流シミュレーションのパラメータ推定手法 5.各処理の組み合わせの評価 5.1評価方法の全体像 表1)

1. 引数を指定

   maps: 3次元numpy.ndarray。パラメータ推定する人流データを表現するヒートマップ(各時刻においてGridの中にいる人数を表す)。
   people_num, target, R, min_p, wall_x, wall_y, in_target_d, dt, save_params: 人流シミュレーションに使う変数。1. SFMを用いた人流モデル参照

   v_range: (2,2)の形であるリスト型の変数。人の速さの平均と標準偏差を推定するとき、それぞれがとりうる値の範囲を表す。

   repul_h_range: (2,2)の形であるリスト型の変数。人の間の反発力に関する2つのパラメータを推定するとき、それぞれがとりうる値の範囲を表す。

   repul_m_range: (2,2)の形であるリスト型の変数。人と壁の間の反発力に関する2つのパラメータを推定するとき、それぞれがとりうる値の範囲を表す。

   p_range: (2,2)の形であるリスト型の変数。次の目的地に移動する確率の平均と標準偏差を推定するとき、それぞれがとりうる値の範囲を表す。
   なお、パラメータ推定では、次の目的地に移動する確率はどの目的地においても等しいものとして計算する。

   n_trials: 推定したパラメータを最適化する回数

   people_num = 30
   v_arg = [6,2]
   repul_h = [5,5]
   repul_m = [2,2]
   target = [[60,240],[120,150],[90,60],[240,40],[200,120],[170,70],[150,0]]
   R = 3
   min_p = 0.1
   p_arg = [[0.5,0.1]]
   wall_x = 300
   wall_y = 300
   in_target_d = 3
   dt = 0.1
   save_params = [(30,30),1]
   
   v_range = [[3,8],[0.5,3]]
   repul_h_range = [[2,8],[2,8]]
   repul_m_range = [[2,8],[2,8]]
   p_range = [[0.1,1],[0.01,0.5]]
   n_trials = 10
   

2. 評価するインスタンスを生成

   assessment_detail = people_flow.assessment_framework.assess_framework_detail(maps, people_num, v_arg, repul_h, repul_m, target, R, min_p, p_arg, wall_x, wall_y, in_target_d, dt, 
             save_params, v_range, repul_h_range, repul_m_range, p_range, n_trials)
   

3. すべての目的関数を用いてパラメータ推定を実行

   assessment_detail.whole_opt()
   

4. 最高の目的関数の組み合わせを求める

   best_combination = assessment_detail.assess()
   

5. パラメータ推定結果を正解と比較してグラフ化

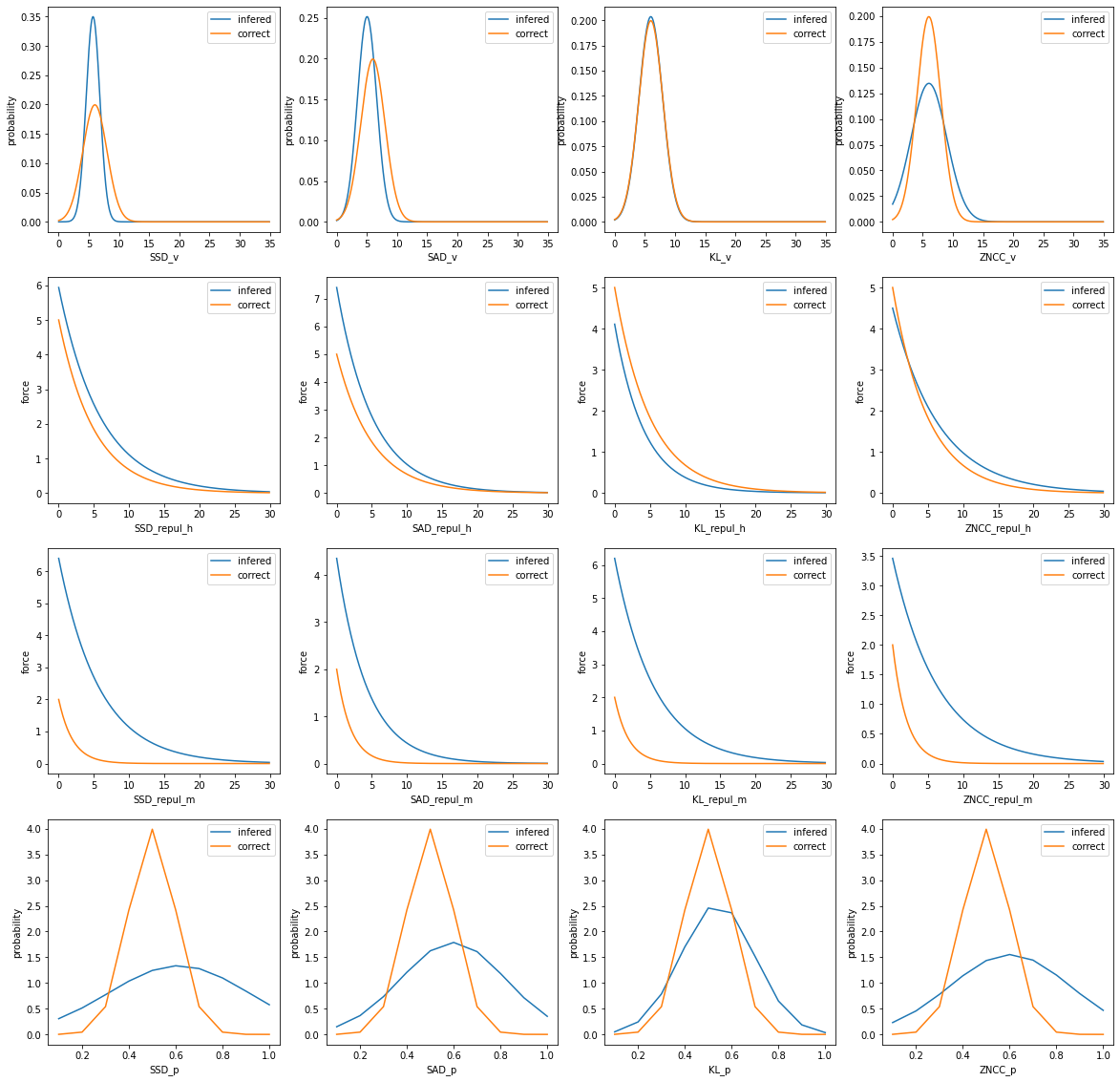
   assessment_detail.assess_paint()
   

   1行目は人々の速さの正規分布をグラフ化したものであり、横軸は速さ、縦軸は確率密度を表す。
   2行目は人々の間の反発力の関数をグラフ化したものであり、横軸は人の間の距離、縦軸は力の大きさを表す。
   3行目は人と壁の間の反発力の関数をグラフ化したものであり、横軸は人と壁の間の距離、縦軸は力の大きさを表す。
   4行目は次の目的地に移動する確率をグラフ化したものであり、横軸は次の目的地に移動する確率、縦軸は確率密度を表す。
   また、各列は目的関数ごとの結果を表している。
   

4. 全部のパラメータの最適化モデルの実装

SSD, SAD, KL, ZNCCの各目的関数を用いて全部のパラメータ最適化を行い、2. 全部のパラメータの最適化と目的関数の違いによる結果の評価の結果を踏まえて、パラメータごとに最適な目的関数を使った最適化結果を選び、出力する。

1. 引数を指定
   1. SFMを用いた人流モデル、2. 全部のパラメータの最適化と目的関数の違いによる結果の評価を参照

   people_num = 30
   target = [[60,240],[120,150],[90,60],[240,40],[200,120],[170,70],[150,0]]
   R = 3
   min_p = 0.1
   wall_x = 300
   wall_y = 300
   in_target_d = 3
   dt = 0.1
   save_params = [(30,30),1]
   
   v_range = [[3,8],[0.5,3]]
   repul_h_range = [[2,8],[2,8]]
   repul_m_range = [[2,8],[2,8]]
   p_range = [[0.1,1],[0.01,0.5]]
   n_trials = 10
   

2. 推定するインスタンスを生成

   inference = people_flow.inference_framework.inference_framework(maps, people_num, target, R, min_p, wall_x, wall_y, in_target_d, dt, save_params, v_range, repul_h_range, repul_m_range, p_range, n_trials)
   

3. パラメータ推定を実行(推定したパラメータを得る)

   inferred_params = inference.whole_opt()
   

5. 個別のパラメータごとの最適化モデルの実装

SSD, SAD, KL, ZNCCの各目的関数を用いて個別のパラメータごとの最適化を行い、3. 個別のパラメータごとの最適化と目的関数の違いによる結果の評価の結果を踏まえて、パラメータごとに最適な目的関数を使った最適化結果を選び、出力する。

1. 引数を指定
   1. SFMを用いた人流モデル、3. 個別のパラメータごとの最適化と目的関数の違いによる結果の評価を参照

   people_num = 30
   v_arg = [6,2]
   repul_h = [5,5]
   repul_m = [2,2]
   target = [[60,240],[120,150],[90,60],[240,40],[200,120],[170,70],[150,0]]
   R = 3
   min_p = 0.1
   p_arg = [[0.5,0.1]]
   wall_x = 300
   wall_y = 300
   in_target_d = 3
   dt = 0.1
   save_params = [(30,30),1]
   
   v_range = [[3,8],[0.5,3]]
   repul_h_range = [[2,8],[2,8]]
   repul_m_range = [[2,8],[2,8]]
   p_range = [[0.1,1],[0.01,0.5]]
   n_trials = 10
   

2. 推定するインスタンスを生成

   inference_detail = people_flow.inference_framework.inference_framework_detail(maps, people_num, v_arg, repul_h, repul_m, target, R, min_p, p_arg, wall_x, wall_y, in_target_d, dt, save_params, v_range, repul_h_range, repul_m_range, p_range, n_trials)
   

3. パラメータ推定を実行(推定したパラメータを得る)

   inferred_params_detail = inference_detail.whole_opt()
   

おわりに

論文「人流シミュレーションのパラメータ推定手法」のPythonによる実装の概要とgithubに載せた実装コードのパッケージとしての利用法を説明しました。
不明な点、実装コードに関するアドバイス、パッケージとして利用する際の問題などありましたらコメントお願いします。

(この記事は研究室インターンで取り組みました：https://kojima-r.github.io/kojima/)