はじめに
この記事はSIGNATEの 【第32回_Beginner限定コンペ】診断データを使った糖尿病発症予測 に挑戦した際の解放を示した備忘録です。
このコンペで規定のスコアをクリアすれば Intermediate の称号を獲得することができます。
私はバックグラウンドとして病院や薬局で薬剤師として勤務していた経験があるので(現在は半引退状態)、糖尿病の発症予測 という 医療系の内容 を扱うのが自分のステップアップに相応しいと思い、このコンペを選びました。
モデルは LightGBM、ハイパーパラメータ探索にOptuna の LightGBMTunerを使用しています。
ここをクリアし、まずは完全初心者という立場からの脱却を目指します。
目次
1. 実行環境
2. データの確認
3. 異常値・外れ値の処理
4. 簡易学習モデルの作成、精度の確認
5. 特徴量エンジニアリング
6. ハイパーパラメータチューニング
7. テストデータの予測、提出
8. Focal Lossの試用
9. 感想
10. 参考文献
1. 実行環境
- Python 3.9.13
- Docker Desktop for Mac (version 4.17.0)
- MacBook Pro (16-inch, 2019)(11.2.3)
- macOS Ventura 13.3
2. データの確認
データの持っている特徴量は以下の通りです。
| 特徴量 | 内容 |
|---|---|
| index | インデックス |
| Pregnancies | 妊娠回数 |
| Glucose | 血中グルコース濃度(血糖値) |
| BloodPressure | 血圧(ここでは拡張期血圧) |
| SkinThickness | 皮膚のひだの厚さ |
| Insulin | 血清インスリン値 |
| BMI | 肥満度を表す指数 |
| DiabetesPedigreeFunction | 糖尿病の遺伝的リスクのスコア |
| Age | 年齢 |
| Outcome | 0 or 1 (1だと糖尿病) |
まずは学習データの中身を確認してみます。
# trainデータの読み込み
train_df = pd.read_csv('../data/train.csv')
train_df.head(3)
欠損値があるかどうかも見てみます。
# trainデータの欠損値を確認
train_df.isna().any()
index False
Pregnancies False
Glucose False
BloodPressure False
SkinThickness False
Insulin False
BMI False
DiabetesPedigreeFunction False
Age False
Outcome False
dtype: bool
続いてテストデータの中身を確認してみます。
# testデータの読み込み
test_df = pd.read_csv('../data/test.csv')
test_df.head(3)
テストデータの方も欠損値があるかどうか見てみます。
# testデータの欠損値を確認
test_df.isna().any()
index False
Pregnancies False
Glucose False
BloodPressure False
SkinThickness False
Insulin False
BMI False
DiabetesPedigreeFunction False
Age False
dtype: bool
どちらのデータセットにも欠損値はないようです。
Beginners限定コンペだからでしょうか。
これからの処理を楽にするために、学習データとテストデータを結合します。
データを区別するために"separate"というカラムを一時的に追加しておきます。
# trainデータとtestデータの結合
train_df['separate'] = 'train'
test_df['separate'] = 'test'
df = pd.concat([train_df, test_df])
ここで今回のデータの統計量を確認したところ、おかしなものに気付きました。
# 統計量を確認
df.describe()
血圧の最低値が0になっています。
被験者の中に人知を超えた究極生物でもいたとしたら別ですが、通常はありえません。
そしてBMIの最低値が0.000775になっています。
BMIは
BMI = \frac{体重(kg)}{身長(m)^2}
で表されるため、体重ほぼ0 か 身長ほぼ無限 みたいな、我々が知っている人類の範疇を逸脱した人間でもない限りありえません。
そもそもそんな奴がいたとしたら、糖尿病云々の前にモンスターボールを投げつけて捕獲すると思います。
それぞれの特徴量をざっと可視化してみます。
おそらく後でまた使うコードになると思うので、関数化しておきます。
def plot_features(data, num=4, figsize=(30, 15)):
"""
Plot histogram for each feature in the given DataFrame.
Args:
data: A pandas DataFrame containing the data to plot.
num: An int representing the number of subplots to display in each row.
Default is 4.
figsize: A tuple representing the size of the figure.
Default is (30, 15).
Returns:
None
"""
columns = data.drop(columns=['index', 'Outcome', 'separate']).columns
fig, axes = plt.subplots(int(len(columns) / num), num, figsize=figsize)
for i, column in enumerate(columns):
sns.histplot(data[column], ax=axes[i // num, i % num])
return
# 可視化
plot_features(df)
分布に結構偏りがありますね。
とりあえず、まずは先程の異常値に対応する必要がありそうです。
3. 異常値・外れ値の処理
先程出てきた血圧とBMIの異常値、それと外れ値の対応を考えてみます。
◇ BMI
まずはBMIについてです。
改めてデータを可視化してみます。
sns.displot(df['BMI'], height=4)
BMIが0付近のデータに特徴があるかどうか調べてみます。
見た感じ、BMIが20付近からはデータがほとんどなさそうに見えるので、20以下のデータについて確認してみます。
# BMIが20以下のデータの統計を調べる
bmi_outlier = df[df['BMI'] <= 20]
bmi_outlier['BMI'].describe()
count 51.000000
mean 0.001303
std 0.000229
min 0.000775
25% 0.001158
50% 0.001272
75% 0.001492
max 0.001806
Name: BMI, dtype: float64
BMIが20以下のデータはすべてBMIが約0と考えてよさそうです。
各特徴量の分布を可視化してみます。
# BMIが20以下のデータの各特徴量のデータ分布を可視化
plot_features(bmi_outlier)
可視化したグラフを見る限り、データ全体の分布と比べて特に大きな特徴があるようには思えないので、異常値には BMIの中央値 を代入することで対応することにします。
# BMI <= 20 のデータの 'BMI' に中央値を代入する
bmi_median = df['BMI'].median()
df['BMI'] = df['BMI'].apply(lambda x: bmi_median if x <= 20 else x)
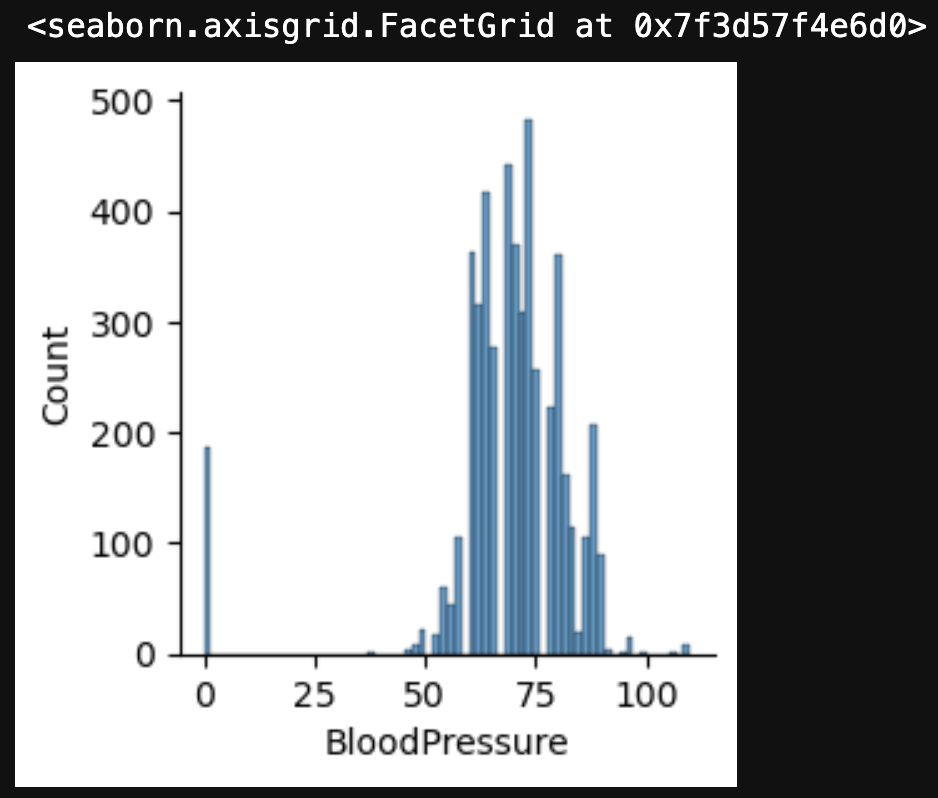
◇ BloodPressure
次にBloodPressureについてです。
改めてデータを可視化してみます。
sns.displot(df['BloodPressure'], height=4)
BloodPressureが0付近のデータに特徴があるかどうか調べてみます。
見た感じ、25付近からはデータがほとんどなさそうに見えるので、25未満のデータについて確認してみます。
# BloodPressureが25未満のデータの統計を調べる
dbp_outlier = df[df['BloodPressure'] < 25]
dbp_outlier['BloodPressure'].describe()
count 186.0
mean 0.0
std 0.0
min 0.0
25% 0.0
50% 0.0
75% 0.0
max 0.0
Name: BloodPressure, dtype: float64
血圧が25未満のデータは186件あり、すべて血圧0ということがわかりました。
究極生物やらゾンビやらが186体いるのでしょうか。
各特徴量の分布を可視化してみます。
# BloodPressureが25未満のデータの各特徴量のデータ分布を可視化
plot_features(dbp_outlier)
可視化したグラフを見る限り、データ全体の分布と比べて特に大きな特徴があるようには思えないので、異常値には BloodPressureの中央値 を代入することで対応することにします。
# BloodPressure == 0 のデータの 'BloodPressure' に中央値を代入する
dbp_med = int(df['BloodPressure'].median())
df['BloodPressure'] = df['BloodPressure'].apply(lambda x: dbp_med if x == 0 else x)
次に外れ値について考えていきます。
データの 両側1% を 外れ値 として除外するパターンと 両側5% を除外するパターンをそれぞれ作成し、後ほど簡易的な学習器を作成して現時点での精度を確認してみることにします。
# 外れ値をクリッピングする関数
def clipping_outlier(data, exclusion_col, clip_range):
"""
Clip outliers by clipping both sides of the distribution.
Args:
data: A pandas DataFrame containing the data.
exclusion_col: A list of features to exclude from outlier clipping.
clip_range: A float indicating the percentage to exclude on each side of the distribution.
Returns:
A pandas DataFrame with outliers removed.
"""
data_copy = data.copy()
columns = data_copy.drop(columns=exclusion_col).columns
for column in columns:
outliers = list(data_copy[column].quantile([clip_range, 1 - clip_range]))
data_copy[column] = np.clip(data_copy[column], outliers[0], outliers[1])
return data_copy
# 外れ値の処理
exclusion_col = ['index', 'Outcome', 'separate']
df_1 = clipping_outlier(df, exclusion_col, 1)
df_5 = clipping_outlier(df, exclusion_col, 5)
# データの保存
df_1.to_csv('df_1.csv', index=False)
df_5.to_csv('df_5.csv', index=False)
右に裾を引いている特徴量 がいくつかありますが、端っこの 1~5% をクリッピングする分にはほとんど影響がなさそうなので、このままいきます。
4. 簡易学習モデルの作成、精度の確認
現時点でどの程度スコアを出せるか確認するために 簡易的な学習モデル を作成します。
モデルは LihgtGBM を使用し、ハイパーパラメータは学習率だけ 0.01 に変更します。
# 精度確認のための簡易学習器を定義
def simple_classifier(X, y):
"""
A simplified binary classification model to check accuracy using LightGBM.
Args:
X (pandas.DataFrame): Feature dataset.
y (pandas.Series): Binary labels.
Returns:
tuple (float, float, lightgbm.Booster): Mean accuracy score, mean AUC score, trained LightGBM model.
"""
accuracies = []
auc_scores = []
params = {'objective': 'binary',
'metric': 'binary_logloss',
'boosting_type': 'gbdt',
'verbose': -1,
'random_state': 0,
'learning_rate': 0.01,
}
callbacks = []
callbacks.append(lgb.early_stopping(stopping_rounds=10, verbose=False))
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=10)
for train_index, val_index in cv.split(X, y):
X_train, X_val = X.iloc[train_index], X.iloc[val_index]
y_train, y_val = y[train_index], y[val_index]
train_data = lgb.Dataset(X_train, y_train)
val_data = lgb.Dataset(X_val, y_val)
valid_sets = [val_data]
model = lgb.train(params,
train_data,
num_boost_round=1000,
valid_sets=valid_sets,
callbacks=callbacks,
)
y_pred = model.predict(X_val)
y_pred = np.rint(y_pred)
accuracy = accuracy_score(y_val, y_pred)
accuracies.append(accuracy)
auc = roc_auc_score(y_val, y_pred)
auc_scores.append(auc)
return np.mean(accuracies), np.mean(auc_scores), model
スコアを見てみます。
# 両側1%をクリッピングしたデータの読み込み
df_1 = pd.read_csv('df_1.csv')
train1 = df_1[df_1['separate'] == 'train']
# 'index' と 'separate' は不要なので落とす
train1 = train1.drop(columns=['index', 'separate'])
# データの振り分け、スコアの確認
X1 = train1.loc[:, train1.columns!='Outcome']
y1 = train1['Outcome']
accuracy, auc, model_1 = simple_classifier(X1, y1)
print(f'Accuracy: {accuracy}, AUC: {auc}')
Accuracy: 0.8030000000000002, AUC: 0.6581958173725132
# 両側5%をクリッピングしたデータの読み込み
df_5 = pd.read_csv('df_5.csv')
train5 = df_5[df_5['separate'] == 'train']
# 'index' と 'separate' は不要なので落とす
train5 = train5.drop(columns=['index', 'separate'])
# データの振り分け、スコアの確認
X5 = train5.loc[:, train5.columns!='Outcome']
y5 = train5['Outcome']
accuracy, auc, model_5 = simple_classifier(X5, y5)
print(f'Accuracy: {accuracy}, AUC: {auc}')
Accuracy: 0.8089999999999999, AUC: 0.6645053653590449
わずかな差ではありますが、両側5%をクリッピングしたデータの方がスコアが高いので、このデータをベースに進めていきます。
ここで変数名を変えておきます。
# 変数名を変更
X = X5
y = y5
model = model_5
5. 特徴量エンジニアリング
特徴量エンジニアリングについて考えていきます。
正直これについては経験が浅過ぎるので、意味のあることができるかどうか微妙なところです。
とりあえず現時点で簡単に思いつくものをいくつか試してみたいと思います。
簡易学習器を使用した際の特徴量の重要度を見てみます。
# 特徴量の重要度を可視化
lgb.plot_importance(model)
'BMI' と 'DiabetesPedigreeFunction' 、それから 'Glucose' が上位にきています。
糖尿病は遺伝性があるので遺伝的リスクのスコアは重要でしょうし、BMIと血糖値も臨床上重要なパラメータです。
まずは 'BMI' と 'Glucose' が 臨床上の異常値であるか否か のラベルを作り、それが精度向上に寄与するかどうかを見てみます。
この 'Glucose' という特徴量は ブドウ糖負荷試験2時間値 で、 正常型 となるのは 140mg/dL未満 なので、この値を境に 正常型 と そうでない かを区別するラベルを作ってみます。
# ブドウ糖負荷試験2時間値が正常型かそうでないかのラベル
X['OGTT_anomaly'] = X['Glucose'].apply(lambda x: 0 if x < 140 else 1)
accuracy, auc, _ = simple_classifier(X, y)
print(f'Accuracy: {accuracy}, AUC: {auc}')
Accuracy: 0.8109999999999999, AUC: 0.667259722599179
元が0.808ぐらいなので、少し精度が上がりました。
とりあえずこの特徴量はキープです。
次にBMIを使ってみます。
今作った 'OGTT_anomary' はいったんリセットします。
アメリカ疾病予防管理センターの基準では、25 < BMI < 30 で やや肥満、BMI >= 30 で 肥満 と区分しています。
しかしBMIを両側5%でクリッピングしているので ほとんどが30以上 となり、この基準では意味がなさそうです。
X['BMI'].describe()
count 3000.000000
mean 35.625556
std 6.413437
min 26.880075
25% 32.599471
50% 33.835873
75% 39.578256
max 51.038429
Name: BMI, dtype: float64
そこで、BMI全体の平均値との比率を特徴量にしてみたいと思います。
# BMIの平均値との比率
bmi_mean = np.mean(X['BMI'])
X['bmi_diff'] = X['BMI'] / bmi_mean
accuracy, auc, _ = simple_classifier(X, y)
print(f'Accuracy: {accuracy}, AUC: {auc}')
Accuracy: 0.8089999999999999, AUC: 0.6645053653590449
元の精度と差がないので、これは意味がなさそうです。
他にも以下のような特徴量を作成して精度を見てみましたが、変わらないかごく僅かに精度が変動するという結果でした。
- 世代ごとに遺伝的リスクのスコアの平均値を算出し、差を特徴量とする
- 拡張期血圧で高血圧の重症度分類を示した特徴量
- Insulin / Glucose
- 妊娠回数が7以上かそうでないか
- 世代別に妊娠数の中央値を計算し、差を特徴量とする
- BMI, Glucose, BloodPressureをそれぞれ標準化し、掛け合わせてみる
これ以上模索するよりも、ハイパーパラメータチューニングをしてみたいと思います。
特徴量エンジニアリングに限った話ではありませんが、本当に未熟さを痛感します。
6. ハイパーパラメータチューニング
Optuna の LightGBMTuner を使ってハイパーパラメータのチューニングを行います。
LightGBMTuner は複数のハイパーパラメータを同時に自動調整し、相互作用の影響を考慮した最適化が可能なので便利です。
import optuna.integration.lightgbm as lgb
from sklearn.model_selection import train_test_split
# データを分割
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.3, random_state=10)
# LightGBM用データセットに変換
train_data = lgb.Dataset(X_train, y_train)
val_data = lgb.Dataset(X_val, y_val)
# 最小限のパラメータを定義
params = {'objective': 'binary',
'metric': 'binary_logloss',
'verbose': -1,
'boosting_type': 'gbdt',
}
callbacks = []
callbacks.append(lgb.early_stopping(stopping_rounds=10, verbose=False))
# LightGBMTunerを定義
tuner = lgb.LightGBMTuner(params=params,
train_set=train_data,
valid_sets=val_data,
callbacks=callbacks,
optuna_seed=100,
)
# チューニングを実行
tuner.run()
# ベストモデルを取得
best_model = tuner.get_best_booster()
# 正解率とAUCを確認
y_pred = best_model.predict(X_val)
y_pred = np.rint(y_pred)
accuracy = accuracy_score(y_val, y_pred)
auc = roc_auc_score(y_val, y_pred)
print(f'Accuracy: {accuracy}')
print(f'AUC: {auc}')
Accuracy: 0.8288888888888889
AUC: 0.7045839851804335
このモデルでテストデータを予測し、提出してみようと思います。
ちなみにベストパラメータはこんな感じです。
# ベストパラメータの取得
tuner.best_params
{'objective': 'binary',
'metric': 'binary_logloss',
'verbose': -1,
'boosting_type': 'gbdt',
'feature_pre_filter': False,
'lambda_l1': 0.2019055894080857,
'lambda_l2': 3.5275169933928286e-07,
'num_leaves': 31,
'feature_fraction': 0.7,
'bagging_fraction': 1.0,
'bagging_freq': 0,
'min_child_samples': 20}
7. テストデータの予測と提出
両側5%をクリッピングして保存したデータからテストデータを切り出し、少し精度が向上した特徴量の 'OGTT_anomaly' を追加します。
# テストデータの切り出し
test_df = df_5[df_5['separate'] == 'test']
# 特徴量 'OGTT_anomaly' を追加
test_df['OGTT_anomaly'] = test_df['Glucose'].apply(lambda x: 0 if x < 140 else 1)
# 不要なカラムを落とす
test_df = test_df.drop(columns=['Outcome', 'separate'])
先程のベストモデルを使って予測します。
# テストデータをインデックスとそれ以外に分離
idx = test_df['index']
X_test = test_df.drop(columns='index')
# 予測
preds = best_model.predict(X_test)
y_pred = pd.Series(np.rint(preds))
# データの確認
y_pred
0 0
1 0
2 0
3 0
4 0
..
1995 0
1996 0
1997 1
1998 0
1999 0
Length: 2000, dtype: int64
# 予測値とインデックスを結合
submission = pd.concat([idx, y_pred], axis=1)
# データの保存
submission.to_csv('../submissions/submission_5.csv', header=False, index=False)
指定されたフォーマットのcsvファイルを提出し、結果を通達するメールが届きました。

称号獲得のボーダーとなるAccuracyが 0.7960000 だったのでギリギリでしたが、目標である Intermediate の称号を獲得できました。
ちなみに最終順位は64位で少々不甲斐ないのですが、ここでは称号を獲得することが目的だったので、これでよしとしておきます。
8. Focal Lossの試用
前々から損失関数の Focal Loss というものが気になっていたので、この機会に少し試してみたいと思います。
元々は物体検出モデルの学習時に発生する 不均衡問題 を解決するための損失関数だそうで、多くの不均衡な学習問題にも使用されているとか。
今回の学習データのラベルの比率はこんな感じです。
np.unique(y_train, return_counts=True)
(array([0., 1.]), array([1826, 574]))
sns.countplot(y_train)
不均衡と言えば不均衡です。
試しに ChatGPT に聞いてみたら、こんな回答でした。
今回のデータでは 3:1 ぐらいですが、物は試しということでやってみたいと思います。
Focal Lossを実装するにあたり、LightGBMの公式ドキュメントやFocal Lossに関する記事を参考にしましたが、ポイントは以下の通りでした。
- LightGBMの
train関数の引数であるfobjに自分で定義したカスタム関数を渡す。 - カスタム損失関数の引数と戻り値に指定があり、特に戻り値はカスタム関数の
一階微分と二階微分を返す必要がある。 - LightGBMが返す
preds配列は確率ではないため、自分で確率に変換する必要がある。 -
評価関数でも同じことが起こるため、train関数のfevalにそれに対応した評価関数を渡す必要がある。 - カスタム損失関数を使用する場合、
初期化値を指定する必要がある。- 各Datasetの
init_scoreパラメータに初期化値を設定 - 学習後のテストデータの予測をする際、
シグモイド変換前に初期化値を追加する。
- 各Datasetの
これらのポイントに気を付けつつ、実装していきたいと思います。
まず、Focal Lossは以下の式で表されます。
αtとptはそれぞれ以下のように表されます。
yはいわゆる正解ラベル(y_true)で0か1で表されるため、boolian型 と見做せます。
なので、以下のように表現することができます。
# pt
pred_t = np.where(y_true, y_pred, 1 - y_pred)
# αt
alpha_t = np.where(y_true, alpha, 1 - alpha)
# Focal Loss
focal_loss = -alpha_t * (1 - pred_t)**gamma * np.log(pred_t)
Focal Lossの 一階微分 と 二階微分 を定義します。
参考にした記事に式の展開があったので、最終形を利用させてもらいます。
一般的に 予測値y は 0 or 1 の値をとりますが、Focal Lossの論文の中で著者は y を -1 or 1 であると仮定しており、この一階微分と二階微分の式はそれが前提になっているようです。
なので、y の値を y∈{0, 1} から y∈{-1, 1} に変換する必要があります。
一階微分と二階微分はそれぞれ以下の式で表されます。
これらの式は結果的に以下のように表現されます。
# y∈{0, 1} から y∈{-1, 1} に変換
y_true = 2 * y_true - 1
# 一階微分
gradient = alpha_t * y_true * (1 - pred_t)**gamma * (gamma * pred_t * np.log(pred_t) + pred_t - 1)
# 二階微分
du_dpt = -gamma * alpha_t * y_true * (1 - pred_t)**(gamma - 1)
v = gamma * pred_t * np.log(pred_t) + pred_t - 1
u = alpha_t * y_true * (1 - pred_t)**gamma
dv_dpt = gamma * np.log(pred_t) + gamma + 1
dpt_dp = y_true
dp_dz = y_pred * (1 - y_pred)
hessian = (du_dpt*v + dv_dpt*u) * dpt_dp * dp_dz
train関数の fobj に渡すカスタム損失関数と feval に渡すカスタム評価関数を定義します。
公式ドキュメントによると、fobj の引数と戻り値は以下のように指定されています。
また、feval の引数と戻り値は以下のように指定されています。
これらを満たすように関数を定義します。
一階微分と二階微分が必要になりますが、このルールでは引数で渡すことができません。
先程のものを関数化し、カスタム関数の中で使う必要がありそうです。
そして薄々勘付いていましたが、いろいろな箇所で γ や α といったパラメータが登場したり、これから定義しようとしていた 初期化値 も含めて関連した変数を何回も使うことになるので、これは クラス化 した方がよさそうです。
参考にした記事でもクラスを定義していました。
というわけで、Focal Lossをクラス化したものが以下のコードです。
初期化値については参考記事と同様、optimizeモジュール を使用しました。
(見づらくなりそうなので、今回はdocstringを省略しました)
class Focal_Loss:
def __init__(self, gamma, alpha=None):
self.alpha = alpha
self.gamma = gamma
def _pred_t(self, y_true, y_pred):
pred_t = np.where(y_true, y_pred, 1 - y_pred)
return pred_t
def _alpha_t(self, y_true):
alpha_t = np.where(y_true, self.alpha, 1 - self.alpha)
return alpha_t
def _focal_loss(self, y_true, y_pred):
alpha_t = self._alpha_t(y_true)
pred_t = self._pred_t(y_true, y_pred)
loss = -alpha_t * (1 - pred_t)**self.gamma * np.log(pred_t)
return loss
def _gradient(self, y_true, y_pred):
# y∈{0, 1} から y∈{-1, 1} に変換
y_true2 = 2 * y_true - 1
alpha_t = self._alpha_t(y_true)
pred_t = self._pred_t(y_true, y_pred)
grad = alpha_t * y_true2 * (1 - pred_t)**self.gamma * (self.gamma * pred_t * np.log(pred_t) + pred_t - 1)
return grad
def _hessian(self, y_true, y_pred):
# y∈{0, 1} から y∈{-1, 1} に変換
y_true2 = 2 * y_true - 1
alpha_t = self._alpha_t(y_true)
pred_t = self._pred_t(y_true, y_pred)
du_dpt = -self.gamma * alpha_t * y_true2 * (1 - pred_t)**(self.gamma - 1)
v = self.gamma * pred_t * np.log(pred_t) + pred_t - 1
u = alpha_t * y_true2 * (1 - pred_t)**self.gamma
dv_dpt = self.gamma * np.log(pred_t) + self.gamma + 1
dpt_dp = y_true2
dp_dz = y_pred * (1 - y_pred)
hess = (du_dpt*v + dv_dpt*u) * dpt_dp * dp_dz
return hess
def lgb_fobj(self, preds, train_data):
# 学習データからラベルを取得
y_true = train_data.get_label()
# シグモイド関数で確率変換
y_pred = special.expit(preds)
grad = self._gradient(y_true, y_pred)
hess = self._hessian(y_true, y_pred)
return grad, hess
def lgb_feval(self, preds, train_data):
# 学習データからラベルを取得
y_true = train_data.get_label()
# シグモイド関数で確率変換
y_pred = special.expit(preds)
is_higher_better = False
return 'focal_loss', self._focal_loss(y_true, y_pred).mean(), is_higher_better
def init_score(self, y_true):
res = optimize.minimize_scalar(lambda x: self._focal_loss(y_true, x).sum(), bounds=(0, 1), method='bounded')
preds = res.x
log_odds = np.log(preds / (1 - preds))
return log_odds
では先程のデータを使って精度を確認してみたいと思います。
今回は 0.1 ≦ γ ≦ 5.0 、0.1 ≦ α ≦ 1.0 の範囲で、それぞれ0.1刻みでパラメータを変動させてベストスコアを探索してみます。
import lightgbm as lgb
from scipy import optimize, special
# 簡易的なパラメータを定義
params = {'boosting_type': 'gbdt',
'verbose': -1,
'learning_rate': 0.01,
'objective': 'binary',
'metric': 'custom'
}
callbacks = []
callbacks.append(lgb.early_stopping(stopping_rounds=10, verbose=False))
# StratifiedKFold のインスタンスを生成
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=10)
# 探索する γ と α の範囲を定義
gamma = np.arange(0.1, 5.1, 0.1)
alpha = np.arange(0.1, 1.1, 0.1)
# ベストパラメータ、ベストスコアの変数を初期化
best_gamma = None
best_alpha = None
best_accuracy = None
# ベストパラメータの探索
for g in gamma:
for a in alpha:
accuracies = []
# Focal Lossのインスタンスを生成
fl = Focal_Loss(g, a)
for train_index, val_index in cv.split(X, y):
X_train, X_val = X.iloc[train_index], X.iloc[val_index]
y_train, y_val = y[train_index], y[val_index]
# 各データセットの init_score に初期化値を渡す
train_data = lgb.Dataset(X_train, y_train, init_score=np.full_like(y_train, fl.init_score(y_train), dtype=float))
val_data = lgb.Dataset(X_val, y_val, init_score=np.full_like(y_val, fl.init_score(y_train), dtype=float), reference=train_data)
valid_sets = [val_data]
# fobj と feval にそれぞれ対応するカスタム関数を渡す
model = lgb.train(params,
train_data,
num_boost_round=1000,
valid_sets=valid_sets,
fobj=fl.lgb_fobj,
feval=fl.lgb_feval,
callbacks=callbacks,
)
# シグモイド変換前に初期化値を追加した上で予測値を算出
y_pred = special.expit(fl.init_score(y_train) + model.predict(X_val))
# 確率が0.5を超える場合にラベルを1とし、そうでなければ0とする
y_pred = np.rint(y_pred)
accuracy = accuracy_score(y_val, y_pred)
accuracies.append(accuracy)
mean_accuracy = np.mean(accuracies)
# ベストスコア、ベストパラメータを更新
if isinstance(best_accuracy, type(None)):
best_accuracy = mean_accuracy
best_gamma = g
best_alpha = a
elif best_accuracy < mean_accuracy:
best_accuracy = mean_accuracy
best_gamma = g
best_alpha = a
else:
pass
# ベストスコア、ベストパラメータを出力
print(f'best_accuracy: {best_accuracy}, best_gamma: {best_gamma}, best_alpha: {best_alpha}')
best_accuracy: 0.7986666666666666, best_gamma: 0.1, best_alpha: 0.5
元々のAccuracyが 0.808 ぐらいだったので、Focal Lossを使うことでむしろ精度が落ちてしまっていますね。
ラベルの偏りが 3:1 というのが不均衡と呼ぶには足りなかったのでしょうし、他の要因もあるかもしれません。
いずれにしても、今回は使わない方が良さそうです。
(これを試したのはコンペ終了後なので、どのみち結果は確認できませんが)
LightGBMのハイパーパラメータチューニングである程度精度を改善できると思いますが、カスタム関数が関わるとちょっと複雑そうなので、今回はこれで終わりにしておきます。
次に参加するコンペで使う機会があれば試してみたいと思います。
9. 感想
実質の稼働時間が4日程度しかなく、熟考できなかったのが悔いの残るところです。
テストデータの予測をする際に StratifiedKFold で5分割の平均をとったデータを提出したかったのですが、時間がなく焦ってしまい train_test_split で妥協してしまいました。
特徴量エンジニアリングは全然上手くいかなかったので、まだまだ勉強不足であることを再確認でき、ある意味よかったのかもしれません。
またdocstringを英語表記してみましたが、こういったことにも慣れていきたいです。
目的は Intermediate の称号獲得なので、とりあえず最低ラインは突破しましたが、最終順位はやはり一位を狙いたかったです。
引き続き勉強を継続しつつ、最終的にメダルを狙っていきます。