はじめに
本記事は、Coursera Machine LearningコースのWeek10で学んだことをまとめています。機械学習を勉強したい人、機械学習を理解するためにCourseraに取り組んでいる人向けに書いています。
Coursera Machine Learning Week10を受講する前に
Week10の学習内容は特にWeek6の学習内容と関連があります。個人的にはWeek6の続きのように感じています。なので、Week6の学習内容を理解できていない人、Week6をまだ学習していない人はWeek6の学習を先にやることをおすすめします。
Coursera Machine Learning Week10 学習内容
Week10のタイトル「Large Scale Machine Learning」からもわかるとおり、大量のデータをどのように処理するかについて学習できます。
具体的には、以下の4つを学習できます。
- Stochastic Gradient Descent
- Mini-Batch Gradient Descent
- Online Learning
- Map Reduce and Data Parallelism
Stochastic Gradient DescentとMini-Batch Gradient DescentはWeek1で学習したGradient Descent(Batch Gradient Descent)を大量のデータを扱えるように改良したものです。
Online Learning と Map Reduce、Data Parallelismはデータを1度に全て処理するのではなく、1度に1つあるいは1部のデータを処理する考え方です。
では、それぞれについて説明します。
Stochastic Gradient Descent
Stochastic Gradient Descent(確率的最急降下法)は、1度に全てのデータからモデルを作るBatch Gradient Descentに対して、1度に1つのデータと既存のモデルから新しいモデルに更新するアルゴリズムです。
1度に1つのデータのみ使用するため、高速かつ連続して処理を行うことができます。ただし、使用するデータはランダムにシャッフルして選択する。
以下がStochastic Gradient Descentの目的関数とパラメータ${\theta}$更新の計算式です。
$$ J_{train}(\theta)=\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2 $$
$$ {\theta}_j := {\theta}_j - {\alpha} (h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)} $$
これまでに学習したBatch Gradient Descentの目的関数とパラメータ${\theta}$更新の計算式が次です。
$$ J_{train}(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2 $$
$$ {\theta}_j := {\theta}_j - {\alpha}\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})x_j^{(i)} $$
Stochastic Gradient DescentとBatch Gradient Descentと比較すると目的関数は同じですが、パラメータ${\theta}$の更新式が異なります。Stochastic Gradient Descentがパラメータの更新にデータを1つだけ使用しているのに対し、Batch Gradeient Descentはパラメータの更新に全てのデータを使用しています。
Stochastic Gradient Descentの目的関数収束チェック
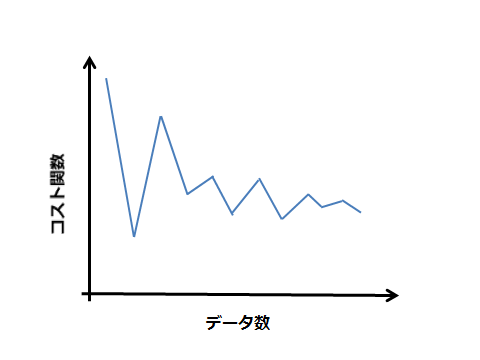
Stochastic Gradient Descentはデータ1つ毎にパラメータ${\theta}$を更新するため、常に目的関数が小さくなるとは限りません。そのため、目的関数が収束しているのかチェックする必要があります。
目的関数が収束しているかチェックするために、任意の回数分のコストの平均値をとり、チェックします。
(例)1000回毎にチェックする場合、1~1000回分の平均値、1001~2000回分の平均値、…(以下、同様)
以下のようになれば収束しているとみなせる。
収束していない場合もある
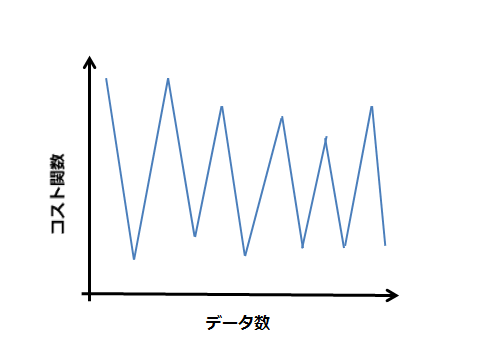
この場合、平均値をとる範囲を大きくすること(1000→10000)で以下の赤線のように改善できる。
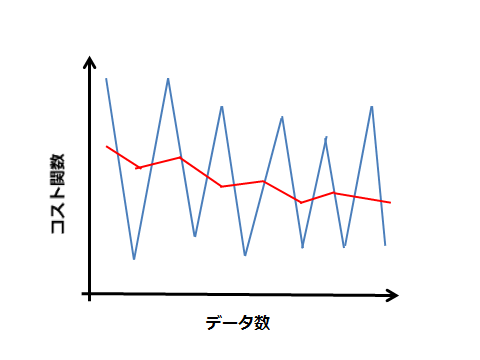
また、このグラフからもわかるように常に目的関数を最小化するわけではありません。すなわち、グローバル最小に近づいても、一致することはありません。グローバル最小近辺を行ったり来たりします。よりグローバル最小に近づくには、学習率${\alpha}$を小さく設定する必要があります。ただし、ゆっくり近づくようになります。
Mini-Batch Gradient Descent
次にMini-Batch Gradient Descentについて説明します。Mini-Batch Gradient Descentはをパラメータ${\theta}$の更新に全データの一部を使用します。
Mini-Batch Gradient Descentのパラメータ${\theta}$更新の計算式は以下のようになります。(目的関数はBatchGradient Descent、Stochastic Gradient Descentと同じなので省略します)
$$ {\theta}_j := {\theta}_j - {\alpha}\frac{1}{n}\sum_{k=i}^{i+n-1}(h_{\theta}(x^{(k)}) - y^{(k)})x_j^{(k)} $$
※nはパラメータ${\theta}$を1回更新するのに使用するデータ数
(例)全データが1000で、1度に10個のデータを使用してパラメータ${\theta}$を更新する場合
$$ {\theta}_j := {\theta}_j - {\alpha}\frac{1}{10}\sum_{k=i}^{i+9}(h_{\theta}(x^{(k)}) - y^{(k)})x_j^{(k)} $$
※全てのiについて行う(i=1,11,21,….991)
1度に扱うデータ数を増やすと、処理時間が長くなることから、動画では1度に扱うデータ数は2~100が良いと言われています。
扱うデータによってはStochastic Gradient Descentよりも高速な時があります。
Online Learning
Online Learning(オンライン学習)はデータを既存のモデルに新しいデータ1つを加えてモデルを更新し続けるアルゴリズムです。常にモデルを更新し続けるため、1度更新されたモデルを再度使うことはありません。また、モデルを更新するのにデータを1つだけ使用するのでBatch処理に比べて高速かつ低メモリで処理ができます。
Stochastic Gradient Descentはオンライン学習の1つの手法です。Gradient Descentだけでなく、Neural Network,Logistic Regression等、他の手法にもオンライン学習を適応できます。
Online Learningのメリット
Online Learningのメリットは常に新しいモデルで運用できることです。
常に、新しいモデルに更新することでより精度の高い学習が可能になります。特に、オンラインショッピングのレコメンド機能等、動的に変化するものを学習する場合にOnline Learningは有効だと考えられます。
Map Reduce and Data Parallelism
Map ReduceとData Parallelismとは、全てのデータを分割して処理し、最後に分割して処理したデータを結合する手法です。では、手順について説明します。
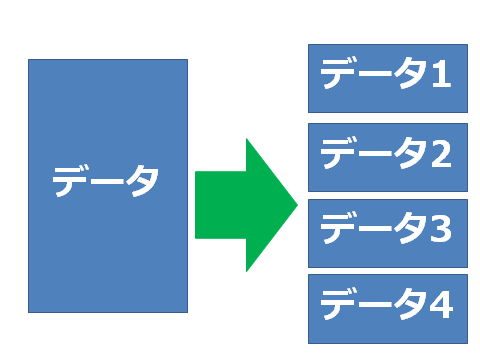
まず、データを分割します。
※4分割である必要はないです
次に、分割したデータ毎に仮説関数と観測値の誤差の2乗和を求めます。
例として、全データが400で4分割した場合を考えます。
上図で言えば、データ1が1番から100番のデータ、データ2に101番から200番、データ3に201~300番、データ4に301~400番データを分割したとします。データ1~4の仮説関数と観測値の誤差の2乗和をtemp1~4とすると、
$$ temp^{(1)} = \sum_{i=1}^{100}(h_{\theta}(x^{(i)})-y^{(i)})^2x_j^{(i)} $$
$$ temp^{(2)} = \sum_{i=101}^{200}(h_{\theta}(x^{(i)})-y^{(i)})^2x_j^{(i)} $$
$$ temp^{(3)} = \sum_{i=201}^{300}(h_{\theta}(x^{(i)})-y^{(i)})^2x_j^{(i)} $$
$$ temp^{(4)} = \sum_{i=301}^{400}(h_{\theta}(x^{(i)})-y^{(i)})^2x_j^{(i)} $$
になります。
最後に、各tempを結合してパラメータ${\theta}$を更新します。更新式は以下のようになります。
$$ {\theta}_j := {\theta}_j - {\alpha}\frac{1}{400}(temp_j^{(1)}+temp_j^{(2)} + temp_j^{(3)} +temp_j^{(4)}) $$
以上がMap Reduce and Data Parallelismの考え方です。
最後に
本記事では機械学習を行う上で、大量のデータをどのように扱うかについて書いてきました。この記事が機械学習を学びたい人の助けになれば幸いです。