Class activation mappingを用いたCNNの可視化

概要

Global average poolingをCNNに用いることでclass activation mapの生成を行った。
Cifar-10を学習データとして生成されたマップから、CNNが画像内のカテゴリーを特定している様子を確認した。

はじめに

従来のCNNは畳み込み層の出力を最終的にベクトル化し、全結合層に渡してソフトマックス層で分類を行っている。
しかしながら、この方法では畳み込み層で生成されたマップ間の情報が分類において不明瞭になることや大量のパラメータを要することで過学習になることなどの課題がある。

Global average pooling(GAP)[1]は最後の畳み込み層で得られた各々のマップ(各カーネル)に対してaverage poolingを実行する方法である。
ここで得られたデータ(ベクトル化されている)をソフトマックス層に渡して分類を行う。

具体的な手順を以下に示す。

$f_k(i,j)$をカーネル$k$番目、座標$(i,j)$におけるピクセルとする。GAPから得られる$k$番目のカーネルが取る値$F_k$は
$$\begin{eqnarray}
F_k = \frac{1}{Z} \sum_{i,j} f_k(i,j)
\end{eqnarray}$$
となる。ただし、$Z$は各マップが持つピクセル数。続いて、ソフトマックス層のクラス$c$のユニットに渡す値$S_c$は
$$\begin{eqnarray}
S_c = \sum_k w_k^c F_k
\end{eqnarray}$$
で与えられる。ただし、$w_k^c$はクラス$c$に対する$F_k$またはカーネル$k$のマップそのものの重み(重要度)を表す。

従って、class activation map(CAM)[2]は$w_k^c$を掛けた$f_k(i,j)$の線形結合で与えられる。
ある入力画像のクラス$c$に対するactivation map $M_c$は
$$\begin{eqnarray}
M_c(x,y) = \sum_k w_k^c f_k(x,y)
\end{eqnarray}$$
で与えられる。

セットアップ

CPUでも学習できる程度の比較的シンプルなCNNモデルを構築しました。今回用いたモデルおよびコードの一部を以下に載せます。Tensorflowで記述しています。
通常のCNNで用いるpoolingにはmax pooling、活性化関数はReLUを使用しました。GlobalAvgPoolingで用いている関数は通常のpoolingと同じでtf.nn.avg_poolを使用しています。パラメータの更新手法としてAdamを用いました。

layers = [                            # (height)x(width)x(kernel)
    Conv((3, 3, 3, 32), tf.nn.relu, padding='SAME'),  # 32x32x3 -> 32x32x32
    Conv((3, 3, 32, 32), tf.nn.relu, padding='SAME'),  # 32x32x32 -> 32x32x32
    Pooling((1, 2, 2, 1)),            # 32x32x32 -> 16x16x32
    Conv((3, 3, 32, 128), tf.nn.relu, padding='SAME'), # 16x16x32 ->  16x16x128
    Conv((3, 3, 128, 128), tf.nn.relu, padding='SAME'), # 16x16x128 ->  16x16x128
    Conv((3, 3, 128, 128), tf.nn.relu, padding='SAME'), # 16x16x128 ->  16x16x128
    GlobalAvgPooling((1, 16, 16, 1)),            #  16x16x128 ->  1x1x128
    Flatten(),
    Dense(128, 10, tf.nn.softmax)
]

x = tf.placeholder(tf.float32, [None, 32, 32, 3])
t = tf.placeholder(tf.float32, [None, 10])

def f_props(layers, x):
    for layer in layers:
        x = layer.f_prop(x)
    return x

y = f_props(layers, x)

cost = -tf.reduce_mean(tf.reduce_sum(t * tf.log(tf.clip_by_value(y, 1e-10, 1.0)), axis=1))
train = tf.train.AdamOptimizer(0.001).minimize(cost)

valid = tf.argmax(y, 1)

以下のコードでは入力した画像xについての10クラス分のCAM(cmap)を畳み込みの最終層の出力convとソフトマックス層の重みwから計算しています。
tf.einsumはEinstein summation(アインシュタインの縮約記法)であり、tf.mutmalやnp.dotの一般化(テンソル型への拡張)です。

def get_cmap(layers, x):
    n_layers = 0
    for layer in layers:
        if n_layers == 5:
            conv = layer.f_prop(x)
            x = layer.f_prop(x)
        else:
            x = layer.f_prop(x)
        n_layers += 1
    w = layers[-1].W
    conv_reshape = tf.reshape(conv, [-1, 16*16, 128]) #16x16x128
    cmap = tf.einsum('ijk,kl->ijl', conv_reshape, w)
    cmap = tf.reshape(tf.transpose(cmap, [0, 2, 1]), [-1, 10, 16, 16])
    conv = tf.reshape(tf.transpose(conv, [0, 3, 1, 2]), [-1, 128, 16, 16])
    return cmap, conv, w

localizer = get_cmap(layers, x)

入力の画像とCAMのサイズをあわせるために得られたCAMに対して以下の処理をしました。

import scipy.ndimage
cam_re = scipy.ndimage.zoom(cmap, (1,1,2,2), order=1)

Cifar10のデータセットを用いて学習を行いました。ただし、学習データのflipおよびcrop処理した画像も含めることでデータの水増しをしました。

結果

15エポック学習をさせました。コスト関数およびF1スコアの結果を下図に示します。

Cifar10には次の10クラスが含まれています。
airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck

幾つかのクラスについて正しく分類できたデータの元画像とCAMを以下に示します。

• 犬

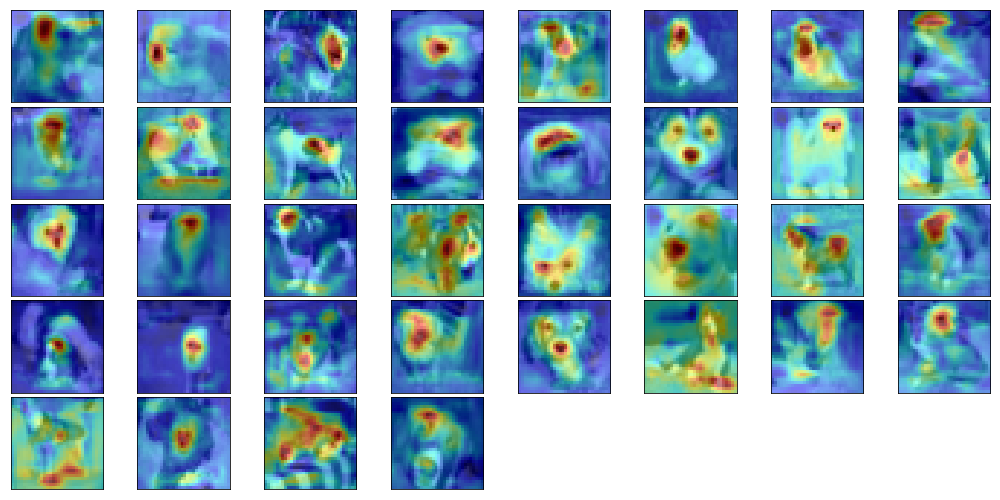
• 猫

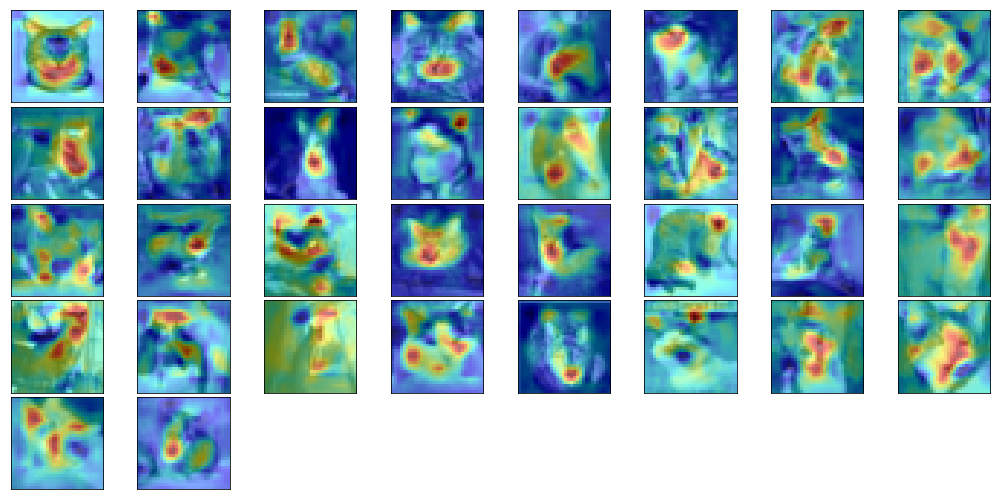
• カエル

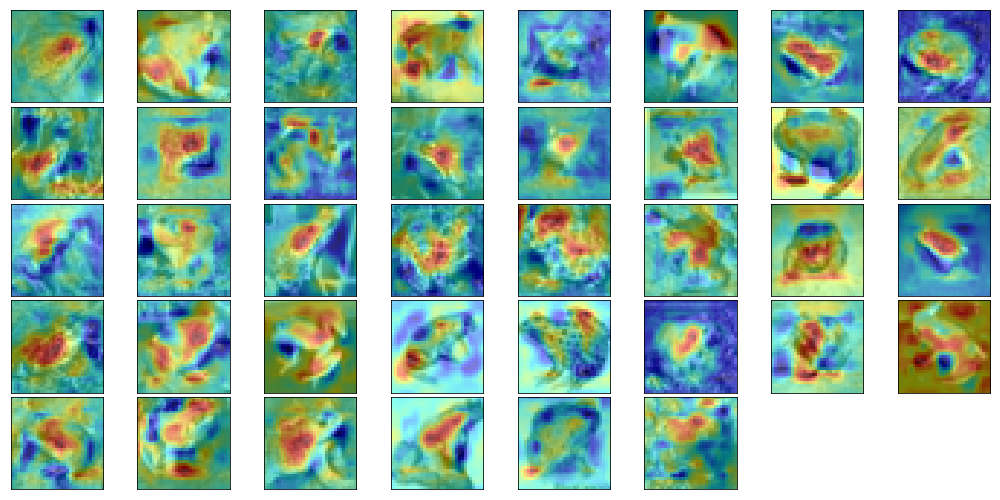
• 車

メモ

文献[2]ではCAMを用いたモデルでは分類の精度が向上しないという点が課題としてあげられていました。また、既存のモデル(VGGnetやAlexNet)をそのまま使うことができないなどの問題もあります。こうした問題を解決する方法としてGrad-CAM[3]などがあります。

参考文献

[1] M. Lin et al. Network in network
[2] B. Zhou et al. Learning deep features for disctiminative localization
[3] R. Selvaraju et al. Grad-CAM: visual explanations from deep networks via gradient-based localization