概要
経済学部の授業で常に安定性を満たすDAアルゴリズムについて学習しました。DAアルゴリズムは常に安定性を満たすアルゴリズムでマーケットデザインにおいて重要な役割を担っています。授業ではコードについて教わらなかったため、経済学とPythonの勉強として、DAマッチングを実現するシステムをpythonを用いて自力で作成してみました。
DAマッチングの詳しい説明はこちらの記事がわかりやすかったです↓
https://miiitomi.github.io/p/matching/
Pythonコード
決して綺麗なコードとは言えません！
ここではプレイヤー集合1（労働者）がプレイヤー集合2（企業）に提案するアルゴリズムを考えます。
プレイヤー集合の集合は辞書型で与えられるとします。
例えば、企業の選好が
{"c1":["w3","w2","w1"], "c2":["w1","w2","w3"]}
となるとき、企業c1はw3,w2,w1の順に好み、c2はw1,w2,w3の順で好むとします。
また
{"c1":["w3","w2","w1"], "c2":["w1"]}
となるとき、c2はw2,w3と組むなら誰とも組まない方がマシだと考えることとします。
以上をもとに、DAアルゴリズムを実装してみます。
import copy
class DAalgorism:
def __init__(self, preference_dict1, preference_dict2):
self.set_values(preference_dict1, preference_dict2)
def set_values(self, preference_dict1, preference_dict2):
"""
初期値を設定する。プレイヤー集合1提案型DAアルゴリズムを考える。
"""
self.player1 = preference_dict1 #提案可能なプレイヤー集合1の選好を示す辞書
self.player2 = preference_dict2 #受入可能なプレイヤー集合2の選好を示す辞書
self.player1_to_reffer = self.player1.copy() #参照用
self.player1_count = {k:0 for k in list(self.player1.keys())} #提案回数
self._proposals_dict = {k:[] for k in list(self.player2.keys())} #提案
def apply_game(self, player_name, i=0):
"""
player_nameがi番目の選好に応募する。
i番目の選好が存在しない場合、何もしない。
"""
if i < len(self.player1[player_name]):
preference = self.player1[player_name][i]
self._proposals_dict[preference].append(player_name)
def is_over_capacity(self, keep_list, q):
return len(keep_list) > q
def remove_least_preferred_player(self, preference_list2, keep_list2):
"""
選好の低いプレイヤーを1人取り除く。
"""
for player1 in preference_list2[::-1]:
if player1 in keep_list2:
keep_list2.remove(player1)
return keep_list2, player1 #取り除いた後の選好と、プレイヤーを返す。
def choose_player(self, player_name, q):
"""
プレイヤー2が選好をもとにプレイヤー1を選ぶ。
"""
preference_list2 = self.player2[player_name]
keep_list2 = self._proposals_dict[player_name]
exile_list = []
while True:
if self.is_over_capacity(keep_list2, q):
rlpp = self.remove_least_preferred_player(preference_list2, keep_list2)
keep_list2 = rlpp[0]
exile_list.append(rlpp[1])
else:
break
self._proposals_dict[player_name] = keep_list2
return exile_list
def filter_players(self, keys_to_keep):
"""
プレイヤー集合1の辞書から現時点でマッチングしていない人を厳選
"""
referance_list = self.player1_to_reffer
new_dict = {key: referance_list[key] for key in keys_to_keep if key in referance_list}
return new_dict
def do_step(self, q):
# プレイヤー1が選考をもとにプレイヤー2に応募する。
for player1 in list(self.player1.keys()):
count = self.player1_count[player1]
self.apply_game(player1,count)
# プレイヤー2は選考をもとにプレイヤー1を厳選する。
exiled_list = []
for player2 in list(self.player2.keys()):
exiled_players = self.choose_player(player2,q)
if exiled_players != None:
for ep in exiled_players:
self.player1_count[ep] += 1
exiled_list.extend(exiled_players)
# 提案可能なプレイヤーを更新する。
self.player1 = self.filter_players(exiled_list)
def propose_combination(self,q=1):
# 提案可能なプレイヤーがいなくなるまで繰り返す。
while len(self.player1) > 0:
self.do_step(q)
return self._proposals_dict
def exchange_players(self,q=1):
"""
プレイヤー集合2提案型DAメカニズムに変更する。
"""
self.player1 = self.player2.copy()
self.player2 = self.player1_to_reffer.copy()
self.player1_to_reffer = self.player1.copy()
self.player1_count = {k:0 for k in list(self.player1.keys())}
self._proposals_dict = {k:[] for k in list(self.player2.keys())}
return self.propose_combination(q)
具体的な状況を当てはめて考えてみます。
労働者の選好が
{"w1":["c1","c2"], "w2":["c2"], "w3":["c2","c1"]}
のように表されるとします。w2はc1と組むなら誰ともマッチングしない方がいいと考えているようです。
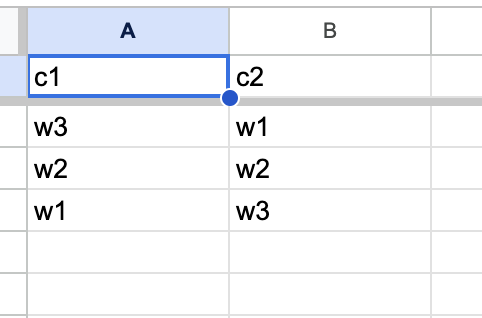
一方で企業の選好が、
{"c1":["w3","w2","w1"], "c2":["w1","w2","w3"]}
のように表されるとします。
ここで労働者提案型DAアルゴリズムのときには企業は労働者を2名まで受け入れ、企業提案型DAアルゴリズムの時には労働者は学校を2校まで受入れるとします。
以上に基づき、労働者提案型DAメカニズムと企業提案型マッチングをそれぞれ行うとします。
if __name__=="__main__":
dict1 = {"w1":["c1","c2"], "w2":["c2"], "w3":["c2","c1"]}
dict2 = {"c1":["w3","w2","w1"], "c2":["w1","w2","w3"]}
da = DAalgorism(dict1,dict2)
p1 = da.propose_combination(q=2)
print("プレイヤー1提案型DAマッチング：")
print(p1)
# もし提案するプレイヤー集合を変更したいなら
p2 = da.exchange_players(q=2)
print("プレイヤー2提案型DAマッチング：")
print(p2)
結果はこのようになりました。
プレイヤー1提案型DAマッチング
{'c1': ['w1'], 'c2': ['w2', 'w3']}
プレイヤー2提案型DAマッチング：
{'w1': ['c2'], 'w2': [], 'w3': ['c1']}
労働者提案型の時はc1とw1がマッチングし、c2とw2,w3がマッチングしました。
また企業提案型の時はw1とc2が、w3とc1がマッチングし、w2は誰ともマッチングしません。
こちらのコードはGithubにも上げておきました。
https://github.com/KANEI/DAalgorism/tree/main
より実践的なことをしてみる
ChatGPTに「このpythonのコードをGASで書き換えて」というと簡単に書いてくれました。
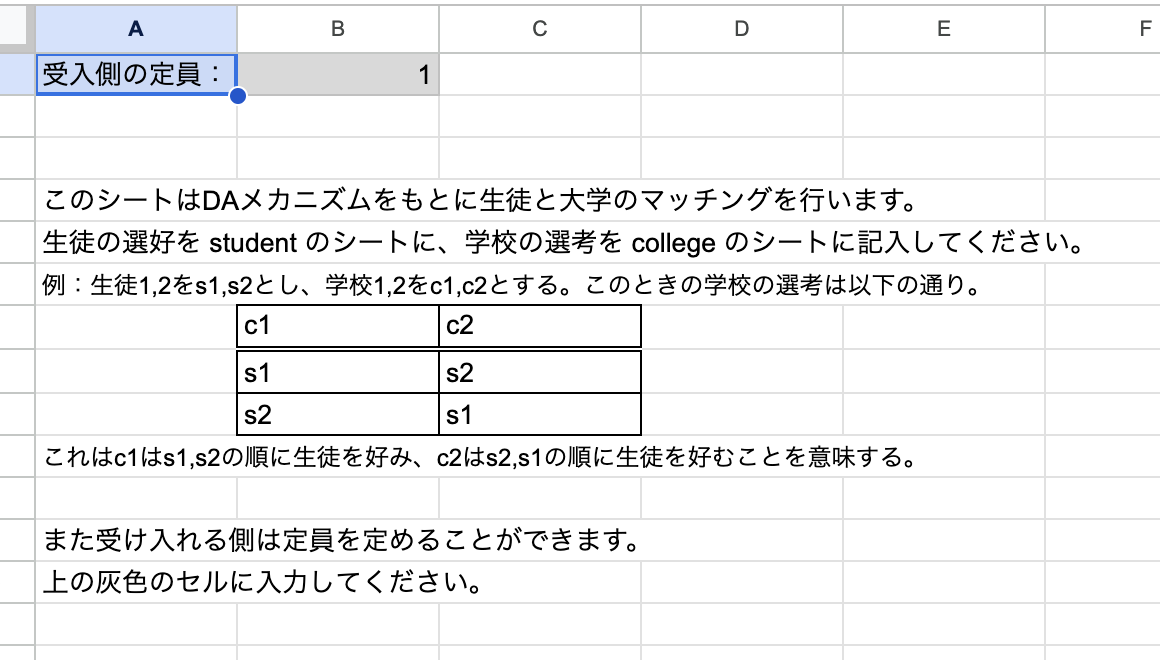
そのコードを微調整して、Google Spreadsheetに選考を入力してくれると自動的に安定マッチングを行ってくれるシステムをGoogle Apps Scriptで作成しました。
システムの概要
（今度は学校と生徒のマッチングを考えます。）
studentのシートに先ほどの労働者の選好を入れます。
collegeのシートに先ほどの企業の選考を入れます。
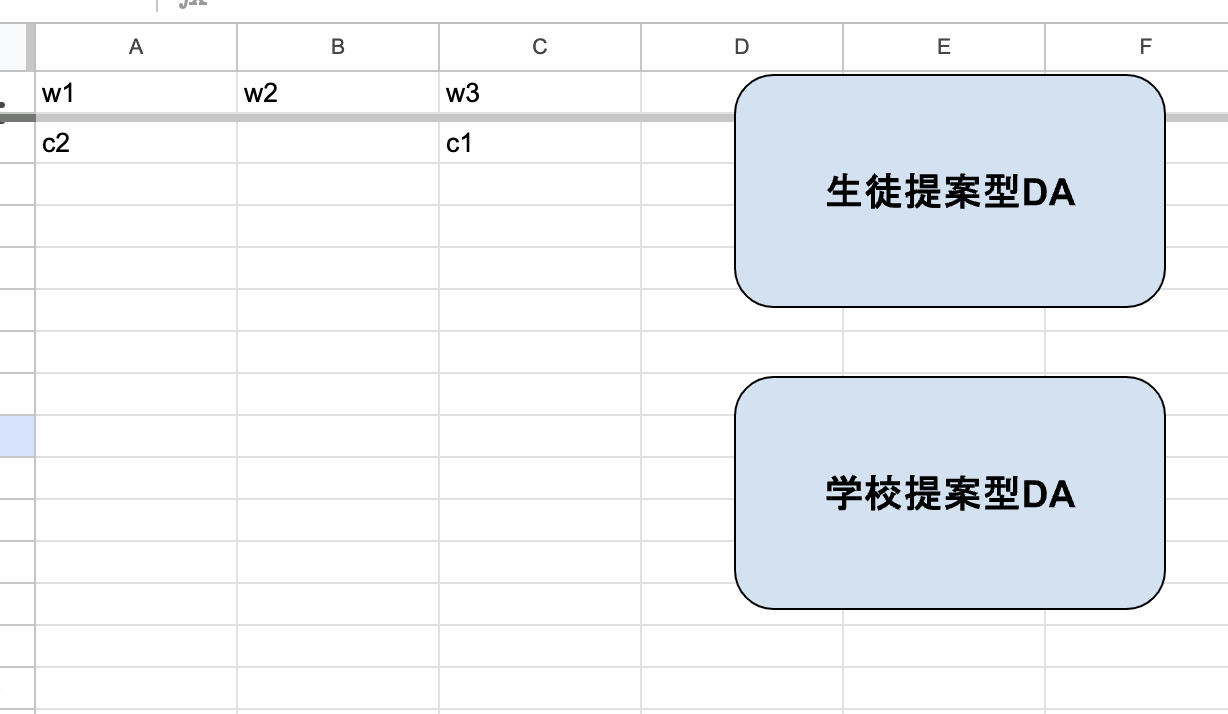
定員の数を2に設定して、生徒提案型DAのボタンを押すと次の結果を出力します。
対して、学校提案型DAのボタンを押すと次の結果を出力します。
労働者提案型の時はc1とw1がマッチングし、c2とw2,w3がマッチングしました。
また企業提案型の時はw1とc2が、w3とc1がマッチングし、w2は誰ともマッチングしません。
これは上記のpythonの値と一致します！
GASのコード
class DAalgorism {
constructor(preferenceDict1, preferenceDict2) {
this.setValues(preferenceDict1, preferenceDict2);
}
setValues(preferenceDict1, preferenceDict2) {
this.player1 = JSON.parse(JSON.stringify(preferenceDict1));
this.player2 = JSON.parse(JSON.stringify(preferenceDict2));
this.player1ToRefer = JSON.parse(JSON.stringify(this.player1));
this.player1Count = {};
for (const key of Object.keys(this.player1)) {
this.player1Count[key] = 0;
}
this.proposalsDict = {};
for (const key of Object.keys(this.player2)) {
this.proposalsDict[key] = [];
}
}
applyGame(playerName, i = 0) {
if (!(playerName in this.player1) || !Array.isArray(this.player1[playerName])) return;
if (i < this.player1[playerName].length) {
const preference = this.player1[playerName][i];
if (preference in this.proposalsDict) {
this.proposalsDict[preference].push(playerName);
}
}
}
isOverCapacity(keepList, q) {
return keepList.length > q;
}
removeLeastPreferredPlayer(preferenceList2, keepList2) {
for (let i = preferenceList2.length - 1; i >= 0; i--) {
const player = preferenceList2[i];
if (keepList2.includes(player)) {
const index = keepList2.indexOf(player);
keepList2.splice(index, 1);
return [keepList2, player];
}
}
return [keepList2, null];
}
choosePlayer(playerName, q) {
if (!(playerName in this.player2) || !(playerName in this.proposalsDict)) return [];
const preferenceList2 = this.player2[playerName];
let keepList2 = [...this.proposalsDict[playerName]];
const exileList = [];
while (this.isOverCapacity(keepList2, q)) {
const [newList, exiled] = this.removeLeastPreferredPlayer(preferenceList2, keepList2);
keepList2 = newList;
if (exiled !== null) exileList.push(exiled);
}
this.proposalsDict[playerName] = keepList2;
return exileList;
}
filterPlayers(keysToKeep) {
const newDict = {};
for (const key of keysToKeep) {
if (this.player1ToRefer[key]) {
newDict[key] = this.player1ToRefer[key];
}
}
return newDict;
}
doStep(q) {
for (const player of Object.keys(this.player1)) {
if (player in this.player1Count) {
const count = this.player1Count[player];
this.applyGame(player, count);
}
}
let exiledList = [];
for (const player of Object.keys(this.player2)) {
const exiledPlayers = this.choosePlayer(player, q);
if (exiledPlayers.length > 0) {
for (const ep of exiledPlayers) {
if (ep in this.player1Count) {
this.player1Count[ep]++;
}
}
exiledList = exiledList.concat(exiledPlayers);
}
}
this.player1 = this.filterPlayers(exiledList);
}
proposeCombination(q) {
while (Object.keys(this.player1).length > 0) {
this.doStep(q);
}
return this.proposalsDict;
}
}
function getSheetDataAsDictionary(sheetname) {
// スプレッドシートの取得（"sheetname" という名前のシート）
var sheet = SpreadsheetApp.getActiveSpreadsheet().getSheetByName(sheetname);
// データの取得（最初の行をヘッダー、残りをデータとして取得）
var data = sheet.getDataRange().getValues();
// ヘッダー行を取り出す（最初の行）
var headers = data[0];
// 辞書型でデータを格納（キーは列名、値はリスト）
var result = {};
// ヘッダーごとにリストを作成
for (var j = 0; j < headers.length; j++) {
result[headers[j]] = [];
}
// データ行をリストに追加
for (var i = 1; i < data.length; i++) {
for (var j = 0; j < headers.length; j++) {
result[headers[j]].push(data[i][j]);
}
}
return result;
}
function get_p(){
var sheet = SpreadsheetApp.getActiveSpreadsheet().getSheetByName("README");
// 入力されたqを取得
q = sheet.getRange('B1').getValue()
return Number(q)
}
function outputDictionaryAsTable(data) {
var sheet = SpreadsheetApp.getActiveSpreadsheet().getSheetByName("output");
// データ範囲を取得して、値を削除
sheet.clearContents();
// ヘッダー行を取得（辞書のキー）
var headers = Object.keys(data);
// 最初の行にヘッダーを設定
sheet.getRange(1, 1, 1, headers.length).setValues([headers]);
// 各列の最大データ長を取得
var numRows = Math.max(...headers.map(key => Array.isArray(data[key]) ? data[key].length : 0));
var rows = [];
for (var i = 0; i < numRows; i++) {
var row = [];
for (var j = 0; j < headers.length; j++) {
var key = headers[j];
row.push((Array.isArray(data[key]) && i < data[key].length) ? data[key][i] : ""); // 存在しない部分には空文字
}
rows.push(row);
}
// 2行目以降にデータを設定
if (rows.length > 0) {
sheet.getRange(2, 1, rows.length, headers.length).setValues(rows);
}
Logger.log("データの出力が完了しました！");
}
// 実行例
function student_proposal() {
const dict1 = getSheetDataAsDictionary("student");
const dict2 = getSheetDataAsDictionary("college")
const q = get_p()
const da = new DAalgorism(dict1, dict2);
const p1 = da.proposeCombination(q);
Logger.log("Result 1: " + JSON.stringify(p1));
outputDictionaryAsTable(p1)
}
function college_proposal(){
const dict1 = getSheetDataAsDictionary("college");
const dict2 = getSheetDataAsDictionary("student")
const q = get_p()
const da = new DAalgorism(dict1, dict2);
const p2 = da.proposeCombination(q);
Logger.log("Result 2: " + JSON.stringify(p2));
outputDictionaryAsTable(p2)
}
ChatGPTには大変お世話になりました...!
振り返り
DAアルゴリズムはGale-Shapleyアルゴリズムとも呼ばれるらしく、そちらの方はコードの数が結構ありました。
特にわかりやすかったのが、こちらの記事です。
https://builtin.com/articles/gale-shapley-algorithm
男女のマッチングとして単純化しているもののコードが綺麗でとても参考になりました。
実践的な経済学であるマーケットデザイン・メカニカルデザインにさらに興味を持ちました！