はじめに
相関係数は統計学において、2つの変数間の線形関係の強さと方向を示す重要な指標です。
多くの人が「相関係数は-1から1の間に収まる」ということは聞いたことがあるかもしれませんが、なぜその範囲に限定されるのかは理解してる人は少ないと思います。
そこで、本記事では、まず、相関係数の基本的な定義と意味を簡単に説明し、
その後、数学的な裏付けとしてコーシー・シュワルツの不等式を用いて、なぜ相関係数がこの範囲に収まるかを証明しようと思います。
私は数学に関して、完璧に理解してるわけではないので、
厳密には違うなどあればコメントをお願いします。。。
相関係数とは?
相関係数とは、2つの変数の間にどれだけ強い線形関係があるかを示す指標です。最も一般的な相関係数はピアソンの積率相関係数で、以下の式で定義されます
$$
r = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}}
$$
この式は、2つの変数の共分散を、それぞれの標準偏差の積で割ったものです。
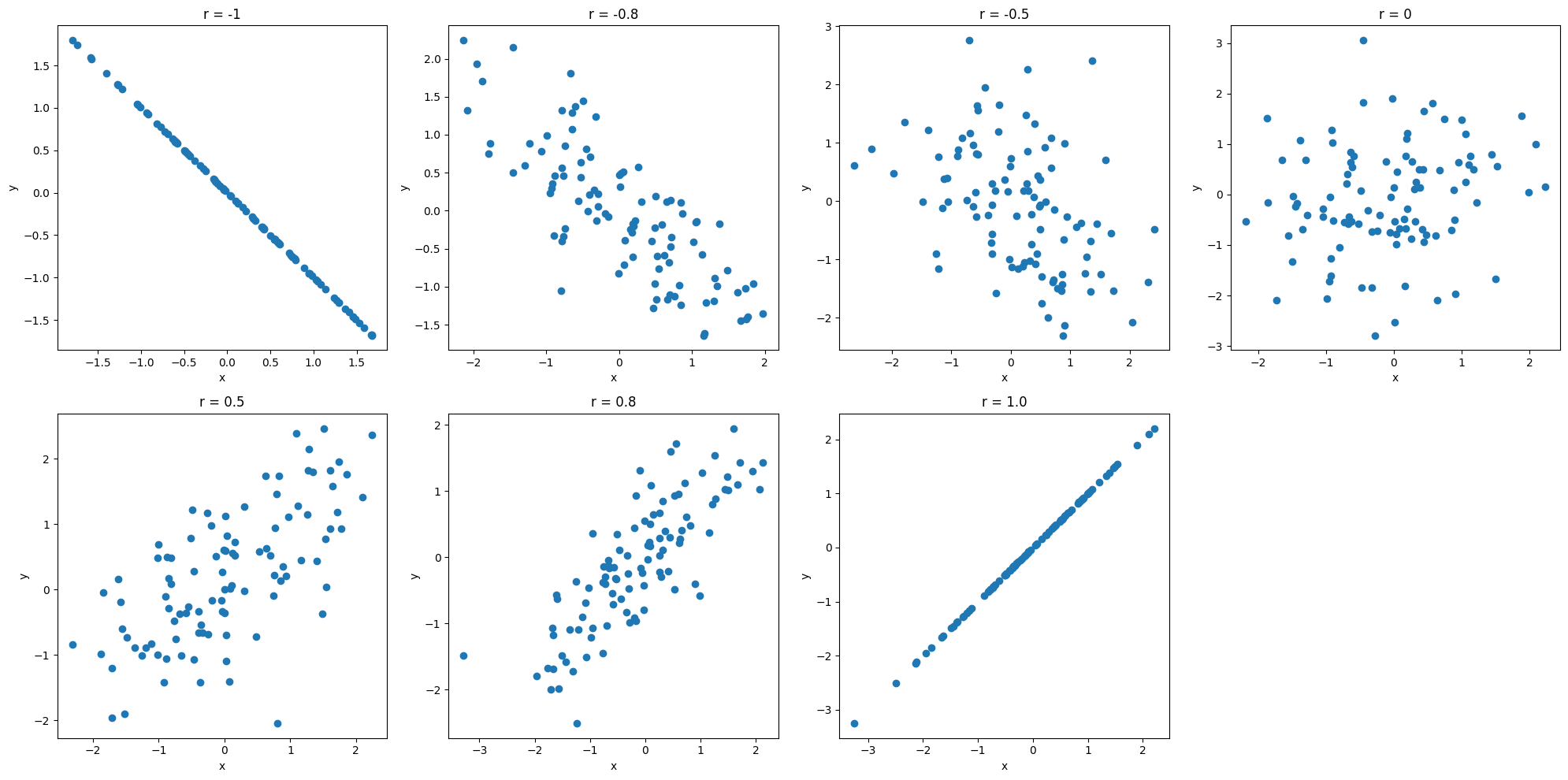
$r$の値によって以下のように読み取れることが変わってきます
- $r$が1に近い時ときは正の相関が強い
- $r$が-1に近い時ときは負の相関が強い
- $r$が0に近い時ときは相関関係が薄い
では、なぜこの値が必ず -1 から 1 の間に収まるのでしょうか?
-1から1までになる証明
この範囲に収まる理由は、コーシー・シュワルツの不等式にあります。これは線形代数や解析学で非常に重要な不等式で、次のように表されます
$$
\left( \sum_{i=1}^{n} a_i b_i \right)^2 \leq \left( \sum_{i=1}^{n} a_i^2 \right) \left( \sum_{i=1}^{n} b_i^2 \right)
$$
$a_i, b_i$は任意の実数列
証明や詳しい説明については以下が参考になります
コーシーシュワルツの不等式とそのエレガントな証明
相関係数の書き換え
では証明します
まず、コーシー・シュワルツの不等式を用いるために相関係数を
$a_i = x_i - \bar{x} \quad b_i = y_i - \bar{y}$で置き換えて,以下のように書き換えます
$$
r = \frac{\sum_{i=1}^{n} a_i b_i}{\sqrt{\sum_{i=1}^{n} a_i^2} \cdot \sqrt{\sum_{i=1}^{n} b_i^2}}
$$
コーシー・シュワルツの不等式を使った証明
コーシー・シュワルツの式を変形します
$$
\left( \sum_{i=1}^{n} a_i b_i \right)^2 \leq \left( \sum_{i=1}^{n} a_i^2 \right) \left( \sum_{i=1}^{n} b_i^2 \right)
$$
両辺の平方根を取ると
$$
\left| \sum_{i=1}^{n} a_i b_i \right| \leq \sqrt{\sum_{i=1}^{n} a_i^2} \cdot \sqrt{\sum_{i=1}^{n} b_i^2}
$$
この不等式の両辺を$ ( \sqrt{\sum a_i^2} \cdot \sqrt{\sum b_i^2} )$ で割ると
$$
\left| \frac{\sum_{i=1}^{n} a_i b_i}{\sqrt{\sum_{i=1}^{n} a_i^2} \cdot \sqrt{\sum_{i=1}^{n} b_i^2}} \right| \leq 1
$$
相関係数の書き換えで、出てきた式の形になりました。
よって、
$$
|r| \leq 1
$$
となり、相関係数は-1から1までなのがわかりました。
なぜ成り立つのかを考えるのは重要なので、今後も様々な式の成り立ちを考えてアウトプットしていこうと思います。